Un sitio personal para aprender desarrollo web
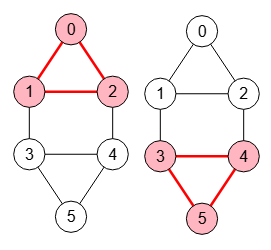
Un clique en un grafo es un subconjunto de nodos tal que cada par de nodos está conectado. El tamaño de un clique es su número de nodos. Los de tamaño 1 son los propios nodos y los de tamaño 2 las aristas. Para obtenerlos buscamos todos los subgrafos inducidos que sean completos.
Además podemos buscar los cliques máximos y cliques maximales. Así como los anticliques que son conjuntos independientes de vértices no conectados. De igual forma buscamos todos los anticliques, los máximos y los maximales.

Implementamos en Grafos SVG algoritmos para obtener subgrafos, que son subconjuntos de nodos y aristas. En un grafo con n nodos definimos un subgrafo inducido al grafo resultante compuesto con k ≤ n nodos y todas sus aristas incidentes. Y de forma general definimos un subgrafo a un inducido tras lo cual eliminamos cero o más aristas. Mientras que un subgrafo recubridor al que contiene todos los n nodos y sólo algunas aristas del grafo original.
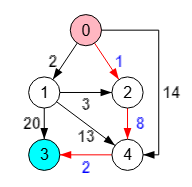
Encontrar los caminos mínimos en un grafo dirigido supone definir un nodo raíz y buscar los caminos al resto de nodos con suma de longitudes mínima. En principio se define para grafos dirigidos, pero luego veremos que también puede aplicarse a no dirigidos. Es imprescindible que las longitudes de las aristas no sean negativas. Se resuelve con los algoritmos de Dijkstra y Floyd.
Ya traté este problema en el año 2020 en el tema algoritmo de Dijkstra con ocasión de exponer un ejemplo de aplicación de algoritmos voraces y también en el algoritmo de Floyd para exponer un ejemplo de aplicación de programación dinámica. Ahora los incorporo en la aplicación Grafos SVG con algunas mejoras en la presentación y trazado.
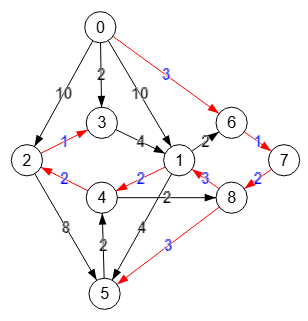
Vimos en el tema anterior los árboles de recubrimiento mínimo (MST Minimum Spanning Tree) con los algoritmos de Prim y Kruskal, árboles que sólo aplicaban a grafos no dirigidos. Para grafos dirigidos hablamos de arborescencia, que es un grafo dirigido con un nodo raíz donde desde esa raíz al resto de cada uno de los nodos sólo hay un único camino posible. Digamos que hablamos de árboles para no dirigidos y arborescencias con una raíz para dirigidos, pero en el fondo ambos son árboles. Si con árboles no dirigidos hablábamos de MST, para dirigidos a veces se les denomina DMST Directed Minimum Spanning Tree. Buscar una arborescencia de mínimo coste en un grafo dirigido supone encontrar aquella cuya suma de pesos sea mínima.
En la aplicación Grafos SVG implementamos dos nuevos algoritmos. El primero es un algoritmo voraz para encontrar una arborescencia de mínimo coste sin especificar ningún nodo raíz. Como todos los voraces, no siempre consigue la solución óptima. Dispone de una opción para encontrar la raíz con mínimo coste, aplicando un segundo algoritmo que es una implementación del algoritmo de Edmonds, que siempre consigue la arborescencia de mínimo coste.
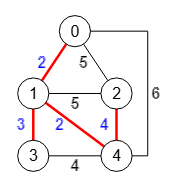
El árbol de recubrimiento mínimo (o MST de Minimum Spanning Tree) en un grafo conexo no dirigido es un subgrafo que conecta todos los nodos y cuyo coste de la suma del valor de las aristas es mínimo.
En el año 2020 expuse unos temas relacionados con los algoritmos voraces. Una aplicación de esos algoritmos se exponía en el tema sobre árboles de recubrimiento mínimo, con el algoritmo de Prim y el algoritmo de Kruskal, algoritmos que ahora adaptamos para integrar en la aplicación de Grafos SVG.
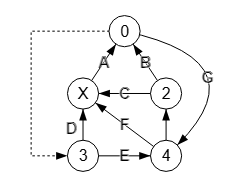
He modificado el tema Componentes conectados desagrupando algunos apartados para trasladarlos al nuevo tema Componentes conectados 2, pues necesitaba incorporar nuevos algoritmos y el documento empezaba a ser bastante extenso. Agrego en el primer tema un apartado para explicar el algoritmo convertir a fuertemente conectado convertToStronglyConnected() para convertir un grafo dirigido a fuertemente conectado.
Y también es el grafo una arborescencia isGraphArborescence() para saber sin un grafo dirigido es una arborescencia, que se define para un nodo raíz de tal forma que entre esa raíz y el resto de cada uno de los nodos sólo existe un único camino posible.

En el tema que explicamos la estructura JSON que usa la aplicación Grafos SVG vimos como importar y exportar entre JSON y otras estructuras como matriz de adyacencia, lista de aristas, lista de adyacencias, matriz de incidencia y matriz de distancias. En esa gestión interviene la estructura JSON.
Ahora alternativamente implementamos algoritmos para convertir entre la matriz de adyacencia y esas otras estructuras, sin intervenir el JSON. Con convertToAdjacencyMatrix() que ya tenía implementado para convertir a matriz de adyacencia desde una lista de aristas, lista de adyacencias, matriz de incidencias o matriz de distancias. Y con getEdges() también implementado para obtener la lista de aristas desde una matriz de adyacencia.
Y los nuevos algoritmos getAdjacencies() para obtener la lista de adyacencias, getIncidences() para obtener la matriz de incidencias y getDistances() para obtener la matriz de distancias, todos a partir de una matriz de adyacencia.
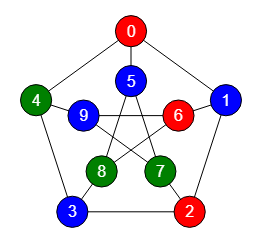
El coloreado de grafos, o más exactamente el coloreado de los nodos de un grafo, consiste en dotar de colores a los nodos de forma que nodos adyacentes no compartan el mismo color. Puede contemplarse también de igual forma el coloreado de aristas tal que que todas las aristas que comparten un nodo tengan colores diferentes. En todos los casos para grafos dirigidos se ignoran la direcciones de las aristas coloreándose como si fuera no dirigido.
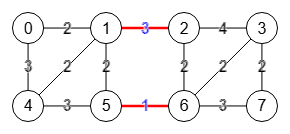
Encontrar un corte mínimo de aristas con el algoritmo de Stoer-Wagner en un grafo conectado y no dirigido con n nodos conlleva iterar n-1 veces identificando un corte en cada paso y almacenar el mínimo encontrado que, al final, será el mínimo del grafo.
Se selecciona el nodo a=1 que se mantiene fijo en todos los pasos. En cada paso creamos un conjunto de vértices con ese nodo A=[1] y vamos agregando vértices restantes en el orden de los más fuertemente conectados con los vértices de A, quedando al final de esa lista los nodos "s" y "t", siendo "t" el menos fuertemente conectado. Esto nos permite obtener un corte parcial de "t" con respecto al resto con un cierto peso entre ambos componentes. Iremos almacenando siempre el menor de todos los cortes parciales que nos servirá al final para obtener el corte mínimo del grafo. En cada paso contraemos los nodos "t" y "s" y el grafo contraído servirá de base para el siguiente paso. Cuando lleguemos al paso n-1 el grafo contraído tendra 2 nodos y habremos finalizado estos pasos, tras lo cual recuperamos el corte mínimo almacenado que será el que se devuelva.
El algoritmo de Karger es un procedimiento probabilista para encontrar el corte mínimo de aristas de un grafo no dirigido y conectado. Un algoritmo es probabilista si en el resultado intervienen decisiones que se toman al azar. A diferencia del algoritmo determinista que siempre devuelve el mismo resultado con los mismos datos de entrada, el algoritmo probabilista puede devolver distintas soluciones.
Se basa en contraer repetidamente aristas seleccionadas aleatoriamente del grafo hasta llegar a un grafo contraído con dos nodos, cuya arista representará un corte mínimo de aristas en el grafo original. El algoritmo Karger-Stein aplica una mejora al anterior haciéndolo más eficiente.
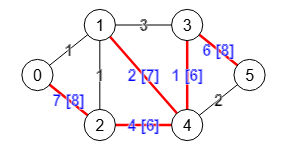
El árbol Gomory-Hu de un grafo permite encontrar el corte mínimo de aristas con menor coste que otros algoritmos cuando se aplica sobre grafos no dirigidos y conectados y, especialmente, sobre grafos ponderados.
Implementamos el algoritmo getGomoryHuTree() para construir ese árbol y también findEdgeCutGomoryHu() para encontrar las aristas de corte mínimo en un grafo a partir de ese árbol.