El problema de los caminos mínimos
getShortestPathFloyd(), como el que se expone aquí con algunas mejoras.Camino mínimo entre dos nodos de un grafo
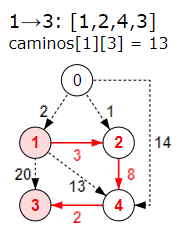
Este problema trata de descubrir los caminos mínimos de todas las parejas de nodos de un un grafo con n nodos. En la Figura puede ver el camino mínimo entre el nodo 1 y el 3. Entre los tres caminos posibles tenemos 1→3 con valor 20, 1→4→3 con valor 13+2=15 y, finalmente, 1→2→4→3 con valor 3+8+2=13, siendo este último el de menor valor.
Vimos algo parecido en el tema del algoritmo de Dijkstra para descubrir el camino mínimo desde un nodo seleccionado, que denominábamos como nodo raíz, al resto de nodos. Podríamos modificar aquel algoritmo para iterar por un bucle de tal forma que en cada iteración designáramos como nodo seleccionado a cada uno de ellos. Aquel era un algoritmo voraz, pero usando programación dinámica podemos utilizar el algoritmo de Floyd que encuentra esos caminos de una forma más simple.
| i ↓ | j → | ||||
|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | |
| 0 | ∞ | 2 | 1 | ∞ | 14 |
| 1 | ∞ | ∞ | 3 | 20 | 13 |
| 2 | ∞ | ∞ | ∞ | ∞ | 8 |
| 3 | ∞ | ∞ | ∞ | ∞ | ∞ |
| 4 | ∞ | ∞ | ∞ | 2 | ∞ |
En el tema del algoritmo de Dijkstra hablábamos del array de longitudes. No es otra cosa que la matriz de adyacencias del grafo. Para el grafo de la Figura esa matriz de adyacencias o array de longitudes es el que se observa en la tabla adjunta, donde utilizamos el valor ∞ para denotar la ausencia de arista entre dos nodos.
Por ejemplo, las posiciones G[0][4]=14 y G[4][0]=∞ significan que los nodos 0 y 4 están conectados con una arista de valor 14 en la dirección 0→4.
El array de longitudes no es otra cosa que la tabla de resultados intermedios que hemos visto en los temas anteriores sobre programación dinámica. En esa tabla está implícita la información para descubrir los caminos mínimos. Recordemos el principio de optimalidad que dice que en una secuencia de decisiones óptimas cualquier subsecuencia también es óptima.
Si observamos el grafo de la Figura, el camino óptimo 1→3 pasa por los nodos 2 y 4. Ese camino comprende los subcaminos 1→2, 2→4 y 4→3, subcaminos también óptimos. Manejaremos un array de caminos que inicialmente será una copia del array de longitudes, definiéndose que al final del proceso C[i][j] contendrá el valor del camino i→j que puede pasar por cero o más nodos.
Para actualizar la información del array de caminos C iteramos por todos los nodos. Cuando lleguemos al nodo k resolveremos la información Ck de los caminos mínimos que usen los nodos intermedios {0, 1, 2, ..., k}. Para ello vemos que previamente tendremos la información del nodo k-1 con Ck-1 usando los nodos {0, 1, 2, ..., k-1}. Para resolver para k utilizaremos la expresión Ck[i][j] = min(Ck-1[i][j], Ck-1[i][k] + Ck-1[k][j]) que se basa en la información previa k-1 usando el principio de optimalidad. Es evidente que en la iteración k el camino mínimo entre i y j es que exista una arista directa o bien será el camino que previamente hemos obtenido en la iteración k-1.
Si iteramos k=0 hasta k=n-1 veremos como va actualizándose el array de caminos C. Recuerde que Ck-1 es el array de camino en la situación anterior, por lo que C-1 contiene la información del array de longitudes al inicio, antes de empezar a iterar. El estado de C en cada etapa se muestra a continuación:
INICIO, C-1 = [[0, 2, 1, ∞, 14], [∞, 0, 3, 20, 13], [∞, ∞, 0, ∞, 8], [∞, ∞, ∞, 0, ∞], [∞, ∞, ∞, 2, 0]]
k = 0, C0 = [[0, 2, 1, ∞, 14], [∞, 0, 3, 20, 13], [∞, ∞, 0, ∞, 8], [∞, ∞, ∞, 0, ∞], [∞, ∞, ∞, 2, 0]]
k = 1, C1 = [[0, 2, 1, 22, 14], [∞, 0, 3, 20, 13], [∞, ∞, 0, ∞, 8], [∞, ∞, ∞, 0, ∞], [∞, ∞, ∞, 2, 0]]
k = 2, C2 = [[0, 2, 1, 22, 9], [∞, 0, 3, 20, 11], [∞, ∞, 0, ∞, 8], [∞, ∞, ∞, 0, ∞], [∞, ∞, ∞, 2, 0]]
k = 3, C3 = [[0, 2, 1, 22, 9], [∞, 0, 3, 20, 11], [∞, ∞, 0, ∞, 8], [∞, ∞, ∞, 0, ∞], [∞, ∞, ∞, 2, 0]]
k = 4, C4 = [[0, 2, 1, 11, 9], [∞, 0, 3, 13, 11], [∞, ∞, 0, 10, 8], [∞, ∞, ∞, 0, ∞], [∞, ∞, ∞, 2, 0]]
Finalmente en C4 tenemos la información de los caminos mínimos. Vemos que C[1][3] = 13 es el valor del camino mínimo en el recorrido 1→3. Luego veremos que podemos extraer la información de los nodos por donde pasa ese camino a partir del array de caminos. Se trata de iterar por punteros hasta que apunte a un índice -1. Extraemos el índice del puntero y lo guardamos en nodosCamino, volviendo a extraer otro puntero en la posición i, puntero.
Algoritmo de Floyd para descubrir los caminos mínimos
El algoritmo de Floyd para descubrir los caminos mínimos es el siguiente.
function floyd(lengths=[]){
let n = lengths[0].length;
let caminos = lengths.map(v => [...v]);
let punteros = lengths.map((v,i) => v.
map((w,j) => i===j || lengths[i][j]===Infinity ? -1 : i));
for (let k=0; k<n; k++){
for (let i=0; i<n; i++){
for (let j=0; j<n; j++){
if (caminos[i][k]+caminos[k][j] < caminos[i][j]) {
caminos[i][j] = caminos[i][k]+caminos[k][j];
punteros[i][j] = punteros[k][j];
}
}
}
}
return {caminos, punteros};
}El array de longitudes lengths nos vendrá como un argumento. De hecho ese array también es la matriz de adyacencia que está definiendo el grafo. Hacemos una copia en caminos. Generamos otro array punteros partiendo del array de longitudes, pero cambiando un valor Infinity por -1. Este array de punteros nos servirá para listar los nodos de un camino. Iteramos k, i, j actualizando ambos arrays cuando caminos[i][k] + caminos[k][j] < caminos[i][j].
El siguiente código obtiene los nodos de todos los caminos. Partiendo de caminos y punteros obtenidos desde floyd(lenghts), en cada iteración i, j creamos un nuevo array nodosCamino que contendrá los índices de los nodos que cubren el camino i→j. Se trata de iterar por el array de punteros encadenados, obteniendo el siguiente como punteros[i][puntero] hasta que lleguemos a un -1.
let {caminos, punteros} = floyd(lengths);
let n = punteros[0].length;
for (let i=0; i<n; i++){
for (let j=0; j<n; j++){
if (i!==j && caminos[i][j]!==null){
let nodosCamino = [];
let puntero = punteros[i][j];
while (puntero > -1){
nodosCamino.unshift(puntero);
puntero = punteros[i][puntero];
}
nodosCamino.push(j);
console.log(i, j, nodosCamino);
}
}
}Por ejemplo, para el camino 1→3 tendremos en nodosCamino el array [1,2,4,3]. Vease que sacamos cada array en la consola, pero en el siguiente ejemplo usaremos código adicional para preparar la visualización del grafo con ese camino resaltado.
Ejemplo: Algoritmo de Floyd: Caminos mínimos
Ejemplo de creación propia.
floyd(grafo):El coste del algoritmo de Floyd
Para hablar sobre el coste no perdemos generalidad si consideramos que los arrays se inician en uno en lugar de cero. Como el bucle triple del algoritmo de Floyd realiza iteraciones k=1..n × i=1..n × j=1..n, el coste es cúbico O(n3). No se tiene en cuenta la creación de los arrays caminos y punteros pues ambos tiene un coste n2, por lo que el coste en secuencia del bucle triple domina sobre éste. Incluso el coste del bucle para visualizar los caminos tiene un coste que no será superior al cúbico. Si hubiésemos usado el algoritmo de Dijkstra que tenía un coste de O(n2), tendríamos que ejecutarlo n veces, por lo que el coste sería también cúbico. Sin embargo el algoritmo de Floyd es más simple de ejecutar, siendo en la práctica más rápido que los n Dijkstra.