18 sep 2025

Componentes conectados en grafos

Obtener componentes conectados `getConnectedComponents()`

*Figura*. Componentes conectados en un grafo no dirigido

Un grafo conectado es aquel donde desde un nodo podemos llegar a cualquier otro del grafo. En otro caso pueden existir subgrafos conectados que son aquellos donde todos los nodos del subgrafo están conectados. Si el grafo es dirigido podemos hablar de débilmente conectado si no consideramos la dirección de las aristas, es decir, si consideramos el grafo como no dirigido. Y fuertemente conectado cuando se considera la dirección de las aristas.

Los términos conectado y conexo son sinónimos en este contexto. Así por ejemplo a veces diremos en estos temas grafo conectado o grafo conexo refiriéndonos a lo mismo.

Si un grafo es conectado tendrá un único componente conectado. En otro caso habrá tantos componentes conectados como subgrafos conectados.

Componentes conectados: [
{"visited":[0,1,4,7],
"path":[[0,1],[1,4],[4,7]]},
{"visited":[2,3,6,5,8],
"path":[[2,3],[3,6],[6,5],[6,8]]}
]

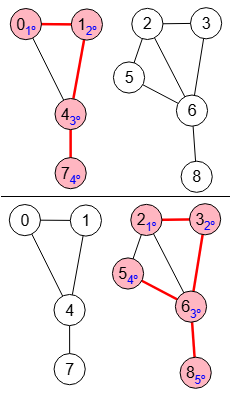
En la Figura vemos los dos componentes conectados de un grafo no dirigido. El grafo no es conectado pero tiene 2 subgrafos conectados. La aplicación devuelve este resultado, con dos entradas, donde vemos los nodos de cada componente en "visited" y el camino seguido para descubrirlos en "path". Esta estructura del resultado es la que devuelve el algoritmo de búsqueda en profundidad recursiva getDepthFirstSearchRecursive() que vimos en un tema anterior, que sirve de base para obtener los componentes conectados de un grafo no dirigido, como veremos después.

En la aplicación accedemos a cada componente conectado con los botones de navegación que se encuentran junto al grafo. Y para presentarlo aquí hemos compuesto la imagen de la Figura separando cada grafo con una línea.

Con el siguiente JSON puede importar ese ejemplo:

{"nodes":[
    {"index":0,"nodeOffset":"-23.36 0.77","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"17.74 -24.06","parent":[{"index":0}]},
    {"index":2,"nodeOffset":"-8.02 0.71","parent":[{"index":-1}]},
    {"index":3,"nodeOffset":"48.85 -24.57","parent":[{"index":2}]},
    {"index":4,"nodeOffset":"-22.12 11.84","parent":[{"index":0},{"index":1}]},
    {"index":5,"nodeOffset":"-15.38 -2.81","parent":[{"index":2}]},
    {"index":6,"nodeOffset":"-6.81 10.47","parent":[{"index":2},{"index":3},{"index":5}]},
    {"index":7,"nodeOffset":"-5.42 10.54","parent":[{"index":4}]},
    {"index":8,"nodeOffset":"11.73 11.99","parent":[{"index":6}]}
],
"config":{
    "algorithm":"Get connected components"
}}

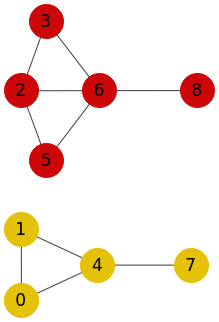
En la Figura vemos los mismos dos componentes conectados del grafo no dirigido en Wolfram que obtuvimos en nuestra aplicación, donde Wolfram colorea cada componente. Usa la función ConnectedComponents.

g = AdjacencyGraph[{{0,1,0,0,1,0,0,0,0},{1,0,0,0,1,0,0,0,0},{0,0,0,1,0,1,1,0,0},{0,0,1,0,0,0,1,0,0},{1,1,0,0,0,0,0,1,0},
{0,0,1,0,0,0,1,0,0},{0,0,1,1,0,1,0,0,1},{0,0,0,0,1,0,0,0,0},{0,0,0,0,0,0,1,0,0}}, ImageSize->219, 
VertexSize->{"Scaled", 0.1}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center], 3->Placed[2,Center], 
4->Placed[3,Center], 5->Placed[4,Center], 6->Placed[5,Center], 7->Placed[6,Center], 8->Placed[7,Center], 9->Placed[8,Center]}, 
VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold], VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}];
ConnectedComponents[g];
HighlightGraph[g, %]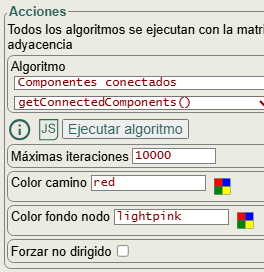

En la Figura vemos las opciones de la aplicación, con color camino y color fondo nodo para el resaltado de los componentes. La opción forzar no dirigido sólo aplica a grafos dirigidos como veremos a continuación.

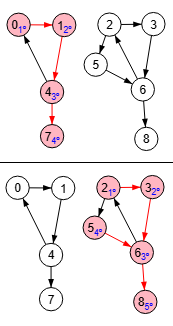
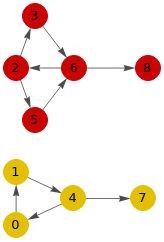
En la Figura vemos un grafo dirigido con los mismos nodos y aristas que el visto al inicio en la Figura al que hemos dado dirección a las aristas, obteniéndose los componentes conectados marcando la opción forzar no dirigido. Los componentes conectados son los mismos que los del grafo no dirigido, conociéndose como componentes débilmente conectados cuando se trata el grafo dirigido como no dirigido.

Componentes conectados: [
{"visited":[0,1,4,7],
"path":[[0,1],[1,4],[4,7]]},
{"visited":[2,3,6,5,8],
"path":[[3,2],[6,3],[5,6],[8,6]]}
]

El resultado para los nodos visitados ("visited") es el mismo que para el grafo no dirigido que vimos al inicio. Las aristas también son las mismas y debemos pensar que aunque se resalten con color en el grafo, se han obtenido tomando el grafo como no dirigido.

{"nodes":[
    {"index":0,"nodeOffset":"-23.36 0.77","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"9.41 -24.06","parent":[{"index":0}]},
    {"index":2,"nodeOffset":"-8.02 0.71","parent":[{"index":-1}]},
    {"index":3,"nodeOffset":"32.18 -24.57","parent":[{"index":2}]},
    {"index":4,"nodeOffset":"-5.45 -13.16","parent":[{"index":1},{"index":0,"markerStart":"none","markerEnd":"arrow"}]},
    {"index":5,"nodeOffset":"-23.71 -2.81","parent":[{"index":2}]},
    {"index":6,"nodeOffset":"9.85 -14.53","parent":[{"index":3},{"index":5},{"index":2,"markerStart":"none","markerEnd":"arrow"}]},
    {"index":7,"nodeOffset":"-5.42 -14.46","parent":[{"index":4}]},
    {"index":8,"nodeOffset":"11.73 -13.01","parent":[{"index":6}]}
],
"config":{
    "lineHeight":18.75,
    "markerStart":"arrow",
    "algorithm":"Get connected components"
}}

En la Figura vemos los mismos dos componentes débilmente conectados en Wolfram, usándose en este caso otra función WeaklyConnectedComponents.

g = AdjacencyGraph[{{0,1,0,0,0,0,0,0,0},{0,0,0,0,1,0,0,0,0},{0,0,0,1,0,1,0,0,0},{0,0,0,0,0,0,1,0,0},
{1,0,0,0,0,0,0,1,0},{0,0,0,0,0,0,1,0,0},{0,0,1,0,0,0,0,0,1},{0,0,0,0,0,0,0,0,0},{0,0,0,0,0,0,0,0,0}}, 
ImageSize->164, VertexSize->{"Scaled", 0.1}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center], 
3->Placed[2,Center], 4->Placed[3,Center], 5->Placed[4,Center], 6->Placed[5,Center], 7->Placed[6,Center], 
8->Placed[7,Center], 9->Placed[8,Center]}, VertexLabelStyle->Directive[Black,13.13], EdgeLabelStyle->Directive[Black,13.13,Bold], 
VertexStyle->White, DirectedEdges->True, EdgeStyle->{{Black,Thickness[0.005]}}];
WeaklyConnectedComponents[g];
HighlightGraph[g, %]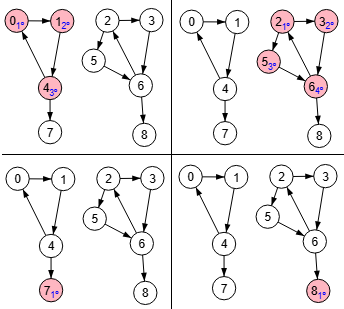

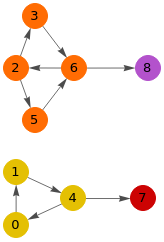
Cuando se consideran la dirección de las aristas en un grafo dirigido, entonces obtenemos los componentes fuertemente conectados. En la Figura vemos que se encuentran 4 componentes fuertemente conectados en el grafo dirigido usando el ejemplo anterior.

Componentes conectados: [
{"visited":[0,1,4],"path":[]},
{"visited":[2,3,5,6],"path":[]},
{"visited":[7],"path":[]},
{"visited":[8],"path":[]}
]

En la Figura vemos los mismos 4 componentes fuertemente conectados que se obtienen en Wolfram, cada uno con un color diferente. Utiliza la misma función ConnectedComponents que para el grafo no dirigido.

g = AdjacencyGraph[{{0,1,0,0,0,0,0,0,0},{0,0,0,0,1,0,0,0,0},{0,0,0,1,0,1,0,0,0},{0,0,0,0,0,0,1,0,0},
{1,0,0,0,0,0,0,1,0},{0,0,0,0,0,0,1,0,0},{0,0,1,0,0,0,0,0,1},{0,0,0,0,0,0,0,0,0},{0,0,0,0,0,0,0,0,0}}, 
ImageSize->164, VertexSize->{"Scaled", 0.1}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center], 
3->Placed[2,Center], 4->Placed[3,Center], 5->Placed[4,Center], 6->Placed[5,Center], 7->Placed[6,Center], 
8->Placed[7,Center], 9->Placed[8,Center]}, VertexLabelStyle->Directive[Black,13.13], EdgeLabelStyle->Directive[Black,13.13,Bold], 
VertexStyle->White, DirectedEdges->True, EdgeStyle->{{Black,Thickness[0.005]}}];
ConnectedComponents[g];
HighlightGraph[g, %]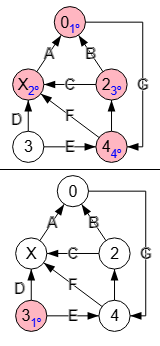

El grafo dirigido de la Figura no es conectado, pues desde cualquiera de los nodos 0,1,2,4 no podemos llegar al nodo 3. Pero tiene 2 componentes fuertemente conectados.

Componentes conectados: [
{"visited":[0,1,2,4],"path":[]},
{"visited":[3],"path":[]}
]

{"nodes":[
    {"index":0,"parent":[{"index":-1}]},
    {"index":1,"value":"X","parent":[{"index":0,"value":"A"}]},
    {"index":2,"parent":[{"index":0,"value":"B"},{"index":1,"value":"C"}]},
    {"index":3,"parent":[{"index":1,"value":"D","lineTextOffset":"-0.75 0.25"},{"index":4,"value":"E"}]},
    {"index":4,"parent":[{"index":1,"value":"F"},{"index":2},{"index":0,"lineOffset":"1","markerReverse":true,"value":"G"}]}
],
"config":{
    "markerEnd":"arrow",
    "algorithm":"Get connected components"
}}

Vemos en la Figura los 2 mismos componentes fuertemente conectados en Wolfram.

g = AdjacencyGraph[{{0,0,0,0,1},{1,0,0,0,0},{1,1,0,0,0},{0,1,0,0,1},{0,1,1,0,0}}, ImageSize->188, VertexSize->{"Scaled", 0.17}, 
VertexLabels->{1->Placed[0,Center], 2->Placed["X",Center], 3->Placed[2,Center], 4->Placed[3,Center], 5->Placed[4,Center]}, 
VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold], EdgeLabels->{(2->1)->"A", (3->1)->"B", (3->2)->"C", 
(4->2)->"D", (4->5)->"E", (5->2)->"F", (1->5)->"G"}, VertexStyle->White, DirectedEdges->True, EdgeStyle->{{Black,Thickness[0.005]}}];
ConnectedComponents[g];
HighlightGraph[g, %]

A continuación vemos el JavaScript para ejecutar getConnectedComponents(). Su ejecución se desglosa en dos partes. La primera es para grafos no dirigidos o dirigidos que se fuerzan a no dirigidos con el argumento forceUndirected = true, usándose la búsqueda en profundidad recursiva mediante el algoritmo getDepthFirstSearchRecursive(), pues cada búsqueda devolverá un subconjunto de nodos conectados.

La segunda parte es para obtener los componentes fuertemente conectados de un grafo dirigido, para los que tenemos que usar otra estrategia. Se trata de ver los caminos que hay entre dos nodos del grafo, en una y otra dirección, usando el algoritmo para encontrar caminos entre dos nodos findPath(). Si hay camino en las dos direcciones se agrega ese nodo a un componente. Los nodos que al final no estén en ningún componente serán componentes con nodos aislados.

Se usa isGraphDirected() para saber si el grafo es dirigido.

function getConnectedComponents({matrix=[], forceUndirected=true}){
    let result = [], temp;
    try {
        let directed = isGraphDirected({matrix});
        if (typeof directed==="string") throw new Error(directed);
        let n = matrix.length;
        let isInComponent = Array.from({length: n}, () => false);
        if (!directed || forceUndirected) {
            for (let index=0; index<n; index++) {
                if (!isInComponent[index]) {
                    let temp = getDepthFirstSearchRecursive({matrix, index, forceUndirected});
                    if (typeof temp==="string") throw new Error(temp);
                    temp.visited.forEach(v => isInComponent[v]=true);
                    result.push(temp);
                }
            }
        } else {
            let components = [];
            for (let i=0; i<n; i++) {
                if (!isInComponent[i]) {
                    isInComponent[i] = true;
                    let newComponent = [i];
                    for (let j=i+1; j<n; j++) {
                        if (!isInComponent[j]) {
                            let paths = findPath({matrix, firstIndex:i, lastIndex:j});
                            if (typeof paths==="string") throw new Error(paths);
                            let pathsReverse = findPath({matrix, firstIndex:j, lastIndex:i});
                            if (typeof pathsReverse==="string") throw new Error(pathsReverse);
                            if (paths.length>0 && pathsReverse.length>0) {
                                isInComponent[j] = true;
                                newComponent.push(j);
                            }
                        }
                    }
                    components.push(newComponent);
                }
            }
            components.forEach(v => result.push({visited: v, path: []}));
            let notInComponent = isInComponent.map((v,i) => [i, v]).filter(v => !v[1]).map(v => v[0]);
            notInComponent.forEach(v => result.push({visited: [v], path: []}));
        }
    } catch(e){result = e.message}
    return result;
}

El algoritmo anterior no es el más eficiente para obtener los componentes fuertemente conectados en grafos dirigidos, pudiendo encontrar otros como los algoritmos de Kosaraju, Tarjan y el algoritmo basado en caminos con varias versiones, una de ella de Dijkstra. No he implentado ninguno de estos algoritmos en la aplicación.

Es el grafo conectado `isGraphConnected()`

Con el algoritmo isGraphConnected() verificamos si un grafo es conectado, o equivalentemente si es conexo. Un grafo es conectado si desde cualquier nodo podemos llegar a cualquier otro nodo siguiendo las aristas.

Time: 0 ms

Es el grafo conectado:
false

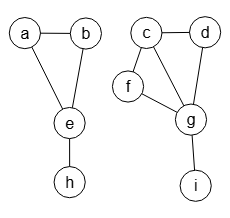
En la Figura vemos un grafo no dirigido que no es conectado, devolviendo la aplicación sólo el booleano verdadero o falso.

{"nodes":[
    {"index":0,"nodeOffset":"-23.36 0.77","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"17.74 -24.06","parent":[{"index":0}]},
    {"index":2,"nodeOffset":"-8.02 0.71","parent":[{"index":-1}]},
    {"index":3,"nodeOffset":"48.85 -24.57","parent":[{"index":2}]},
    {"index":4,"nodeOffset":"-22.12 11.84","parent":[{"index":0},{"index":1}]},
    {"index":5,"nodeOffset":"-15.38 -2.81","parent":[{"index":2}]},
    {"index":6,"nodeOffset":"-6.81 10.47","parent":[{"index":2},{"index":3},{"index":5}]},
    {"index":7,"nodeOffset":"-5.42 10.54","parent":[{"index":4}]},
    {"index":8,"nodeOffset":"11.73 11.99","parent":[{"index":6}]}
],
"config":{
    "nodeValueAuto":"alphabetic-lower",
    "algorithm":"Is graph connected"
}}

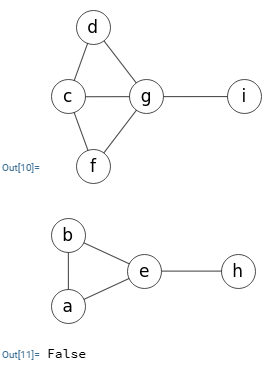
En la Figura vemos la exportación a Wolfram que usa la función ConnectedGraphQ[g], devolviendo también falso. Se ajusta el tamaño de los vértices tal como se observa en la Figura.

g = AdjacencyGraph[{{0,1,0,0,1,0,0,0,0},{1,0,0,0,1,0,0,0,0},{0,0,0,1,0,1,1,0,0},{0,0,1,0,0,0,1,0,0},{1,1,0,0,0,0,0,1,0},
{0,0,1,0,0,0,1,0,0},{0,0,1,1,0,1,0,0,1},{0,0,0,0,1,0,0,0,0},{0,0,0,0,0,0,1,0,0}}, 
ImageSize->219, VertexSize->{"Scaled", 0.1}, VertexLabels->{1->Placed["a",Center], 2->Placed["b",Center], 
3->Placed["c",Center], 4->Placed["d",Center], 5->Placed["e",Center], 6->Placed["f",Center], 7->Placed["g",Center], 
8->Placed["h",Center], 9->Placed["i",Center]}, VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold], 
VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}];

ConnectedGraphQ[g]

En la Figura vemos la opción forzar no dirigido, única opción para saber si un grafo es conectado. Si el grafo es no dirigido se ignora esa opción. Si el grafo es dirigido y se marca la opción se trata el grafo como si fuera no dirigido, con lo que estaríamos cuestionando si el grafo es débilmente conectado. Si el grafo es dirigido y no se marca la opción, entonces la cuestión es saber si el grafo es fuertemente conectado.

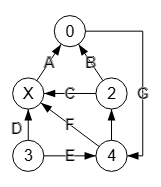
En la Figura vemos un grafo dirigido NO fuertemente conectado pero SÍ débilmente conectado. La aplicación sólo devuelve true o false, con lo que se determina si está conectado, débilmente conectado o fuertemente conectado observado la direccionalidad del grafo y el argumento para forzar no dirigido:

Dirigido	Forzar no dirigido	isGraphConnected()
NO	-	¿Conectado?
SÍ	SÍ	¿Débilmente conectado?
SÍ	NO	¿Fuertemente conectado?

Observe que en la Figura del apartado anterior obtuvimos 2 componentes fuertemente conectados, con lo que el grafo NO es fuertemente conectado pues para serlo sólo debería tener UN único componente fuertemente conectado.

Con este JSON se importa el ejemplo cuestionando si el grafo es fuertemente conectado, pues es dirigido y no activamos la opción forzar no dirigido. El resultado es que NO es fuertemente conectado:

{"nodes":[
    {"index":0,"parent":[{"index":-1}]},
    {"index":1,"value":"X","parent":[{"index":0,"value":"A"}]},
    {"index":2,"parent":[{"index":0,"value":"B"},{"index":1,"value":"C"}]},
    {"index":3,"parent":[{"index":1,"value":"D","lineTextOffset":"-0.75 0.25"},{"index":4,"value":"E"}]},
    {"index":4,"parent":[{"index":1,"value":"F"},{"index":2},{"index":0,"lineOffset":"1","markerReverse":true,"value":"G"}]}
],
"config":{
    "markerEnd":"arrow",
    "algorithm":"Is graph connected"
}}

Con este JSON se importa el ejemplo cuestionando si el grafo es débilmente conectado, pues es dirigido y activamos la opción forzar no dirigido. El resultado es que SÍ es débilmente conectado:

{"nodes":[
    {"index":0,"parent":[{"index":-1}]},
    {"index":1,"value":"X","parent":[{"index":0,"value":"A"}]},
    {"index":2,"parent":[{"index":0,"value":"B"},{"index":1,"value":"C"}]},
    {"index":3,"parent":[{"index":1,"value":"D","lineTextOffset":"-0.75 0.25"},{"index":4,"value":"E"}]},
    {"index":4,"parent":[{"index":1,"value":"F"},{"index":2},{"index":0,"lineOffset":"1","markerReverse":true,"value":"G"}]}
],
"config":{
    "markerEnd":"arrow",
    "algorithm":"Is graph connected",
    "forceUndirected":true
}}

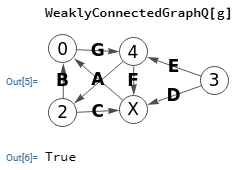
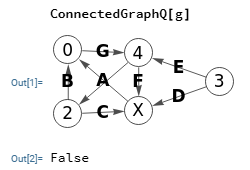
En Wolfram obtenemos lo mismo, pues en la Figura vemos que el grafo SÍ es débilmente conectado aplicando la función WeaklyConnectedGraphQ[g]. Y en la Figura vemos que NO es fuertemente conectado aplicando la función ConnectedGraphQ[g].

g = AdjacencyGraph[{{0,0,0,0,1},{1,0,0,0,0},{1,1,0,0,0},{0,1,0,0,1},{0,1,1,0,0}}, ImageSize->188,
VertexSize->{"Scaled", 0.17}, VertexLabels->{1->Placed[0,Center], 2->Placed["X",Center], 3->Placed[2,Center], 
4->Placed[3,Center], 5->Placed[4,Center]}, VertexLabelStyle->Directive[Black,17.5], 
EdgeLabelStyle->Directive[Black,17.5,Bold], EdgeLabels->{(2->1)->"A", (3->1)->"B", (3->2)->"C", (4->2)->"D", (4->5)->"E", (5->2)->"F", (1->5)->"G"}, 
VertexStyle->White, DirectedEdges->True, EdgeStyle->{{Black,Thickness[0.005]}}]
WeaklyConnectedGraphQ[g]

Hay que entender que todo grafo fuertemente conectado es también débilmente conectado pero no necesariamente al revés, con lo que es mejor aclarar todas las posibilidades que tenemos para un grafo dirigido en la siguiente tabla, donde se expone un grafo dirigido de ejemplo para cada caso:

Grafo dirigido	Débilmente conectado	Fuertemente conectado	Matriz	JSON
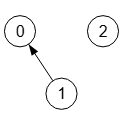	NO	NO	0 0 0 1 0 0 0 0 0	{"nodes":[ {"index":0,"parent":[{"index":-1}]}, {"index":1,"parent":[{"index":0}]}, {"index":2,"parent":[{"index":-1}]} ], "config":{ "markerEnd":"arrow", "algorithm":"Is graph connected" }}
No existe	NO	SÍ	Todo grafo fuertemente conectado es también débilmente conectado
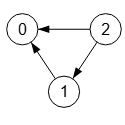	SÍ	NO	0 0 0 1 0 0 1 1 0	{"nodes":[ {"index":0,"parent":[{"index":-1}]}, {"index":1,"parent":[{"index":0}]}, {"index":2,"parent":[{"index":-1},{"index":0},{"index":1}]} ], "config":{ "markerEnd":"arrow", "algorithm":"Is graph connected", "forceUndirected":true }}
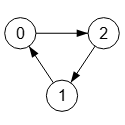	SÍ	SÍ	0 0 1 1 0 0 0 1 0	{"nodes":[ {"index":0,"parent":[{"index":-1},{"index":2}]}, {"index":1,"parent":[{"index":0}]}, {"index":2,"parent":[{"index":-1},{"index":1}]} ], "config":{ "markerEnd":"arrow", "algorithm":"Is graph connected" }}

El código JavaScript para ejecutar isGraphConnected() que se expone a continuación usa lo siguiente:

isGraphDirected() para saber si un grafo es dirigido.
getDepthFirstSearchRecursive() para realizar una búsqueda en profundidad.
getConnectedComponents para obtener los componentes conectados.

Si el grafo no es dirigido o se fuerza a no dirigido sólo basta hacer una búsqueda en profundidad y observar que el total de nodos visitados coincide con el total de nodos del grafo.

Si el grafo es dirigido y no se fuerza a no dirigido obtenemos los componentes fuertemente conectados como vimos en el apartado anterior, observando que sólo se obtiene un único componente.

function isGraphConnected({matrix=[], forceUndirected=false}){
    let result = false, temp;
    try {
        let directed = isGraphDirected({matrix});
        if (typeof directed==="string") throw new Error(directed);
        let n = matrix.length;
        if (!directed || forceUndirected) {
            if (temp = getDepthFirstSearchRecursive({matrix, index:0, forceUndirected}), typeof temp==="string") throw new Error(temp);
            result = temp.visited.length === n;
        } else {
            if (temp = getConnectedComponents({matrix, forceUndirected:false}), temp.error) throw new Error(temp.error);
            result = temp.length===1;
        }
    } catch(e){result = e.message}
    return result;
}

Convertir a fuertemente conectado `convertToStronglyConnected()`

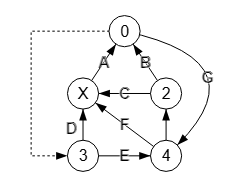
En el apartado anterior vimos que el grafo de la Figura sin considerar la arista punteada 0🡒3 no era fuertemente conectado, pues no había forma de llegar al nodo "3" desde cualquiera de los otros nodos. La ejecución del algoritmo isGraphConnected() para ese grafo sin esa arista devolverá falso. Si agregamos la arista 0🡒3 podemos recorrer todos los los nodos partiendo desde uno cualquiera, devolviendo isGraphConnected() verdadero.

Con el algoritmo convertToStronglyConnected() convertimos un grafo dirigido y no fuertemente conectado en uno fuertemente conectado. El algoritmo devuelve la nueva matriz de adyacencia y las aristas que se han agregado para esa conversión. En el ejemplo vemos que se devuelve "newEdges":[[0,3,""]] con la arista 0🡒3 que para este grafo tiene un valor "", representándose con una línea de puntos.

Convertir a fuertemente conectado: {
"matrix":
[[null,null,null,"","G"],
["A",null,null,null,null],
["B","C",null,null,null],
[null,"D",null,null,"E"],
[null,"F","",null,null]],
"newEdges":[[0,3,""]]
}

En la opción lineTypeNewEdges (tipo línea nuevas aristas) podemos pasar una lista de tipos de aristas y desplazamientos (lineOffset), valores que se aplicarán en el mismo orden a las nuevas aristas que el algoritmo genera. Así con rect -3 se aplica a la primera y única nueva arista un deplazamiento de 3 unidades horizontales a la izquierda usando un tipo de línea recta.

{"nodes":[
    {"index":0,"parent":[{"index":-1}]},
    {"index":1,"value":"X","parent":[{"index":0,"value":"A"}]},
    {"index":2,"parent":[{"index":0,"value":"B"},{"index":1,"value":"C"}]},
    {"index":3,"parent":[{"index":1,"value":"D","lineTextOffset":"-0.75 0.25"},{"index":4,"value":"E"}]},
    {"index":4,"parent":[{"index":1,"value":"F"},{"index":2},{"index":0,"lineOffset":"8 -2","markerReverse":true,"lineType":"quadratic","value":"G"}]}
],
"config":{
    "markerEnd":"arrow",
    "algorithm":"Convert to strongly connected",
    "lineTypeNewEdges":"rect -3"
}}

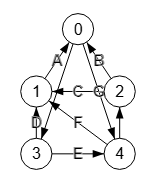
Si importamos la matriz que devuelve el algoritmo observamos que ya incluye la arista 0🡒3.

[[null,null,null,"","G"],
["A",null,null,null,null],
["B","C",null,null,null],
[null,"D",null,null,"E"],
[null,"F","",null,null]]

A continuación vemos el JavaScript del algoritmo convertToStronglyConnected(), usando los algoritmos isGraphDirected() para saber si el grafo es dirigido pues sólo aplica a dirigidos, getMatrixModeValue() para obtener el modo valores de la matriz y el valor nulo nullValue dado que isGraphConnected() para saber si el grafo es conectado sólo aplica a matrices con valores numéricos.

function convertToStronglyConnected({matrix=[]}){
    let result = {matrix, newEdges:[]}, temp;
    try {
        let n = matrix.length;
        if (temp = isGraphDirected({matrix}), typeof temp==="string") throw new Error(temp);
        let directed = temp;
        if (directed) {
            if (temp = getMatrixModeValue({matrix}), typeof temp==="string") throw new Error (temp);
            let [modeValue, nullValue] = temp;
            let matrixCopy;
            if (nullValue===0){
                matrixCopy = matrix;
            } else {
                matrixCopy = [];
                for (let i=0; i<n; i++){
                    let arr = [];
                    for (let j=0; j<n; j++){
                        arr.push(matrix[i][j]===nullValue ? 0 : 1);
                    }
                    matrixCopy.push(arr);
                }
            }
            if (temp = isGraphConnected({matrix:matrixCopy}), typeof temp==="string") throw new Error(temp);
            let connected = temp;
            if (!connected) {
                if (temp = getTotalEdges({matrix}), typeof temp==="string") throw new Error(temp);
                let totalEdges = temp;
                let newValue = (modeValue==="0/1" || modeValue==="0/number") ? Math.max(...matrix.flat()) * totalEdges : 
                    modeValue==="null/value" ? "" : true;
                let n = matrix.length;
                for (let i=0; i<n; i++) {
                    if (matrix[i].every((v,j) => i===j || v===nullValue)) {
                        let k = i===0 ? n-1 : 0;
                        matrix[i][k] = newValue;
                        result.newEdges.push([i, k, newValue]);
                    }
                }
                for (let j=0; j<n; j++) {
                    let all0 = true;
                    for (let i=0; i<n; i++) {
                        if (i!==j && matrix[i][j]!==nullValue) {
                            all0 = false;
                            break;
                        }
                    }
                    if (all0) {
                        let k = j===0 ? n-1 : 0;
                        matrix[k][j] = newValue;
                        result.newEdges.push([k, j, newValue]);
                    }
                }
            }
        }
    } catch(e){result = e.message}
    return result;
}

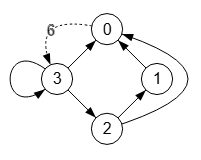
Para convertir a fuertemente conectado el grafo de la Figura necesitamos agregar la arista 0🡒3. Vemos que se le adjudica un peso 6 dado que el grafo tiene valores unitarios de las aristas que es cuando ninguna arista tiene valor especificado. El valor 6 resulta de obtener el mayor valor de todas las aristas y multiplicarlo por el total de aristas, operación que es necesaria para algoritmos que veremos en otros temas.

En el algoritmo tras detectar que es dirigido y no conectado, obtemos las aristas faltantes observando su matriz de adyacencia.

Buscamos todas las filas y columnas con todos ceros, a excepción de la diagonal donde puede haber un 1 de un autobucle como el de 3🡒3, arista que no influye para saber si es fuertemente conectado. Vemos la fila 0 y la columna 3, así que es necesaria la arista 0🡒3 para que sea un grafo fuertemente conectado.

{"nodes":[
    {"index":0,"nodeOffset":"1.6","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"21.6 -5","parent":[{"index":0}]},
    {"index":2,"nodeOffset":"1.6 -10","parent":[{"index":1},{"index":0,"lineOffset":10.37,"lineType":"quadratic"}]},
    {"index":3,"nodeOffset":"-18.4 -55","parent":[{"index":2},{"index":0},{"index":3,"lineType":"cubic","lineOffset":"-4 -4 -4 4"}]}
],
"config":{
    "markerEnd":"arrow",
    "algorithm":"Convert to strongly connected",
    "lineTypeNewEdges":"quadratic -4 -3"
}}

Es el grafo totalmente desconectado `isGraphAllDisconnected()`

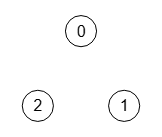
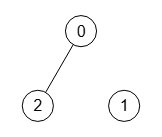
En el apartado anterior vimos el algoritmo IsGraphConnected() que nos decía si un grafo es o no conectado. Pero esa información no es suficiente para saber si el grafo está totalmente desconectado en el sentido de que todos sus nodos están desconectados, o lo que es lo mismo, que el grafo no tiene aristas. Los dos grafos de la Figura y de la Figura son ambos desconectados, pero sólo el primero es totalmente desconectado.

Con estos dos JSON puede importar esos ejemplos:

{"nodes":[
    {"index":0,"nodeOffset":"7.5","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"-0.18 30","parent":[{"index":-1}]},
    {"index":2,"nodeOffset":"-59.82 30","parent":[{"index":-1}]}
],
"config":{
    "algorithm":"Is graph all disconnected"
}}

{"nodes":[
    {"index":0,"nodeOffset":"7.5 0","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"-0.18 30","parent":[{"index":-1}]},
    {"index":2,"nodeOffset":"-59.82 30","parent":[{"index":-1},{"index":0}]}
],
"config":{
    "algorithm":"Is graph connected"
}}

El código JavaScript para ejecutar isGraphAllDisconnected() es el siguiente, usando getMatrixModeValue() para obtener el modo valores de la matriz y el valor nulo nullValue. Así cuando una matriz de adyacencia tiene todo los valores nulos significa que no tiene aristas y, por tanto, es totalmente desconectado.

function isGraphAllDisconnected({matrix=[]}){
    let result = false, temp;
    try {
        if (temp = getMatrixModeValue({matrix}), typeof temp==="string") throw new Error (temp);
        let [modeValue, nullValue] = temp;
        result = matrix.flat().every(v => v===nullValue);
    } catch(e){result = e.message}
    return result;
}

No veo en Wolfram una función específica para esto. Podría pensarse que usando getConnectedComponents(), o su equivalente ConnectedComponents en Wolfram, podría deducirse si un grafo es totalmente desconectado. Pero el siguiente ejemplo demuestra que no es tan simple como se plantea.

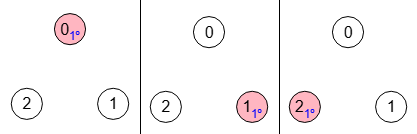
En la Figura vemos los 3 componentes conectados de un grafo sin aristas, siendo por ello totalmente desconectado.

Componentes conectados: [
{"visited":[0],"path":[]},
{"visited":[1],"path":[]},
{"visited":[2],"path":[]}]

Podría deducirse que es totalmente desconectado pues el número de componentes conectados es igual que el número de nodos del grafo, con cada componente conectado con un único nodo. Pero a continuación veremos que no es suficiente.

{"nodes":[
    {"index":0,"nodeOffset":"7.5","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"-0.18 30","parent":[{"index":-1}]},
    {"index":2,"nodeOffset":"-59.82 30","parent":[{"index":-1}]}
],
"config":{
    "markerEnd":"arrow",
    "algorithm":"Get connected components"
}}

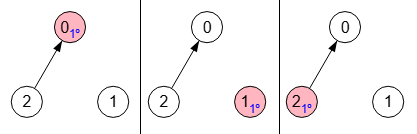
El grafo dirigido de la Figura también tienes 3 componentes fuertemente conectados, pero no es totalmente desconectado dado que existe la arista "2🡒0".

Componentes conectados: [
{"visited":[0],"path":[]},
{"visited":[1],"path":[]},
{"visited":[2],"path":[]}]

Se obtienen los mismos componentes conectados que para el otro ejemplo, con lo que no es suficiente para decidir si el grafo es totalmente desconectado.

{"nodes":[
    {"index":0,"nodeOffset":"7.5","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"-0.18 30","parent":[{"index":-1}]},
    {"index":2,"nodeOffset":"-59.82 30","parent":[{"index":-1},{"index":0}]}
],
"config":{
    "markerEnd":"arrow",
    "algorithm":"Get connected components"
}}

Existe la posibilidad de usar getEdges() de tal forma que si no se obtienen aristas será totalmente desconectado, pero el algoritmo que usamos en nuestra aplicación es mucho más simple y eficiente que el de obtención de aristas. Para exportar a Wolfram sí usamos la obtención de aristas para hacer esa comprobación:

e = EdgeList[g]
Length[e]==0

Es el grafo un árbol `isGraphTree()`

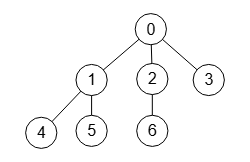
Un grafo no dirigido es un árbol si es conectado y no tiene ciclos. Para ello usamos el algoritmo que vimos antes isGraphConnected() que para el grafo de la Figura nos dice que sí es conectado y también el algoritmo hasCycles() que vimos en un tema anterior que nos dice que no tiene ciclos.

Es el grafo un árbol:
true

El algoritmo isGraphTree() simplemente devuelve true o false.

{"nodes":[
    {"index":0,"nodeOffset":"10.33 -0.8","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"11.64 -5.4","parent":[{"index":0}]},
    {"index":2,"nodeOffset":"10.93 -5.8","parent":[{"index":0}]},
    {"index":3,"nodeOffset":"8.5 -5.4","parent":[{"index":0}]},
    {"index":4,"nodeOffset":"-8.5 -9.2","parent":[{"index":1}]},
    {"index":5,"nodeOffset":"-13.36 -10","parent":[{"index":1}]},
    {"index":6,"nodeOffset":"-14.07 -10","parent":[{"index":2}]}
],
"config":{
    "algorithm":"Is graph tree"
}}

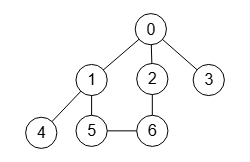
En cambio el grafo de la Figura es también conectado pero SÍ tiene ciclos, no siendo por tanto un árbol. El algoritmo isGraphTree() devuelve en este caso Es el grafo un árbol: false.

{"nodes":[
    {"index":0,"nodeOffset":"10.33 -0.8","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"11.64 -5.4","parent":[{"index":0}]},
    {"index":2,"nodeOffset":"10.93 -5.8","parent":[{"index":0}]},
    {"index":3,"nodeOffset":"8.5 -5.4","parent":[{"index":0}]},
    {"index":4,"nodeOffset":"-8.5 -9.2","parent":[{"index":1}]},
    {"index":5,"nodeOffset":"-13.36 -10","parent":[{"index":1}]},
    {"index":6,"nodeOffset":"-14.07 -10","parent":[{"index":2},{"index":5}]}
],
"config":{
    "algorithm":"Is graph tree"
}}

El JavaScript del algoritmo isGraphTree() es el siguiente, usando isGraphConnected(), hasCycles() y getUndirectedMatrix() para obtener la versión no dirigida si el grafo no lo fuera, pues el grafo debe ser débilmente conectado para el caso de grafos no dirigidos, pues en otro caso no podría ser un árbol.

function isGraphTree({matrix=[]}){
    let result = false;
    try {
        let matrixUndirected = getUndirectedMatrix({matrix});
        if (typeof matrixDirected==="string") throw new Error(directed);
        let connected = isGraphConnected({matrix: matrixUndirected});
        if (typeof connected==="string") throw new Error(connected);
        if (connected) {
            let withCycles = hasCycles({matrix: matrixUndirected});
            if (typeof withCycles==="string") throw new Error(withCycles);
            result = !withCycles;
        }
    } catch(e){result = e.message}
    return result;
}

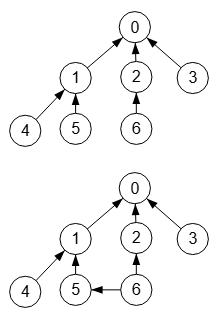
Aplicando direcciones arriba a la aristas, en el sentido hijo🡒padre tal como lo definimos en direccionalidad en grafos vemos que el primer grafo de la Figura sí es un árbol, mientras que el segundo no lo es. Los árboles dirigidos como el primero, con todas las flechas descendentes que parten de un nodo raíz o ascendentes que llevan a la raíz se les denomina grafos arborescentes y son árboles, pues sus versiones no dirigidas son árboles. Pero en caso de que su versión no dirigida tenga ciclos como el segundo de la Figura no es un árbol. A no ser que se consideren otros criterios, como veremos a continuación.

Es el grafo una arborescencia `isGraphArborescence()`

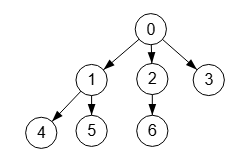
Un grafo dirigido especificando un nodo raíz es una arborescencia si desde ese nodo raíz sólo hay un único camino posible a cada uno de los nodos restantes. El grafo de la Figura es una arborescencia para el nodo raíz "0".

Vea que este criterio es distinto del que vimos con isGraphTree() del apartado anterior para grafos dirigidos, pues ahora especificamos un nodo raíz y la obligatoriedad de que exista un único camino entre la raíz y cada uno de los nodos restantes.

{"nodes":[
    {"index":0,"nodeOffset":"10.33 -0.8","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"11.64 -5.4","parent":[{"index":0}]},
    {"index":2,"nodeOffset":"10.93 -5.8","parent":[{"index":0}]},
    {"index":3,"nodeOffset":"8.5 -5.4","parent":[{"index":0}]},
    {"index":4,"nodeOffset":"-8.5 -9.2","parent":[{"index":1}]},
    {"index":5,"nodeOffset":"-13.36 -10","parent":[{"index":1}]},
    {"index":6,"nodeOffset":"-14.07 -10","parent":[{"index":2}]}
],
"config":{
    "markerStart":"arrow",
    "algorithm":"Is graph arborescence"
}}

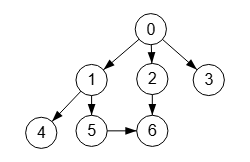
El grafo de la Figura con el nodo raíz "0" no es una arborescencia, pues desde ahí podemos llegar al nodo "6" por dos caminos, uno es "0🡒1🡒5🡒6" y otro "0🡒2🡒6".

{"nodes":[
    {"index":0,"nodeOffset":"10.33 -0.8","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"11.64 -5.4","parent":[{"index":0}]},
    {"index":2,"nodeOffset":"10.93 -5.8","parent":[{"index":0}]},
    {"index":3,"nodeOffset":"8.5 -5.4","parent":[{"index":0}]},
    {"index":4,"nodeOffset":"-8.5 -9.2","parent":[{"index":1}]},
    {"index":5,"nodeOffset":"-13.36 -10","parent":[{"index":1},{"index":6,"markerStart":"none","markerEnd":"arrow"}]},
    {"index":6,"nodeOffset":"-14.07 -10","parent":[{"index":2}]}
],
"config":{
    "markerStart":"arrow",
    "algorithm":"Is graph arborescence"
}}

En las opciones de la Figura vemos la única opción raíz para seleccionar el nodo raíz de la arborescencia.

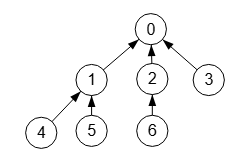
El grafo de la Figura es un árbol siguiendo el criterio de isGraphTree(), pero no es una arborescencia con isGraphArborescence() para ningún nodo actuando como raíz.

{"nodes":[
    {"index":0,"nodeOffset":"10.33 -0.8","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"11.64 -5.4","parent":[{"index":0}]},
    {"index":2,"nodeOffset":"10.93 -5.8","parent":[{"index":0}]},
    {"index":3,"nodeOffset":"8.5 -5.4","parent":[{"index":0}]},
    {"index":4,"nodeOffset":"-8.5 -9.2","parent":[{"index":1}]},
    {"index":5,"nodeOffset":"-13.36 -10","parent":[{"index":1}]},
    {"index":6,"nodeOffset":"-14.07 -10","parent":[{"index":2}]}
],
"config":{
    "markerEnd":"arrow",
    "algorithm":"Is graph arborescence"
}}

A continuación vemos el JavaScript del algoritmo isGraphArborescence(), usando isGraphDirected() para saber si el grafo es dirigido.También usa findPath() para encontrar todos los caminos entre el nodo raíz y el resto de nodos, comprobando que sólo haya un camino.

function isGraphArborescence({matrix=[], root=-1}){
    let result = false, temp;
    try {
        let n = matrix.length;
        if (temp = isGraphDirected({matrix}), typeof temp==="string") throw new Error(temp);
        let directed = temp;
        if (!directed){
            throw new Error(`isGraphArborescence() does not apply to undirected graphs`)
        } else if (root<0 || root>=n) {
            throw new Error(`Root '${root} is wrong`)
        } else {
            for (let i=0; i<n; i++) {
                if (i!==root) {
                    if (temp = findPath({matrix, firstIndex:root, lastIndex:i, findAll:true}), typeof temp==="string") throw new Error(temp);
                    let paths = temp;
                    if (paths.length===0 || paths.length>1) {
                        return false;
                    }
                }
            }
            return true;
        }
    } catch(e){result = e.message}
    return result;
}

Obtener componentes conectados getConnectedComponents()

Es el grafo conectado isGraphConnected()

Convertir a fuertemente conectado convertToStronglyConnected()

Es el grafo totalmente desconectado isGraphAllDisconnected()

Es el grafo un árbol isGraphTree()