Obtener subgrafo inducido getInducedSubgraph()

En un grafo con n nodos definimos un subgrafo inducido al grafo resultante compuesto con k ≤ n nodos y todas sus aristas incidentes.

Obtener subgrafo
inducido:
[[0,0,0,1,0,0],
[0,0,1,0,1,0],
[0,1,0,0,0,1],
[1,0,0,0,1,1],
[0,1,0,1,0,0],
[0,0,1,1,0,0]]

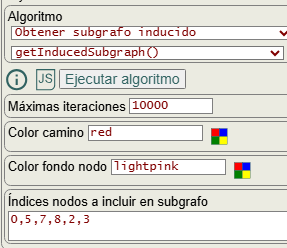
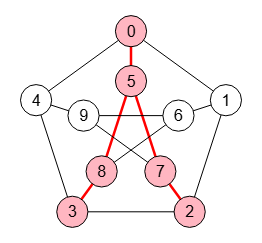
Por ejemplo, en la Figura vemos el grafo de Petersen con el subgrafo inducido con la lista de nodos "0,5,7,8,2,3" y las aristas que inciden entre ellos. La aplicación devuelve la matriz de adyacencia del subgrafo inducido por esos nodos.

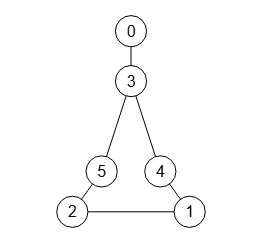
Importando la matriz de adyacencia del subgrafo obtenido y posicionando los nodos, observamos en la Figura ese subgrafo, donde no se conservan los títulos de los nodos, pues esto no es posible trasladarlo en la matriz de adyacencia. En cambio se trasladan los valores de las aristas, como veremos más abajo. En cualquier caso se mantiene una correspondencia entre "0,2,3,5,7,8" ordenados creciente en el grafo original y "0,1,2,3,4,5" en el subgrafo.

Para posicionar los nodos usamos el ajuste visual para posicionar copiando las ubicaciones de los nodos "0,2,3,5,7,8" del grafo original y trasladándolas al subgrafo de la Figura.

Este es el JSON del subgrafo posicionado:

{"nodes":[
    {"index":0,"nodeOffset":"19.17","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"9.34 72.36","parent":[{"index":-1}]},
    {"index":2,"nodeOffset":"3.99 47.36","parent":[{"index":1}]},
    {"index":3,"nodeOffset":"2.5 -5","parent":[{"index":0}]},
    {"index":4,"nodeOffset":"-10.74 31.18","parent":[{"index":1},{"index":3}]},
    {"index":5,"nodeOffset":"-9.26 6.18","parent":[{"index":2},{"index":3}]}
],
"config":{}}

Y este es el JSON del ejemplo.

{"nodes":[
    {"index":0,"nodeOffset":"2.5","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"65.54 2.64","parent":[{"index":0}]},
    {"index":2,"nodeOffset":"51.01 22.36","parent":[{"index":1}]},
    {"index":3,"nodeOffset":"-4.34 -2.64","parent":[{"index":2}]},
    {"index":4,"nodeOffset":"-35.54 2.64","parent":[{"index":0},{"index":3}]},
    {"index":5,"nodeOffset":"-22.5 -5","parent":[{"index":0}]},
    {"index":6,"nodeOffset":"21.52 -16.18","parent":[{"index":1}]},
    {"index":7,"nodeOffset":"-2.41 -18.82","parent":[{"index":2},{"index":5}]},
    {"index":8,"nodeOffset":"-9.26 -43.82","parent":[{"index":3},{"index":5},{"index":6}]},
    {"index":9,"nodeOffset":"-41.52 -16.18","parent":[{"index":4},{"index":6},{"index":7}]}
],
"config":{
    "algorithm":"Get induced subgraph",
    "indexesSubgraph":"0,5,7,8,2,3"
}}

En la Figura vemos las opciones para ejecutar el algoritmo. En índices de nodos a incluir en subgrafo relacionamos los nodos a extraer. El color camino y color fondo nodo no se pasan al algoritmo y sólo sirven para resaltar posteriormente los nodos y aristas del subgrafo.

Obtener subgrafo
inducido:
[[0,0,0,10,0,0],
[0,0,15,0,13,0],
[0,15,0,0,0,14],
[10,0,0,0,11,12],
[0,13,0,11,0,0],
[0,0,14,12,0,0]]

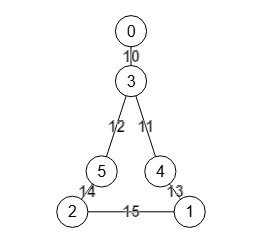
En la Figura vemos el mismo grafo de Petersen con aristas etiquetadas, siendo un grafo ponderado, observando en la Figura que el subgrafo inducido por los nodos "0,5,7,8,2,3" conserva esas etiquetas, aunque no las de los nodos como dijimos antes.

La obtención del subgrafo siempre se ejecuta en modo valores 0/1 o 0/number, convirtiendo las aristas de los modos null/value y false/true en modo 0/1.

A continuación se exponen los JSON de los dos grafos anteriores.

{"nodes":[
    {"index":0,"nodeOffset":"2.5","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"65.54 2.64","parent":[{"index":0,"value":1}]},
    {"index":2,"nodeOffset":"51.01 22.36","parent":[{"index":1,"value":6}]},
    {"index":3,"nodeOffset":"-4.34 -2.64","parent":[{"index":2,"value":15}]},
    {"index":4,"nodeOffset":"-35.54 2.64","parent":[{"index":0,"value":2},{"index":3,"value":9}]},
    {"index":5,"nodeOffset":"-22.5 -5","parent":[{"index":0,"value":10}]},
    {"index":6,"nodeOffset":"21.52 -16.18","parent":[{"index":1,"value":3}]},
    {"index":7,"nodeOffset":"-2.41 -18.82","parent":[{"index":2,"value":13},{"index":5,"value":11}]},
    {"index":8,"nodeOffset":"-9.26 -43.82","parent":[{"index":3,"value":14},{"index":5,"value":12},{"index":6,"value":7}]},
    {"index":9,"nodeOffset":"-41.52 -16.18","parent":[{"index":4,"value":5},{"index":6,"value":4},{"index":7,"value":8}]}
],
"config":{
    "algorithm":"Get induced subgraph",
    "indexesSubgraph":"0,5,7,8,2,3"
}}

{"nodes":[
    {"index":0,"nodeOffset":"19.17","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"9.34 72.36","parent":[{"index":-1}]},
    {"index":2,"nodeOffset":"3.99 47.36","parent":[{"index":1,"value":15}]},
    {"index":3,"nodeOffset":"2.5 -5","parent":[{"index":0,"value":10}]},
    {"index":4,"nodeOffset":"-10.74 31.18","parent":[{"index":1,"value":13},{"index":3,"value":11}]},
    {"index":5,"nodeOffset":"-9.26 6.18","parent":[{"index":2,"value":14},{"index":3,"value":12}]}
],
"config":{}}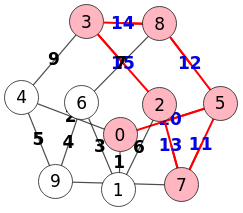

En Wolfram con Subgraph de la forma Subgraph[g, {v1, v2, ...} obtenemos el subgrafo inducido por una lista de vértices, tal como vemos en la Figura para los vértices "0,2,3,5,7,8" que en Wolfram pasamos como {1,3,4,6,8,9} pues los índices se inician en 1. Aunque algunos elementos se solapan visualmente, se obtiene el mismo resultado.

En el código siguiente se observa que para el grafo ponderado usamos WeightedAdjacencyGraph aplicado sobre la matriz de adyacencia en modo "0/number" cambiando "0" por "∞". En otro caso se aplica AdjacencyGraph con la matriz de adyacencia en modo "0/1". El resto es igual para ambos casos.

g = WeightedAdjacencyGraph[{{∞,1,∞,∞,2,10,∞,∞,∞,∞},{1,∞,6,∞,∞,∞,3,∞,∞,∞},{∞,6,∞,15,∞,∞,∞,13,∞,∞},{∞,∞,15,∞,9,∞,∞,∞,14,∞},{2,∞,∞,9,∞,∞,∞,∞,∞,5},
{10,∞,∞,∞,∞,∞,∞,11,12,∞},{∞,3,∞,∞,∞,∞,∞,∞,7,4},{∞,∞,13,∞,∞,11,∞,∞,∞,8},{∞,∞,∞,14,∞,12,7,∞,∞,∞},{∞,∞,∞,∞,5,∞,4,8,∞,∞}}, ImageSize -> 243, 
VertexSize -> {"Scaled", 0.13}, VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center], 3 -> Placed[2,Center], 4 -> Placed[3,Center], 
5 -> Placed[4,Center], 6 -> Placed[5,Center], 7 -> Placed[6,Center], 8 -> Placed[7,Center], 9 -> Placed[8,Center], 10 -> Placed[9,Center]}, 
VertexLabelStyle -> Directive[Black,17.5], EdgeLabelStyle -> Directive[Black,17.5,Bold], EdgeLabels -> {(2->1)->1, (3->2)->6, (4->3)->15, 
(5->1)->2, (5->4)->9, (6->1)->10, (7->2)->3, (8->3)->13, (8->6)->11, (9->4)->14, (9->6)->12, (9->7)->7, 
(10->5)->5, (10->7)->4, (10->8)->8}, VertexStyle -> White, EdgeStyle -> {{Black,Thickness[0.005]}}];
Subgraph[g, {1,3,4,6,8,9}];
HighlightGraph[g,{Style[VertexList[%], RGBColor["lightpink"]], Style[EdgeList[%], Red, Thick], Annotation[EdgeList[%], EdgeLabelStyle->Directive[Blue,17.5,Bold]]}]

El JavaScript del algoritmo getInducedSubgraph() es muy simple. Iteramos por todos los nodos del grafo filtrando los que se pasen en indexesSubgraph y con otro bucle buscamos las aristas incidentes para ir construyendo la matriz del resultado del subgrafo.

function getInducedSubgraph({matrix=[], indexesSubgraph=[]}){
    let result = [];
    try {
        let n = matrix.length;
        for (let i=0; i<n; i++) {
            if (indexesSubgraph.includes(i)) {
                let arr = [];
                for (let j=0; j<n; j++) {
                    if (indexesSubgraph.includes(j)){
                        arr.push(matrix[i][j])
                    }
                }
                result.push(arr);
            }
        }
    } catch(e){result = e.message}
    return result;
}

Obtener subgrafo getSubgraph()

En un grafo con n nodos definimos un subgrafo al subgrafo inducido resultante compuesto con k ≤ n nodos y todas sus aristas incidentes tras lo cual eliminamos cero o más aristas. En caso de no eliminar ninguna el subgrafo será un inducido, como vimos en el apartado anterior.

Obtener subgrafo: 
[[0,0,0,1,0,0],
[0,0,0,0,1,0],
[0,0,0,0,0,1],
[1,0,0,0,1,1],
[0,1,0,1,0,0],
[0,0,1,1,0,0]]

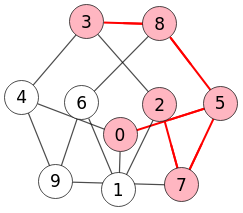
En la Figura vemos un subgrafo obtenido con el inducido por los nodos "0,5,7,8,2,3" tras lo cual eliminamos la arista [2,3].

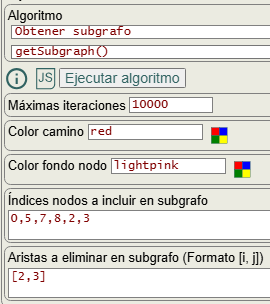
En la Figura vemos las opciones para ejecutar el algoritmo. La opción índices nodos a incluir en subgrafo es el mismo que vimos en el apartado anterior para obtener el subgrafo inducido por esos nodos. Con la opción aristas a eliminar en subgrafo (Formato [i,j]) se incluyen las aristas que se eliminarán tras crear el subgrafo inducido. El formato [i,j] son para aristas no dirigidas "i-j" o para dirigidas "i🡒j".

Las opciones color camino y color fondo nodo no forman parte del algoritmo y se aplican posteriormente para resaltar nodos y aristas del subgrafo en el grafo.

{"nodes":[
    {"index":0,"nodeOffset":"2.5","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"65.54 2.64","parent":[{"index":0}]},
    {"index":2,"nodeOffset":"51.01 22.36","parent":[{"index":1}]},
    {"index":3,"nodeOffset":"-4.34 -2.64","parent":[{"index":2}]},
    {"index":4,"nodeOffset":"-35.54 2.64","parent":[{"index":0},{"index":3}]},
    {"index":5,"nodeOffset":"-22.5 -5","parent":[{"index":0}]},
    {"index":6,"nodeOffset":"21.52 -16.18","parent":[{"index":1}]},
    {"index":7,"nodeOffset":"-2.41 -18.82","parent":[{"index":2},{"index":5}]},
    {"index":8,"nodeOffset":"-9.26 -43.82","parent":[{"index":3},{"index":5},{"index":6}]},
    {"index":9,"nodeOffset":"-41.52 -16.18","parent":[{"index":4},{"index":6},{"index":7}]}
],
"config":{
    "algorithm":"Get subgraph",
    "indexesSubgraph":"0,5,7,8,2,3",
    "deleteEdgesSubgraph":"[2,3]"
}}

En Wolfram aplicamos Subgraph con Subgraph[g, {v1, v2, ...} obteniéndose el subgrafo inducido con esos vértices y luego borramos aristas con EdgeDelete aplicando EdgeDelete[g, {e1, e2, ...}], quedando en la Figura como Subgraph[g, {1,3,4,6,8,9}] y EdgeDelete[%, {3<->4}] borrándose la arista entre los nodos "2" y "3" con nuestros índices.

También es posible Subgraph[g, {e1, e2, ...}] donde se especifican las aristas que forman parte del subgrafo, pudiendo usarse Subgraph[g, {4<->9, 9<->6, 6<->1, 6<->8, 8<->3}] para lo mismo, pero preferimos la forma anterior pues hace lo mismo que ejecutamos en la aplicación: obtener subgrafo inducido y eliminar una o más aristas del subgrafo.

g = AdjacencyGraph[{{0,1,0,0,1,1,0,0,0,0},{1,0,1,0,0,0,1,0,0,0},{0,1,0,1,0,0,0,1,0,0},{0,0,1,0,1,0,0,0,1,0},{1,0,0,1,0,0,0,0,0,1},
{1,0,0,0,0,0,0,1,1,0},{0,1,0,0,0,0,0,0,1,1},{0,0,1,0,0,1,0,0,0,1},{0,0,0,1,0,1,1,0,0,0},{0,0,0,0,1,0,1,1,0,0}}, ImageSize -> 243, 
VertexSize -> {"Scaled", 0.13}, VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center], 3 -> Placed[2,Center], 4 -> Placed[3,Center], 
5 -> Placed[4,Center], 6 -> Placed[5,Center], 7 -> Placed[6,Center], 8 -> Placed[7,Center], 9 -> Placed[8,Center], 10 -> Placed[9,Center]}, 
VertexLabelStyle -> Directive[Black,17.5], EdgeLabelStyle -> Directive[Black,17.5,Bold], VertexStyle -> White, EdgeStyle -> {{Black,Thickness[0.005]}}];
Subgraph[g, {1,3,4,6,8,9}];
EdgeDelete[%, {3<->4}];
HighlightGraph[g,{Style[VertexList[%], RGBColor["lightpink"]], Style[EdgeList[%], Red, Thick], Annotation[EdgeList[%], EdgeLabelStyle->Directive[Blue,17.5,Bold]]}]

El JavaScript del algoritmo getSubgraph() se expone a continuación, donde obtenemos el subgrafo inducido con el algoritmo getInducedSubgraph() que vimos en el apartado anterior. Hacemos uso de isGraphDirected() para saber si el grafo es dirigido, pues de no serlo cuando eliminemos la arista no dirigida "u-v" tendremos que borrar las posiciones [u][v] y [v][u] de la matriz de adyacencia del subgrafo que vamos a obtener.

function getSubgraph({matrix=[], indexesSubgraph=[], deleteEdgesSubgraph=[], directed=null}){
    let result = [];
    try {
        if (directed===null) {
            directed = isGraphDirected({matrix});
            if (typeof directed==="string") throw new Error(directed);
        }
        let induced = getInducedSubgraph({matrix, indexesSubgraph});
        if (typeof induced==="string") throw new Error(induced);
        for (let edge of deleteEdgesSubgraph) {
            let [i, j] = edge;
            let ii = indexesSubgraph.indexOf(i);
            let jj = indexesSubgraph.indexOf(j);
            if (ii>-1 && jj>-1) {
                induced[ii][jj] = 0;
                if (!directed) induced[jj][ii] = 0;
            }
        }
        result = induced;
    } catch(e){result = e.message}
    return result;
}

Obtener subgrafo recubridor getSpanningSubgraph()

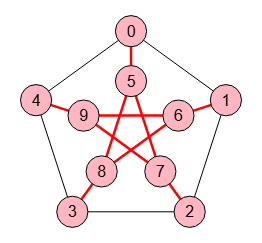
En un grafo con n nodos definimos un subgrafo recubridor al que contiene todos los n nodos y sólo algunas aristas del grafo original. Si las contiene todas ambos son iguales.

Obtener subgrafo
recubridor:
[[0,0,0,0,0,1,0,0,0,0],
[0,0,0,0,0,0,1,0,0,0],
[0,0,0,0,0,0,0,1,0,0],
[0,0,0,0,0,0,0,0,1,0],
[0,0,0,0,0,0,0,0,0,1],
[1,0,0,0,0,0,0,1,1,0],
[0,1,0,0,0,0,0,0,1,1],
[0,0,1,0,0,1,0,0,0,1],
[0,0,0,1,0,1,1,0,0,0],
[0,0,0,0,1,0,1,1,0,0]]

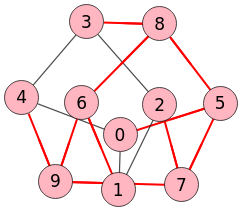
En la Figura vemos el subgrafo recubridor que contiene todos los nodos del grafo original y al que le hemos quitado las aristas exteriores.

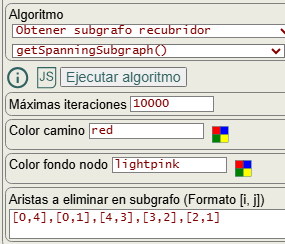
En la Figura vemos las opciones para ejecutar el algoritmo. La opción aristas a eliminar en subgrafo (Formato [i,j]) se incluyen las aristas que se eliminarán de una copia del grafo original que pasará a ser un subgrafo recubridor. El formato [i,j] son para aristas no dirigidas "i-j" o para dirigidas "i🡒j".

Las opciones color camino y color fondo nodo no forman parte del algoritmo y se aplican posteriormente para resaltar nodos y aristas del subgrafo en el grafo.

{"nodes":[
    {"index":0,"nodeOffset":"2.5","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"65.54 2.64","parent":[{"index":0}]},
    {"index":2,"nodeOffset":"51.01 22.36","parent":[{"index":1}]},
    {"index":3,"nodeOffset":"-4.34 -2.64","parent":[{"index":2}]},
    {"index":4,"nodeOffset":"-35.54 2.64","parent":[{"index":0},{"index":3}]},
    {"index":5,"nodeOffset":"-22.5 -5","parent":[{"index":0}]},
    {"index":6,"nodeOffset":"21.52 -16.18","parent":[{"index":1}]},
    {"index":7,"nodeOffset":"-2.41 -18.82","parent":[{"index":2},{"index":5}]},
    {"index":8,"nodeOffset":"-9.26 -43.82","parent":[{"index":3},{"index":5},{"index":6}]},
    {"index":9,"nodeOffset":"-41.52 -16.18","parent":[{"index":4},{"index":6},{"index":7}]}
],
"config":{
    "algorithm":"Get spanning subgraph",
    "deleteEdgesSubgraph":"[0,4],[0,1],[4,3],[3,2],[2,1]"
}}

En Wolfram aplicamos Subgraph con Subgraph[g, {v1, v2, ...} obteniéndose el subgrafo inducido con todos los vértices del grafo original y luego borramos aristas con EdgeDelete aplicando EdgeDelete[g, {e1, e2, ...}], quedando en la Figura como Subgraph[g, {1,2,3,4,5,6,7,8,9,10}] y EdgeDelete[%, {1<->5,1<->2,5<->4,4<->3,3<->2}]; borrándose las aristas "0-4, 0-1, 4-3, 3-2, 2-1" con los índices de nuestra aplicación.

También es posible Subgraph[g, {e1, e2, ...}] donde se especifican las aristas que forman parte del subgrafo, pudiendo especificar las aristas que quedan para lo mismo, pero preferimos la forma anterior pues hace lo mismo que ejecutamos en la aplicación: copiar el grafo original y eliminar una o más aristas del subgrafo.

g = AdjacencyGraph[{{0,1,0,0,1,1,0,0,0,0},{1,0,1,0,0,0,1,0,0,0},{0,1,0,1,0,0,0,1,0,0},{0,0,1,0,1,0,0,0,1,0},{1,0,0,1,0,0,0,0,0,1},{1,0,0,0,0,0,0,1,1,0},
{0,1,0,0,0,0,0,0,1,1},{0,0,1,0,0,1,0,0,0,1},{0,0,0,1,0,1,1,0,0,0},{0,0,0,0,1,0,1,1,0,0}}, ImageSize -> 243, VertexSize -> {"Scaled", 0.13}, 
VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center], 3 -> Placed[2,Center], 4 -> Placed[3,Center], 5 -> Placed[4,Center], 
6 -> Placed[5,Center], 7 -> Placed[6,Center], 8 -> Placed[7,Center], 9 -> Placed[8,Center], 10 -> Placed[9,Center]}, 
VertexLabelStyle -> Directive[Black,17.5], EdgeLabelStyle -> Directive[Black,17.5,Bold], VertexStyle -> White, EdgeStyle -> {{Black,Thickness[0.005]}}];
Subgraph[g, {1,2,3,4,5,6,7,8,9,10}];
EdgeDelete[%, {1<->5,1<->2,5<->4,4<->3,3<->2}];
HighlightGraph[g,{Style[VertexList[%], RGBColor["lightpink"]], Style[EdgeList[%], Red, Thick], Annotation[EdgeList[%], EdgeLabelStyle->Directive[Blue,17.5,Bold]]}]

A continuación vemos el JavaScript del algoritmo getSpanningSubgraph(), donde hacemos una copia del grafo original y luego borramos aristas. Hacemos uso de isGraphDirected() para saber si el grafo es dirigido, pues de no serlo lo fuera cuando eliminemos la arista no dirigida "u-v" tendremos que borrar las posiciones [u][v] y [v][u] de la matriz de adyacencia del subgrafo que vamos a obtener.

function getSpanningSubgraph({matrix=[], deleteEdgesSubgraph=[], directed=null}){
    let result = [];
    try {
        if (directed===null) {
            directed = isGraphDirected({matrix});
            if (typeof directed==="string") throw new Error(directed);
        }
        result = JSON.parse(JSON.stringify(matrix));
        for (let edge of deleteEdgesSubgraph) {
            let [i, j] = edge;
            result[i][j] = 0;
            if (!directed) result[j][i] = 0;
        }
    } catch(e){result = e.message}
    return result;
}