Algoritmos de Kruskal y Prim
Árboles de recubrimiento mínimo
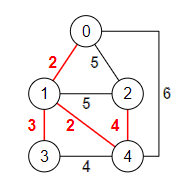
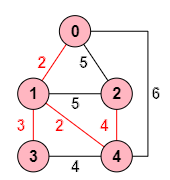
Un problema donde aplicar el algoritmo voraz es el de obtener el árbol de recubrimiento mínimo en un grafo conexo no dirigido, como el de la Figura. Ese árbol es un subgrafo que conecta todos los nodos siguiendo un camino cuyo coste de la suma del valor de las aristas es mínimo. En la Figura se representa con las aristas en color rojo.
El subgrafo obtenido contiene los 5 nodos del grafo unidos por 4 aristas. Hay que recordar que un grafo conexo con n nodos debe contener al menos n-1 aristas. Si contiene menos no es conexo. Si contiene más existe al menos un ciclo. En otro caso si contiene exactamente n-1 aristas ese subgrafo es un árbol pues es conexo y no contiene ciclos.
Este planteamiento se aplica en problemas reales. Supongamos que cada nodo representa una ciudad y queremos tender un cable teléfonico que conecte todas las ciudades usando la menor longitud de cable. Los valores de las aristas son las distancias entre ciudades pasando por lugares por donde podríamos instalar ese cable, como carreteras. Buscando el árbol de recubrimiento mínimo obtendríamos la menor distancia que conecta todas las ciudades.
Algoritmo voraz para el árbol de recubrimiento mínimo
El algoritmo voraz es el que necesitamos para resolver este problema de optimización. Recordemos como era el algoritmo básico:
function voraz(conjunto){
let resultado = crear(conjunto);
while (!esSolucion(resultado) && !esVacio(conjunto)){
let candidato = seleccionar(conjunto);
if (esCompletable(resultado, candidato)) {
resultado = guardar(resultado, candidato);
}
}
return resultado;
}Como conjunto formaríamos un array con las aristas ordenadas por su valor ascendente. El bucle voraz consistiría en iterar por ese array. La función seleccionar candidato está ya implícita en el ordenamiento del array, pues en cada iteración tomamos la arista de menor valor. Esta selección permitirá alcanzar la función objetivo que es obtener las n-1 aristas que, con una suma mínima, consiga conectar los n nodos del grafo y no contenga ciclos. Es decir, consigamos el árbol de los n nodos cuya suma de aristas es mínima. Para ver si la selección de una arista es completable hemos de comprobar si una arista que se agregue al resultado formará un árbol.
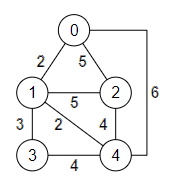
Veamos paso a paso como construir el árbol de recubrimiento mínimo del grafo de la Figura. Empezamos por construir un array con las aristas en orden ascendente por su valor:
["1,0", "4,1", "3,1", "3,4", "4,2", "2,0", "2,1", "4,0"]Cada arista i, j une los nodos con índices i y j. Ahora iteraremos por ese array considerando cada arista para incorporarla al árbol de recubrimiento mínimo.
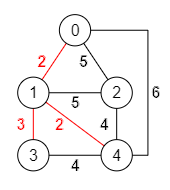
El grafo tiene en total ocho aristas. El árbol de recubrimiento mínimo tendrá cuatro aristas, uno menos que el número de nodos del grafo. Esas cuatro deben estar entre las primeras del array, pues se han ordenado por orden creciente de valor. Pero no tienen porque ser necesariamente las cuatro primeras del array. El subgrafo formado por las tres primeras aristas "1,0", "4,1", "3,1" forma un árbol válido, como vemos en la Figura señalado en rojo. Es un árbol porque conecta los nodos 0, 1, 3, 4 y no tiene ciclos.
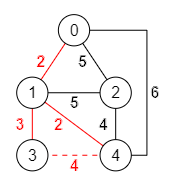
Al tratar de agregar la cuarta arista "3,4" del array se formará un ciclo, como vemos en la Figura con la línea discontinua roja. Por lo tanto esa arista se descarta.
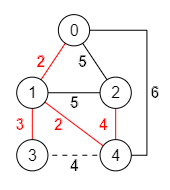
Tomamos la siguiente arista "4,2" del array y vemos que no forma ciclos. Ya tenemos cuatro aristas, uno menos que el número de nodos. Hemos finalizado obteniendo el árbol de recubrimiento mínimo.
Hasta aquí es como lo haríamos de una forma "manual". Veamos como se implementa en el algoritmo voraz la solución al problema de comprobar si se forma un ciclo al intentar construir el árbol de recubrimiento mínimo.
El algoritmo de Kruskal
getMinimumSpanningTreeKruskal(), como el que se expone aquí con algunas mejoras.Para ver si la selección de una arista es completable hemos de comprobar si una arista que se agregue al resultado formará un árbol. Para conseguirlo aplicaremos la particularidad del algoritmo de Kruskal, que se basa en usar una estructura de partición o de conjuntos disjuntos.
Antes de exponer el código hemos de decir que usamos una estructura para representar un grafo tal como se expone en la herramienta Web Tools online: Grafos. Para el grafo de ejemplo que hemos estado usando en los apartados anteriores, la estructura es la siguiente:
[{"index":0, "parent":-1},
{"index":1, "parent":
[{"index":0, "value":2}]
},
{"index":2, "parent":
[{"index":0, "value":5},
{"index":1, "value":5}]
},
{"index":3, "parent":
[{"index":1, "value":3},
{"index":4, "value":4}]
},
{"index":4, "parent":
[{"index":1, "value":2},
{"index":2, "value":4},
{"index":0, "value":6}]
}]Cada nodo se identifica con un índice index. Aunque en la herramienta para editar grafos se permiten índices enteros no negativos cualesquiera, no necesariamente correlativos, para aplicar la estructura de partición necesitamos que sean correlativos empezando en cero.
Cada nodo tiene obligatoriamente uno o más enlaces que configuran aristas a otros nodos. Estos enlaces se incluyen en un array en parent. Uno de los nodos es el inicial y le asignamos -1. Para el resto configuramos los enlaces sin tener en cuenta el sentido del enlace en el caso de que querramos un grafo no dirigido, como es el caso. El valor de la arista se indica en value. Pueden incluirse otras propiedades opcionales como lineOffset o lineTextOffset que sirven para la presentación visual del grafo, no interviniendo en la estructura básica que necesitamos para este caso.
Conocido lo anterior veamos ahora la implementación en JavaScript del algoritmo de Kruskal.
function kruskal(nodos=[]){
let aristas = {};
for (let nodo of nodos){
if (Array.isArray(nodo.parent)){
for (let link of nodo.parent){
if (typeof link==="object" && link.hasOwnProperty("value")){
aristas[`${nodo.index},${link.index}`] = link.value;
}
}
}
}
let aristasEnOrden = Object.keys(aristas).sort((a,b) => aristas[a]-aristas[b]);
let conjuntosIniciales = nodos.map(v => [v.index]);
let [rotulos, rangos, elementos] = construir(conjuntosIniciales);
let rotulo1, rotulo2;
let resultado = [];
for (let arista of aristasEnOrden){
let [index1, index2] = arista.split(/,/).map(v => +v);
[rotulo1, rotulos] = buscar(rotulos, index1);
[rotulo2, rotulos] = buscar(rotulos, index2);
if (rotulo1 !== rotulo2){
[rotulos, rangos] = fusionar(rotulos, rangos, rotulo1, rotulo2);
resultado.push(arista);
if (resultado.length === nodos.length-1) break;
}
}
return resultado;
}Recibimos el argumento nodos con la estructura que vimos antes. Extraemos las aristas iterando por los nodos y su propiedad parent. El objeto aristas contiene las claves de la forma "a,b" donde "a" y "b" son índices de nodos. Cada propiedad de ese objeto guardará el valor de la arista. Esto nos permite ordenarlas por valor creciente y guardarlas en aristasEnOrden.
El siguiente paso es construir la estructura de partición. Los conjuntos iniciales serán los nodos, con lo que usando la función construir(conjuntosIniciales) obtenemos los rotulos y rangos que necesitaremos para manejar la partición. También obtenemos elementos, pero para esta aplicación no se necesitará.
Declaramos la variable resultado, un array que contendrá las aristas que finalmente seleccione el voraz. Y empezamos ahora con el bucle voraz que itera por el array de aristas en orden. Veamos el ejemplo interactivo y luego explicaremos paso a paso el funcionamiento del ejemplo que se carga con el botón titulado "Ejemplo 1".
Ejemplo: Algoritmo de Kruskal: árbol de recubrimiento mínimo
kruskal(grafo): 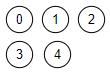
Antes de entrar en el bucle construimos una partición con los 5 conjuntos disjuntos, uno para cada nodo, tal como se observa en Figura. Es la representación gráfica en forma de árboles de la estructura de partición. No debe confudirse con el grafo sobre el que estamos descubriendo su árbol de recubrimiento mínimo.
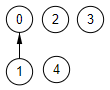
Recordemos que el bucle voraz itera por el array de aristas ["1,0","4,1","3,1","3,4","4,2","2,0","2,1","4,0"] que están ordenadas crecientes por el valor de la arista. Empezamos el bucle con la primera arista "1,0". Es la arista que une los nodos con índices index1 = 1, index2 = 0. Buscamos los rótulos de los conjuntos disjuntos donde se encuentran esos índices en la estructura de partición, coincidiendo con esos índices. Entonces como rotulo1 !== rotulo2 fusionamos ambos disjuntos y agregamos la arista "1,0" al resultado. La estructura de partición finaliza como se observa en la Figura.
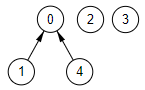
Pasamos a la siguiente arista "4,1". Están en dos disjuntos distintos con rótulos 4 y 0 respectivamente. Al estar en disjuntos distintos fusionamos disjuntos y agregamos arista al resultado. La partición queda como se ve en la Figura.
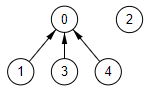
La siguiente arista "3,1" también está en dos disjuntos distintos con rótulos 3 y 0 respectivamente. Fusionamos y agregamos arista al resultado. La partición queda como se observa en la Figura.
A continuación viene la arista "3,4". Ambos nodos 3 y 4 están en el mismo disjunto con rótulo 0. Entonces como rotulo1===rotulo2 desechamos esa arista. Al estar ambos nodos en el mismo disjunto quiere decir que no puede agregarse esta arista pues formaríamos un ciclo.
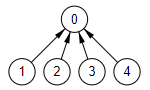
La siguiente arista es la "4,2", cuyos nodos 4 y 2 están en los disjuntos con rótulos 0 y 2 respectivamente. Son distintos y por tanto fusionamos y agregamos la arista al resultado. La partición queda como se ve en la Figura. Ya tenemos 4 aristas en el resultado y finalizamos saliendo del bucle. Observe como también los 5 conjuntos disjuntos que había incialmente en la partición se han fusionado en un único conjunto y no quedan más por fusionar.
La demostración de optimalidad es algo extensa para exponerla aquí. Se expone en la referencia Fundamentos de Algoritmia de G.Brassard, P.Bratley ya comentada.
Analizando el coste del algoritmo de Kruskal
En un grafo con a aristas y n nodos, el coste asintótico es O(a log n). Veamos el motivo de este resultado por cada parte del algoritmo.
La obtención de las aristas supone iterar por n nodos. Por cada nodo luego hay que iterar por sus enlaces a otros nodos. Si todos los nodos están conectados habrán C(n, 2) = ½ n (n-1) aristas (combinaciones de n nodos tomados de dos en dos). El coste sería O(n3), dado que el total de iteraciones sería ∑(i=1..n) (C(n, 2)-i+1) = ½ n (n-1)2, puesto que podríamos considerar el primer nodo conectado con todos, el segundo con todos menos el primero pues esa arista ya se incluye en la anterior, etc.
Podríamos suponer que ya nos dan el array de aristas a la entrada de la función de Kruskal. De hecho se observa que pasando además un entero con el número de nodos, podemos obviar ese argumento nodos que no necesitaremos en la ejecución del algoritmo de Kruskal.
Vease que en el código usamos la funcion construir(conjutosIniciales) que está preparada para construir una partición con conjuntos disjuntos en cualquier estado de agrupamiento. Pero en esta aplicación los conjuntos al principio están en su estado inicial, es decir, cada elemento en un conjunto disjunto. Por lo tanto podríamos modificar el código para simplificarlo.
Con estas simplificaciones el código queda como sigue, sobre el que analizaremos el coste.
function kruskal(aristas=[], n=0){
let aristasEnOrden = Object.keys(aristas).sort((a,b) => aristas[a]-aristas[b]);
let rotulos = Array.from({length:n}, () => 0);
let rangos = Array.from({length:n}, () => 0);
let rotulo1, rotulo2;
let resultado = [];
for (let arista of aristasEnOrden){
let [index1, index2] = arista.split(/,/).map(v => +v);
[rotulo1, rotulos] = buscar(rotulos, index1);
[rotulo2, rotulos] = buscar(rotulos, index2);
if (rotulo1 !== rotulo2){
[rotulos, rangos] = fusionar(rotulos, rangos, rotulo1, rotulo2);
resultado.push(arista);
if (resultado.length === n-1) break;
}
}
return resultado;
}Ordenar las aristas tiene un coste O(a log a) que es el típico de ordenar un array de longitud a. Como el grafo es conexo a ≥ n-1. Ya vimos que el máximo número de aristas posibles es a ≤ C(n, 2) = ½ n (n-1)2. Con el mínimo número de aristas posibles tendremos un coste de O(a log(n-1)) ⇒ O(a log n). Con el máximo número de aristas posibles el coste será O(a log(½ n (n-1)2)) ⇒ O(a log n2) ⇒ O(a 2 log n) ⇒ O(a log n). Para comprobar que esta equivalencia es cierta, recuerde la regla del límite que dice:
Aplicándola a lo anterior limn→∞ (a log(½ n (n-1)2))/(a log n) = 3 ∈ ℝ+, comprobándose la corrección de O(a log n) para cualquier número de aristas a ordenar.
El coste de construir la partición es O(n) puesto que hay que inicializar un array de n rótulos y otro de n rangos.
El coste del bucle voraz se analiza por medio del coste de la partición. En el tema anterior vimos que partiendo de n conjuntos disjuntos, el coste para fusionar todos los disjuntos en un único conjunto es O(c α(c, n)), donde c=b+f, siendo b el total de llamadas a buscar y f≤n-1 el total de llamadas a fusionar.
El bucle itera por a aristas como máximo, por lo que se producen b = 2a llamadas a buscar en el peor caso. Las operaciones fusionar siempre serán f=n-1, que son las necesarias para fusionar n conjuntos disjuntos. Con c=b+f=2a+n-1 el coste de nuestra partición será esencialmente lineal en este c, es decir, O(c) ⇒ O(2a+n-1) ⇒ O(2a) dado que a≥n-1.
De los tres costes en secuencia O(a log n), O(n) y O(2a) el máximo es O(a log n) usando la versión simplificada del algoritmo de Kruskal.
Algoritmo de Prim
getMinimumSpanningTreePrim(), como el que se expone aquí con algunas mejoras.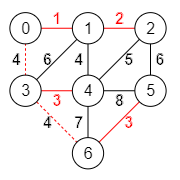
Con el algoritmo de Kruskal iterábamos por las aristas ordenadas por su valor creciente. Se iban formando subárboles no conectados entre sí a medida que avanzábamos por el bucle voraz. Si en el ejemplo interactivo del apartado anterior ejecuta el "Ejemplo 2", verá que en la iteración que selecciona la cuarta arista obtenemos el resultado parcial ["1,0", "2,1", "4,3", "6,5"]. Esto son tres subárboles no conectados como se muestra en la Figura marcados con línea continua en color rojo. Las aristas con línea de puntos son las que faltan para completar el árbol. Con ese algoritmo se van formando subárboles y al final todas las componentes se fusionan en un único árbol.
Otra forma de construir el árbol de recubrimiento mínimo es usando el algoritmo de Prim. En este caso no se ordenan las aristas. Vamos iterando por ellas haciendo una selección de proximidad a un nodo elegido, normalmente el primer nodo. A medida que el bucle voraz avanza, el árbol va creciendo de forma unificada hasta completar todos los nodos. Para el grafo anterior se van formando las aristas partiendo del nodo raíz 0. Cuando se agrega una nueva arista está conectada con alguna de las aristas ya existentes en el subárbol, como se muestra en la siguiente evolución del array de resultado:
i Resultado -------------------------------------- 1 ["1,0"] 2 ["1,0","2,1"] 3 ["1,0","2,1","3,0"] 4 ["1,0","2,1","3,0","4,3"] 5 ["1,0","2,1","3,0","4,3","6,3"] 6 ["1,0","2,1","3,0","4,3","6,3","5,6"]
El algoritmo teórico siguiente, un voraz, es el que se define para resolver el problema:
function prim(N=[]){
let resultado = []
let A = [];
while (A.length !== N.length){
let [x, y] = seleccionar(N, A);
A.push(y);
resultado.push(`${x},${y}`);
}
return resultado;
}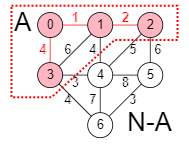
Supongamos que el argumento N es un array de nodos que define la estructura del grafo. Es el conjunto del algoritmo voraz sobre el que iteramos. El conjunto A contiene el árbol de recubrimiento mínimo que estamos formando. Para el ejemplo visto antes, en la Figura puede verlo para la iteración i=3. El conjunto N-A contiene los nodos que aún no se han agregado al árbol.
El bucle voraz finalizará cuando A contenga todos los nodos de N. La función para seleccionar un candidato es en este caso también completable. Al seleccionar un nodo, éste debe ya completar la solución. La selección debe obtener una arista formada por la pareja de nodos [x, y] de menor longitud, de tal forma que x ∈ A, y ∈ N-A. Agregamos el nodo y al conjunto A y la arista [x, y] al resultado.
Veamos una implementación práctica donde no es necesario declarar el conjunto A, aunque está implícito en la ejecución. El código del algoritmo y el ejemplo interactivo se exponene a continuación. Luego explicaremos paso a paso la ejecución.
function prim(nodes=[]){
let n = nodes.length;
let longitudesAristas = Array.from({length:n}, () =>
Array.from({length:n}, () => Infinity));
for (let node of nodes){
if (Array.isArray(node.parent)){
for (let link of node.parent){
if (typeof link==="object" && link.hasOwnProperty("value")){
longitudesAristas[node.index][link.index] = link.value;
longitudesAristas[link.index][node.index] = link.value;
}
}
}
}
let masProximo = [];
let distanciaMinima = [];
for (let i=0; i<n; i++){
masProximo[i] = 0;
distanciaMinima[i] = longitudesAristas[i][0];
}
let resultado = [];
for (let i=1; i<n; i++){
let minimo = Infinity;
let k;
for (let j=1; j<n; j++){
if (distanciaMinima[j]>=0 && distanciaMinima[j]<minimo){
minimo = distanciaMinima[j];
k = j;
}
}
resultado.push(`${k},${masProximo[k]}`);
distanciaMinima[k] = -1;
for (let j=1; j<n; j++){
if (longitudesAristas[j][k]<distanciaMinima[j]){
distanciaMinima[j] = longitudesAristas[j][k];
masProximo[j] = k;
}
}
}
return resultado;
}Ejemplo: Algoritmo de Prim: árbol de recubrimiento mínimo
prim(grafo): Veamos paso a paso como se ejecuta el "Ejemplo 1" que se observa en el ejemplo interactivo anterior.
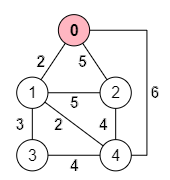
La función recibe como argumento el objeto nodos con la misma estructura que vimos en el apartado anterior. Para el algoritmo de Prim necesitamos un array de dimensión n×n que contenga los valores de las aristas. En el código creamos el array longitudesAristas suponiendo que los valores de las aristas representan longitudes. Aunque ese valor puede representar cualquier cosa, pensar en longitudes nos ayudará a entender mejor el algoritmo.
Con el grafo que puede ver en la Figura se genera el siguiente array de longitudes:
0 1 2 3 4 0 ∞ 2 5 ∞ 6 1 2 ∞ 5 3 2 2 5 5 ∞ ∞ 4 3 ∞ 3 ∞ ∞ 4 4 6 2 4 4 ∞
Tenemos los índices de los cinco nodos del grafo en la primera fila y primera columna, como cabeceras de fila y columna. Cada posición del array 5×5 representa la longitud de la arista que une cada pareja de nodos. Si no hay arista entre ellos se inserta el valor Infinity. La diagonal derecha, donde coinciden los nodos, también tiene este valor, dado que no se espera que un nodo pueda tener una arista que apunte a sí mismo (al menos en estos problemas). Este array se construye iterando por el objeto nodos.
Construimos otro array denominado masProximo que contendrá n posiciones. Si tenemos masProximo[i] = j significará que el nodo j será el que está más próximo al nodo i. Como seleccionamos siempre el nodo 0 como raíz, iniciamos con valores cero [0, 0, 0, 0, 0], de tal forma que inicialmente suponemos que es el nodo 0 el que está más próximo al resto de los nodos. Obviamente lo único cierto que sabemos es que el más próximo al nodo 0 es el propio 0, el resto lo iremos descubriendo a medida que avance el bucle voraz.
También necesitamos otro array también de longitud n. Con distanciaMinima[i] = d significará que d es la distancia desde el nodo i al más próximo j que se almacena en el array masProximo. Cuando un nodo se agrega al árbol que vamos formado, le ponemos un -1 en este array de distancia mínima. Con esto sabremos que nodos están ya agregados y cuáles faltan por agregar. El array se inicializa con las distancias de la primera fila de valores del array longitudesAristas. Para el ejemplo de la Figura tenemos [∞, 2, 5, ∞, 6], longitudes del nodo 0 al resto de nodos que se observa en la primera fila de valores del array de longitudes de aristas.
Creamos un array para almacenar el resultado y empezamos el bucle voraz que itera desde 1 hasta n-1, pues estas son las aristas que tenemos que agregar. En cada iteración del bucle se agrega una arista. Vease que el bucle empieza con el índice 1, de tal forma que las posiciones cero de los arrays masProximo y distanciaMinima realmente no se utilizan.
Empezamos el bucle voraz con la iteración i=1. Las distancias mínimas desde el nodo 0 al resto de nodos que tenemos almacenadas son distanciaMinima = [∞, 2, 5, ∞, 6]. Con el primer bucle interno hemos de buscar el nodo k que tenga la menor distancia al nodo anterior 0.
Observando el array de distancias mínimas vemos que es el nodo k=1 cuya distancia 2 es la menor del array. El trozo de código del primer bucle interno que se encarga de buscar el nodo k es el siguiente:
let minimo = Infinity;
let k;
for (let j=1; j<n; j++){
if (distanciaMinima[j]>=0 && distanciaMinima[j]<minimo){
minimo = distanciaMinima[j];
k = j;
}
}Vease que descartamos las distancias -1 de los nodos ya agregados, aunque ahora en esta primera iteración no hay ninguno (sin contar el nodo 0).
let [k] = distanciaMinima.reduce((p,v,j) =>
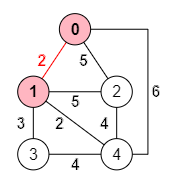
(v>=0 && v<p[1] ? p=[j,v] : null, p), [0, Infinity]);Descubierto el nodo k=1 que está a una menor distancia guardamos el resultado de esta arista, viendo que el array masProximo = [0, 0, 0, 0, 0], siendo por lo tanto el nodo 0 el más próximo puesto que masProximo[1] = 0. Entonces la arista "1,0" se agrega al árbol quedando como muestra la Figura:
resultado.push(`${k},${masProximo[k]}`);Sólo nos queda por hacer en esta iteración la actualización de los dos array: el más próximo y la distancia mínima ahora con respecto al nodo 1 agregado. El trozo de código que se encarga de esto es el siguiente:
distanciaMinima[k] = -1;
for (let j=1; j<n; j++){
if (longitudesAristas[j][k]<distanciaMinima[j]){
distanciaMinima[j] = longitudesAristas[j][k];
masProximo[j] = k;
}
}Le ponemos un valor -1 a la distancia mínima al nodo k=1, con lo que no será tenido en cuenta en la próxima iteración, cuando descubramos el siguiente nodo k. Teniendo en cuenta que teníamos distanciaMinima = [∞, 2, 5, ∞, 6] al anterior nodo 0, iteramos por la columna k=1 del array de longitudesAristas = [2, ∞, 5, 3, 2] (siempre ignorando la primera posición). Comprobamos si la longitud de la arista es menor que la distancia mínima, guardándose este valor en ese caso y actualizando el valor k como nodo más próximo, array que antes estaba como masProximo = [0, 0, 0, 0, 0]. Vease que ∞>2, 5=5, 3<∞ y 2<6 actuándose sólo en los dos últimos nodos. Tras esto nos queda la siguiente situación:
| Nº nodo | Más próximo | Distancia mínima | Notas |
|---|---|---|---|
| 0 | 0 | ∞ | El nodo 0 siempre forma parte del árbol. Se ignoran los valores en los bucles. |
| 1 | 0 | -1 | El nodo 1 forma parte del árbol. Es el que acabamos de agregar. |
| 2 | 0 | 5 | El nodo 2 no forma parte del árbol y está a una distancia 5 del árbol. |
| 3 | 1 | 3 | El nodo 3 no forma parte del árbol y está a una distancia 3. |
| 4 | 1 | 2 | El nodo 4 no forma parte del árbol y está a una distancia 2. Será este nodo k=4 el que agreguemos en la siguiente iteración pues es el que está a menor distancia. |
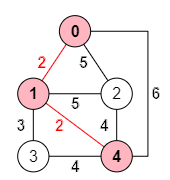
Pasamos a la siguiente iteración i=2. El nodo no agregado que está a menor distancia del árbol es el k=4. Actualizamos arrays quedando:
masProximo = [0, 0, 4, 1, 1] distanciaMinima = [∞, -1, 4, 3, -1] resultado=["1,0","4,1"]
El resultado se observa en la Figura.
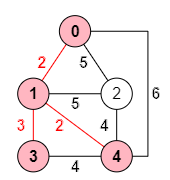
Pasamos a la siguiente iteración i=3. El nodo no agregado que está a menor distancia del árbol es el k=3. Actualizamos arrays quedando:
masProximo=[0,0,4,1,1] distanciaMinima=[∞,-1,4,-1,-1] resultado=["1,0","4,1","3,1"]
El resultado se observa en la Figura.
Pasamos a la siguiente iteración i=4. El nodo no agregado que está a menor distancia del árbol es el k=2. Actualizamos arrays quedando:
masProximo=[0,0,4,1,1] distanciaMinima=[∞,-1,-1,-1,-1] resultado=["1,0","4,1","3,1","2,4"]
El resultado se observa en la Figura. Tenemos ya todos los nodos y aristas en el árbol de recubrimiento mínimo y hemos finalizado.
El coste del algoritmo de Prim
Si prescindimos del coste de construir el array longitudesAristas, el coste del algoritmo de Prim es O(n2). Es obvio deducirlo puesto que el bucle voraz tiene una longitud n-1 al igual que los bucles interiores. Podría pensarse que es peor que el de Kruskal con coste O(a log n), donde a es el número de aristas. Pero si el grafo tiene muchas más aristas que nodos, es preferible el de Prim pues su coste es independiente de las aristas. El máximo de aristas de un grafo con n nodos es n(n-1)/2. En ese caso el coste de Kruskal sería O(n2 log n) superior a O(n2) de Prim.