Árbol recubrimiento mínimo Prim getMinimumSpanningTreePrim()

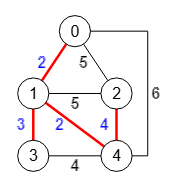
El árbol de recubrimiento mínimo (o MST de Minimum Spanning Tree) en un grafo conexo no dirigido es un subgrafo que conecta todos los nodos y cuyo coste de la suma del valor de las aristas es mínimo.

En el año 2020 expuse unos temas relacionados con los algoritmos voraces. Una aplicación de esos algoritmos se exponía en el tema sobre árboles de recubrimiento mínimo, con el algoritmo de Prim y el algoritmo de Kruskal, algoritmos que ahora adaptamos para integrar en la aplicación de Grafos SVG. En este apartado veremos el algoritmo de Prim.

La aplicación devuelve el siguiente resultado para el grafo de la Figura:

Árbol recubrimiento mínimo (Prim): {
"edges":[[1,0],[4,1],[3,1],[2,4]],
"weight":11,
"trace":[]}

Con este JSON puede importar este ejemplo.

{"nodes":[
    {"index":0,"parent":[{"index":-1}]},
    {"index":1,"parent":[{"index":0,"value":2,"lineTextOffset":-0.8}]},
    {"index":2,"parent":[{"index":0,"value":5,"lineTextOffset":-0.8},{"index":1,"value":5,"lineTextOffset":"0 0.65"}]},
    {"index":3,"parent":[{"index":1,"value":3,"lineTextOffset":-0.8},{"index":4,"value":4,"lineTextOffset":"0 0.65"}]},
    {"index":4,"parent":[{"index":1,"value":2,"lineTextOffset":-1},{"index":2,"value":4,"lineTextOffset":-0.8},{"index":0,"value":6,"lineTextOffset":0.5,"lineOffset":"1"}]}
],
"config":{
    "nodeOffset":"-20",
    "algorithm":"Minimum spanning tree (Prim)"
}}

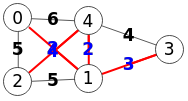
En Wolfram obtenemos el mismo árbol de recubrimiento mínimo con FindSpanningTree[g, Method->"Prim"].

g = WeightedAdjacencyGraph[{{∞,2,5,∞,6},{2,∞,5,3,2},{5,5,∞,∞,4},{∞,3,∞,∞,4},{6,2,4,4,∞}}, ImageSize -> 188, VertexSize -> {"Scaled", 0.17},
VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center], 3 -> Placed[2,Center], 4 -> Placed[3,Center], 5 -> Placed[4,Center]},
VertexLabelStyle -> Directive[Black,17.5], EdgeLabelStyle -> Directive[Black,17.5,Bold], EdgeLabels -> {(2->1)->2, (3->1)->5, (3->2)->5, (4->2)->3, 
(4->5)->4, (5->2)->2, (5->3)->4, (5->1)->6}, VertexStyle -> White, EdgeStyle -> {{Black,Thickness[0.005]}}];
FindSpanningTree[g, Method->"Prim"];
HighlightGraph[g,{Style[EdgeList[%], Red, Thick], Annotation[EdgeList[%], EdgeLabelStyle->Directive[Blue,17.5,Bold]]}]

Las opciones para ejecutar el algoritmo son sólo para su presentación en pantalla con color camino y color texto. Con trazado nos devuelve una traza para ver la ejecución.

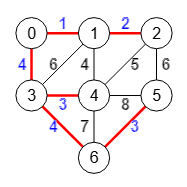
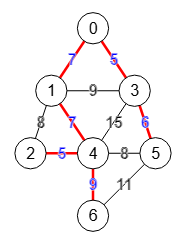
Veamos para el grafo de la Figura su traza para la ejecución de su árbol de recubrimiento mínimo siguiente:

Árbol recubrimiento mínimo (Prim): {
"edges":[[1,0],[2,1],[3,0],
    [4,3],[6,3],[5,6]],
"weight":17,
"trace":[]}

{"nodes":[
    {"index":0,"parent":[{"index":-1}]},
    {"index":3,"parent":[{"index":0,"value":4,"lineTextOffset":-0.6},{"index":1,"value":6,"lineTextOffset":-0.6}]},
    {"index":1,"parent":[{"index":-1},{"index":0,"value":1,"lineTextOffset":"0 -0.6"}]},
    {"index":4,"parent":[{"index":1,"value":4,"lineTextOffset":-0.6},{"index":3,"value":3,"lineTextOffset":"0 0.6"},{"index":2,"value":5,"lineTextOffset":0.6}]},
    {"index":6,"parent":[{"index":4,"value":7,"lineTextOffset":-0.6},{"index":3,"value":4,"lineTextOffset":-0.6},{"index":5,"value":3,"lineTextOffset":0.6}]},
    {"index":2,"parent":[{"index":-1},{"index":1,"value":2,"lineTextOffset":"0 -0.6"}]},
    {"index":5,"parent":[{"index":2,"value":6,"lineTextOffset":0.6},{"index":4,"value":8,"lineTextOffset":"0 0.6"}]}
],
"config":{
    "algorithm":"Minimum spanning tree (Prim)"
}}

Esta es la traza de la ejecución:

INICIO
lengthsEdge = 
[[∞,1,∞,4,∞,∞,∞],
[1,∞,2,6,4,∞,∞],
[∞,2,∞,∞,5,6,∞],
[4,6,∞,∞,3,∞,4],
[∞,4,5,3,∞,8,7],
[∞,∞,6,∞,8,∞,3],
[∞,∞,∞,4,7,3,∞]]

Rellenando arrays siguientes para el nodo 0:
nearest = [0, 0, 0, 0, 0, 0, 0]
minimumDistance = [∞, 1, ∞, 4, ∞, ∞, ∞]

BUCLE VORAZ (a partir del nodo 1):

i=1 k=1 nearest[k]=0 edge="1,0"
    nearest=[0,0,1,0,1,0,0]
    minimumDistance=[∞,-1,2,4,4,∞,∞]
    result=[[1,0]]
i=2 k=2 nearest[k]=1 edge="2,1"
    nearest=[0,0,1,0,1,2,0]
    minimumDistance=[∞,-1,-1,4,4,6,∞]
    result=[[1,0],[2,1]]
i=3 k=3 nearest[k]=0 edge="3,0"
    nearest=[0,0,1,0,3,2,3]
    minimumDistance=[∞,-1,-1,-1,3,6,4]
    result=[[1,0],[2,1],[3,0]]
i=4 k=4 nearest[k]=3 edge="4,3"
    nearest=[0,0,1,0,3,2,3]
    minimumDistance=[∞,-1,-1,-1,-1,6,4]
    result=[[1,0],[2,1],[3,0],[4,3]]
i=5 k=6 nearest[k]=3 edge="6,3"
    nearest=[0,0,1,0,3,6,3]
    minimumDistance=[∞,-1,-1,-1,-1,3,-1]
    result=[[1,0],[2,1],[3,0],[4,3],[6,3]]
i=6 k=5 nearest[k]=6 edge="5,6"
    nearest=[0,0,1,0,3,6,3]
    minimumDistance=[∞,-1,-1,-1,-1,-1,-1]
    result=[[1,0],[2,1],[3,0],[4,3],[6,3],[5,6]]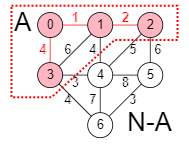

En el tema del año 2020 árboles de recubrimiento mínimo que ya comentamos se explica detalladamente el funcionamiento del algoritmo, repitiendo a continuación parte de esos contenidos. Se basa en un algoritmo voraz, que de forma esquemática, hace lo siguiente:

function voraz(conjunto){
    let resultado = crear(conjunto);
    while (!esSolucion(resultado) && !esVacio(conjunto)){
        let candidato = seleccionar(conjunto);
        if (esCompletable(resultado, candidato)) {
            resultado = guardar(resultado, candidato);
        }
    }
    return resultado;
}

Aplicado al objeto de obtener el árbol de recubrimiento mínimo quedaría así:

function prim(N=[]){
    let resultado = []
    let A = [];
    while (A.length !== N.length){
        let [x, y] = seleccionar(N, A);
        A.push(y);
        resultado.push([x, y]);
    }
    return resultado;
}

En la Figura vemos un momento en la ejecución en la iteración i=4, donde suponemos que el argumento N es un array de nodos que define la estructura del grafo. Es el conjunto del algoritmo voraz sobre el que iteramos. El conjunto A contiene el árbol de recubrimiento mínimo que estamos formando. Para el ejemplo visto antes, en la Figura puede verlo para la iteración i=3. El conjunto N-A contiene los nodos que aún no se han agregado al árbol.

El bucle voraz finalizará cuando A contenga todos los nodos de N. La función para seleccionar un candidato es en este caso también completable. Al seleccionar un nodo, éste debe ya completar la solución. La selección debe obtener una arista formada por la pareja de nodos [x, y] de menor longitud, de tal forma que x ∈ A, y ∈ N-A. Agregamos el nodo y al conjunto A y la arista [x, y] al resultado.

A continuación mostramos el JavaScript del algoritmo getMinimumSpanningTreePrim() que implementa ese voraz, donde prescindimos del código que genera la traza anterior. Se usa isGraphDirected() para saber si el grafo es dirigido, pues no puede aplicarse a grafos dirigidos.

function getMinimumSpanningTreePrim({matrix=[], tracing=false}){
    let result = {edges: [], weight: 0, trace: []}, temp;
    try {
        let n = matrix.length;
        if (temp = isGraphDirected({matrix}), typeof temp==="string") throw new Error(temp);
        if (temp) throw new Error(`The graph is directed and the minimum spanning tree cannot be obtained`);
        let lengthsEdges = matrix.map(v => v.map(w => w===0 ? Infinity : w));
        let nearest = [];
        let minimumDistance = [];
        for (let i=0; i<n; i++){
            nearest[i] = 0;
            minimumDistance[i] = lengthsEdges[i][0];
        }
        for (let i=1; i<n; i++){
            let min = Infinity;
            let k;
            for (let j=1; j<n; j++){
                if (minimumDistance[j]>=0 && minimumDistance[j]<min){
                    min = minimumDistance[j];
                    k = j;
                }
            }
            result.edges.push([k, nearest[k]]);
            result.weight += matrix[k][nearest[k]];
            minimumDistance[k] = -1;
            for (let j=1; j<n; j++){
                if (lengthsEdges[j][k]<minimumDistance[j]){
                    minimumDistance[j] = lengthsEdges[j][k];
                    nearest[j] = k;
                }
            }
        }
    } catch(e) {result = e.message}
    return result;
}

Árbol recubrimiento mínimo Kruskal getMinimumSpanningTreeKruskal()

El algoritmo de Kruskal también es un algoritmo voraz para obtener el árbol de recubrimiento mínimo (o MST de Minimum Spanning Tree), donde ahora la función es completable del esquema básico de un voraz, con el que se comprueba si una arista que se agregue al resultado formará un árbol, se basa en usar la estructura de partición o de conjuntos disjuntos.

La función de selección de nodos para el algoritmo voraz se consigue ordenando las aristas por orden creciente de distancias. Así en cada paso seleccionamos la arista con menor longitud. Si el conjunto de aristas hasta el momento agregadas al resultado no tiene ciclos podrá formarse un árbol, en otro caso se desecha. Y esto se comprueba con la estructura de partición como hemos dicho antes.

Este es el esquema básico de un algoritmo voraz:

function voraz(conjunto){
    let resultado = crear(conjunto);
    while (!esSolucion(resultado) && !esVacio(conjunto)){
        let candidato = seleccionar(conjunto);
        if (esCompletable(resultado, candidato)) {
            resultado = guardar(resultado, candidato);
        }
    }
    return resultado;
}

Recordemos que en el tema Voraces: algoritmo Kruskal explicábamos con detalle este algoritmo, traslandando aquí parte de esos contenidos.

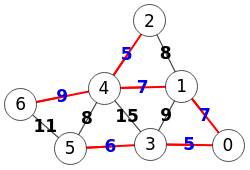
Este es el resultado obtenido en la aplicación para el grafo de la Figura.

Árbol recubrimiento mínimo (Prim): {
"edges":[[0,3],[2,4],[3,5],[0,1],[1,4],[4,6]],
"weight":39,
"trace":[]}

Con este JSON puede importar ese ejemplo.

{"nodes":[
    {"index":0,"parent":[{"index":-1}]},
    {"index":1,"parent":[{"index":0,"value":7}]},
    {"index":2,"parent":[{"index":1,"value":8}]},
    {"index":3,"parent":[{"index":0,"value":5},{"index":1,"value":9}]},
    {"index":4,"parent":[{"index":1,"value":7},{"index":2,"value":5},{"index":3,"value":15}]},
    {"index":5,"parent":[{"index":3,"value":6},{"index":4,"value":8}]},
    {"index":6,"parent":[{"index":4,"value":9},{"index":5,"value":11}]}
],
"config":{
    "algorithm":"Minimum spanning tree (Kruskal)"
}}

En Wolfram obtenemos el mismo árbol de recubrimiento mínimo aplicando la función FindSpanningTree[g, Method->"Kruskal"].

g = WeightedAdjacencyGraph[{{∞,7,∞,5,∞,∞,∞},{7,∞,8,9,7,∞,∞},{∞,8,∞,∞,5,∞,∞},{5,9,∞,∞,15,6,∞},{∞,7,5,15,∞,8,9},{∞,∞,∞,6,8,∞,11},{∞,∞,∞,∞,9,11,∞}}, 
ImageSize -> 250, VertexSize -> {"Scaled", 0.13}, VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center], 3 -> Placed[2,Center], 
4 -> Placed[3,Center], 5 -> Placed[4,Center], 6 -> Placed[5,Center], 7 -> Placed[6,Center]}, VertexLabelStyle -> Directive[Black,17.5], 
EdgeLabelStyle -> Directive[Black,17.5,Bold], EdgeLabels -> {(2->1)->7, (3->2)->8, (4->1)->5, (4->2)->9, (5->2)->7, (5->3)->5, (5->4)->15, (6->4)->6, (6->5)->8, (7->5)->9, (7->6)->11}, 
VertexStyle -> White, EdgeStyle -> {{Black,Thickness[0.005]}}];
FindSpanningTree[g, Method->"Kruskal"];
e = EdgeList[%];
HighlightGraph[g,{Style[e, Red, Thick], Annotation[e, EdgeLabelStyle->Directive[Blue,17.5,Bold]]}]
Total[PropertyValue[{g, e}, EdgeWeight]]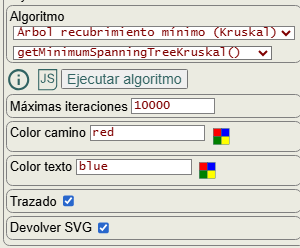

En las opciones para ejecutar el algoritmo de Kruskal vemos en la Figura trazado y devolver SVG. Marcando sólo el trazado nos devuelve los pasos de ejecución en forma de texto. Si además marcamos devolver SVG obtendremos un trozo HTML como el que se expone a continuación. Las opciones color camino y color texto no se pasan al algoritmo pues sólo sirver para dar color a aristas y textos al resultado tras su ejecución.

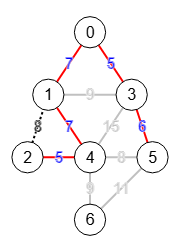
Como ejemplo de ejecución vemos la situación del árbol en el paso i=5 en la traza anterior, donde ya hemos agregado las aristas [[0,3],[2,4],[3,5],[0,1],[1,4]] en el paso anterior y que resaltamos en color rojo en la Figura. Las aristas en color gris no se han tratado y estamos tratando en este paso i=5 la arista [1,2] con línea de puntos en la Figura. Vemos que no podemos agregar esta arista pues se formaría un ciclo en el árbol. Ni tampoco las siguientes [4,5] y [1,3]. Esto se detecta en la estructura de partición al intentar fusionar dos nodos con el mismo rótulo (label).

La siguiente arista [4,6] si es posible pues no forma ciclo, observando que sus rótulos son distintos 2 y 6, como se observa en labels=[0,0,0,0,2,0,6] del paso anterior. Como ya están todos los nodos conectados en un árbol habremos finalizado.

A continuación vemos el JavaScript para ejecutar el algoritmo getMinimumSpanningTreeKruskal(), donde prescindimos del código relacionado con la traza. Usamos isGraphDirected() pues el algoritmo solo aplica a no dirigidos. Y getEdges() para obtener una lista de aristas a partir de la matriz de adyacencia.

function getMinimumSpanningTreeKruskal({matrix=[], tracing=false, returnSvg=false}){
    let result = {edges: [], weight: 0, trace: []}, temp;
    try {
        let n = matrix.length;
        if (temp = isGraphDirected({matrix}), typeof temp==="string") throw new Error(temp);
        if (temp) throw new Error(`The graph is directed and the minimum spanning tree cannot be obtained`);
        let edges = getEdges({matrix, edgesCompact:true, weights:true});
        if (typeof edges==="string") throw new Error(`(1) ${edges}`);
        let edgesOrdered = edges.toSorted((v,w) => v[2]-w[2]).map(v => [v[0], v[1]]);
        let labels = Array.from({length:n}, (v,i) => i);
        let ranges = Array.from({length:n}, () => 0);
        let label1, label2;
        for (let [i, edge] of edgesOrdered.entries()){
            let [index1, index2] = edge;
            let arr = searchLabel({labels, index: index1});
            if (typeof arr==="string") throw new Error(`(2) ${arr}`);
            [label1, labels] = arr;
            arr = searchLabel({labels, index: index2});
            if (typeof arr==="string") throw new Error(`(3) ${arr}`);
            [label2, labels] = arr;
            if (label1 !== label2){
                arr = mergeLabels({labels, ranges, label1, label2});
                if (typeof arr==="string") throw new Error(`(4) ${arr}`);
                [labels, ranges] = arr;
                result.edges.push(edge);
                if (result.edges.length === n-1) break;
            }
        }
        for (let [i, j] of result.edges.values()){
            result.weight += matrix[i][j];
        }
    } catch(e) {result = e.message}
    return result;
}

Recordemos que el algoritmo getEdges({matrix, edgesCompact:true, weights:true} devuelve una lista de aristas con tres posiciones como [i,j,v] siendo "i,j" los nodos de la arista y "v" su valor. Ordenamos por "v" creciente y devolvemos solo los índices de nodos [i, j] en la variable edgesOrdered

La estructura de partición usa estas dos funciones siguientes mergeLabels() para fusionar dos rótulos y searchLabel() para buscar un rótulo:

function mergeLabels({labels=[], ranges=[], label1=0, label2=0}) {
    let result = [];
    try {
        let a = Math.min(label1, label2);
        let b = Math.max(label1, label2);
        if (ranges[a]===ranges[b]){
            labels[b] = a;
            ranges[a]++;
        } else if (ranges[a]>ranges[b]){
            labels[b] = a;
        } else {
            labels[a] = b;
        }
        result = [labels, ranges];
    } catch(e) {result = e.message}
    return result;
}

function searchLabel({labels=[], index=0}) {
    let result = [];
    try {
        let label = index;
        while (labels[label]!==label){
            label = labels[label];
        }
        let i = index;
        while (i!==label){
            [labels[i], i] = [label, labels[i]];
        }
        result = [label, labels];
    } catch(e) {result = e.message}
    return result;
}