Coloreado de grafos
Coloreado grafos Greedy getColoringGreedy()
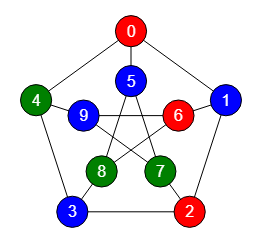
El coloreado de grafos, o más exactamente el coloreado de los nodos de un grafo, consiste en dotar de colores a los nodos de forma que nodos adyacentes no compartan el mismo color. Puede contemplarse también de igual forma el coloreado de aristas tal que que todas las aristas que comparten un nodo tengan colores diferentes, función que expondremos en el apartado con el algoritmo getColoringEdges() al final. En todos los casos para grafos dirigidos se ignoran la direcciones de las aristas coloreándose como si fuera no dirigido.
Los primeros cuatro algoritmos que veremos getColoringGreedy() en este apartado y getColoringWelshPowell(), getColoringBrelaz() y getColoringBacktrack() en siguientes apartados se aplican al coloreado de nodos.
En la Figura vemos el grafo de Petersen donde dos nodos adyacentes no comparten el mismo color, necesitándose como mínimo 3 colores para conseguirlo. El número mínimo de colores para colorear los nodos se denomina número cromático del grafo. Mientras que el índice cromático se reserva para el caso de las aristas.
El grafo anterior se ha coloreado usando el algoritmo voraz getColoringGreedy() con el siguiente resultado, donde vemos que se usan tres colores que se indexan con 1, 2, 3 para rojo, azul y verde respectivamente. Estos índices de colores siempre se inician en 1, reservando el 0 para el caso de sin color. El resultado es un objeto con los campos "colors" que es una lista con tantas posiciones como nodos del grafo, donde cada posición indica el número de color de ese nodo, "partitions" que son las agrupaciones de los nodos en subconjuntos agrupados por número de color y "totalColors" que es el número de colores utilizado, pudiendo coincidir con el número cromático siempre que el algoritmo haya utilizado el menor número de colores posibles, lo cual no se garantiza siempre como veremos después. Si alguna posición es 0 es que el algoritmo no pudo aplicarle color a ese nodo.
Time: 0 ms
Colores: 1→red, 2→blue, 3→green
Coloreado (Greedy): {
"colors":[1,2,1,2,3,2,1,3,3,2],
"partitions":[[0,2,6],[1,3,5,9],[4,7,8]],
"totalColors":3
}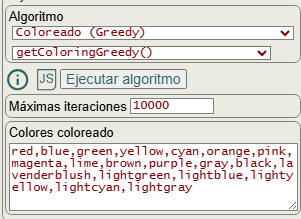
En la Figura vemos la opción colores coloreado con una lista de colores. El algoritmo getColoringGreedy() devuelve una lista de números enteros no negativos que pueden relacionarse con una lista de colores, aunque no necesariamente. Esos números podrían verse como un índice de partición de nodos, por ejemplo. Así que el resultado anterior [1,2,1,2,3,2,1,3,3,2] se corresponde con la partición de nodos siguiente, donde cada partición contiene los nodos del grafo que no están conectados entre sí:
Nodos: 0 1 2 3 4 5 6 7 8 9 Coloreado: [1,2,1,2,3,2,1,3,3,2] Color: 1 2 3 Partición: [[0,2,6],[1,3,5,9],[4,7,8]]
Visualmente se presenta mejor esa partición con colores, con lo que pasamos una lista de colores para ello. Si hay menos colores que los necesarios se vuelve a empezar con la lista de colores de forma rotativa, advirtiéndose de ello en la aplicación, pero en cualquier caso esa lista de colores no se pasa al algoritmo getColoringGreedy(), aplicándose tras devolver el resultado para presentarlo en pantalla.
{"nodes":[
{"index":0,"nodeOffset":"2.5","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"65.54 2.64","parent":[{"index":0}]},
{"index":2,"nodeOffset":"51.01 22.36","parent":[{"index":1}]},
{"index":3,"nodeOffset":"-4.34 -2.64","parent":[{"index":2}]},
{"index":4,"nodeOffset":"-35.54 2.64","parent":[{"index":0},{"index":3}]},
{"index":5,"nodeOffset":"-22.5 -5","parent":[{"index":0}]},
{"index":6,"nodeOffset":"21.52 -16.18","parent":[{"index":1}]},
{"index":7,"nodeOffset":"-2.41 -18.82","parent":[{"index":2},{"index":5}]},
{"index":8,"nodeOffset":"-9.26 -43.82","parent":[{"index":3},{"index":5},{"index":6}]},
{"index":9,"nodeOffset":"-41.52 -16.18","parent":[{"index":4},{"index":6},{"index":7}]}
],
"config":{
"algorithm":"Coloring (Greedy)"
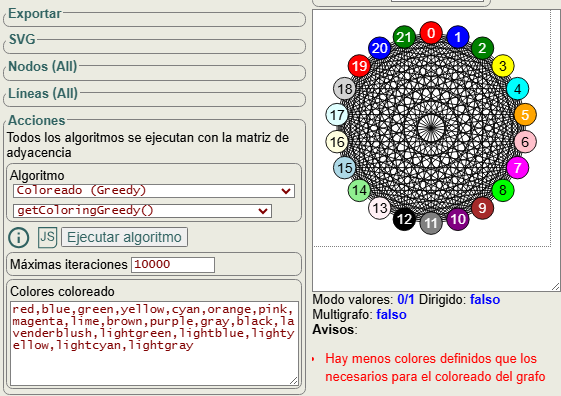
}}En la aplicación se pasa una lista con 19 colores "red, blue, green, yellow,..., lightyellow, lightcyan, lightgray" por defecto, que puede modificarse antes de ejecutar el algoritmo. Como un grafo completo tiene aristas entre todos sus nodos, se necesitan tantos colores como nodos del grafo. Si no se modifica esa lista y coloreamos un grafo completo con más de 19 nodos nos advertirá que hay menos colores definidos que los necesarios para el coloreado del grafo
, como se observa en la Figura siguiente coloreando el grafo completo de 22 nodos, donde a partir del nodo 19 inclusive se vuelven a repetir los colores "red", "blue" y "green".

Agregando los colores "olive", "gold" y "navy" a la opción colores coloreado de la aplicación, se usarán para colorear esos tres últimos nodos 19, 20 y 21 como se observa en la Figura, no emitiendo ningún aviso de error.
Observe que el resultado siguiente que devuelve el algoritmo getColoringGreedy() no incluye nombres de colores, sólo devuelve una lista de números de colores, con el menor número 1. En el resultado no advierte de esa incidencia, pues la aplicación toma posteriormente a la ejecución del algoritmo esa lista de números de colores y les asigna la lista de nombres de colores que se haya pasado en la opción colores coloreado, emitiendo el aviso si no hay nombres de colores suficientes para la lista de números de colores.
Time: 0 ms
Colores: 1→red, 2→blue, 3→green, 4→yellow, 5→cyan, 6→orange, 7→pink, 8→magenta,
9→lime, 10→brown, 11→purple, 12→gray, 13→black, 14→lavenderblush, 15→lightgreen,
16→lightblue, 17→lightyellow, 18→lightcyan, 19→lightgray, 20→olive, 21→gold, 22→navy
Coloreado (Greedy): {
"colors":[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22],
"partitions":[[0],[1],[2],[3],[4],[5],[6],[7],[8],[9],[10],[11],[12],[13],[14],[15],
[16],[17],[18],[19],[20],[21]],
"totalColors":22
}Con este JSON se importa el ejemplo.
{"nodes":[
{"index":0,"nodeOffset":"2.5 -2.35","parent":-1},
{"index":1,"nodeOffset":"59.85 -25.52","parent":0},
{"index":2,"nodeOffset":"66.26 -20.53","parent":[0,1]},
{"index":3,"nodeOffset":"70.78 -12.65","parent":[0,1,2]},
{"index":4,"nodeOffset":"72.75 -2.55","parent":[0,1,2,3]},
{"index":5,"nodeOffset":"71.58 8.99","parent":[0,1,2,3,4]},
{"index":6,"nodeOffset":"67.04 21.02","parent":[0,1,2,3,4,5]},
{"index":7,"nodeOffset":"59.11 32.56","parent":[0,1,2,3,4,5,6]},
{"index":8,"nodeOffset":"48.06 42.67","parent":[0,1,2,3,4,5,6,7]},
{"index":9,"nodeOffset":"34.44 50.54","parent":[0,1,2,3,4,5,6,7,8]},
{"index":10,"nodeOffset":"18.95 55.54","parent":[0,1,2,3,4,5,6,7,8,9]},
{"index":11,"nodeOffset":"2.5 57.24","parent":[0,1,2,3,4,5,6,7,8,9,10]},
{"index":12,"nodeOffset":"-13.95 55.54","parent":[0,1,2,3,4,5,6,7,8,9,10,11]},
{"index":13,"nodeOffset":"-29.44 50.54","parent":[0,1,2,3,4,5,6,7,8,9,10,11,12]},
{"index":14,"nodeOffset":"-43.06 42.67","parent":[0,1,2,3,4,5,6,7,8,9,10,11,12,13]},
{"index":15,"nodeOffset":"-54.11 32.56","parent":[0,1,2,3,4,5,6,7,8,9,10,11,12,13,14]},
{"index":16,"nodeOffset":"-62.04 21.02","parent":[0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]},
{"index":17,"nodeOffset":"-66.58 8.99","parent":[0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]},
{"index":18,"nodeOffset":"-67.75 -2.55","parent":[0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17]},
{"index":19,"nodeOffset":"-65.78 -12.65","parent":[0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18]},
{"index":20,"nodeOffset":"-61.26 -20.53","parent":[0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]},
{"index":21,"nodeOffset":"-54.85 -25.52","parent":[0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]}
],
"config":{
"nodeRadius":5,
"algorithm":"Coloring (Greedy)",
"colorsForColoring":"red,blue,green,yellow,cyan,orange,pink,magenta,lime,brown,purple,gray,black,lavenderblush,lightgreen,lightblue,lightyellow,lightcyan,lightgray,olive,gold,navy"
}}Los algoritmos voraces consideran un conjunto de candidatos que se van analizando, tomando en cada iteración el que a corto plazo resulte más aceptable para conseguir la optimalidad que se espera del resultado final. Una vez seleccionado un candidato se incorpora al resultado, no reconsiderándose más adelante dicha decisión y permaneciendo en la solución hasta el final. Si por alguna razón no llegamos a un resultado óptimo no habrá forma de deshacer las acciones. El JavaScript del algoritmo es muy simple:
function getColoringGreedy({matrix=[]}) {
let result = {colors:[], partitions:[], totalColors:0};
try {
let n = matrix.length;
result.colors = Array.from({length: n}, () => 0);
let colors = Array.from({length: n}, (v,i) => i+1);
for (let i=0; i<n; i++){
let colorsAssigned = [];
for (let j=0; j<n; j++) {
if (iter++, iter>maxIter) return `Maximum iterations '${maxIter}' reached`;
if ((matrix[i][j]!==0 || matrix[j][i]!==0) && result.colors[j]>0){
colorsAssigned.push(result.colors[j]);
}
}
result.colors[i] = colors.filter(v => !colorsAssigned.includes(v))[0];
}
result.totalColors = Math.max(...result.colors);
result.partitions = Array.from({length:result.totalColors}, ()=>[]);
for (let i=0; i<result.colors.length; i++){
result.partitions[result.colors[i]-1].push(i);
}
} catch(e) {result = e.message}
return result;
}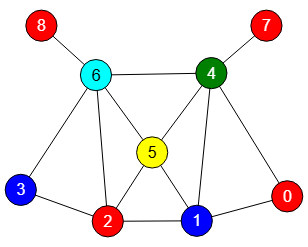
Como hemos dicho, este algoritmo de tipo voraz no siempre consigue el resultado óptimo. Para colorear el grafo de la Figura necesita 5 colores cuando su número cromático es 3, como veremos en el siguiente apartado con otro algoritmo mejor.
Time: 0 ms
Colores: 1→red, 2→blue, 3→green, 4→yellow, 5→cyan
Coloreado (Greedy): {
"colors":[1,2,1,2,3,4,5,1,1],
"partitions":[[0,2,7,8],[1,3],[4],[5],[6]],
"totalColors":5
}
{"nodes":[
{"index":0,"nodeOffset":"65.13 66.2","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"45.54 51","parent":[{"index":0}]},
{"index":2,"nodeOffset":"18.2 26.2","parent":[{"index":1}]},
{"index":3,"nodeOffset":"-25 -11.4","parent":[{"index":2}]},
{"index":4,"nodeOffset":"18.06 -8.2","parent":[{"index":0},{"index":1}]},
{"index":5,"nodeOffset":"11 -1.4","parent":[{"index":1},{"index":2},{"index":4}]},
{"index":6,"nodeOffset":"-28.2 -57.4","parent":[{"index":2},{"index":3},{"index":4},{"index":5}]},
{"index":7,"nodeOffset":"31.8 -52.2","parent":[{"index":4}]},
{"index":8,"nodeOffset":"-33.4 -102.2","parent":[{"index":6}]}
],
"config":{
"algorithm":"Coloring (Greedy)"
}}Coloreado grafos Welsh-Powell getColoringWelshPowell()

Si en el algoritmo voraz que vimos antes iterábamos por los nodos para asignarles un color siguiendo su orden natural 0, 1, 2, ..., con el algoritmo Welsh-Powell antes ordenamos descendente los nodos por su grado que es el número de aristas incidentes en el nodo. Se usa el algoritmo que ya hemos visto getVertexDegrees() que obtiene los grados de todos los nodos. El resto del algoritmo es el mismo que el voraz del apartado anterior.
Ese ordenamiento para el grafo de la Figura es [4,6,1,2,5,0,3,7,8], tratando los nodos de mayor grado primero, lo que permite colorearlo con el mínimo 3 colores.
Time: 1 ms
Colores: 1→red, 2→blue, 3→green
Coloreado (Welsh Powell): {
"colors":[3,2,1,3,1,3,2,2,1],
"partitions":[[2,4,8],[1,6,7],[0,3,5]],
"totalColors":3
}
{"nodes":[
{"index":0,"nodeOffset":"65.13 66.2","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"45.54 51","parent":[{"index":0}]},
{"index":2,"nodeOffset":"18.2 26.2","parent":[{"index":1}]},
{"index":3,"nodeOffset":"-25 -11.4","parent":[{"index":2}]},
{"index":4,"nodeOffset":"18.06 -8.2","parent":[{"index":0},{"index":1}]},
{"index":5,"nodeOffset":"11 -1.4","parent":[{"index":1},{"index":2},{"index":4}]},
{"index":6,"nodeOffset":"-28.2 -57.4","parent":[{"index":2},{"index":3},{"index":4},{"index":5}]},
{"index":7,"nodeOffset":"31.8 -52.2","parent":[{"index":4}]},
{"index":8,"nodeOffset":"-33.4 -102.2","parent":[{"index":6}]}
],
"config":{
"algorithm":"Coloring (Welsh Powell)"
}}A continuación vemos el JavaScript del algoritmo getColoringWelshPowell(), que usa el algoritmo getVertexDegrees() para obtener los grados de los vértices, ordenándose los vértices por ese grado de mayor a menor. El resto del algoritmo es el voraz que vimos en el apartado anterior getColoringGreedy().
function getColoringWelshPowell({matrix=[]}) {
let result = {colors:[], partitions:[], totalColors:0};
try {
let n = matrix.length;
result.colors = Array.from({length: n}, () => 0);
let degrees = getVertexDegrees({matrix});
if (typeof degrees==="string") throw new Error(degrees);
let orderIndexes = degrees.map((v, i) => [i, v]).toSorted((v, w) => w[1]-v[1]).map(v => v[0]);
let colors = Array.from({length: n}, (v,i) => i+1);
for (let index of orderIndexes) {
let colorsAssigned = [];
for (let j=0; j<n; j++) {
if (iter++, iter>maxIter) return `Maximum iterations '${maxIter}' reached`;
if ((matrix[index][j]!==0 || matrix[j][index]!==0) && result.colors[j]>0){
colorsAssigned.push(result.colors[j]);
}
}
result.colors[index] = colors.filter(v => !colorsAssigned.includes(v))[0];
}
result.totalColors = Math.max(...result.colors);
result.partitions = Array.from({length:result.totalColors}, ()=>[]);
for (let i=0; i<result.colors.length; i++){
result.partitions[result.colors[i]-1].push(i);
}
} catch(e) {result = e.message}
return result;
}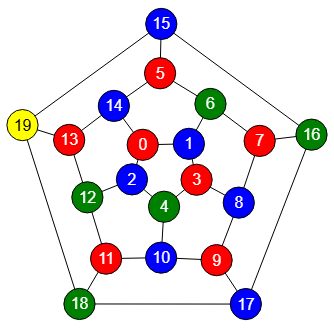
Ordenar los nodos por su grado descendente aún no es suficiente para todos los grafos, pues Welsh-Powell no deja de ser un algoritmo voraz y puede que no encuentre la solución óptima. El grafo de la Figura se colorea con 4 colores con Welsh-Powell cuando su número cromático es 3. Hay que considerar que todos los nodos de este grafo son de grado 3, así que ese orden no aporta ninguna ventaja en estos grafos.
Time: 1 ms
Colores: 1→red, 2→blue, 3→green, 4→yellow
Coloreado (Welsh Powell): {
"colors":[1,2,2,1,3,1,3,1,2,1,2,1,3,1,2,2,3,2,3,4],
"partitions":[[0,3,5,7,9,11,13],[1,2,8,10,14,15,17],[4,6,12,16,18],[19]],
"totalColors":4
}
{"nodes":[
{"index":0,"nodeOffset":"7.11 45.52","parent":[-1,1,14]},
{"index":1,"nodeOffset":"25.58 -54.87","parent":[3,6]},
{"index":2,"nodeOffset":"2.8 34.37","parent":[0,12]},
{"index":3,"nodeOffset":"64.37 -15.47","parent":[4,8]},
{"index":4,"nodeOffset":"15.65 20.33","parent":[2,10]},
{"index":5,"nodeOffset":"54.96 -183.15","parent":[6,15]},
{"index":6,"nodeOffset":"66.03 -170.85","parent":7},
{"index":7,"nodeOffset":"76.63 -156.04","parent":[8,16]},
{"index":8,"nodeOffset":"59.18 -131.31","parent":9},
{"index":9,"nodeOffset":"41.22 -108.26","parent":[10,17]},
{"index":10,"nodeOffset":"9.92 -109.27","parent":11},
{"index":11,"nodeOffset":"-21.19 -108.87","parent":[12,18]},
{"index":12,"nodeOffset":"-37.77 -133.44","parent":13},
{"index":13,"nodeOffset":"-54.14 -156.43","parent":[14,19]},
{"index":14,"nodeOffset":"-45.35 -170.07","parent":5},
{"index":15,"nodeOffset":"35.96 -77.91","parent":16},
{"index":16,"nodeOffset":"81.78 -33.54","parent":17},
{"index":17,"nodeOffset":"41.23 34.33","parent":18},
{"index":18,"nodeOffset":"-39.63 34.29","parent":19},
{"index":19,"nodeOffset":"-76.71 -37.37","parent":15}
],
"config":{
"algorithm":"Coloring (Welsh Powell)"
}}Coloreado grafos Brelaz getColoringBrelaz()
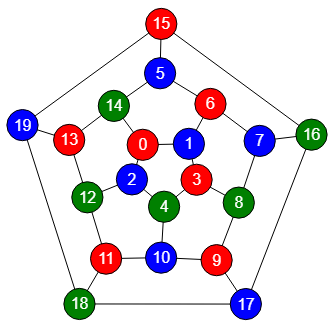
El algoritmo de Brelaz, también denominado DSATUR, es del tipo heurístico que gestiona los nodos en función de su grado de saturación (DSAT) que es el número de colores diferentes de sus nodos vecinos.
Un algoritmo heurístico usa técnicas para encontrar una solución más rápidamente, aunque no siempre se garantiza que se encuentre la solución óptima. Como vemos en la Figura, para este ejemplo encuentra la solución óptima usando el mínimo de 3 colores, cuando Welsh-Powell y Greedy necesitaban 4.
Time: 2 ms
Colores: 1→red, 2→blue, 3→green
Coloreado (Brelaz): {
"colors":[1,2,2,1,3,2,1,2,3,1,2,1,3,1,3,1,3,2,3,2],
"partitions":[[0,3,6,9,11,13,15],[1,2,5,7,10,17,19],[4,8,12,14,16,18]],
"totalColors":3,
"warnings":[]
}
{"nodes":[
{"index":0,"nodeOffset":"7.11 45.52","parent":[-1,1,14]},
{"index":1,"nodeOffset":"25.58 -54.87","parent":[3,6]},
{"index":2,"nodeOffset":"2.8 34.37","parent":[0,12]},
{"index":3,"nodeOffset":"64.37 -15.47","parent":[4,8]},
{"index":4,"nodeOffset":"15.65 20.33","parent":[2,10]},
{"index":5,"nodeOffset":"54.96 -183.15","parent":[6,15]},
{"index":6,"nodeOffset":"66.03 -170.85","parent":7},
{"index":7,"nodeOffset":"76.63 -156.04","parent":[8,16]},
{"index":8,"nodeOffset":"59.18 -131.31","parent":9},
{"index":9,"nodeOffset":"41.22 -108.26","parent":[10,17]},
{"index":10,"nodeOffset":"9.92 -109.27","parent":11},
{"index":11,"nodeOffset":"-21.19 -108.87","parent":[12,18]},
{"index":12,"nodeOffset":"-37.77 -133.44","parent":13},
{"index":13,"nodeOffset":"-54.14 -156.43","parent":[14,19]},
{"index":14,"nodeOffset":"-45.35 -170.07","parent":5},
{"index":15,"nodeOffset":"35.96 -77.91","parent":16},
{"index":16,"nodeOffset":"81.78 -33.54","parent":17},
{"index":17,"nodeOffset":"41.23 34.33","parent":18},
{"index":18,"nodeOffset":"-39.63 34.29","parent":19},
{"index":19,"nodeOffset":"-76.71 -37.37","parent":15}
],
"config":{
"algorithm":"Coloring (Brelaz)"
}}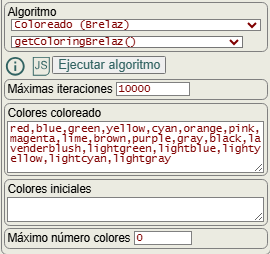
En las opciones para ejecutar el algoritmo que vemos en la Figura, aparte de colores coloreado que ya hemos explicado que son la correpondencia de colores con los números del resultado devuelto, también encontramos máximo número colores que bien puede ser un número entre 1 y el total de nodos del grafo, o bien poner un 0 y el algoritmo buscará el primer número que coloree el grafo, como el ejemplo anterior donde el algoritmo probó con 1 y 2 colores sin poder colorear todos los nodos y, finalmente, si lo consiguió con 3 colores.
En el apartado siguiente veremos como usar la opción colores iniciales.
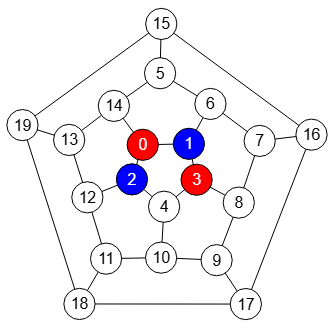
Si en la opción máximo número colores para ese ejemplo imponemos 2 colores, el algoritmo no puede colorear todos los nodos, como se observa en la Figura, que al no tener más colores disponibles no pudo colorear el nodo 4. En este caso se devuelven los colores encontrados y un aviso en el campo "warnings" con el texto The graph cannot be colored with '2' colors
que también se expone junto al grafo en la aplicación.
Time: 0 ms
Colores: 1→red, 2→blue, 3→green
Coloreado (Brelaz): {
"colors":[1,2,2,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
"partitions":[],
"totalColors":0,
"warnings":["The graph cannot be colored with '2' colors"]} 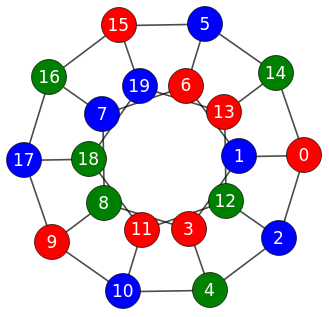
En la Figura vemos como Wolfram colorea el grafo anterior usando VertexColoring[g], función que usa Brelaz como algoritmo de coloreado. Dice ese documento que también podemos pasar el método como VertexColoring[g, Method->"Brelaz"] que se entiende por defecto si no se pasa, permitiendo alternativamente "Optimum" que usa un método de vuelta atrás.
Si quitamos el ";" final de la sentencia c = ResourceFunction["VertexColoring"][g] vemos que se obtienen los colores como una partición con 3 subconjuntos de índices de nodos {{1,4,7,10,12,14,16},{2,3,6,8,11,18,20},{5,9,13,15,17,19}} (recuerde que en Wolfram los índices de nodos se inician en 1 y en nuestra aplicación en 0), tal como explicamos en el primer apartado, así que a cada subconjunto le corresponde el índice de color {1, 2, 3}.
g = AdjacencyGraph[{{0,1,1,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0},{1,0,0,1,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0},
{1,0,0,0,1,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0},{0,1,0,0,1,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0},{0,0,1,1,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0},
{0,0,0,0,0,0,1,0,0,0,0,0,0,0,1,1,0,0,0,0},{0,1,0,0,0,1,0,1,0,0,0,0,0,0,0,0,0,0,0,0},{0,0,0,0,0,0,1,0,1,0,0,0,0,0,0,0,1,0,0,0},
{0,0,0,1,0,0,0,1,0,1,0,0,0,0,0,0,0,0,0,0},{0,0,0,0,0,0,0,0,1,0,1,0,0,0,0,0,0,1,0,0},{0,0,0,0,1,0,0,0,0,1,0,1,0,0,0,0,0,0,0,0},
{0,0,0,0,0,0,0,0,0,0,1,0,1,0,0,0,0,0,1,0},{0,0,1,0,0,0,0,0,0,0,0,1,0,1,0,0,0,0,0,0},{0,0,0,0,0,0,0,0,0,0,0,0,1,0,1,0,0,0,0,1},
{1,0,0,0,0,1,0,0,0,0,0,0,0,1,0,0,0,0,0,0},{0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,1,0,0,1},{0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,1,0,1,0,0},
{0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,1,0,1,0},{0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,1,0,1},{0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,1,0,0,1,0}},
ImageSize -> 329, VertexSize -> {"Scaled", 0.09}, VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center], 3 -> Placed[2,Center],
4 -> Placed[3,Center], 5 -> Placed[4,Center], 6 -> Placed[5,Center], 7 -> Placed[6,Center], 8 -> Placed[7,Center], 9 -> Placed[8,Center],
10 -> Placed[9,Center], 11 -> Placed[10,Center], 12 -> Placed[11,Center], 13 -> Placed[12,Center], 14 -> Placed[13,Center],
15 -> Placed[14,Center], 16 -> Placed[15,Center], 17 -> Placed[16,Center], 18 -> Placed[17,Center], 19 -> Placed[18,Center],
20 -> Placed[19,Center]}, VertexLabelStyle -> Directive[Black,17.5], EdgeLabelStyle -> Directive[Black,17.5,Bold], VertexStyle -> White,
EdgeStyle -> {{Black,Thickness[0.005]}}];
c = ResourceFunction["VertexColoring"][g];
l = Length[c];
t = Take[{Red, Blue, RGBColor["green"], Yellow, Cyan, Orange, Pink, Magenta, Green, Brown, Purple, Gray, Black, RGBColor["lavenderblush"], LightGreen,
LightBlue, LightYellow, LightCyan, LightGray}, l];
m = MapThread[Style, {c, t}];
s = Take[{White, White, White, Black, Black, White, Black, White, Black, White, White, White, White, Black, Black, Black, Black, Black, Black}, l];
n = Length[VertexList[g]];
HighlightGraph[g, m, VertexLabelStyle->Table[i->Directive[s[[Position[c,i][[1,1]]]], 17.5],{i, n}]]

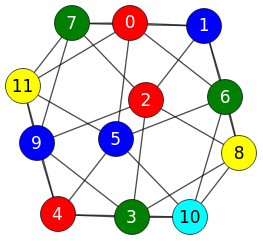
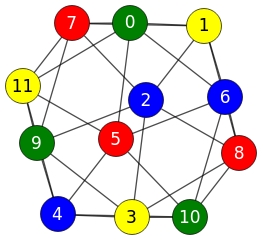
El algoritmo Brelaz no colorea óptimamente algunos grafos como el grafo icosaédrico de la Figura, que puede generar como uno de los grafos Platónicos. Vemos que Brelaz necesita como mínimo 5 colores, pero puede colorearse con 4 colores, como veremos en un apartado más abajo al resolverlo con un vuelta atrás que itera desde 1 color hasta que alcance el menor número de colores para colorear el grafo, pudiéndo entonces afirmar que ese es el número cromático del grafo. Para los algoritmos vistos Greedy, Welsh-Powell o Brelaz (con "0" en la opción máximo número de colores) no se puede afirmar esto.
Time: 0 ms
Colores: 1→red, 2→blue, 3→green, 4→yellow, 5→cyan
Coloreado (Brelaz): {
"colors":[1,2,1,3,1,2,3,3,4,2,5,4],
"partitions":[[0,2,4],[1,5,9],[3,6,7],[8,11],[10]],
"totalColors":5,
"warnings":[]
}
{"nodes":[
{"index":0,"nodeOffset":"2.5 0.17","parent":-1},
{"index":1,"nodeOffset":"70.33 -4.91","parent":0},
{"index":2,"nodeOffset":"53.67 9.91","parent":1},
{"index":3,"nodeOffset":"19.17 4.83","parent":2},
{"index":4,"nodeOffset":"-15.33 -40.09","parent":3},
{"index":5,"nodeOffset":"-15.33 -4.91","parent":[0,4]},
{"index":6,"nodeOffset":"2.5 -4.91","parent":[0,1,5]},
{"index":7,"nodeOffset":"3.08 5.05","parent":[0,1,2]},
{"index":8,"nodeOffset":"3.08 -0.05","parent":[1,2,3,6]},
{"index":9,"nodeOffset":"-14.17 -15.09","parent":[2,3,4,7]},
{"index":10,"nodeOffset":"-31.42 -50.05","parent":[3,4,5,6,8]},
{"index":11,"nodeOffset":"-48.08 5.05","parent":[0,4,5,7,9]}
],
"config":{
"algorithm":"Coloring (Brelaz)",
"maxColors":5
}}
Con Wolfram usando VertexColoring[g] que por defecto usa Method->"Brelaz", también colorea con 5 colores cuando se puede colorear con 4. Se obtiene la partición de nodos {{1,3,5},{2,6,10},{4,7,8},{9,12},{11}} a los que se asignan los colores {1,2,3,4,5}.
g = AdjacencyGraph[{{0,1,0,0,0,1,1,1,0,0,0,1},{1,0,1,0,0,0,1,1,1,0,0,0},{0,1,0,1,0,0,0,1,1,1,0,0},{0,0,1,0,1,0,0,0,1,1,1,0},
{0,0,0,1,0,1,0,0,0,1,1,1},{1,0,0,0,1,0,1,0,0,0,1,1},{1,1,0,0,0,1,0,0,1,0,1,0},{1,1,1,0,0,0,0,0,0,1,0,1},{0,1,1,1,0,0,1,0,0,0,1,0},
{0,0,1,1,1,0,0,1,0,0,0,1},{0,0,0,1,1,1,1,0,1,0,0,0},{1,0,0,0,1,1,0,1,0,1,0,0}}, ImageSize -> 263, VertexSize -> {"Scaled", 0.12},
VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center], 3 -> Placed[2,Center], 4 -> Placed[3,Center], 5 -> Placed[4,Center],
6 -> Placed[5,Center], 7 -> Placed[6,Center], 8 -> Placed[7,Center], 9 -> Placed[8,Center], 10 -> Placed[9,Center], 11 -> Placed[10,Center],
12 -> Placed[11,Center]}, VertexLabelStyle -> Directive[Black,17.5], EdgeLabelStyle -> Directive[Black,17.5,Bold], VertexStyle -> White,
EdgeStyle -> {{Black,Thickness[0.005]}}];
c = ResourceFunction["VertexColoring"][g];
l = Length[c];
t = Take[{Red, Blue, RGBColor["green"], Yellow, Cyan, Orange, Pink, Magenta, Green, Brown, Purple, Gray, Black, RGBColor["lavenderblush"], LightGreen,
LightBlue, LightYellow, LightCyan, LightGray}, l];
m = MapThread[Style, {c, t}];
s = Take[{White, White, White, Black, Black, White, Black, White, Black, White, White, White, White, Black, Black, Black, Black, Black, Black}, l];
n = Length[VertexList[g]];
HighlightGraph[g, m, VertexLabelStyle->Table[i->Directive[s[[Position[c, i][[1, 1]]]], 17.5], {i, n}]]A continuación vemos el JavaScript de este algoritmo getColoringBrelaz() que usa el algoritmo getVertexDegrees() para obtener los grados de los vértices que necesitaremos pasar a la función auxiliar getSaturation() para ordenar los nodos del grafo en ese momento por su grado de saturación que es el número de colores diferentes de sus vecinos ya coloreados. En caso de dos con igual grado de saturación se ordena primero el nodo con mayor grado de aristas incidentes, es decir, el que se obtiene con getVertexDegrees().
function getColoringBrelaz({matrix=[], initialIndexesColoring=[], maxColors=0}) {
let result = {colors:initialIndexesColoring, partitions:[], totalColors:0, warnings:[]};
try {
let n = matrix.length;
if (result.colors.length<n) {
for (let i=result.colors.length; i<n; i++) {
result.colors.push(0);
}
} else if (result.colors.length>n) {
result.colors = result.colors.slice(0, n);
}
let degrees = getVertexDegrees({matrix});
if (typeof degrees==="string") throw new Error(degrees);
let colors = Array.from({length: n}, (v,i) => i+1);
if (maxColors===0) maxColors = n;
while (result.colors.some(v => v===0)) {
if (iter++, iter>maxIter) return `Maximum iterations '${maxIter}' reached`;
let saturation = getSaturation({matrix, nodeColors:result.colors, degrees});
if (typeof saturation==="string") throw new Error(saturation);
let arr = saturation.filter(v => result.colors[v[0]]===0);
if (arr.length===0) throw new Error(`Saturation length is 0`);
let index = arr[0][0];
let colorsAssigned = [];
for (let j=0; j<n; j++) {
if ((matrix[index][j]!==0 || matrix[j][index]!==0) && result.colors[j]>0){
colorsAssigned.push(result.colors[j]);
}
}
let indexColor = colors.filter(v => !colorsAssigned.includes(v))[0];
if (indexColor>maxColors) break;
result.colors[index] = indexColor;
}
if (result.colors.some(v => v===0)) {
if (maxColors>0) {
result.warnings.push(`The graph cannot be colored with '${maxColors}' colors`)
} else {
result.warnings.push(`Could not color graph with '${maxIter}' iterations`)
}
} else {
result.totalColors = Math.max(...result.colors);
result.partitions = Array.from({length:result.totalColors}, ()=>[]);
for (let i=0; i<result.colors.length; i++){
result.partitions[result.colors[i]-1].push(i);
}
}
} catch(e) {result = e.message}
return result;
}Esta es la función auxiliar getSaturation() que usa getParents() para obtener los vecinos de los nodos.
function getSaturation({matrix=[], nodeColors=[], degrees=[]}) {
let result = [];
try {
let n = matrix.length;
result = Array.from({length: n}, (v, i) => [i, 0]);
for (let index=0; index<n; index++) {
let parents = getParents({matrix, index, forceUndirected:true});
if (typeof parents==="string") throw new Error(parents);
result[index] = [index, (new Set(nodeColors.filter((v, i) => v>0 && parents.includes(i)))).size];
}
result = result.toSorted((v, w) => {
if (v[1]===w[1]){
return degrees[w[0]]-degrees[v[0]];
} else {
return w[1]-v[1];
}
});
} catch(e) {result = e.message}
return result;
}Usando algoritmo Brelaz para resolver un Sudoku

En un tema anterior vimos como generar y colorear un grafo Sudoku. El mismo contenido de ese apartado lo trasladamos aquí, pues se usa el algoritmo Brelaz para ese cometido. En las opciones del algoritmo que vemos en la Figura están colores iniciales y máximo número colores que vamos a usar ahora.
5 3 0 0 7 0 0 0 0 6 0 0 1 9 5 0 0 0 0 9 8 0 0 0 0 6 0 8 0 0 0 6 0 0 0 3 4 0 0 8 0 3 0 0 1 7 0 0 0 2 0 0 0 6 0 6 0 0 0 0 2 8 0 0 0 0 4 1 9 0 0 5 0 0 0 0 8 0 0 7 9
Como se observa en la Figura, podemos pasar una lista de colores iniciales de tantos números enteros en el rango 0-9 como nodos tenga el grafo, 81 en el caso del grafo Sudoku. Se define una lista de colores coloreado red, blue, green, ... que se hace corresponder con los números 1, 2, 3, ..., de tal forma que si ponemos un 0 en la lista de colores iniciales significará que ese nodo está sin colorear. Para un grafo Sudoku esta lista de colores iniciales viene a ser el Sudoku parcialmente lleno que encontramos en este juego, que podemos denominar tablero inicial.
El campo máximo número de colores puede ser un valor 0 significando que no hay límite para el máximo o en otro caso se utilizará ese valor como límite. Para un grafo Sudoku podemos poner que el máximo número de colores a utilizar serán 9.
Puede usar el siguiente JSON para importar el grafo Sudoku con esas opciones en la aplicación. O bien generar un Sudoku vacío en el panel asistente generación accediendo con el el botón
{"nodes":[
{"index":0,"nodeOffset":"-31.25 6.25","parent":-1},
{"index":1,"nodeOffset":"32.74 -18.75","parent":0},
{"index":2,"nodeOffset":"46.73 -18.75","parent":[0,1]},
{"index":3,"nodeOffset":"60.71 -18.75","parent":[0,1,2]},
{"index":4,"nodeOffset":"74.7 -18.75","parent":[0,1,2,3]},
{"index":5,"nodeOffset":"88.69 -18.75","parent":[0,1,2,3,4]},
{"index":6,"nodeOffset":"102.68 -18.75","parent":[0,1,2,3,4,5]},
{"index":7,"nodeOffset":"116.67 -18.75","parent":[0,1,2,3,4,5,6]},
{"index":8,"nodeOffset":"130.65 -18.75","parent":[0,1,2,3,4,5,6,7]},
{"index":9,"nodeOffset":"-24.11","parent":[0,1,2]},
{"index":10,"nodeOffset":"-10.12","parent":[0,1,2,9]},
{"index":11,"nodeOffset":"3.87","parent":[0,1,2,9,10]},
{"index":12,"nodeOffset":"73.36 -25","parent":[3,4,5,9,10,11]},
{"index":13,"nodeOffset":"90.47 -25","parent":[3,4,5,9,10,11,12]},
{"index":14,"nodeOffset":"107.58 -25","parent":[3,4,5,9,10,11,12,13]},
{"index":15,"nodeOffset":"124.69 -25","parent":[6,7,8,9,10,11,12,13,14]},
{"index":16,"nodeOffset":"141.8 -25","parent":[6,7,8,9,10,11,12,13,14,15]},
{"index":17,"nodeOffset":"158.91 -25","parent":[6,7,8,9,10,11,12,13,14,15,16]},
{"index":18,"nodeOffset":"-38.39 18.75","parent":[0,1,2,9,10,11]},
{"index":19,"nodeOffset":"-24.4 18.75","parent":[0,1,2,9,10,11,18]},
{"index":20,"nodeOffset":"-10.42 18.75","parent":[0,1,2,9,10,11,18,19]},
{"index":21,"nodeOffset":"63.52 -6.25","parent":[3,4,5,12,13,14,18,19,20]},
{"index":22,"nodeOffset":"80.64 -6.25","parent":[3,4,5,12,13,14,18,19,20,21]},
{"index":23,"nodeOffset":"97.75 -6.25","parent":[3,4,5,12,13,14,18,19,20,21,22]},
{"index":24,"nodeOffset":"114.86 -6.25","parent":[6,7,8,15,16,17,18,19,20,21,22,23]},
{"index":25,"nodeOffset":"131.97 -6.25","parent":[6,7,8,15,16,17,18,19,20,21,22,23,24]},
{"index":26,"nodeOffset":"149.08 -6.25","parent":[6,7,8,15,16,17,18,19,20,21,22,23,24,25]},
{"index":27,"nodeOffset":"-52.68 37.5","parent":[0,9,18]},
{"index":28,"nodeOffset":"16.19 12.5","parent":[1,10,19,27]},
{"index":29,"nodeOffset":"33.3 12.5","parent":[2,11,20,27,28]},
{"index":30,"nodeOffset":"50.41 12.5","parent":[3,12,21,27,28,29]},
{"index":31,"nodeOffset":"67.52 12.5","parent":[4,13,22,27,28,29,30]},
{"index":32,"nodeOffset":"84.63 12.5","parent":[5,14,23,27,28,29,30,31]},
{"index":33,"nodeOffset":"101.74 12.5","parent":[6,15,24,27,28,29,30,31,32]},
{"index":34,"nodeOffset":"118.85 12.5","parent":[7,16,25,27,28,29,30,31,32,33]},
{"index":35,"nodeOffset":"135.96 12.5","parent":[8,17,26,27,28,29,30,31,32,33,34]},
{"index":36,"nodeOffset":"-57.44 56.25","parent":[0,9,18,27,28,29]},
{"index":37,"nodeOffset":"3.07 31.25","parent":[1,10,19,27,28,29,36]},
{"index":38,"nodeOffset":"20.18 31.25","parent":[2,11,20,27,28,29,36,37]},
{"index":39,"nodeOffset":"37.3 31.25","parent":[3,12,21,30,31,32,36,37,38]},
{"index":40,"nodeOffset":"54.41 31.25","parent":[4,13,22,30,31,32,36,37,38,39]},
{"index":41,"nodeOffset":"71.52 31.25","parent":[5,14,23,30,31,32,36,37,38,39,40]},
{"index":42,"nodeOffset":"88.63 31.25","parent":[6,15,24,33,34,35,36,37,38,39,40,41]},
{"index":43,"nodeOffset":"105.74 31.25","parent":[7,16,25,33,34,35,36,37,38,39,40,41,42]},
{"index":44,"nodeOffset":"122.85 31.25","parent":[8,17,26,33,34,35,36,37,38,39,40,41,42,43]},
{"index":45,"nodeOffset":"-62.2 75","parent":[0,9,18,27,28,29,36,37,38]},
{"index":46,"nodeOffset":"-10.04 50","parent":[1,10,19,27,28,29,36,37,38,45]},
{"index":47,"nodeOffset":"7.07 50","parent":[2,11,20,27,28,29,36,37,38,45,46]},
{"index":48,"nodeOffset":"24.18 50","parent":[3,12,21,30,31,32,39,40,41,45,46,47]},
{"index":49,"nodeOffset":"41.29 50","parent":[4,13,22,30,31,32,39,40,41,45,46,47,48]},
{"index":50,"nodeOffset":"58.4 50","parent":[5,14,23,30,31,32,39,40,41,45,46,47,48,49]},
{"index":51,"nodeOffset":"75.51 50","parent":[6,15,24,33,34,35,42,43,44,45,46,47,48,49,50]},
{"index":52,"nodeOffset":"92.62 50","parent":[7,16,25,33,34,35,42,43,44,45,46,47,48,49,50,51]},
{"index":53,"nodeOffset":"109.73 50","parent":[8,17,26,33,34,35,42,43,44,45,46,47,48,49,50,51,52]},
{"index":54,"nodeOffset":"-66.96 93.75","parent":[0,9,18,27,36,45]},
{"index":55,"nodeOffset":"-23.16 68.75","parent":[1,10,19,28,37,46,54]},
{"index":56,"nodeOffset":"-6.05 68.75","parent":[2,11,20,29,38,47,54,55]},
{"index":57,"nodeOffset":"11.07 68.75","parent":[3,12,21,30,39,48,54,55,56]},
{"index":58,"nodeOffset":"28.18 68.75","parent":[4,13,22,31,40,49,54,55,56,57]},
{"index":59,"nodeOffset":"45.29 68.75","parent":[5,14,23,32,41,50,54,55,56,57,58]},
{"index":60,"nodeOffset":"62.4 68.75","parent":[6,15,24,33,42,51,54,55,56,57,58,59]},
{"index":61,"nodeOffset":"79.51 68.75","parent":[7,16,25,34,43,52,54,55,56,57,58,59,60]},
{"index":62,"nodeOffset":"96.62 68.75","parent":[8,17,26,35,44,53,54,55,56,57,58,59,60,61]},
{"index":63,"nodeOffset":"-71.73 112.5","parent":[0,9,18,27,36,45,54,55,56]},
{"index":64,"nodeOffset":"-36.27 87.5","parent":[1,10,19,28,37,46,54,55,56,63]},
{"index":65,"nodeOffset":"-19.16 87.5","parent":[2,11,20,29,38,47,54,55,56,63,64]},
{"index":66,"nodeOffset":"-2.05 87.5","parent":[3,12,21,30,39,48,57,58,59,63,64,65]},
{"index":67,"nodeOffset":"15.06 87.5","parent":[4,13,22,31,40,49,57,58,59,63,64,65,66]},
{"index":68,"nodeOffset":"32.17 87.5","parent":[5,14,23,32,41,50,57,58,59,63,64,65,66,67]},
{"index":69,"nodeOffset":"49.28 87.5","parent":[6,15,24,33,42,51,60,61,62,63,64,65,66,67,68]},
{"index":70,"nodeOffset":"66.39 87.5","parent":[7,16,25,34,43,52,60,61,62,63,64,65,66,67,68,69]},
{"index":71,"nodeOffset":"83.5 87.5","parent":[8,17,26,35,44,53,60,61,62,63,64,65,66,67,68,69,70]},
{"index":72,"nodeOffset":"-76.49 131.25","parent":[0,9,18,27,36,45,54,55,56,63,64,65]},
{"index":73,"nodeOffset":"-49.39 106.25","parent":[1,10,19,28,37,46,54,55,56,63,64,65,72]},
{"index":74,"nodeOffset":"-32.27 106.25","parent":[2,11,20,29,38,47,54,55,56,63,64,65,72,73]},
{"index":75,"nodeOffset":"-15.16 106.25","parent":[3,12,21,30,39,48,57,58,59,66,67,68,72,73,74]},
{"index":76,"nodeOffset":"1.95 106.25","parent":[4,13,22,31,40,49,57,58,59,66,67,68,72,73,74,75]},
{"index":77,"nodeOffset":"19.06 106.25","parent":[5,14,23,32,41,50,57,58,59,66,67,68,72,73,74,75,76]},
{"index":78,"nodeOffset":"36.17 106.25","parent":[6,15,24,33,42,51,60,61,62,69,70,71,72,73,74,75,76,77]},
{"index":79,"nodeOffset":"53.28 106.25","parent":[7,16,25,34,43,52,60,61,62,69,70,71,72,73,74,75,76,77,78]},
{"index":80,"nodeOffset":"70.39 106.25","parent":[8,17,26,35,44,53,60,61,62,69,70,71,72,73,74,75,76,77,78,79]}
],
"config":{
"algorithm":"Coloring (Brelaz)",
"initialIndexesColoring":"5 3 0 0 7 0 0 0 0\n6 0 0 1 9 5 0 0 0\n0 9 8 0 0 0 0 6 0\n8 0 0 0 6 0 0 0 3\n4 0 0 8 0 3 0 0 1\n7 0 0 0 2 0 0 0 6\n0 6 0 0 0 0 2 8 0\n0 0 0 4 1 9 0 0 5\n0 0 0 0 8 0 0 7 9",
"maxColors":9
}}
En la Figura vemos como el algoritmo Brelaz colorea el grafo Sudoku usando solo 9 colores. Y esto es lo mismo que resolver el juego, pues cada color red, blue, green, yellow, ... indica un número de color {1, 2, 3, ..., 9} que son los números que van en cada casilla del tablero. Vemos que cada fila, columna y caja contiene un color distinto para cada uno de sus 9 nodos.
La aplicación devuelve también el siguiente resultado, donde observamos la asociación de números de colores 1→red, 2→blue, 3→green, 4→yellow, 5→cyan, 6→orange, 7→pink, 8→magenta, 9→lime y el tablero Sudoku finalizado, indicando que se han usado Número de colores = 9.
Time: 15 ms
Colores: 1→red, 2→blue, 3→green, 4→yellow, 5→cyan, 6→orange, 7→pink, 8→magenta, 9→lime
Coloreado (Brelaz): {
"colors":[
5,3,4,6,7,8,9,1,2,
6,7,2,1,9,5,3,4,8,
1,9,8,3,4,2,5,6,7,
8,5,9,7,6,1,4,2,3,
4,2,6,8,5,3,7,9,1,
7,1,3,9,2,4,8,5,6,
9,6,1,5,3,7,2,8,4,
2,8,7,4,1,9,6,3,5,
3,4,5,2,8,6,1,7,9
],
"partitions":[
[7,12,18,32,44,46,56,67,78],
[8,11,23,34,37,49,60,63,75],
[1,15,21,35,41,47,58,70,72],
[2,16,22,33,36,50,62,66,73],
[0,14,24,28,40,52,57,71,74],
[3,9,25,31,38,53,55,69,77],
[4,10,26,30,42,45,59,65,79],
[5,17,20,27,39,51,61,64,76],
[6,13,19,29,43,48,54,68,80]
],
"totalColors":9,
"warnings":[]
}
Hice la aplicación SUDOKU hace ya tiempo para resolver este juego usando una serie de técnicas y, como último recurso, mediante un algoritmo del tipo vuelta atrás. En la Figura puede ver como resolvemos el tablero inicial que antes resolvimos usando el coloreado Brelaz.
5,3,4,6,7,8,9,1,2, 6,7,2,1,9,5,3,4,8, 1,9,8,3,4,2,5,6,7, 8,5,9,7,6,1,4,2,3, 4,2,6,8,5,3,7,9,1, 7,1,3,9,2,4,8,5,6, 9,6,1,5,3,7,2,8,4, 2,8,7,4,1,9,6,3,5, 3,4,5,2,8,6,1,7,9
Obtenemos exactamente la misma solución usando otras técnicas en la aplicación Sudoku, pero por ahora no he implementado el coloreado en esa aplicación, pues como veremos a continuación, el coloreado Brelaz no resuelve todos los Sudokus.

El coloreado Brelaz sólo resuelve los Sudokus más simples como hemos dicho. En la Figura vemos como el algoritmo no puede resolver el Sudoku siguiente con 26 números iniciales:
2 0 6 3 0 0 8 9 0 0 0 0 0 1 0 6 0 0 0 3 9 0 0 0 0 0 0 3 0 0 6 2 0 1 0 0 1 0 0 0 4 0 0 5 0 0 8 0 0 0 0 0 3 0 0 4 0 0 0 6 0 0 0 6 0 0 5 0 0 0 0 8 8 0 0 0 0 1 0 0 9
2,1,6,3,5,4,8,9,7, 4,5,8,7,1,9,6,2,3, 7,3,9,2,6,8,4,1,5, 3,7,5,6,2,0,1,8,4, 1,0,0,0,4,0,0,5,0, 0,8,0,0,0,0,0,3,0, 0,4,0,0,0,6,0,7,0, 6,0,0,5,0,0,0,4,8, 8,0,0,4,0,1,0,6,9
Cuando sobrepasa los 9 colores máximos que hemos impuesto finalizará la ejecución devolviendo los 10 primeros colores 1→red, 2→blue, 3→green, 4→yellow, 5→cyan, 6→orange, 7→pink, 8→magenta, 9→lime, 10→brown y dejando muchos nodos sin color, con valor 0 en el array de salida. Si no imponemos máximo número de colores o bien imponemos 10 colores, veremos que precisamente necesitará 10 colores para colorearlo, por lo que no será una solución de un Sudoku 9×9.

Se resuelve en la aplicación Sudoku con la solución de la Figura sin usar vuelta atrás.
2 1 6 3 5 7 8 9 4 7 5 8 9 1 4 6 2 3 4 3 9 2 6 8 5 7 1 3 9 4 6 2 5 1 8 7 1 6 7 8 4 3 9 5 2 5 8 2 1 7 9 4 3 6 9 4 3 7 8 6 2 1 5 6 7 1 5 9 2 3 4 8 8 2 5 4 3 1 7 6 9
Un algoritmo vuelta atrás (backtracking) es del tipo "fuerza bruta" que, en caso de tener solución, siempre se encuentra aunque conlleve el tiempo necesario para recorrer todas las posibles alternativas, siendo por tanto la técnica menos eficiente que se aplica en Sudoku cuando ninguna otra ha conseguido resolverlo.
Naked single: 34 Hidden single: 21 Hidden pair: 1 Locked: 3 W-wing: 1 Hidden rectangle (I): 2 Finned X-wing: 1 Finned Swordfish: 3 Finned Jellyfish: 1 Finned Franken Swordfish (base): 1 Sashimi Franken Swordfish (base): 1
La aplicación Sudoku encuentra los 55 números restantes con estas técnicas que podemos encuadrarlas dentro del tipo heurísticas.
En el siguiente apartado veremos que podemos resolverlo con el algoritmo getColoringBacktrack() en esta aplicación de Grafos, usando un vuelta atrás con lo que siempre encuentra el resultado en caso de que exista.
Coloreado grafos con vuelta atrás getColoringBacktrack()
El algoritmo vuelta atrás siempre devuelve la solución óptima en caso de que exista, lo que supone sacrificar rápidez por precisión, pues se trata de un método de fuerza bruta que inspecciona todas las alternativas hasta que llega a la solución óptima. En el tema recursivos en algoritmos del tipo vuelta atrás ya hablamos de estos algoritmos exponiendo varios problemas que se solucionaban con el vuelta atrás.
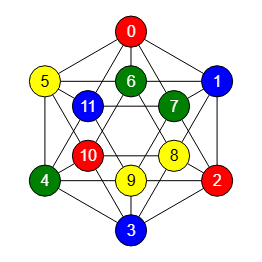
En la Figura vemos el grafo icosaédrico coloreado con el mínimo de 4 colores usando el vuelta atrás, grafo que puede generar como uno de los grafos Platónicos.
Time: 0 ms
Colores: 1→red, 2→blue, 3→green, 4→yellow
Coloring (Backtrack): {
"colors":[1,2,1,2,3,4,3,3,4,4,1,2],
"partitions":[[0,2,10],[1,3,11],[4,6,7],[5,8,9]],
"totalColors":4
}
{"nodes":[
{"index":0,"nodeOffset":"2.5 0.17","parent":-1},
{"index":1,"nodeOffset":"70.33 -4.91","parent":0},
{"index":2,"nodeOffset":"53.67 9.91","parent":1},
{"index":3,"nodeOffset":"19.17 4.83","parent":2},
{"index":4,"nodeOffset":"-15.33 -40.09","parent":3},
{"index":5,"nodeOffset":"-15.33 -4.91","parent":[0,4]},
{"index":6,"nodeOffset":"2.5 -4.91","parent":[0,1,5]},
{"index":7,"nodeOffset":"3.08 5.05","parent":[0,1,2]},
{"index":8,"nodeOffset":"3.08 -0.05","parent":[1,2,3,6]},
{"index":9,"nodeOffset":"-14.17 -15.09","parent":[2,3,4,7]},
{"index":10,"nodeOffset":"-31.42 -50.05","parent":[3,4,5,6,8]},
{"index":11,"nodeOffset":"-48.08 5.05","parent":[0,4,5,7,9]}
],
"config":{
"algorithm":"Coloring (Backtrack)",
"maxColors":4
}}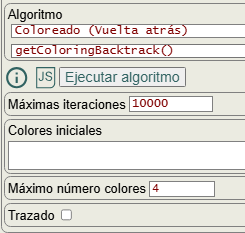
En la Figura vemos las opciones para ejecutar getColoringBacktrack(). La opción máximo número colores es un número entre 1 y el total de nodos del grafo. Para colorear este grafo hemos de poner 4 o más pues con menos no se puede colorear ese grafo. O bien poner un 0 y el algoritmo buscará ese mínimo número de colores también denominado número cromático.
La opción colores iniciales se expone más abajo con el ejemplo del coloreado Sudoku. La opción trazado se verá cuando expongamos el código del algoritmo.
En Wolfram con FindVertexColoring[g, k] encuentra el coloreado con menor número de colores, aunque no explica que método usa. El argumento "k" es una lista de colores, si no se pasa devuelve la lista de índices de colores {3,4,2,4,2,1,2,1,1,3,3,4} con números entre 1 y 4.
g = AdjacencyGraph[{{0,1,0,0,0,1,1,1,0,0,0,1},{1,0,1,0,0,0,1,1,1,0,0,0},{0,1,0,1,0,0,0,1,1,1,0,0},{0,0,1,0,1,0,0,0,1,1,1,0},
{0,0,0,1,0,1,0,0,0,1,1,1},{1,0,0,0,1,0,1,0,0,0,1,1},{1,1,0,0,0,1,0,0,1,0,1,0},{1,1,1,0,0,0,0,0,0,1,0,1},{0,1,1,1,0,0,1,0,0,0,1,0},
{0,0,1,1,1,0,0,1,0,0,0,1},{0,0,0,1,1,1,1,0,1,0,0,0},{1,0,0,0,1,1,0,1,0,1,0,0}}, ImageSize -> 263, VertexSize -> {"Scaled", 0.12},
VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center], 3 -> Placed[2,Center], 4 -> Placed[3,Center], 5 -> Placed[4,Center],
6 -> Placed[5,Center], 7 -> Placed[6,Center], 8 -> Placed[7,Center], 9 -> Placed[8,Center], 10 -> Placed[9,Center], 11 -> Placed[10,Center],
12 -> Placed[11,Center]}, VertexLabelStyle -> Directive[Black,17.5], EdgeLabelStyle -> Directive[Black,17.5,Bold], VertexStyle -> White, EdgeStyle -> {{Black,Thickness[0.005]}}];
k = {Red, Blue, RGBColor["green"], Yellow, Cyan, Orange, Pink, Magenta, Green, Brown, Purple, Gray, Black, RGBColor["lavenderblush"], LightGreen, LightBlue, LightYellow, LightCyan, LightGray};
c = FindVertexColoring[g, k];
d = Flatten[Table[Position[k,i], {i,c}]];
t = Take[{White, White, White, Black, Black, White, Black, White, Black, White, White, White, White, Black, Black, Black, Black, Black, Black}, Length[d]];
s = Table[Directive[t[[i]], 17.5], {i, d}];
v = VertexList[g];
Annotate[g, {VertexStyle->Thread[v->c],VertexLabelStyle->Thread[v->s]}]Las líneas con las variables d, t, s podrían eliminarse y sustituir la última línea por Annotate[g, {VertexStyle -> Thread[v->c]}] afectando sólo al color contrastado del texto de los nodos, como por ejemplo, con fondo rojo, azul o verde se pone texto de color blanco y con fondo amarillo más claro se pone texto de color negro.

En la Figura vimos que Brelaz no podía resolver el Sudoku de la Figura que ahora el vuelta atrás si resuelve.
2 0 6 3 0 0 8 9 0 0 0 0 0 1 0 6 0 0 0 3 9 0 0 0 0 0 0 3 0 0 6 2 0 1 0 0 1 0 0 0 4 0 0 5 0 0 8 0 0 0 0 0 3 0 0 4 0 0 0 6 0 0 0 6 0 0 5 0 0 0 0 8 8 0 0 0 0 1 0 0 9
Estos son los 26 números iniciales del Sudoku que pasaremos en la opción colores iniciales que vimos en la Figura.
Time: 6 ms
Colores: 1→red, 2→blue, 3→green, 4→yellow, 5→cyan, 6→orange, 7→pink, 8→magenta, 9→lime
Coloring (Backtrack): {
"colors":[
2,1,6,3,5,7,8,9,4,
7,5,8,9,1,4,6,2,3,
4,3,9,2,6,8,5,7,1,
3,9,4,6,2,5,1,8,7,
1,6,7,8,4,3,9,5,2,
5,8,2,1,7,9,4,3,6,
9,4,3,7,8,6,2,1,5,
6,7,1,5,9,2,3,4,8,
8,2,5,4,3,1,7,6,9
],
"partitions":[
[1,13,26,33,36,48,61,65,77],
[0,16,21,31,44,47,60,68,73],
[3,17,19,27,41,52,56,69,76],
[8,14,18,29,40,51,55,70,75],
[4,10,24,32,43,45,62,66,74],
[2,15,22,30,37,53,59,63,79],
[5,9,25,35,38,49,57,64,78],
[6,11,23,34,39,46,58,71,72],
[7,12,20,28,42,50,54,67,80]
],
"totalColors":9
}
{"nodes":[
{"index":0,"nodeOffset":"-39.21 -1.71","parent":-1},
{"index":1,"nodeOffset":"20.52 -26.71","parent":0},
{"index":2,"nodeOffset":"30.25 -26.71","parent":[0,1]},
{"index":3,"nodeOffset":"39.97 -26.71","parent":[0,1,2]},
{"index":4,"nodeOffset":"49.7 -26.71","parent":[0,1,2,3]},
{"index":5,"nodeOffset":"59.43 -26.71","parent":[0,1,2,3,4]},
{"index":6,"nodeOffset":"69.16 -26.71","parent":[0,1,2,3,4,5]},
{"index":7,"nodeOffset":"78.89 -26.71","parent":[0,1,2,3,4,5,6]},
{"index":8,"nodeOffset":"88.61 -26.71","parent":[0,1,2,3,4,5,6,7]},
{"index":9,"nodeOffset":"-32.07 -12.22","parent":[0,1,2]},
{"index":10,"nodeOffset":"-22.34 -12.22","parent":[0,1,2,9]},
{"index":11,"nodeOffset":"-12.61 -12.22","parent":[0,1,2,9,10]},
{"index":12,"nodeOffset":"52.62 -37.22","parent":[3,4,5,9,10,11]},
{"index":13,"nodeOffset":"65.47 -37.22","parent":[3,4,5,9,10,11,12]},
{"index":14,"nodeOffset":"78.32 -37.22","parent":[3,4,5,9,10,11,12,13]},
{"index":15,"nodeOffset":"91.17 -37.22","parent":[6,7,8,9,10,11,12,13,14]},
{"index":16,"nodeOffset":"104.02 -37.22","parent":[6,7,8,9,10,11,12,13,14,15]},
{"index":17,"nodeOffset":"116.87 -37.22","parent":[6,7,8,9,10,11,12,13,14,15,16]},
{"index":18,"nodeOffset":"-46.35 2.27","parent":[0,1,2,9,10,11]},
{"index":19,"nodeOffset":"-36.62 2.27","parent":[0,1,2,9,10,11,18]},
{"index":20,"nodeOffset":"-26.9 2.27","parent":[0,1,2,9,10,11,18,19]},
{"index":21,"nodeOffset":"42.78 -22.73","parent":[3,4,5,12,13,14,18,19,20]},
{"index":22,"nodeOffset":"55.64 -22.73","parent":[3,4,5,12,13,14,18,19,20,21]},
{"index":23,"nodeOffset":"68.49 -22.73","parent":[3,4,5,12,13,14,18,19,20,21,22]},
{"index":24,"nodeOffset":"81.34 -22.73","parent":[6,7,8,15,16,17,18,19,20,21,22,23]},
{"index":25,"nodeOffset":"94.19 -22.73","parent":[6,7,8,15,16,17,18,19,20,21,22,23,24]},
{"index":26,"nodeOffset":"107.04 -22.73","parent":[6,7,8,15,16,17,18,19,20,21,22,23,24,25]},
{"index":27,"nodeOffset":"-60.64 16.76","parent":[0,9,18]},
{"index":28,"nodeOffset":"3.97 -8.24","parent":[1,10,19,27]},
{"index":29,"nodeOffset":"16.82 -8.24","parent":[2,11,20,27,28]},
{"index":30,"nodeOffset":"29.67 -8.24","parent":[3,12,21,27,28,29]},
{"index":31,"nodeOffset":"42.52 -8.24","parent":[4,13,22,27,28,29,30]},
{"index":32,"nodeOffset":"55.37 -8.24","parent":[5,14,23,27,28,29,30,31]},
{"index":33,"nodeOffset":"68.22 -8.24","parent":[6,15,24,27,28,29,30,31,32]},
{"index":34,"nodeOffset":"81.07 -8.24","parent":[7,16,25,27,28,29,30,31,32,33]},
{"index":35,"nodeOffset":"93.92 -8.24","parent":[8,17,26,27,28,29,30,31,32,33,34]},
{"index":36,"nodeOffset":"-65.4 31.25","parent":[0,9,18,27,28,29]},
{"index":37,"nodeOffset":"-9.15 6.25","parent":[1,10,19,27,28,29,36]},
{"index":38,"nodeOffset":"3.7 6.25","parent":[2,11,20,27,28,29,36,37]},
{"index":39,"nodeOffset":"16.56 6.25","parent":[3,12,21,30,31,32,36,37,38]},
{"index":40,"nodeOffset":"29.41 6.25","parent":[4,13,22,30,31,32,36,37,38,39]},
{"index":41,"nodeOffset":"42.26 6.25","parent":[5,14,23,30,31,32,36,37,38,39,40]},
{"index":42,"nodeOffset":"55.11 6.25","parent":[6,15,24,33,34,35,36,37,38,39,40,41]},
{"index":43,"nodeOffset":"67.96 6.25","parent":[7,16,25,33,34,35,36,37,38,39,40,41,42]},
{"index":44,"nodeOffset":"80.81 6.25","parent":[8,17,26,33,34,35,36,37,38,39,40,41,42,43]},
{"index":45,"nodeOffset":"-70.16 45.74","parent":[0,9,18,27,28,29,36,37,38]},
{"index":46,"nodeOffset":"-22.26 20.74","parent":[1,10,19,27,28,29,36,37,38,45]},
{"index":47,"nodeOffset":"-9.41 20.74","parent":[2,11,20,27,28,29,36,37,38,45,46]},
{"index":48,"nodeOffset":"3.44 20.74","parent":[3,12,21,30,31,32,39,40,41,45,46,47]},
{"index":49,"nodeOffset":"16.29 20.74","parent":[4,13,22,30,31,32,39,40,41,45,46,47,48]},
{"index":50,"nodeOffset":"29.14 20.74","parent":[5,14,23,30,31,32,39,40,41,45,46,47,48,49]},
{"index":51,"nodeOffset":"41.99 20.74","parent":[6,15,24,33,34,35,42,43,44,45,46,47,48,49,50]},
{"index":52,"nodeOffset":"54.84 20.74","parent":[7,16,25,33,34,35,42,43,44,45,46,47,48,49,50,51]},
{"index":53,"nodeOffset":"67.69 20.74","parent":[8,17,26,33,34,35,42,43,44,45,46,47,48,49,50,51,52]},
{"index":54,"nodeOffset":"-74.92 60.23","parent":[0,9,18,27,36,45]},
{"index":55,"nodeOffset":"-35.38 35.23","parent":[1,10,19,28,37,46,54]},
{"index":56,"nodeOffset":"-22.53 35.23","parent":[2,11,20,29,38,47,54,55]},
{"index":57,"nodeOffset":"-9.67 35.23","parent":[3,12,21,30,39,48,54,55,56]},
{"index":58,"nodeOffset":"3.18 35.23","parent":[4,13,22,31,40,49,54,55,56,57]},
{"index":59,"nodeOffset":"16.03 35.23","parent":[5,14,23,32,41,50,54,55,56,57,58]},
{"index":60,"nodeOffset":"28.88 35.23","parent":[6,15,24,33,42,51,54,55,56,57,58,59]},
{"index":61,"nodeOffset":"41.73 35.23","parent":[7,16,25,34,43,52,54,55,56,57,58,59,60]},
{"index":62,"nodeOffset":"54.58 35.23","parent":[8,17,26,35,44,53,54,55,56,57,58,59,60,61]},
{"index":63,"nodeOffset":"-79.69 74.72","parent":[0,9,18,27,36,45,54,55,56]},
{"index":64,"nodeOffset":"-48.49 49.72","parent":[1,10,19,28,37,46,54,55,56,63]},
{"index":65,"nodeOffset":"-35.64 49.72","parent":[2,11,20,29,38,47,54,55,56,63,64]},
{"index":66,"nodeOffset":"-22.79 49.72","parent":[3,12,21,30,39,48,57,58,59,63,64,65]},
{"index":67,"nodeOffset":"-9.94 49.72","parent":[4,13,22,31,40,49,57,58,59,63,64,65,66]},
{"index":68,"nodeOffset":"2.91 49.72","parent":[5,14,23,32,41,50,57,58,59,63,64,65,66,67]},
{"index":69,"nodeOffset":"15.76 49.72","parent":[6,15,24,33,42,51,60,61,62,63,64,65,66,67,68]},
{"index":70,"nodeOffset":"28.61 49.72","parent":[7,16,25,34,43,52,60,61,62,63,64,65,66,67,68,69]},
{"index":71,"nodeOffset":"41.46 49.72","parent":[8,17,26,35,44,53,60,61,62,63,64,65,66,67,68,69,70]},
{"index":72,"nodeOffset":"-84.45 89.21","parent":[0,9,18,27,36,45,54,55,56,63,64,65]},
{"index":73,"nodeOffset":"-61.61 64.21","parent":[1,10,19,28,37,46,54,55,56,63,64,65,72]},
{"index":74,"nodeOffset":"-48.75 64.21","parent":[2,11,20,29,38,47,54,55,56,63,64,65,72,73]},
{"index":75,"nodeOffset":"-35.9 64.21","parent":[3,12,21,30,39,48,57,58,59,66,67,68,72,73,74]},
{"index":76,"nodeOffset":"-23.05 64.21","parent":[4,13,22,31,40,49,57,58,59,66,67,68,72,73,74,75]},
{"index":77,"nodeOffset":"-10.2 64.21","parent":[5,14,23,32,41,50,57,58,59,66,67,68,72,73,74,75,76]},
{"index":78,"nodeOffset":"2.65 64.21","parent":[6,15,24,33,42,51,60,61,62,69,70,71,72,73,74,75,76,77]},
{"index":79,"nodeOffset":"15.5 64.21","parent":[7,16,25,34,43,52,60,61,62,69,70,71,72,73,74,75,76,77,78]},
{"index":80,"nodeOffset":"28.35 64.21","parent":[8,17,26,35,44,53,60,61,62,69,70,71,72,73,74,75,76,77,78,79]}
],
"config":{
"algorithm":"Coloring (Backtrack)",
"initialIndexesColoring":"2 0 6 3 0 0 8 9 0\n0 0 0 0 1 0 6 0 0\n0 3 9 0 0 0 0 0 0\n3 0 0 6 2 0 1 0 0\n1 0 0 0 4 0 0 5 0\n0 8 0 0 0 0 0 3 0\n0 4 0 0 0 6 0 0 0\n6 0 0 5 0 0 0 0 8\n8 0 0 0 0 1 0 0 9",
"maxColors":9
}}
6 3 0 9 7 0 0 0 5
7 5 9 0 0 0 0 0 1
0 0 0 0 0 0 0 0 7
0 9 0 0 1 0 0 0 0
0 6 8 3 0 7 0 5 0
0 0 0 0 2 4 0 0 0
0 7 6 4 5 0 0 8 2
3 0 0 0 0 9 0 1 0
1 0 2 0 0 0 5 0 0
-----------------------------
Time: 13 ms
Colores: 1→red, 2→blue, 3→green, 4→yellow,
5→cyan, 6→orange, 7→pink, 8→magenta, 9→lime
Coloring (Backtrack): {"colors":[
6,3,1,9,7,8,4,2,5,
7,5,9,6,4,2,8,3,1,
8,2,4,1,3,5,6,9,7,
4,9,3,5,1,6,2,7,8,
2,6,8,3,9,7,1,5,4,
5,1,7,8,2,4,9,6,3,
9,7,6,4,5,1,3,8,2,
3,4,5,2,8,9,7,1,6,
1,8,2,7,6,3,5,4,9],...Hay que tener en cuenta que un verdadero Sudoku es el que tiene solución única, pues algunas combinaciones de números iniciales pueden dar lugar a más de una solución, como la adjunta que en grafos vemos el resultado obtenido y sin embargo en la aplicación SUDOKU produce dos resultados, como explicamos en el tema sobre unicidad de un Sudoku.
Solución 1:
6 3 1 9 7 8 4 2 5
7 5 9 6 4 2 8 3 1
8 2 4 1 3 5 6 9 7
4 9 3 5 1 6 2 7 8
2 6 8 3 9 7 1 5 4
5 1 7 8 2 4 9 6 3
9 7 6 4 5 1 3 8 2
3 4 5 2 8 9 7 1 6
1 8 2 7 6 3 5 4 9
Solución 2:
6 3 1 9 7 8 4 2 5
7 5 9 6 4 2 8 3 1
8 2 4 1 3 5 9 6 7
4 9 3 5 1 6 2 7 8
2 6 8 3 9 7 1 5 4
5 1 7 8 2 4 6 9 3
9 7 6 4 5 1 3 8 2
3 4 5 2 8 9 7 1 6
1 8 2 7 6 3 5 4 9
La aplicación Sudoku encuentra estas dos soluciones usando también un vuelta atrás, donde la primera solución es la que se alcanza con el coloreado del grafo, observando que la diferencia está en los números resaltados, por lo que no podemos considerarlo un verdadero Sudoku. En cambio el coloreado del grafo con vuelta atrás devuelve siempre la primera solución encontrada sin informar acerca de más soluciones.
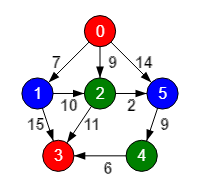
Como hemos dicho al principio de este tema, todos los algoritmos de coloreado de nodos o aristas tratan los grafos dirigidos como no dirigidos. En la Figura vemos que se colorea con 3 colores el grafo dirigido como si fuera no dirigido.
Time: 0 ms
Colores: 1→red, 2→blue, 3→green
Coloreado (Vuelta atrás): {
"colors":[1,2,3,1,3,2],
"partitions":[[0,3],[1,5],[2,4]],
"totalColors":3,
"warnings":[]
}
{"nodes":[
{"index":0,"parent":[{"index":-1}]},
{"index":1,"parent":[{"index":0,"value":7,"lineTextOffset":-0.8}]},
{"index":2,"parent":[{"index":0,"value":9,"lineTextOffset":0.8},{"index":1,"value":10,"lineTextOffset":"0 0.8"}]},
{"index":3,"parent":[{"index":1,"value":15,"lineTextOffset":-0.8},{"index":4,"value":6,"lineTextOffset":"0.5 0.8"},{"index":2,"value":11,"lineTextOffset":0.8}]},
{"index":4,"parent":[{"index":5,"value":9,"lineTextOffset":0.8}]},
{"index":5,"parent":[{"index":0,"value":14,"lineTextOffset":0.8},{"index":2,"value":2,"lineTextOffset":"0 0.8"}]}
],
"config":{
"nodeOffset":"-10",
"markerStart":"arrow",
"algorithm":"Coloring (Backtrack)"
}}
En Wolfram con FindEdgeColoring[g,k] también usa 3 colores aunque dispuestos en otro orden.
g = AdjacencyGraph[{{0,1,1,0,0,1},{0,0,1,1,0,0},{0,0,0,1,0,1},{0,0,0,0,0,0},{0,0,0,1,0,0},{0,0,0,0,1,0}},
ImageSize -> 188, VertexSize -> {"Scaled", 0.1}, VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center],
3 -> Placed[2,Center], 4 -> Placed[3,Center], 5 -> Placed[4,Center], 6 -> Placed[5,Center]}, VertexLabelStyle -> Directive[Black,17.5],
EdgeLabelStyle -> Directive[Black,17.5,Bold], EdgeLabels -> {(1->2)->7, (1->3)->9, (2->3)->10, (2->4)->15, (5->4)->6, (3->4)->11, (6->5)->9, (1->6)->14, (3->6)->2},
VertexStyle -> White, DirectedEdges -> True, EdgeStyle -> {{Black,Thickness[0.005]}}];
k = {Red, Blue, RGBColor["green"], Yellow, Cyan, Orange, Pink, Magenta, Green, Brown, Purple, Gray, Black, RGBColor["lavenderblush"], LightGreen, LightBlue, LightYellow, LightCyan, LightGray};
c = FindVertexColoring[g, k];
d = Flatten[Table[Position[k, i], {i, c}]];
t = Take[{White, White, White, Black, Black, White, Black, White, Black, White, White, White, White, Black, Black, Black, Black, Black, Black}, Length[d]];
s = Table[Directive[t[[i]], 17.5], {i, d}];
v = VertexList[g];
Annotate[g, {VertexStyle->Thread[v->c], VertexLabelStyle->Thread[v->s]}]
VertexChromaticNumber[g]A continuación vemos el JavaScript del algoritmo getColoringBacktrack().
function getColoringBacktrack({matrix=[], initialIndexesColoring=[], maxColors=0}) {
let result = {colors:[], partitions:[], totalColors:0, warnings: []};
try {
let n = matrix.length;
if (initialIndexesColoring.length<n) {
for (let i=initialIndexesColoring.length; i<n; i++) {
initialIndexesColoring.push(0);
}
} else if (initialIndexesColoring.length>n) {
initialIndexesColoring = initialIndexesColoring.slice(0, n);
}
function backtrack({matrix=[], index=0, maxColors=0, colors=[]}) {
if (iter++, iter>maxIter*1000) return `Maximum iterations '${maxIter}' reached`;
let n = matrix.length;
if (index===-1) {
return true;
} else {
for (let color=1; color<=maxColors; color++) {
let isPossible = true;
for (let i=0; i<n; i++) {
if (i!==index && (matrix[index][i]!==0 || matrix[i][index]!==0) && colors[i]===color){
isPossible = false;
break;
}
}
if (isPossible) {
colors[index] = color;
let j = colors.findIndex(v => v===0);
if (backtrack({matrix, index:j, maxColors, colors})) {
return true;
}
colors[index] = 0;
}
}
}
return false;
}
let index = initialIndexesColoring.findIndex(v => v===0);
if (index>-1) {
let [from, to] = maxColors===0 ? [1, n] : [maxColors, maxColors];
for (let m=from; m<=to; m++) {
let colors = [...initialIndexesColoring];
iter = 0;
let ok = backtrack({matrix, index, maxColors:m, colors});
if (typeof ok==="string") {
result.warnings.push(ok);
result.colors = colors;
break;
} else if (ok) {
if (colors.some(v => v===0)) {
result.warnings.push(`Some color is 0 and more iterations may be needed`)
}
result.colors = colors;
break;
}
}
}
if (result.colors.length===0 || result.colors.some(v => v===0)) {
if (maxColors>0) {
result.warnings.push(`The graph cannot be colored with '${maxColors}' colors`)
} else {
result.warnings.push(`Could not color graph with '${maxIter}' iterations`)
}
} else if (result.warnings.length===0) {
result.totalColors = Math.max(...result.colors);
result.partitions = Array.from({length:result.totalColors}, ()=>[]);
for (let i=0; i<result.colors.length; i++){
result.partitions[result.colors[i]-1].push(i);
}
}
} catch(e) {result = e.message}
return result;
}En los temas vuelta atrás y sudoku con vuelta atrás expusimos unos esquemas de código o pseudocódigo parar entender el funcionamiento del algoritmo vuelta atrás. En aquellos temas se encontraban todas las soluciones, mientras que en nuestro algoritmo sólo nos interesa la primera. Reescribimos el pseudocódigo de la siguiente forma, pero en el fondo se trata del mismo planteamiento:
Create empty item
Function backtrack(item)
If item is solution
Return item
Else
Define choices for this item
For choice of choices
If item with choice is possible
Build item with choice
backtrack(item)
Undo item
End If
End For
End If
End Function
backtrack(item)Un ítem es un ejemplar de una posible solución y un índice de nodo a gestionar. Para nuestro caso es la lista de colores colors con tantas posiciones con cero como nodos tenga el grafo, que será una solución si todas las posiciones son mayores que cero, lo que equivale a gestionar un índice -1, puesto que es indicativo de que ya esa lista contiene todos los nodos del grafo.
Si ese ítem no es solución definimos todas las posibles elecciones (choices) para un nuevo item, que en nuestro caso son los colores disponibles entre 1 y maxColors. Por cada elección (choice), es decir, para cada color vemos si es posible para ese nodo de tal forma que sus nodos vecinos no tengan el mismo color. En caso de ser posible incluimos ese color en la lista de colores colors y elegimos el siguiente nodo aún no coloreado, con una nueva llamada al vuelta atrás. Si en el curso de todas las llamadas llegamos a una solución se devuelve. En otro caso se deshace esa acción volviendo a un punto anterior y se intenta con otro color.

En un vuelta atrás siempre hay implícito una búsqueda en un árbol. Tomemos como ejemplo el coloreado del grafo de la Figura en el que vamos a ejecutar el algoritmo getColoringBacktrack() con la opción máximo número colores igual a 3. En la Figura vimos que trazado era una de las opciones para ejecutar el algoritmo. Marcando esa opción para ese grafo obtenemos este resultado, con una traza en el campo "trace":
Time: 0 ms
Colores: 1→red, 2→blue, 3→green
Coloring (Backtrack): {
"colors":[1,2,3,1,3,1,2,1,1],
"partitions":[[0,3,5,7,8],[1,6],[2,4]],
"totalColors":3,
"warnings":[],
"trace":[
"[1,0,0,0,0,0,0,0,0]",
"[1,2,0,0,0,0,0,0,0]",
"[1,2,1,0,0,0,0,0,0]",
"[1,2,1,2,0,0,0,0,0]",
"[1,2,1,2,3,0,0,0,0]",
"Undo [1,2,1,2,0,0,0,0,0]",
"Undo [1,2,1,0,0,0,0,0,0]",
"[1,2,1,3,0,0,0,0,0]",
"[1,2,1,3,3,0,0,0,0]",
"Undo [1,2,1,3,0,0,0,0,0]",
"Undo [1,2,1,0,0,0,0,0,0]",
"Undo [1,2,0,0,0,0,0,0,0]",
"[1,2,3,0,0,0,0,0,0]",
"[1,2,3,1,0,0,0,0,0]",
"[1,2,3,1,3,0,0,0,0]",
"[1,2,3,1,3,1,0,0,0]",
"[1,2,3,1,3,1,2,0,0]",
"[1,2,3,1,3,1,2,1,0]",
"[1,2,3,1,3,1,2,1,1]"
]
}
Cada entrada en "trace" es un nodo de un árbol que representamos en la Figura, con cada nodo como la lista de colores colors de las que prescindimos de las comas para abreviar. El nodo raíz del árbol empieza por adjudicar el color número 1 al índice 0 de esa lista, es decir, al nodo 0 del grafo.
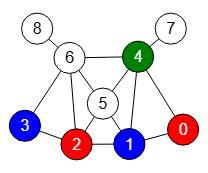
El árbol del vuelta atrás discurre de arriba a abajo y de izquierda a derecha. La primera rama llega hasta la lista de colores [1,2,1,2,3,0,0,0,0] sin posibilidad de éxito, pues al colorear el nodo "4" con color verde (color 3) no podremos colorear el siguiente nodo 5 con rojo, azul o verde (colores 1,2,3) pues tiene como vecinos esos colores, recordando que imponemos que el grafo debe ser coloreado con 3 colores. Así que hay que deshacer los últimos coloreados hasta llegar a una posición que permite una elección (choice) diferente.
Vemos que en la rama de la derecha del árbol puede completar el coloreado. Un vuelta atrás siempre tendrá éxito, en caso de que exista solución, que para nuestro ejemplo es que se pueda colorear ese grafo con 3 colores que sabemos previamente que es posible. Con grafos con muchos nodos puede resultar muy costoso recorrer ese árbol si la solución está muy abajo y a la derecha de ese árbol implícito. Y si no tiene solución tendrá que recorrer todo el árbol completo.
Con este JSON puede importar el ejemplo:
{"nodes":[
{"index":0,"nodeOffset":"23.27 39.56","parent":-1},
{"index":1,"nodeOffset":"18.45 20.36","parent":0},
{"index":2,"nodeOffset":"5.63 -4.52","parent":1},
{"index":3,"nodeOffset":"-23.36 -36.99","parent":2},
{"index":4,"nodeOffset":"-11.42 -14.72","parent":[0,1]},
{"index":5,"nodeOffset":"-8.82 -20.88","parent":[1,2,4]},
{"index":6,"nodeOffset":"-38.83 -64.25","parent":[2,3,4,5]},
{"index":7,"nodeOffset":"-6.66 -50.99","parent":4},
{"index":8,"nodeOffset":"-35.13 -100.99","parent":6}
],
"config":{
"algorithm":"Coloring (Backtrack)",
"maxColors":3,
"tracing":true
}}Y con este JSON el árbol de búsqueda del vuelta atrás:
{"nodes":[
{"index":0,"value":100000000,"nodeOffset":"29 -2.5","parent":-1},
{"index":1,"nodeOffset":"29 -2.5","value":120000000,"parent":0},
{"index":2,"nodeOffset":"15.67 -6.4","value":121000000,"parent":1},
{"index":3,"nodeOffset":"2.2 -10.5","value":121200000,"parent":2},
{"index":4,"nodeOffset":"-6 -9.5","value":121230000,"parent":3},
{"index":5,"nodeOffset":"17 -10.5","value":121300000,"parent":2},
{"index":6,"nodeOffset":"17 -9.5","value":121330000,"parent":5},
{"index":7,"nodeOffset":"45.33 -6.64","value":123000000,"parent":1},
{"index":8,"nodeOffset":"37 -10.5","value":123100000,"parent":7},
{"index":9,"nodeOffset":"37 -9.5","value":123130000,"parent":8},
{"index":10,"nodeOffset":"62 -10.6","value":123131000,"parent":9},
{"index":11,"nodeOffset":"62 -14.4","value":123131200,"parent":10},
{"index":12,"nodeOffset":"62 -17.8","value":123131210,"parent":11},
{"index":13,"nodeOffset":"62 -21.6","value":123131211,"parent":12}
],
"config":{
"lineHeight":21.25,
"nodeBorderColor":"white"
}}Coloreado aristas de un grafo getColoringEdges()

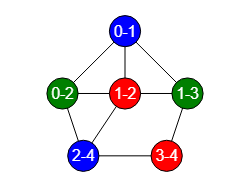
El coloreado de aristas de un grafo se basa en que todas las aristas que inciden en un nodo deben tener color diferente. Por ejemplo, las tres aristas que inciden en el nodo "1" de la Figura tienen colores diferentes.
El algoritmo getColoringEdges() nos devuelve el siguiente resultado para ese grafo, donde las entradas en el campo "colors" son como la primera [[0,1],2] que se refiere a que la arista "0-1" tiene color número 2, que según la lista de colores que se pasa al algoritmo se indexa con el color azul.
Time: 1 ms
Colores: 1→red, 2→blue, 3→green, 4→yellow, 5→cyan, 6→orange
Coloreado aristas (welsh-powell): {
"colors":[[[0,1],2], [[0,2],3], [[1,2],1], [[1,3],3], [[2,4],2], [[3,4],1]],
"totalColors":3,
"warnings":[]
}
{"nodes":[
{"index":0,"parent":[{"index":-1}]},
{"index":1,"parent":[{"index":0}]},
{"index":2,"parent":[{"index":0},{"index":1}]},
{"index":3,"parent":[{"index":1},{"index":4}]},
{"index":4,"parent":[{"index":2}]}
],
"config":{
"nodeOffset":"-20",
"algorithm":"Coloring edges",
"methodColoring":"welsh-powell"
}}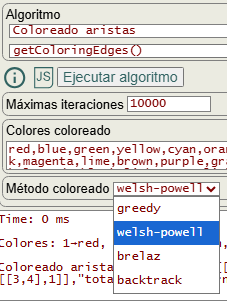
En la Figura vemos las opciones para ejecutar el algoritmo, pasando en colores coloreado una lista de colores a utilizar y método coloreado puede ser alguno de "greedy, welsh-powell, brelaz, backtrack" que vimos en apartados anteriores para colorear los nodos de un grafo. Pues para colorear las aristas vamos a colorear los nodos del grafo línea del grafo inicial.
La operación grafo línea sobre un grafo no dirigido G genera otro grafo línea L(G) donde sus nodos representan las aristas del grafo original G y donde cada dos nodos del grafo línea L(G) son adyacentes si y sólo si comparten un vértice común en el grafo original G.
Y colorear las aristas de un grafo equivale a colorear los nodos de su grafo línea, como hemos dicho.
{"error":"",
"matrix":
[[0,1,1,1,0,0],
[1,0,1,0,1,0],
[1,1,0,1,1,0],
[1,0,1,0,0,1],
[0,1,1,0,0,1],
[0,0,0,1,1,0]],
"vertexs":
["0-1","0-2","1-2",
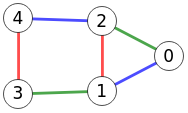
"1-3","2-4","3-4"]}En la Figura vemos el grafo línea del grafo del ejemplo de la Figura, con 6 nodos, tantos como aristas de ese grafo inicial. Las etiquetas de los nodos identifican las aristas del grafo inicial, como vemos en el resultado de esa operación, devolviendo la matriz de adyacencia del grafo línea y de las etiquetas de los nodos en "vertexs".
Entonces coloreamos los nodos de este grafo línea con el algoritmo coloringWelshPowell(), método que se pasó al algoritmo en este ejemplo, con el siguiente resultado, a partir del cual finalmente trasladamos los colores de los nodos de este grafo línea a las aristas del grafo inicial que resulta en el de la Figura.
Time: 1 ms
Colores: 1→red, 2→blue, 3→green
Coloreado (Welsh Powell): {
"colors":[2,3,1,3,2,1],
"partitions":[[2,5],[0,4],[1,3]],
"totalColors":3
}Este es el JSON del grafo línea:
{"nodes":[
{"index":0,"value":"0-1","parent":[{"index":-1}]},
{"index":1,"value":"0-2","parent":[{"index":0}]},
{"index":2,"value":"1-2","parent":[{"index":0},{"index":1}]},
{"index":3,"value":"1-3","parent":[{"index":0},{"index":2}]},
{"index":4,"value":"2-4","parent":[{"index":1},{"index":2}]},
{"index":5,"value":"3-4","parent":[{"index":3},{"index":4}]}
],
"config":{
"algorithm":"Coloring (Welsh Powell)"
}}
En la Figura vemos que Wolfram alcanza el mismo resultado usando la función FindEdgeColoring[g, k], donde "k" es una lista de colores.
g = AdjacencyGraph[{{0,1,1,0,0},{1,0,1,1,0},{1,1,0,0,1},{0,1,0,0,1},{0,0,1,1,0}},
ImageSize -> 188, VertexSize -> {"Scaled", 0.17}, VertexLabels -> {1 -> Placed[0,Center],
2 -> Placed[1,Center], 3 -> Placed[2,Center], 4 -> Placed[3,Center], 5 -> Placed[4,Center]},
VertexLabelStyle -> Directive[Black,17.5], EdgeLabelStyle -> Directive[Black,17.5,Bold],
VertexStyle -> White, EdgeStyle -> {{Black,Thickness[0.005]}}];
k = {Red, Blue, RGBColor["green"], Yellow, Cyan, Orange, Pink, Magenta, Green, Brown, Purple, Gray, Black, RGBColor["lavenderblush"], LightGreen, LightBlue, LightYellow, LightCyan, LightGray};
c = FindEdgeColoring[g, k];
Annotate[g, {EdgeStyle->Thread[EdgeList[g]->c], EdgeStyle->Thickness[0.015]}]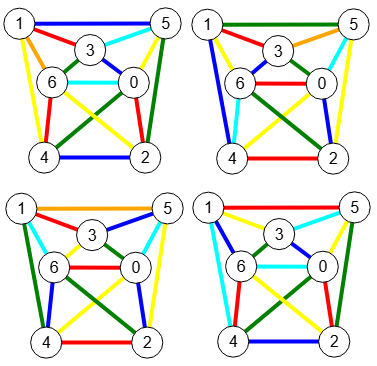
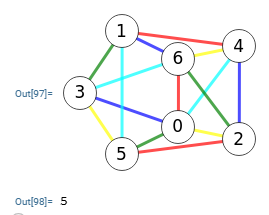
Coloreando las aristas del grafo de la Figura con los cuatro algoritmos greedy, Welsh-Powell, Brelaz y backtracking vemos que los tres primeros usan 6 colores (rojo, azul, verde, amarillo, cyan y naranja) mientras que el último sólo necesita 5 colores. El vuelta atrás o backtracking siempre encuentra el mínimo número de colores por lo que 5 es el índice cromático de ese grafo. El índice cromático siempre es igual o menor que el mayor grado de los vértices más uno. Vemos que los nodos "0" y "6" son los de mayor grado 5, así que el índice cromático será igual o menor que 5+1=6.
{"nodes":[
{"index":0,"nodeOffset":"23.97 24.36","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"-55.28 0.65","parent":[{"index":-1}]},
{"index":2,"nodeOffset":"45.24 29.42","parent":[{"index":0}]},
{"index":3,"nodeOffset":"6.46 -13.77","parent":[{"index":0},{"index":1}]},
{"index":4,"nodeOffset":"-28.64 29.42","parent":[{"index":0},{"index":1},{"index":2}]},
{"index":5,"nodeOffset":"3.42 -24.49","parent":[{"index":0},{"index":1},{"index":2},{"index":3}]},
{"index":6,"nodeOffset":"-58.77 -0.78","parent":[{"index":0},{"index":1},{"index":2},{"index":3},{"index":4}]}
],
"config":{
"algorithm":"Coloring edges",
"methodColoring":"backtrack"
}}
Wolfram también colorea las aristas con 5 colores. Si agregamos la línea EdgeChromaticNumber[g] nos devolverá el índice cromático 5.
g = AdjacencyGraph[{{0,0,1,1,1,1,1},{0,0,0,1,1,1,1},{1,0,0,0,1,1,1},{1,1,0,0,0,1,1},{1,1,1,0,0,0,1},{1,1,1,1,0,0,0},{1,1,1,1,1,0,0}},
ImageSize -> 200, VertexSize -> {"Scaled", 0.16}, VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center], 3 -> Placed[2,Center],
4 -> Placed[3,Center], 5 -> Placed[4,Center], 6 -> Placed[5,Center], 7 -> Placed[6,Center]}, VertexLabelStyle -> Directive[Black,17.5],
EdgeLabelStyle -> Directive[Black,17.5,Bold], VertexStyle -> White, EdgeStyle -> {{Black,Thickness[0.005]}}];
k = {Red, Blue, RGBColor["green"], Yellow, Cyan, Orange, Pink, Magenta, Green, Brown, Purple, Gray, Black, RGBColor["lavenderblush"], LightGreen, LightBlue, LightYellow, LightCyan, LightGray};
c = FindEdgeColoring[g, k];
Annotate[g, {EdgeStyle->Thread[EdgeList[g]->c], EdgeStyle->Thickness[0.015]}]
EdgeChromaticNumber[g]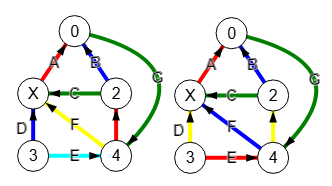
El coloreado de aristas en un grafo dirigido ignorará las direcciones considerando el grafo como no dirigido, tal como vimos para el coloreado de nodos. El grafo de la izquierda de la Figura es el coloreado con 5 colores con greedy y Welsh-Powell, mientras que el de la derecha tiene 4 colores con Brelaz y backtrack.
Time: 0 ms
Colores: 1→red, 2→blue, 3→green, 4→yellow, 5→cyan, 6→orange, 7→pink, 8→magenta
Coloreado aristas (backtrack): {
"colors":[[[0,1],1],[[0,2],2],[[0,4],3],[[1,2],3],
[[1,3],4],[[1,4],2],[[2,4],4],[[3,4],1]],
"totalColors":4,"warnings":[]}
{"nodes":[
{"index":0,"parent":-1},
{"index":1,"value":"X","parent":[{"index":0,"value":"A"}]},
{"index":2,"parent":[{"index":0,"value":"B"},{"index":1,"value":"C"}]},
{"index":3,"parent":[{"index":1,"value":"D","lineTextOffset":"-0.75 0.25"},{"index":4,"value":"E"}]},
{"index":4,"parent":[{"index":1,"value":"F"},2,{"index":0,"lineOffset":"8 -2","markerReverse":true,"lineType":"quadratic","value":"G"}]}
],
"config":{
"nodeOffset":"-20",
"markerEnd":"arrow",
"algorithm":"Coloring edges",
"methodColoring":"backtrack"
}}
Wolfram también ignora direcciones y colorea con 4 colores siendo ese el índice cromático del grafo.
g = AdjacencyGraph[{{0,0,0,0,1},{1,0,0,0,0},{1,1,0,0,0},{0,1,0,0,1},{0,1,1,0,0}}, ImageSize -> 188,
VertexSize -> {"Scaled", 0.17}, VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed["X",Center],
3 -> Placed[2,Center], 4 -> Placed[3,Center], 5 -> Placed[4,Center]}, VertexLabelStyle -> Directive[Black,17.5],
EdgeLabelStyle -> Directive[Black,17.5,Bold], EdgeLabels -> {(2->1)->"A", (3->1)->"B", (3->2)->"C",
(4->2)->"D", (4->5)->"E", (5->2)->"F", (1->5)->"G"}, VertexStyle -> White, DirectedEdges -> True,
EdgeStyle -> {{Black,Thickness[0.005]}}];
k = {Red, Blue, RGBColor["green"], Yellow, Cyan, Orange, Pink, Magenta, Green, Brown, Purple, Gray, Black, RGBColor["lavenderblush"], LightGreen, LightBlue, LightYellow, LightCyan, LightGray};
c = FindEdgeColoring[g, k];
Annotate[g, {EdgeStyle->Thread[EdgeList[g]->c], EdgeStyle->Thickness[0.015]}]
EdgeChromaticNumber[g]Se muestra a continuación el JavaScript de getColoringEdges() usando la operación operateLineGraph(). El coloreado de nodos y aristas siempre gestiona los grafos como no dirigidos, pero la operación grafo línea devuelve un resultado distinto si es dirigido o no dirigido, con lo que tenemos que saber si es dirigido con isGraphDirected() para convertirlo a no dirigido con la operación operateDirectionGraph().
function getColoringEdges({matrix=[], methodColoring="greedy"}) {
let result = {colors:[], totalColors:0, warnings:[]}, temp;
try {
if (temp = isGraphDirected({matrix}), typeof temp==="string") throw new Error(temp);
if (temp) {
if (temp = operateDirectionGraph({matrix, edgesDirection:"undirected"}), temp.error) throw new Error(temp.error);
matrix = temp.matrix;
}
if (temp = operateLineGraph({matrix}), temp.error) throw new Error(temp);
let lineMatrix = temp.matrix;
let vertexs = temp.vertexs;
let method = methodColoring.replace(/([a-z])\-([a-z])/g, (b0,b1,b2) => `${b1}${b2.toUpperCase()}`);
method = "getColoring" + method[0].toUpperCase() + method.substring(1);
let keys = Object.keys(algorithms);
let k = keys.findIndex(v => algorithms[v].name===method);
if (k>-1) {
let func = algorithms[keys[k]];
if (temp = func({matrix:lineMatrix}), typeof temp==="string") throw new Error(`${method}(): ` + temp);
let colors = temp.colors;
if (temp.hasOwnProperty("warnings") && temp.warnings.length>0) result.warnings.push(...temp.warnings);
for (let i=0; i<colors.length; i++) {
let [u, v] = vertexs[i].split("-").map(w => +w);
result.colors.push([[u,v], colors[i]]);
}
result.totalColors = Math.max(...colors);
}
} catch(e) {result = e.message}
return result;
}