Corte de aristas Karger-Stein
Encontrar corte mínimo aristas Karger findEdgeCutKarger()
El algoritmo de Karger es un procedimiento probabilista para encontrar el corte mínimo de aristas de un grafo no dirigido y conectado. Un algoritmo es probabilista si en el resultado intervienen decisiones que se toman al azar. A diferencia del algoritmo determinista que siempre devuelve el mismo resultado con los mismos datos de entrada, el algoritmo probabilista puede devolver distintas soluciones.
En temas anteriores vimos los algoritmos findEdgeCut() y findEdgeCutGomoryHu() para encontrar los cortes mínimos de aristas de un grafo. Ambos hacían uso de findSTEdgeCut() para encontrar el corte mínimo entre "s" y "t". El segundo además hacía uso del árbol Gomory-Hu que había que construir previamente haciendo uso también de la operación operateContractionGraph() para contraer dos nodos del grafo.
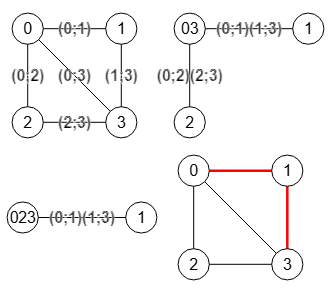
El algoritmo de Karger hace uso sólo de la operación contracción, contrayendo aristas sucesivamente hasta que solo queden dos nodos en cuyo caso ya sólo queda un único corte. Inicialmente todas las aristas de un grafo con los nodos {u, v, w, ...} se etiquetan como texto (string), por ejemplo "(u;v)". Al contraer una arista usando la opción suma para el valor fusionado se concatenan estas etiquetas al ser texto y tendremos al final en la arista resultante una secuencia de etiquetas como "(u;v)(w;x)...(x;y)" que convertiremos en una lista de aristas de corte, tal como se observa en el primer grafo de la Figura, imagen que resumen el proceso de etiquetado y contracción de aristas para la obtención del grafo final con un corte mínimo de aristas, proceso que explicaremos después.
Encontrar corte aristas Karger: {
"edges":[[0,1],[1,3]],
"length":2,
"repetitions":100,
"successProbability":0.9999999879253265,
"contractions":200}La aplicación devuelve un objeto resultado con "edges" que son las aristas de mínimo corte devolviendo [[0,1],[1,3]] que vemos en la Figura, "length" la longitud de esa lista de aristas, "repetitions" el número de repeticiones del algoritmo, "successProbability" la probabilidad de éxito y "contractions" el número de contracciones que se ha realizado. Con el siguiente JSON puede importar el ejemplo.
{"nodes":[
{"index":0,"nodeOffset":"-32.5 5","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"30 -20","parent":[{"index":0}]},
{"index":2,"nodeOffset":"-32.5 17.5","parent":[{"index":0}]},
{"index":3,"nodeOffset":"-20 17.5","parent":[{"index":0},{"index":2},{"index":1}]}
],
"config":{
"algorithm":"Find edge cut Karger"
}}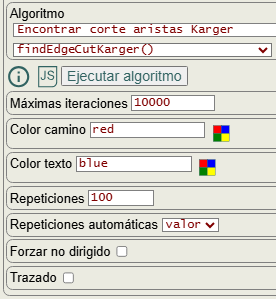
En las opciones para ejecutar el algoritmo vemos en la Figura la opción repeticiones que se establece por defecto en 100. La opción repeticiones automáticas, que explicaremos más abajo, viene con "valor" por defecto aplicándose las que se impongan en la opción anterior. La opción forzar no dirigido tratará el grafo como no dirigido, pues el algoritmo de Karger sólo aplica a no dirigidos. Las opciones color camino y color texto se aplican tras ejecutarse el algoritmo con objeto de presentar gráficamente el resultado.
La opción trazado devuelve los pasos de las contracciones para estudiar su comportamiento, obteniéndose lo siguiente en el ejemplo anterior, donde al inicio esta la matriz original tras reetiquetar las aristas de la forma "(u;v)" como hemos comentado. Esta matriz reetiquetada está en modo valores null/value que en la aplicación permite valores de aristas con texto, mientras que las posiciones sin aristas se indican con valor null de JavaScript.
[[null,"(0;1)","(0;2)","(0;3)"],
["(0;1)",null,null,"(1;3)"],
["(0;2)",null,null,"(2;3)"],
["(0;3)","(1;3)","(2;3)",null]],
{
"s":0,
"t":3,
"matrix":
[[null,"(0;1)(1;3)","(0;2)(2;3)"],
["(0;1)(1;3)",null,null],
["(0;2)(2;3)",null,null]],
"labels":[[0,3],[1],[2]]
},
{
"s":0,
"t":2,
"matrix":
[[null,"(0;1)(1;3)"],
["(0;1)(1;3)",null]],
"labels":[[0,2],[1]]
}
Antes de explicar la traza anterior, veamos la operación operateContractionGraph() para contraer dos nodos del grafo, entre los cuales puede haber o no una arista. En la Figura vemos el mismo grafo del ejemplo donde contraemos los nodos "s=0" y "t=3" con una arista entre ellos, utilizando la operación suma para los valores fusionados. Cuando el grafo no tiene valores en las aristas se entienden que tienen valor númerico unitario. La operación contracción toma las aristas "0-1" y "3-1" y las convierte en la arista "0-1" fusionando con la suma 1+1=2 de los dos valores unitarios de esas dos aristas. Y lo mismo hace con las aristas "0-2" y "3-2". Con la opción de no omitir autobucles, la arista "0-3" entre los dos nodos a contraer se convierte en un autobucle.
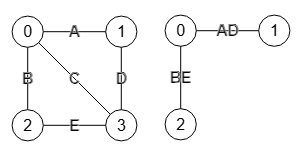
En la Figura tenemos el mismo grafo pero etiquetando las aristas con letras. Contraemos la arista "0-3" pero omitiendo autobucles. Usamos la misma operación suma, que al ser texto se concatenan, observando que la arista "0-3" con valor "C" desaparece pues omitimos autobucles. Esta eliminación de la arista que se contrae es importante pues más abajo explicaremos que es la base de este algoritmo.
A continuación vemos el JSON y la matriz de adyacencia del grafo anterior. Observe la matriz en modo valor null/value, donde las posiciones con valor null significa que no hay arista y si es distinto de nulo significa el valor de la arista, valores que pueden ser un número o un texto. Recordemos que los otros modos de valores posibles son "0/1" donde no aparece ningún valor en las aristas, "0/number" para grafos ponderados y "false/true" que es equivalente a "0/1".
{"nodes":[
{"index":0,"nodeOffset":"-32.5 5","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"30 -20","parent":[{"index":0,"value":"A"}]},
{"index":2,"nodeOffset":"-32.5 17.5","parent":[{"index":0,"value":"B"}]},
{"index":3,"nodeOffset":"-20 17.5","parent":[{"index":0,"value":"C"},{"index":2,"value":"E"},{"index":1,"value":"D"}]}
],
"config":{}}
[[null, "A", "B", "C"],
["A", null, null, "D"],
["B", null, null, "E"],
["C", "D", "E", null]]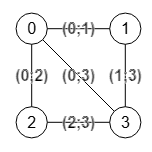
Explicado lo anterior, pasamos ahora a ver el ejemplo. Ya dijimos que el algoritmo de Karger sólo puede aplicarse a grafos no dirigidos y conectados, pero además se van a ignorar los valores de las etiquetas iniciales. Recordemos que todos los algoritmos se ejecutan recibiendo de entrada una matriz de adyacencia. El primer paso entonces es hacer un copia de esa matriz y etiquetar las aristas como se observa en la Figura, identificando la arista entre nodos "u" y "v" con la etiqueta de texto "(u;v)".
{"nodes":[
{"index":0,"nodeOffset":"-32.5 5","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"30 -20","parent":[{"index":0,"value":"(0;1)"}]},
{"index":2,"nodeOffset":"-32.5 17.5","parent":[{"index":0,"value":"(0;2)"}]},
{"index":3,"nodeOffset":"-20 17.5","parent":[{"index":0,"value":"(0;3)"},{"index":1,"value":"(1;3)"},{"index":2,"value":"(2;3)"}]}
],
"config":{}}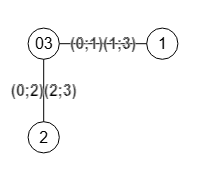
El algoritmo de Karger seleccionar en cada paso aleatoriamente una arista del grafo. En la traza vemos que seleccionó la arista "0-3".
"s":0, "t":3, "matrix": [[null,"(0;1)(1;3)","(0;2)(2;3)"], ["(0;1)(1;3)",null,null], ["(0;2)(2;3)",null,null]], "labels":[[0,3],[1],[2]]
Contraemos entonces los nodos "0" y "3" omitiendo autobucles y con la operación suma que, para texto, es la concatenación de las etiquetas. Observe que la operación de contracción devuelve la etiqueta "labels":[[0,3],[1],[2]] que permite la correspondencia entre los nuevos nodos del grafo contraído y los nodos iniciales, observando que 0≡[0,3], 1≡[1], 2≡[2]
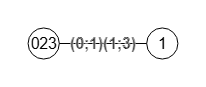
En la traza vemos que en el siguiente paso el algoritmo seleccionó aleatoriamente la arista "0-2", entendiendo estos índices "0" y "2" sobre el grafo contraído en el paso anterior, donde el nodo "0" equivale al "[0,3]" inicial y el "2" al "[2]" inicial.
"s":0, "t":2, "matrix": [[null,"(0;1)(1;3)"], ["(0;1)(1;3)",null]], "labels":[[0,2],[1]]
En la Figura vemos el grafo contrayendo la arista "0-2", con la correspondencia de etiquetas 0≡[0,2], 1≡[1]. Resolviendo la correspondencia en el paso anterior queda finalmente 0≡[0,2,3], 1≡[1]
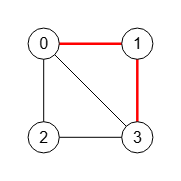
Cuando en el algoritmo de Karger llegamos a un grafo contraído con dos nodos como el de la Figura habremos finalizado, teniendo en la etiqueta de la única arista un corte del grafo. Convertimos esa etiqueta "(0;1)(1;3)" en Array con [[0,1],[1,3]] representando el corte de tamaño 2 de las aristas "0-1" y "1-3", corte que vemos en la Figura.
Observando el grafo de la Figura vemos que hay seis cortes posibles para separar el grafo en dos componentes conectados, dos cortes de tamaño 2 aristas que son "0-1, 1-3" y "0-2, 2-3" y cuatro de tamaño 3 aristas que son "0-1, 0-2, 0-3"; "3-1, 3-0, 3-2"; "0-1, 0-3, 2-3"; "0-2, 0-3, 1-3". Hay más cortes pero separan el grafo en más de dos componentes conectados. Seleccionando aristas aleatoriamente como vimos antes podemos obtener alguno de estos cortes, aunque luego veremos el motivo de que el algoritmo devuelva alguno de los cortes mínimos.
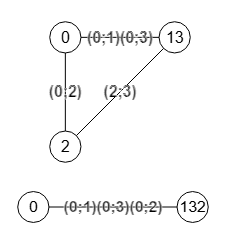
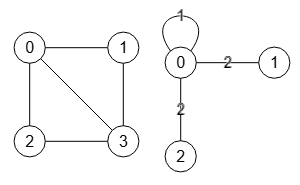
Supongamos que el algoritmo de Karger selecciona aleatoriamente la arista "1-3" para contraer en el grafo inicial anterior, quedando el grafo contraído como el superior de la Figura. Y que en el siguiente paso selecciona "1-2" que se corresponde con "13-2" del grafo contraído anterior quedando como el inferior de la Figura. Habremos finalizado con solo dos nodos donde la etiqueta final "(0;1)(0;3)(0;2)" convertida a Array [[0,1],[0,3],[0,2]] es uno de los cortes de tamaño 3 aristas que tiene el grafo, no siendo por tanto un corte mínimo.
Probabilidad de obtener un corte mínimo al contraer aristas repetidamente
Cortes de tamaño 2 [0,1],[1,3] [0,2],[2,3] Cortes de tamaño 3 [0,3],[1,3],[2,3] [0,1],[0,3],[2,3] [0,1],[0,2],[0,3] [0,2],[0,3],[1,3]
Recordemos que el grafo del ejemplo anterior tiene dos cortes de tamaño 2 y cuatro de tamaño 3. Vimos que en una ejecución de las contracciones podemos obtener alguno de esos 6 cortes, con lo que podríamos obtener cortes de tamaño 3 que no son mínimos. Podríamos ejecutar las contracciones repetidas veces, dígamos un número razonablemente grande de veces y guardar el primer corte mínimo que encontremos. Ese número de repeticiones debe ser tal que asegure una alta probabilidad de encontrar un corte mínimo.
Esto es factible pues en un grafo hay más cortes de aristas no mínimos que mínimos, con lo que la elección aleatoria de aristas tiene más probabilidad de seleccionar aquellas que no son de corte mínimo, quedando estas al final. Este es el planteamiento básico del algoritmo de Karger.
En el ejemplo anterior tenemos una proporción de 2/6=0.33 de aristas de corte mínimo y 4/6=0.67 de corte no mínimo, por lo que la probabilidad de seleccionar aristas de un corte no mínimo en las contracciones son superiores, con más probabilidad de que las de corte mínimo se queden al final sin contraer.
Supongamos que ese número de repeticiones es 100. En la Figura vimos las opciones repeticiones con valor 100, significando que se repiten 100 veces el proceso de contracciones partiendo de un copia del grafo inicial hasta alcanzar un grafo con dos nodos, como vimos antes. La aplicación permite trazar también la distribución de los resultados obtenidos.
"[0,2],[2,3]":26, "[0,1],[1,3]":20, "[0,2],[0,3],[1,3]":11, "[0,1],[0,2],[0,3]":11, "[0,1],[0,3],[2,3]":18, "[0,3],[1,3],[2,3]":14 "[0,1],[1,3]":31, "[0,2],[0,3],[1,3]":15, "[0,2],[2,3]":28, "[0,3],[1,3],[2,3]":9, "[0,1],[0,2],[0,3]":8, "[0,1],[0,3],[2,3]":9 "[0,2],[0,3],[1,3]":18, "[0,1],[0,3],[2,3]":15, "[0,1],[0,2],[0,3]":17, "[0,2],[2,3]":19, "[0,3],[1,3],[2,3]":16, "[0,1],[1,3]":15
En estos datos vemos 3 ejecuciones del algoritmo observando la distribución de cada corte. Como se hace con 100 repeticiones en cada ejecución, esos números pueden verse como porcentajes. Vemos que en la primera ejecución hay 26+20=46% para los dos cortes mínimos, en la segunda 31+28=59% y en la tercera 19+15=34%.
Obviamente como hay 6 cortes la probabilidad de obtener como resultado cada corte es de 1/6 ≃ 16.67% observando por ejemplo que los datos de la de las tres ejecuciones tienen una media de 16.67 que coincide con esa probabilidad. Por ejemplo, la última M = {18, 15, 17, 19, 16, 15} se distribuyen con esa media de 16.67 y una desviación estándar de 1.633 menor que las otras, como puede observar en Wolfram Alpha.
Nos planteamos cuál es el mínimo número de repeticiones del algoritmo que hay que ejecutar para asegurarnos con una alta probabilidad que encontraremos un corte mínimo. Si un evento tiene una probabilidad de éxito p=1/6 y llevo a cabo t=100 pruebas, la probabilidad de éxito de que se obtenga al menos una vez ese evento es:
Vea que si la probabilidad de éxito de un evento es p la de fracaso es 1-p. La probabilidad de fracaso en t pruebas sería (1-p)t y obtener al menos un éxito en t pruebas es el complemento de no tener ningún éxito 1-(1-p)t
Encontrar corte aristas Karger: {
"edges":[[0,1],[1,3]],
"length":2,
"repetitions":100,
"successProbability":0.9999999879253265,
"contractions":200Esta probabilidad de éxito 0.9999999879... es la que vimos en el resultado obtenido en la aplicación y que reproducimos otra vez aquí, observando que se ejecutaban 100 repeticiones. Vemos que en total se hicieron 200 contracciones, pues tal como vimos en el apartado anterior, necesitábamos 2 contracciones en cada ejecución. Esa probabilidad es a efectos prácticos del 100%, por lo que podríamos reducir el número de pruebas asegurando una probabilidad no tan excesivamente alta. Por ejemplo, ejecutando sólo 15 pruebas obtenemos 1-(1-1/6)15 = 0.935···, es decir, una probabilidad de éxito superior al 93.5%.
Si un grafo tiene pocos nodos como este ejemplo, ejecutar 100 repeticiones no supone mucha carga, pero con muchos nodos tenemos que plantearnos ese número de repeticiones. Si un evento tiene una probabilidad de éxito p, ¿cuántos intentos debo realizar para al menos tener un éxito con probabilidad q? La respuesta es:
| t ≥ | log(1-q) |
| log(1-p) |
Se trata de obtener la variable t a partir de la fórmula q = 1-(1-p)t que podemos poner como 1-q = (1-p)t y aplicando logaritmos log(1-q) = t log(1-p) finalmente obtenemos t = log(1-q) / log(1-p) teniendo en cuenta que para garantizar q entonces t puede ser igual o mayor que ese valor.
Para garantizar una probabilidad de éxito de un 93.5% de que obtengamos al menos un vez el evento con probabilidad 1/6 necesitamos ejecutar 15 pruebas como vimos antes y también nos dice esta fórmula:
| t ≥ | log(1-0.935) | ≥ 14.992 |
| log(1-1/6) |
Hemos aplicado estos cálculos partiendo de un grafo del que conocemos todos los cortes. Pero al algoritmo debe trabajar sin ese conocimiento previo. En un grafo con n nodos hay como máximo 2n-1-1 cortes, entre los cuales hay como máximo C(n, 2) cortes mínimos. Decimos "como máximo" pues en el ejemplo del grafo con 4 nodos habían 2 cortes mínimos que superan C(4, 2) = 6, valor que es el que como máximo podemos encontrar por ejemplo en un grafo cíclico con 4 nodos, pues hay exactamente 6 cortes mínimos posibles y es el máximo de cortes mínimos que pueden darse en cualquier grafo. Puede ver como se llega a esa conclusión en la página de Wikipedia.
Entonces la probabilidad de éxito de que uno de los cortes sea mínimo es 1/C(n,2) y la de fracaso es 1-1/C(n,2).
Si hacemos t pruebas y queremos garantizar una probalidad de éxito q = 1-1/n de obtener al menos un corte mínimo, con lo que la probabilidad de fracaso es 1/n entonces para una probabilidad p de que un evento tenga éxito la de fracaso será 1-p, deduciendose lo siguiente:
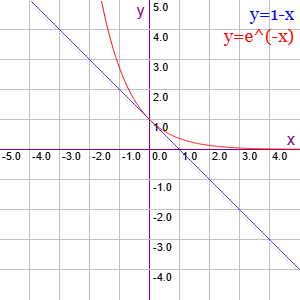
En lo anterior aplicamos la desigualdad 1-p ≤ e-p puesto que la gráfica de la función y = 1-x está siempre por debajo o es igual a la función y = e-x, como vemos en la Figura.
Si p = 1/C(n,2) entonces hemos de hacer las siguientes o más repeticiones para asegurar una probabilidad de éxito 1-1/n de obtener al menos un corte mínimo:
t ≥ C(n, 2) log(n)Y esto es lo que aplicamos en el algoritmo Karger con algunas consideraciones que veremos a continuación.
edita-funcion: y=1-x; # y=exp(-x) _anchoxy: 300 _altoxy: 300 _zoomx: 30 _zoomy: 30 _titulo-grafica: y=1-x y=e^(-x) _colores-titulo-grafica: blue,red
Si n = 10 entonces la probabilidad de éxito es 1-1/n = 1-1/10 = 0.9, con lo que para grafos con 10 o más nodos el algoritmo garantiza una probabilidad de éxito igual o superior al 90% si imponemos un número de repeticiones igual o superior a C(n,2) log(n).
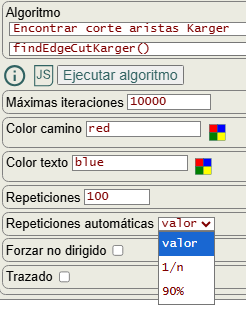
Como se observa en la Figura, con la opción repeticiones automáticas establecida a "valor (value)" la aplicación usará el valor que especifiquemos en la opción repeticiones, 100 que viene por defecto y que hemos usado en el ejemplo visto con 4 nodos que se obtenía una probabilidad practicamente del 100%.
Con "1/n" en repeticiones automáticas se usará la fórmula que vimos antes t = C(n, 2) log(n) siendo la probabilidad de éxito de 1-1/n Esto para un grafo con n=4 nodos como el que hemos estado viendo suponen t = C(4, 2) log(4) ≈ 8.32 que se redondea al entero superior 9, con lo que la probabilidad de éxito es 1-1/n = 1-1/4 = 0.75
Con la opción "90%" la aplicación calcula cuántas repeticiones necesitamos para garantizar el 90% con otra fórmula que ya vimos más arriba t = log(1-0.9) / log(1-p) que particularizando valores tenemos t = log(1-0.9) / log(1-1/C(n,2)) y por ejemplo para n=4 suponen log(1-0.9) / log(1-1/C(4,2)) ≈ 12.63 que redondeamos al entero superior 13.
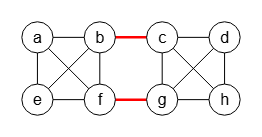
En la Figura vemos el corte mínimo de aristas en un grafo con 8 nodos obtenido con el algoritmo de Karger, obteniéndose los siguientes resultados según la opción repeticiones automáticas.
Encontrar corte aristas Karger: {
"edges":[[1,2],[5,6]],
"length":2,
"repetitions":100,
"successProbability":0.973662576832582,
"contractions":600}Con "valor (value)" en repeticiones automáticas se ejecutan 100 repeticiones con una probabilidad de éxito de ≈ 0.974 y se hacen 600 contracciones.
Encontrar corte aristas Karger: {
"edges":[[1,2],[5,6]],
"length":2,
"repetitions":59,
"successProbability":0.875,
"contractions":354}Con "1/n" en repeticiones automáticas sólo necesitamos repetir 59 veces con una probabilidad de 0.875 y 354 contracciones.
Encontrar corte aristas Karger: {
"edges":[[1,2],[5,6]],
"length":2,
"repetitions":64,
"successProbability":0.9,
"contractions":384}Con "90%" hemos de repetir 64 veces garantizándose la probabilidad de éxito de 0.9 con 384 contracciones. Puede importar ese ejemplo con este JSON:
{"nodes":[
{"index":0,"nodeOffset":"-35 2.5","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"6.67 -22.5","parent":[{"index":0}]},
{"index":2,"nodeOffset":"31.67 -47.5","parent":[{"index":1}]},
{"index":3,"nodeOffset":"56.67 -72.5","parent":[{"index":2}]},
{"index":4,"nodeOffset":"-51.67 2.5","parent":[{"index":0},{"index":1}]},
{"index":5,"nodeOffset":"-26.67 -22.5","parent":[{"index":4},{"index":1},{"index":0}]},
{"index":6,"nodeOffset":"-1.67 -47.5","parent":[{"index":5},{"index":2},{"index":3}]},
{"index":7,"nodeOffset":"40 -72.5","parent":[{"index":6},{"index":3},{"index":2}]}
],
"config":{
"nodeValueAuto":"alphabetic-lower",
"algorithm":"Find edge cut Karger",
"autoRepetitions":"90%"
}}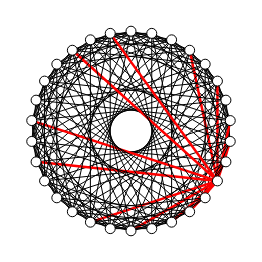
En la Figura vemos un grafo Circulante con 30 nodos y lista de índices 2,3,5,7,11,13 que tiene 180 aristas. Creo que hay 30 cortes mínimos de 12 aristas, teniendo muchos más cortes superiores como de 22, 30, 52, 62, 78, 84 o 94 aristas entre otros, números que se pueden comprobar en la aplicación ejecutando una única repetición y la opción "valor" para repeticiones automáticas y ver que cortes encuentra, pues la probabilidad será solo del 0.2% y devolverá cortes mínimos y no mínimos.
En los resultados siguientes ejecutamos el algoritmo de Karger con la opción "value" con 100 repeticiones con una probabilidad más bien baja de 20.56%, con 2800 contracciones y un tiempo de ejecución de 50 ms.
Con la opción "1/n" necesitamos 1480 repeticiones con probabilidad del 96.67%, con 41440 contracciones y con un tiempo de 670 ms. Con la opción "90%" necesitaremos menos repeticiones 1001, contracciones 28028 y tiempo 453 ms.
Opción "value"
Time: 50 ms
Encontrar corte aristas Karger: {
"edges":[[0,23],[10,23],[6,23],[12,23],[4,23],[18,23],[20,23],[21,23],[23,28],[23,25],[23,26],[16,23]],
"length":12,
"repetitions":100,
"successProbability":0.2055853293435086,
"contractions":2800}
-----------------------------------
Opción "1/n"
Time: 670 ms
Encontrar corte aristas Karger: {
"edges":[[0,17],[10,17],[15,17],[12,17],[4,17],[17,28],[17,20],[6,17],[14,17],[17,19],[17,24],[17,22]],
"length":12,
"repetitions":1480,
"successProbability":0.9666666666666667,
"contractions":41440}
-----------------------------------
Opción "90%"
Time: 453 ms
Encontrar corte aristas Karger: {
"edges":[[0,11],[11,22],[6,11],[11,28],[11,13],[11,18],[8,11],[11,24],[11,16],[9,11],[11,14],[4,11]],
"length":12,
"repetitions":1001,
"successProbability":0.9,
"contractions":28028}Como hemos comentado otras veces, se implementa en la aplicación un control de iteraciones para evitar que se colapse el navegador. Se establece por defecto en 10000 iteraciones. Así para las opciones "1/n" y "90%" anteriores necesitamos especificar 50000 iteraciones máximas, tal como vemos en el JSON siguiente que puede usar para importar ese ejemplo. Si el algoritmo se corta por llegar al máximo de iteraciones, devolverá los resultados alcanzados hasta ese momento con una frase de advertencia Máximas iteraciones 10000 alcanzadas
{"nodes":[
{"index":0,"nodeOffset":"19.17","parent":-1},
{"index":1,"nodeOffset":"-5.85 0.87","parent":-1},
{"index":2,"nodeOffset":"64.42 -21.54","parent":0},
{"index":3,"nodeOffset":"67.31 -17.36","parent":[0,1]},
{"index":4,"nodeOffset":"69.19 -11.77","parent":[1,2]},
{"index":5,"nodeOffset":"69.75 -5","parent":[0,2,3]},
{"index":6,"nodeOffset":"68.8 2.64","parent":[1,3,4]},
{"index":7,"nodeOffset":"66.19 10.82","parent":[0,2,4,5]},
{"index":8,"nodeOffset":"61.85 19.18","parent":[1,3,5,6]},
{"index":9,"nodeOffset":"76.25 2.36","parent":[2,4,6,7]},
{"index":10,"nodeOffset":"58.57 10","parent":[3,5,7,8]},
{"index":11,"nodeOffset":"47.45 41.77","parent":[0,4,6,8,9]},
{"index":12,"nodeOffset":"36.88 47.36","parent":[1,5,7,9,10]},
{"index":13,"nodeOffset":"25.29 51.54","parent":[0,2,6,8,10,11]},
{"index":14,"nodeOffset":"12.99 54.13","parent":[1,3,7,9,11,12]},
{"index":15,"nodeOffset":"9.64 30","parent":[2,4,8,10,12,13]},
{"index":16,"nodeOffset":"-12.96 29.13","parent":[3,5,9,11,13,14]},
{"index":17,"nodeOffset":"-15.94 51.54","parent":[0,4,6,10,12,14,15]},
{"index":18,"nodeOffset":"-27.53 47.36","parent":[1,5,7,11,13,15,16]},
{"index":19,"nodeOffset":"-38.1 41.77","parent":[0,2,6,8,12,14,16,17]},
{"index":20,"nodeOffset":"-47.36 35","parent":[1,3,7,9,13,15,17,18]},
{"index":21,"nodeOffset":"-56.97 2.36","parent":[2,4,8,10,14,16,18,19]},
{"index":22,"nodeOffset":"-72.99 -5.82","parent":[3,5,9,11,15,17,19,20]},
{"index":23,"nodeOffset":"-56.85 10.82","parent":[0,4,6,10,12,16,18,20,21]},
{"index":24,"nodeOffset":"-59.45 2.64","parent":[1,5,7,11,13,17,19,21,22]},
{"index":25,"nodeOffset":"-60.4 -5","parent":[0,2,6,8,12,14,18,20,22,23]},
{"index":26,"nodeOffset":"-59.84 -11.77","parent":[1,3,7,9,13,15,19,21,23,24]},
{"index":27,"nodeOffset":"-57.97 -17.36","parent":[0,2,4,8,10,14,16,20,22,24,25]},
{"index":28,"nodeOffset":"-55.07 -21.54","parent":[0,1,3,5,9,11,15,17,21,23,25,26]},
{"index":29,"nodeOffset":"-51.47 -24.13","parent":[1,2,4,6,10,12,16,18,22,24,26,27]}
],
"config":{
"nodeValueAuto":"none",
"nodeRadius":2,
"algorithm":"Find edge cut Karger",
"maxIter":50000,
"autoRepetitions":"1/n"
}}JavaScript del algoritmo Karger findEdgeCutKarger()
A continuación vemos el JavaScript del algoritmo findEdgeCutKarger():
function findEdgeCutKarger({matrix=[], forceUndirected="false", repetitions=100, autoRepetitions="none"}) {
let result = {edges: [], length: 0, repetitions, successProbability: 0, contractions: 0}, temp;
try {
let directed = isGraphDirected({matrix});
if (typeof directed==="string") throw new Error(directed);
if (directed) {
if (!forceUndirected) {
throw new Error(`The graph is directed and should be applied to undirected graphs or use the force undirected option`);
} else {
if (temp = operateDirectionGraph({matrix, edgesDirection:"undirected"}), temp.error) throw new Error(temp.error);
matrix = temp.matrix;
}
}
if (temp = isGraphConnected({matrix, forceUndirected:true}), typeof temp==="string") throw new Error(temp);
if (!temp) throw new Error(`The graph is not connected`);
if (temp = getMatrixModeValue({matrix}), typeof temp==="string") throw new Error(temp);
let [modeValue, nullValue] = temp;
let n = matrix.length;
let matrixCopy = JSON.parse(JSON.stringify(matrix));
for (let i=0; i<n; i++) {
matrixCopy[i][i] = null;
for (let j=i+1; j<n; j++) {
if (matrixCopy[i][j]!==nullValue) {
matrixCopy[i][j] = `(${i};${j})`;
matrixCopy[j][i] = matrixCopy[i][j];
} else {
matrixCopy[i][j] = null;
matrixCopy[j][i] = null;
}
}
}
let matrixReserve = JSON.parse(JSON.stringify(matrixCopy));
let cn = (n**2-n)/2;
if (autoRepetitions==="value") {
result.successProbability = 1-(1-1/cn)**repetitions;
} else if (autoRepetitions==="1/n") {
repetitions = Math.ceil(cn * Math.log(n));
result.repetitions = repetitions;
result.successProbability = 1-(1/n);
} else {
repetitions = Math.ceil(Math.log(1-0.9) / Math.log(1-1/cn));
result.repetitions = repetitions;
result.successProbability = 0.9;
}
for (let r=1; r<=repetitions; r++) {
let traceStep = [];
while (n = matrixCopy.length, n>2) {
result.contractions++;
if (temp = getEdges({matrix:matrixCopy, edgesCompact:true, modeValue:"null/value"}), typeof temp==="string") throw new Error(temp);
let edges = temp;
let min = 0, max = edges.length;
let k = Math.floor(Math.random() * (max - min) + min);
let [s, t] = edges[k];
if (temp = operateContractionGraph({matrix:matrixCopy, indexes:[s,t], typeMergedValue:"sum", omitSelfLoops:true}), temp.error) throw new Error("(operateContractionGraph) " + temp.error);
matrixCopy = temp.matrix;
}
let j = matrixCopy[0].findIndex(v => v!==null);
if (j>-1) {
let str = "[" + matrixCopy[0][j].replace(/\)\(/g, "],[").replace(/\(/, "[").replace(/\)/, "]").replace(/;/g, ",") + "]";
let edges = JSON.parse(str);
if (result.edges.length===0 || edges.length < result.edges.length) {
result.edges = edges;
result.length = edges.length;
}
}
matrixCopy = JSON.parse(JSON.stringify(matrixReserve));
}
} catch(e) {result = e.message}
return result;
}Esquemáticamente el algoritmo hace lo siguiente:
resultado = []
Repetir un número de repeticiones que asegure cierta probabilidad de éxito
Reponer con un copia del grafo inicial
Mientras el grafo tenga más de 2 nodos
Seleccionar una arista del grafo
Contraer el grafo
Fin mientras
Guardar la lista aristas del grafo si tiene menos elementos que la del resultado
Fin repetir
Devolver resultadoLa primera parte hasta la línea con let matrixReserve = ... comprueba que el grafo es no dirigido con isGraphDirected(), forzándolo a no dirigido si el argumento forceUndirected es verdadero con operateDirectionGraph(). A contiuación comprobamos si el grafo es conectado con isGraphConnected() pues el algoritmo sólo puede aplicarse a grafos conectados.
Obtenemos el modo valores de la matriz de entrada con getMatrixModeValue() que puede ser "0/1", "0/number", "null/value" o "false/true". Hacemos una copia de la matriz de entrada en matrixCopy y cambiamos todos los valores de las aristas con el texto "(u;v)" tal como ya explicamos. Finalmente hacemos otra copia de esa copia en matrixReserve para reponer en cada repetición.
Ahora empieza el verdadero algoritmo de Karger, calculando las repeticiones según el argumento autoRepetitions con las fórmulas que ya vimos. El bucle for (let r=1; r<=repetitions; r++) ejecuta esas repiticiones, con un bucle while (n = matrixCopy.length, n>2) interior que obtiene las aristas con getEdges(), selecciona aleatoriamente una de esas aristas y la contrae, hasta que el grafo sólo tenga dos nodos. Al salir de ese bucle interior guarda el corte si es de menor longitud que el almacenado previamente, volviendo a reponer la matriz copia inicial y ejecutando otra repetición.
Encontrar corte mínimo aristas Karger-Stein findEdgeCutKargerStein()

El algoritmo de Karger-Stein consigue una mejora con respecto al de Karger que vimos antes. Se basa en que la probabilidad de que se seleccione una arista de corte mínimo en la contracción aumenta al final, llegando a una probabilidad del 50% cuando el grafo alcanza un número determinado de nodos.
El algoritmo contrae aristas aleatorias en dos instancias del grafo hasta llegar a ⌈1+n/√2⌉ nodos, momento en el que hacemos dos llamadas recursivas con cada uno de los dos grafos contraídos hasta que tengamos un grafo con 6 o menos nodos, tras lo cual se aplican contracciones hasta el final con dos nodos, devolviéndose en el recursivo el resultado con menor corte de las dos llamadas.
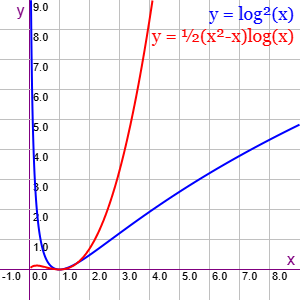
Para conseguir una probabilidad de éxito de 1-1/n hay que hacer log2(n) repeticiones, que son menos que la del algoritmo de Karger C(n, 2) log(n) cuya diferencia se observa en la gráfica Figura, recordando que C(n, 2) = (n2-n)/2
En correspondencia con la gráfica, Karger-Stein es más eficiente en comparación con Karger cuanto más nodos tenga el grafo.
edita-funcion: y = (log(x))**2; # y = ((x**2-x)/2) * log(x); _anchoxy: 300 _altoxy: 300 _zoomx: 30 _zoomy: 30 _movex: -4 _movey: -4 _titulo-grafica: y = log²(x) y = ½(x²-x)log(x) _colores-titulo-grafica: blue, red _contorno: 1
En la Figura vemos el mismo grafo Circulante con 30 nodos que ya expusimos en un apartado anterior, donde con la opción "1/n" se ejecutaba con 41440 contracciones en 670 ms con el algoritmo de Karger y con una probabilidad de éxito de 0.967, mientras que ahora con Karger-Stein para esa misma probabilidad sólo necesita 19800 contracciones y 6132 llamadas recursivas con un tiempo de ejecución de 189 ms.
Time: 189 ms
Encontrar corte aristas Karger-Stein: {
"edges":[[0,13],[11,13],[13,18],[13,15],[6,13],[2,13],[8,13],[13,24],[13,26],[13,16],[13,20],[10,13]],
"length":12,
"repetitions":12,
"successProbability":0.9666666666666667,
"contractions":19800,
"recursions":6132}
{"nodes":[
{"index":0,"nodeOffset":"19.17","parent":-1},
{"index":1,"nodeOffset":"-5.85 0.87","parent":-1},
{"index":2,"nodeOffset":"64.42 -21.54","parent":0},
{"index":3,"nodeOffset":"67.31 -17.36","parent":[0,1]},
{"index":4,"nodeOffset":"69.19 -11.77","parent":[1,2]},
{"index":5,"nodeOffset":"69.75 -5","parent":[0,2,3]},
{"index":6,"nodeOffset":"68.8 2.64","parent":[1,3,4]},
{"index":7,"nodeOffset":"66.19 10.82","parent":[0,2,4,5]},
{"index":8,"nodeOffset":"61.85 19.18","parent":[1,3,5,6]},
{"index":9,"nodeOffset":"76.25 2.36","parent":[2,4,6,7]},
{"index":10,"nodeOffset":"58.57 10","parent":[3,5,7,8]},
{"index":11,"nodeOffset":"47.45 41.77","parent":[0,4,6,8,9]},
{"index":12,"nodeOffset":"36.88 47.36","parent":[1,5,7,9,10]},
{"index":13,"nodeOffset":"25.29 51.54","parent":[0,2,6,8,10,11]},
{"index":14,"nodeOffset":"12.99 54.13","parent":[1,3,7,9,11,12]},
{"index":15,"nodeOffset":"9.64 30","parent":[2,4,8,10,12,13]},
{"index":16,"nodeOffset":"-12.96 29.13","parent":[3,5,9,11,13,14]},
{"index":17,"nodeOffset":"-15.94 51.54","parent":[0,4,6,10,12,14,15]},
{"index":18,"nodeOffset":"-27.53 47.36","parent":[1,5,7,11,13,15,16]},
{"index":19,"nodeOffset":"-38.1 41.77","parent":[0,2,6,8,12,14,16,17]},
{"index":20,"nodeOffset":"-47.36 35","parent":[1,3,7,9,13,15,17,18]},
{"index":21,"nodeOffset":"-56.97 2.36","parent":[2,4,8,10,14,16,18,19]},
{"index":22,"nodeOffset":"-72.99 -5.82","parent":[3,5,9,11,15,17,19,20]},
{"index":23,"nodeOffset":"-56.85 10.82","parent":[0,4,6,10,12,16,18,20,21]},
{"index":24,"nodeOffset":"-59.45 2.64","parent":[1,5,7,11,13,17,19,21,22]},
{"index":25,"nodeOffset":"-60.4 -5","parent":[0,2,6,8,12,14,18,20,22,23]},
{"index":26,"nodeOffset":"-59.84 -11.77","parent":[1,3,7,9,13,15,19,21,23,24]},
{"index":27,"nodeOffset":"-57.97 -17.36","parent":[0,2,4,8,10,14,16,20,22,24,25]},
{"index":28,"nodeOffset":"-55.07 -21.54","parent":[0,1,3,5,9,11,15,17,21,23,25,26]},
{"index":29,"nodeOffset":"-51.47 -24.13","parent":[1,2,4,6,10,12,16,18,22,24,26,27]}
],
"config":{
"nodeValueAuto":"none",
"nodeRadius":2,
"algorithm":"Find edge cut Karger-Stein",
"maxIter":50000
}}Si no cambiamos el máximo iteraciones y lo dejamos en 10000 tal como viene por defecto, la aplicación ejecuta y devuelve los resultados alcanzados hasta ese momento, advirtiendo con un mensaje Maximum iterations 10000 reached
por lo que el resultado no debe considerarse correcto si el algoritmo no pudo finalizar. En la Figura siguiente vemos el mensaje de error, con un resultado aparentemente correcto pero habiendo realizado solo 2362 recursiones de un total de 6132 y 7638 contracciones de un total de 19800.
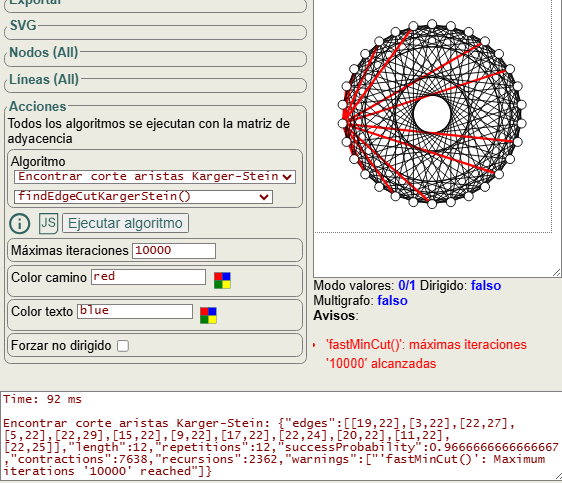
Los algoritmos de Karger y Karger-Stein se aplican sólo a grafos no dirigidos y no ponderados. En la aplicación podemos forzar no dirigido como también vemos en la Figura.
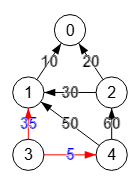
Forzando a no dirigido el grafo de la Figura encuentra un corte mínimo [[1,3],[3,4]], pudiendo también obtenerse el otro corte mínimo [[1,0],[2,0]] igualmente válido. Se ignoran las direcciones y los pesos de las aristas. Con otro algoritmo como findEdgeCutGomoryHu() que también se aplica a no dirigidos pero se puede forzar a ello, sin embargo sí tiene en cuenta los pesos, obteniéndose sólo el corte [[1,0],[2,0]] pues tiene una suma de pesos 10+20=30 inferior a 35+5=40 del otro corte [[1,3],[3,4]].
Encontrar corte aristas Karger-Stein: {
"edges":[[1,3],[3,4]],
"length":2,
"repetitions":22,
"successProbability":0.9,
"contractions":66,
"recursions":0}
{"nodes":[
{"index":0,"parent":[{"index":-1}]},
{"index":1,"parent":[{"index":0,"value":10}]},
{"index":2,"parent":[{"index":0,"value":20},{"index":1,"value":30}]},
{"index":3,"parent":[{"index":1,"value":35},{"index":4,"value":5}]},
{"index":4,"parent":[{"index":1,"value":50},{"index":2,"value":60}]}
],
"config":{
"markerEnd":"arrow",
"algorithm":"Find edge cut Karger-Stein",
"forceUndirected":true
}}Este es el JavaScript del algoritmo findEdgeCutKargerStein():
function findEdgeCutKargerStein({matrix=[], forceUndirected="false"}){
let result = {edges: [], length: 0, repetitions: 0, successProbability: 0, contractions: 0, recursions: 0}, temp;
try {
let directed = isGraphDirected({matrix});
if (typeof directed==="string") throw new Error(directed);
if (directed) {
if (!forceUndirected) {
throw new Error(`The graph is directed and should be applied to undirected graphs or use the force undirected option`);
} else {
if (temp = operateDirectionGraph({matrix, edgesDirection:"undirected"}), temp.error) throw new Error(temp.error);
matrix = temp.matrix;
}
}
if (temp = isGraphConnected({matrix, forceUndirected:true}), typeof temp==="string") throw new Error(temp);
if (!temp) throw new Error(`The graph is not connected`);
if (temp = getMatrixModeValue({matrix}), typeof temp==="string") throw new Error(temp);
let [modeValue, nullValue] = temp;
let n = matrix.length;
let matrixCopy = JSON.parse(JSON.stringify(matrix));
for (let i=0; i<n; i++) {
matrixCopy[i][i] = null;
for (let j=i+1; j<n; j++) {
if (matrixCopy[i][j]!==nullValue) {
matrixCopy[i][j] = `(${i};${j})`;
matrixCopy[j][i] = matrixCopy[i][j];
} else {
matrixCopy[i][j] = null;
matrixCopy[j][i] = null;
}
}
}
function getEdgesCut(matrixContracted){
let str = "[" + matrixContracted[0][1].replace(/\)\(/g, "],[").replace(/\(/, "[").replace(/\)/, "]").replace(/;/g, ",") + "]";
return JSON.parse(str);
}
function contract({matrix=[], t=0}) {
let matrixCopy = JSON.parse(JSON.stringify(matrix));
let n;
while (n = matrixCopy.length, n>t) {
result.contractions++;
if (temp = getEdges({matrix:matrixCopy, edgesCompact:true, modeValue:"null/value"}), typeof temp==="string") throw new Error(temp);
let edges = temp;
let min = 0, max = edges.length;
let k = Math.floor(Math.random() * (max - min) + min);
let [s, t] = edges[k];
if (temp = operateContractionGraph({matrix:matrixCopy, indexes:[s,t], typeMergedValue:"sum", omitSelfLoops:true}), temp.error) throw new Error("(operateContractionGraph) " + temp.error);
matrixCopy = temp.matrix;
}
return matrixCopy;
}
function fastMinCut({matrix=[]}) {
result.recursions++;
let n = matrix.length;
if (n<=6) {
let m = contract({matrix, t:2});
return getEdgesCut(m);
} else {
let t = Math.ceil(1 + n / Math.SQRT2);
let ma = contract({matrix, t});
let mb = contract({matrix, t});
let a = fastMinCut({matrix:ma});
let b = fastMinCut({matrix:mb});
return a.length<b.length ? a : b;
}
}
result.repetitions = n>9 ? Math.ceil((Math.log(n))**2) : Math.ceil(Math.log(1-0.9) / Math.log(1-2/(n**2-n)));
result.successProbability = n>9 ? 1-1/n : 0.9;
for (let i=1; i<=result.repetitions; i++) {
let edges;
if (n>9) {
edges = fastMinCut({matrix: matrixCopy});
} else {
let m = contract({matrix: matrixCopy, t:2});
edges = getEdgesCut(m);
}
if (result.edges.length===0 || edges.length<result.edges.length) {
result.edges = edges;
result.length = edges.length;
}
}
} catch(e) {result = e.message}
return result;
}De forma esquemática el algoritmo hace lo siguiente:
Función Contraer(grafo, t)
Mientras el grafo tenga mas de t nodos
Seleccionar una arista del grafo
Contraer el grafo
Fin mientras
Devolver el grafo con t nodos
Fin función
Función Recursivo(grafo)
Si el grafo tiene 6 o menos nodos
Contraer(grafo, 2)
devolver etiqueta única arista
En otro caso
Calcular t = 1 + n / sqrt(2)
grafo A = Contraer(grafo, t)
grafo B = Contraer(grafo, t)
lista aristas A = Recursivo(grafo A)
lista aristas B = Recursivo(grafo B)
Devolver la lista A o B con menos aristas en el corte
Fin si
Fin función
resultado = []
Repetir un número de repeticiones que asegure cierta probabilidad de éxito
Si el grafo tiene 10 o más nodos
aristas corte = Recursivo(grafo)
En otro caso
aristas corte = Contraer(grafo, 2)
Fin si
Si aristas corte es menor guardar en resultado
Fin repetir
Devolver resultadoLa primera parte hasta function getEdgesCut() prepara la matriz de entrada para el algoritmo, tal como explicamos en el código del anterior algoritmo Karger. Entonces se declaran intermante tres funciones:
getEdgesCut(matrixContracted)que convierte en Array la única arista del grafo contraído hasta dos nodos, arista que tiene un formato de cadena de texto (String) como"(1;2)(5;6)"y hay que convertirlo en Arrays de JavaScript[[1,2],[5,6]].contract({matrix=[], t=0})que contrae la matriz hasta que queden "t" nodos.fastMinCut({matrix=[]})recursivo que aplica t = ⌈1+n/√2⌉ y contrae dos ejemplares de la matriz, llamando recursivamente a cada matriz contraída hasta el caso basen<=6, momento en que contrae hasta que queden dos nodos. A la vuelta de las dos llamadas devolverá el menor de los dos cortes.
El algoritmo se ejecuta con el último bucle for con unas repeticiones que se calculan según el número de nodos del grafo. Si tiene menos de 10 nodos calculamos cuántas repeticiones necesitamos para contraer aleatoriamente aristas y obtener un corte mínimo con probabilidad mayor o igual que el 90%, lo mismo que hacíamos con el algoritmo de Karger. Entonces en cada repetición llamamos a la función interna contract({matrix: matrixCopy, t:2}) de donde se obtiene el corte mínimo, que es equivalente al algoritmo de Karger con la opción repeticiones automáticas "90%".
Para grafos con 10 o más nodos el número de repeticiones es r = log2(n) y entonces llamamos a fastMinCut({matrix: matrixCopy}) que aplica el verdadero algoritmo de Karger-Stein.