Acciones 2 sobre grafos
Introducción
En el tema que explicamos la estructura JSON que usa la aplicación Grafos SVG vimos como importar y exportar entre JSON y otras estructuras como matriz de adyacencia, lista de aristas, lista de adyacencias, matriz de incidencia y matriz de distancias. En esa gestión interviene la estructura JSON.
Alternativamente implementamos algoritmos para convertir entre la matriz de adyacencia y esas otras estructuras, sin intervenir el JSON:
convertToAdjacencyMatrix({array=[], mode="edgeList"})para convertir a matriz de adyacencia una lista de aristas, lista de adyacencias, matriz de incidencia o matriz de distancias que se pasa en el argumentoarray.getEdges({matrix})para obtener lista aristas desde la matriz de adyacencia pasada enmatrix.getAdjacencies({matrix})para obtener lista adyacencias desde la matriz de adyacencia pasada enmatrix.getIncidences({matrix})para obtener matriz incidencias desde la matriz de adyacencia pasada enmatrix.getDistances({matrix})para obtener matriz de distancias desde la matriz de adyacencia pasada enmatrix.
Ya tenía implementado convertToAdjacencyMatrix() y getEdges(), ahora implemento el resto y las agrupo todas en la sección de algorimtos.
Convertir a matriz de adyacencia convertToAdjacencyMatrix()
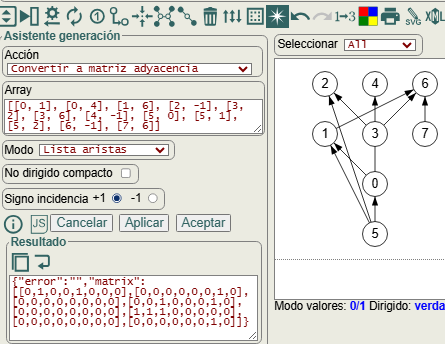
En la aplicación tenemos el algoritmo convertToAdjacencyMatrix() que recibe una lista de aristas (edgeList), lista de adyacencia (adjacencyList), matriz de incidencia (incidenceMatrix) o matriz de distancias (distanceMatrix) y la convierte en una matriz de adyacencia, actualizando el grafo en la aplicación. Esto quiere decir que puede usarse también para importar en la aplicación un grafo con esas estructuras de entrada.
En el tema de estructuras de datos ya las habíamos explicado en relación con la estructura JSON que es la que usa la aplicación, mientras que aquí se gestionan en relación con la matriz de adyacencia.
Vemos en este ejemplo el área de texto Array que es para incluir alguno de los datos de entrada como lista aristas, lista adyacencia, matriz incidencia o matriz distancias, modo que hemos de seleccionar. La opción no dirigido compacto es sólo para lista de aristas, apareciendo desmarcado en este caso pues el ejemplo es de un grafo dirigido. La opción signo incidencia es sólo para matriz incidencia.
Lista aristas: [[0, 1], [0, 4], [1, 6], [2, -1], [3, 2], [3, 6], [4, -1], [5, 0], [5, 1], [5, 2], [6, -1], [7, 6]] Matriz obtenida: [[0,1,0,0,1,0,0,0], [0,0,0,0,0,0,1,0], [0,0,0,0,0,0,0,0], [0,0,1,0,0,0,1,0], [0,0,0,0,0,0,0,0], [1,1,1,0,0,0,0,0], [0,0,0,0,0,0,0,0], [0,0,0,0,0,0,1,0]]
Usando esta lista de aristas vemos el resultado en la Figura que se actualiza en la aplicación a partir de la matriz de adyacencia obtenida.
A continuación se expone el JavaScript de esta función convertToAdjacencyMatrix().
function convertToAdjacencyMatrix({array=[], mode="edgeList", compactUndirected=false, signIncidence=1}) {
let result = [], temp;
try {
if (mode==="edgeList") {
if (array.some(v => !Array.isArray(v) || v.length<2 || v.length>3)) throw new Error(`Some array does not have correct length`);
let vertexs = [...new Set(array.map(v => [v[0], v[1]]).flat())].toSorted((v,w) => v-w).filter(v => v>-1).map(v => +v);
let n = vertexs[vertexs.length-1]+1;
let rest = vertexs.filter((v,i) => v!==i);
for (let r of rest) {
array.push([r, -1]);
}
let vertexsNum = vertexs.filter(v => v>-1);
if (![0,1].includes(vertexsNum[0])) throw new Error(`The first vertex is not 0 or 1`);
if (vertexs[0]===1) {
for (let i=0; i<array.length; i++) {
for (let j=0; j<array.length; j++) {
if (array[i][j]>0) array[i][j]--;
}
}
}
let [nullValue, valValue] = [0, 1];
for (let item of array) {
if (item.length===3) {
if (typeof item[2]==="string"){
[nullValue, valValue] = [null, ""];
break;
}
}
}
result = Array.from({length:n}, () => Array.from({length:n}, () => nullValue));
for (let k=0; k<array.length; k++) {
let [i, j, w] = array[k];
if (j>-1) {
let val = typeof w==="undefined" ? valValue : w;
result[i][j] = val;
if (compactUndirected) {
result[j][i] = val;
}
}
}
} else if (mode==="adjacencyList") {
let n = array.length;
let arr = [];
let m = -1;
array = array.map(v => v.length===0 ? [-1] : v);
for (let adj of array) {
for (let index of adj) {
let num = Array.isArray(index) ? index[0] : index;
if (num>m) m = num;
}
}
m++;
if (m!==n) throw new Error(`The array does not have the expected length (${m})`);
let [nullValue, valValue] = [0, 1];
for (let adj of array) {
for (let index of adj) {
if (Array.isArray(index) && typeof index[1]==="string") {
[nullValue, valValue] = [null, ""];
break;
}
}
}
result = Array.from({length: m}, () => Array.from({length: m}, () => nullValue));
for (let i=0; i<n; i++) {
for (let k=0; k<array[i].length; k++) {
let val = array[i][k];
let [j, w] = Array.isArray(val) ? val : [val];
if (j>-1) result[i][j] = typeof w==="undefined" ? valValue : w;
}
}
} else if (mode==="incidenceMatrix") {
let n = array.length;
let m = array[0].length;
let directed = array.flat().some(v => v===-1);
let edges = [];
for (let j=0; j<m; j++){
let edge = directed ? [-1, -1] : [];
for (let i=0; i<n; i++) {
if (directed) {
if (array[i][j]===-1*signIncidence) {
edge[1] = i;
} else if (array[i][j]===1*signIncidence) {
edge[0] = i;
} else if (array[i][j]===2*signIncidence) {
edge = [i, i];
} else if (array[i][j]===-2*signIncidence) {
edge = [i, i];
}
if (edge[0]>-1 && edge[1]>-1) break;
} else if (array[i][j]!==0) {
edge.push(i);
if (array[i][j]===2) edge.push(i);
if (edge.length===2) break;
}
}
edges.push(edge);
}
temp = convertToAdjacencyMatrix({array:edges, mode:"edgeList", compactUndirected:!directed});
if (typeof temp==="string") throw new Error(temp);
result = temp;
} else if (mode==="distanceMatrix") {
let n = array.length;
result = Array.from({length:n}, () => Array.from({length:n}, () => 0));
for (let i=0; i<n; i++) {
for (let j=0; j<n; j++) {
if (i!==j) {
let d = array[i][j];
result[i][j] = (d===Infinity || d==="∞") ? 0 : d===1 ? 1 : 0;
}
}
}
}
} catch(e) {result = e.message}
return result;
}Obtener lista aristas getEdges()
En la seccion de acciones podemos encontrar el algoritmo getEdges() para obtener las aristas de un grafo desde su matriz de adyacencia. En la Figura se muestran los parámetros forzar no dirigido, aristas compactas y pesos que explicaremos a continuación. En el tema de estructuras explicamos la lista de aristas gestionada desde el JSON de la aplicación, mientras que aquí se gestiona con la matriz de adyacencia.
Para todos los algoritmos y otras partes de la aplicación he incluido el enlace con el icono que remite a temas en este sitio que explican cada parte, como a este mismo apartado.
El icono es el del mismo botón que antes tenía con la leyenda "Código", que ahora abre un panel emergente con el código JavaScript del algoritmo.
En la parte inferior se muestra el resultado al ejecutar el algoritmo, con el tiempo de ejecución y el propio resultado convertido en texto.
Veamos un ejemplo en ejecución para el grafo de la Figura.
0 7 9 0 0 14 0 0 10 15 0 0 0 0 0 11 0 2 0 0 0 0 0 0 0 0 0 6 0 0 0 0 0 0 9 0
Este grafo dirigido y ponderado se encuentra entre las muestras de la aplicación. También puede importarlo con esta matriz de adyacencia en formato SSV.
Time: 0 ms
Obtener aristas: {
"0,1":7, "0,2":9, "0,5":14,
"1,2":10, "1,3":15, "2,3":11,
"2,5":2, "4,3":6, "5,4":9}Al ejecutarlo sin activar forzar no dirigido y aristas compactas obtenemos el resultado adjunto. Devuelve un objeto cuyas claves son las aristas y sus valores el valor de cada arista. Así, por ejemplo, "0,1":7 se refiere a la arista "0🡒1" que tiene el valor "7".
Time: 0 ms
Obtener aristas: {
"0,1":7, "1,0":7, "0,2":9,
"2,0":9, "0,5":14, "5,0":14,
"1,2":10, "2,1":10, "1,3":15,
"3,1":15, "2,3":11, "3,2":11,
"2,5":2, "5,2":2, "4,3":6,
"3,4":6, "5,4":9, "4,5":9}Si activamos forzar no dirigido sobre un grafo dirigido, sin usar aristas compactas se replican las aristas, por ejemplo, tenemos "0,1":7, "1,0":7 que, para un no dirigido, viene a ser la arista "0-1" con valor "7".
[[0,1],[0,2],[0,5], [1,2],[1,3],[2,3], [2,5],[4,3],[5,4]]
En caso de activar aristas compactas obtenemos un array en lugar de un objeto. Así, por ejemplo, [0, 1] se refiere a la arista "0🡒1". En cualquier caso con [i, j] siempre entenderemos "i🡒j" en un grafo dirigido e "i-j" en uno no dirigido. Vea que con este parámetro activado perdemos el valor de la arista, que podemos entender como pesos si esa opción que vimos en la Figura no está marcada.
[[0,1,7],[0,2,9],[0,5,14], [1,2,10],[1,3,15],[2,3,11], [2,5,2],[4,3,6],[5,4,9]]
Si con aristas compactas marcamos pesos obtenemos cada arista con tres posiciones como [0,1,7] donde 0,1 son los nodos de la arista y 7 es su peso. Esta opción para incluir pesos no tiene ningún efecto si no se usa aristas compactas.
La aplicación permite exportar las distintas acciones a Wolfram Cloud, como explicamos en un tema anterior cuando exponíamos las estructuras de datos. Como se observa en la Figura, al ejecutar el ejemplo anterior obtenemos el código Wolfram y un enlace para ir a Wolfram Cloud, donde tiene que abrir su sesión y pegar ese código que vemos también a continuación. Hacemos un ajuste de tamaños de imagen y de vértices para que el resultado tenga un aspecto lo más similar posible al grafo de nuestra aplicación.
g = AdjacencyGraph[{{0,1,1,0,0,1},{0,0,1,1,0,0},{0,0,0,1,0,1},{0,0,0,0,0,0},{0,0,0,1,0,0},{0,0,0,0,1,0}},
ImageSize->250, VertexSize->{"Scaled", 0.13}, VertexLabels->{1->Placed[0,Center],
2->Placed[1,Center], 3->Placed[2,Center], 4->Placed[3,Center], 5->Placed[4,Center],
6->Placed[5,Center]}, VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold],
EdgeLabels->{(1->2)->7, (1->3)->9, (2->3)->10, (2->4)->15, (3->4)->11, (5->4)->6, (6->5)->9, (1->6)->14, (3->6)->2},
VertexStyle->White, DirectedEdges->True, EdgeStyle->{{Black,Thickness[0.005]}}]
EdgeList[g]
En la Figura vemos el resultado en Wolfram Cloud, presentando el grafo original que es estructuralmente igual que el de la Figura obtenido en nuestra aplicación.
Y también ofrece la lista de aristas {1🡒2, 1🡒3, 1🡒6, 2🡒3, 2🡒4, 3🡒4, 3🡒6, 5🡒4, 6🡒5} que es la misma que la que obtuvimos [[0, 1], [0, 2], [0, 5], [1, 2], [1, 3], [2, 3], [2, 5], [4, 3], [5, 4]] si tenemos en cuenta que en Wolfram los índices se inician en 1 y en nuestra aplicación en 0. Tenga en cuenta que los nodos están etiquetados desde 0 como en nuestra aplicación, pero en Wolfram se inician en 1.
En el texto anterior he usado la flecha "🡒" en lugar de la que usa Wolfram que es el UNICODE 0F3D5 "", tal como explica en \[DirectedEdge] para una arista dirigida, pues no es representable directamente en los navegadores dado que está en una sección de uso privado en Unicode.
Nuestra aplicación nunca utiliza internamente caracteres flecha para representar una arista, pues tal como hemos explicado, el array [1, 2] significa "1🡒2" en un grafo dirigido y "1-2" o "2-1" en un grafo no dirigido.
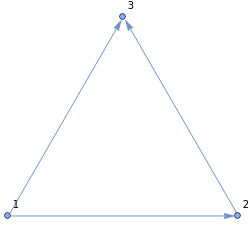
En el código de Wolfram puede escribirse la relación como a \[DirectedEdge] b o con DirectedEdge[a, b] o bien con a->b para dirigido, como por ejemplo Graph[{1\[DirectedEdge]2, DirectedEdge[1,3], 2->3}, VertexLabels->"Name"] que usando las tres formas creará el grafo dirigido que vemos en la Figura.
Y a \[UndirectedEdge] b o con DirectedEdge[a, b] o bien con a <-> b para no dirigido con el ejemplo Graph[{1\[UndirectedEdge]2, UndirectedEdge[1, 3], 2<->3}, VertexLabels->"Name"] que creará un grafo como el anterior pero sin flechas en las aristas para grafo no dirigido.
En el código siguiente de getEdges() usamos isGraphDirected() que ya vimos en un tema anterior. Y también getMatrixModeValue() para consultar el modo valores de la matriz de adyacencia.
function getEdges({matrix=[], forceUndirected=false, edgesCompact=false, weights=false}) {
let result = edgesCompact ? [] : {}, temp;
try {
let n = matrix.length;
if (temp = isGraphDirected({matrix}), typeof temp==="string") throw new Error(temp);
let directed = temp;
if (temp = getMatrixModeValue({matrix}), typeof temp==="string") throw new Error(temp);
let [modeValue, nullValue] = temp;
for (let i=0; i<n; i++) {
let k = (edgesCompact && !directed) ? i : 0;
for (let j=k; j<n; j++) {
if (matrix[i][j]!==nullValue) {
if (edgesCompact) {
let edge = [i, j];
if (weights) edge.push(matrix[i][j]);
result.push(edge);
} else {
result[`${i},${j}`] = matrix[i][j];
}
}
if (!edgesCompact) {
if (!directed) {
if (matrix[j][i]!==0) result[`${j},${i}`] = matrix[j][i];
} else if (forceUndirected && matrix[i][j]!==nullValue) {
result[`${j},${i}`] = matrix[i][j];
}
}
}
}
} catch(e) {result = e.message}
return result;
}El argumento edgesCompact se refiere al modo de aristas compactas que hemos explicado más arriba. Y también forceUndirected a forzar no dirigido.
Obtener lista adyacencias getAdjacencies()
En la Figura vemos las opciones para ejecutar el algoritmo obtener adyacencias que devuelve la lista de adyacencias a partir de una matriz de adyacencias. En el tema de estructuras explicamos la lista de adyacencia gestionada desde el JSON de la aplicación, mientras que aquí se gestiona con la matriz de adyacencia.
Obtener adyacencias: [[4],[0],[0,1],[0,1,4],[1,2]]
Con el grafo de la Figura y sin marcar la opción pesos que vemos en la Figura, obtenemos esta lista de adyacencias a cada nodo. Así por ejemplo el nodo "0" apunta al "4", es decir, la arista "0🡒4" se representa con la primera posición [4] en esa lista. El nodo "3" tiene tres aristas salientes "3🡒0", "3🡒1" y "3🡒4" que se representan con [0,1,4] en el índice 3 de la lista.
Obtener adyacencias: [
[[4,33]],
[[0,10]],
[[0,20],[1,30]],
[[0,44],[1,40],[4,11]],
[[1,50],[2,60]]
]Si marcamos la opción pesos, la lista agrega el peso. Así por ejemplo la arista "0🡒4" tiene un peso 33 con lo que queda indicado con [4,33] en la posición 0 de la lista. Con este JSON puede importar el ejemplo.
{"nodes":[
{"index":0,"nodeOffset":"-2","parent":[{"index":-1},{"index":4,"lineType":"quadratic","lineOffset":"8","value":33}]},
{"index":1,"nodeOffset":"-4.67","parent":[{"index":0,"value":10}]},
{"index":2,"nodeOffset":"0.67","parent":[{"index":0,"value":20},{"index":1,"value":30}]},
{"index":3,"nodeOffset":"-4.67","parent":[{"index":1,"value":40},{"index":4,"value":11},{"index":0,"lineType":"quadratic","lineOffset":-8,"value":44}]},
{"index":4,"nodeOffset":"0.67","parent":[{"index":1,"value":50},{"index":2,"value":60}]}
],
"config":{
"markerEnd":"arrow",
"algorithm":"Get adjacencies"
}}
Para el mismo grafo pero no dirigido de la Figura obtenemos esta lista de adyacencia sin marcar la opción pesos.
Obtener adyacencias: [[1,2,3,4],[0,2,3,4],[0,1,4], [0,1,4],[0,1,2,3]]
Obtener adyacencias: [
[[1,10],[2,20],[3,44],[4,33]],
[[0,10],[2,30],[3,40],[4,50]],
[[0,20],[1,30],[4,60]],
[[0,44],[1,40],[4,11]],
[[0,33],[1,50],[2,60],[3,11]]
]Marcando la opción pesos obtenemos esta lista de adyacencias. Con este JSON puede importar el ejemplo.
{"nodes":[
{"index":0,"nodeOffset":"-2 0","parent":[{"index":-1},{"index":4,"lineType":"quadratic","lineOffset":"8","value":33}]},
{"index":1,"nodeOffset":"-4.67 0","parent":[{"index":0,"value":10}]},
{"index":2,"parent":[{"index":0,"value":20},{"index":1,"value":30}]},
{"index":3,"nodeOffset":"-4.67 0","parent":[{"index":1,"value":40},{"index":4,"value":11},{"index":0,"lineType":"quadratic","lineOffset":-8,"value":44}]},
{"index":4,"nodeOffset":"0.67 0","parent":[{"index":1,"value":50},{"index":2,"value":60}]}
],
"config":{
"algorithm":"Get adjacencies"
}}Este es el JavaScript del algoritmo getAdjacencies() para obtener la lista de adyacencias desde un matriz de adyacencia. Usamos isGraphDirected() que ya vimos en un tema anterior. Y también getMatrixModeValue() para consultar el modo valores de la matriz de adyacencia.
function getAdjacencies({matrix=[], weights=false}) {
let result = [], temp;
try {
let n = matrix.length;
if (temp = isGraphDirected({matrix}), typeof temp==="string") throw new Error(temp);
let directed = temp;
if (temp = getMatrixModeValue({matrix}), typeof temp==="string") throw new Error(temp);
let [modeValue, nullValue] = temp;
result = Array.from({length:n}, () => []);
for (let i=0; i<matrix.length; i++){
let k = !directed ? i : 0;
for (let j=k; j<n; j++) {
let value = matrix[i][j];
if (value!==nullValue) {
let val = weights ? [j, value] : j;
result[i].push(val);
if (!directed){
val = weights ? [i, value] : i;
result[j].push(val);
}
}
}
}
} catch(e) {result = e.message}
return result;
}Obtener matriz incidencias getIncidences()
En la Figura vemos las opciones para ejecutar el algoritmo obtener incidencias que devuelve la matriz de incidencias a partir de una matriz de adyacencias. En el tema de estructuras explicamos la matriz de incidencias gestionada desde el JSON de la aplicación, mientras que aquí se gestiona con la matriz de adyacencia.
Con el grafo dirigido con autobucle y arista múltiple de la Figura obtenemos la lista de adyacencia siguiente. Explicamos este mismo ejemplo en el tema matriz de incidencias.
Obtener incidencias: [[-1,-1,0,0,0,0,0,0,0], [1,0,-1,0,-1,0,-1,0,0], [0,1,1,-2,0,0,0,-1,0], [0,0,0,0,1,1,0,0,-1], [0,0,0,0,0,-1,1,1,1]]
{"nodes":[
{"index":0,"parent":[{"index":-1}]},
{"index":1,"parent":[{"index":0}]},
{"index":2,"parent":[{"index":0},{"index":1},{"index":2,"lineType":"cubic","lineOffset":"4 4 4 -4"}]},
{"index":3,"parent":[{"index":1},{"index":4,"lineType":"quadratic","lineOffset":"0 4"}]},
{"index":4,"parent":[{"index":1},{"index":2},{"index":3}]}
],
"config":{
"markerEnd":"arrow",
"algorithm":"Get incidences"
}}Este es el JavaScript de getIncidences() para obtener la matriz de incidencias a partir de la matriz de adyacencia. Usamos isGraphDirected() que ya vimos en un tema anterior. Y también getMatrixModeValue() para consultar el modo valores de la matriz de adyacencia.
function getIncidences({matrix=[], signIncidence=1}) {
let result = [], temp;
try {
let n = matrix.length;
if (temp = isGraphDirected({matrix}), typeof temp==="string") throw new Error(temp);
let directed = temp;
if (temp = getEdges({matrix, edgesCompact:true}), typeof temp==="string") throw new Error(temp);
let edges = temp.filter(v => v[1]>-1);
let m = edges.length;
result = Array.from({length: n}, () => Array.from({length: m}, () => 0));
for (let k=0; k<edges.length; k++) {
let [i, j] = edges[k];
if (i===j) {
result[i][k] = (directed ? -1 : 1) * 2;
} else {
result[i][k] = signIncidence;
result[j][k] = (directed ? -1 : 1) * signIncidence;
}
}
} catch(e) {result = e.message}
return result;
}Obtener matriz de distancias getDistances()
En la Figura vemos las opciones para ejecutar el algoritmo obtener distancias que devuelve la matriz de distancias a partir de una matriz de adyacencias. En el tema de estructuras explicamos la matriz de distancias gestionada desde el JSON de la aplicación, mientras que aquí se gestiona con la matriz de adyacencia.
Vemos las opciones pesos, distancias infinito y método mínima distancia que también explicamos en ese tema matriz de distancias.
En la Figura vemos un grafo dirigido con arista múltiple y autobucle del que obtenemos esta matriz de distancias con la opción pesos sin marcar.
Obtener distancias: [[0, ∞, ∞, ∞, ∞], [1, 0, ∞, 1, ∞], [1, 1, 0, 2, ∞], [2, 1, ∞, 0, ∞], [2, 1, 1, 2, 1]]
Obtener distancias: [[0, Infinity, Infinity, Infinity, Infinity], [1, 0, Infinity, 1, Infinity], [1, 1, 0, 2, Infinity], [2, 1, Infinity, 0, Infinity], [2, 1, 1, 2, 1]]
Usando Infinity en la opción distancias infinito, en lugar de presentarlo con ∞ se usa el número Infinity de JavaScript.
Obtener distancias: [[0, ∞, ∞, ∞, ∞], [10, 0, ∞, 37, ∞], [20, 30, 0, 67, ∞], [24, 14, ∞, 0, ∞], [60, 50, 60, 87, 22]]
Marcando la opción pesos obtenemos esta matriz de distancias. Usa el método mínima distancia "dijkstra" por defecto. Ver más sobre esto en el tema matriz de distancias.
{"nodes":[
{"index":0,"nodeOffset":"10","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"-9.34","parent":[{"index":0,"value":10},{"index":3,"lineType":"quadratic","lineOffset":"2","value":37}]},
{"index":2,"nodeOffset":"1.34","parent":[{"index":0,"value":20},{"index":1,"value":30}]},
{"index":3,"nodeOffset":"-37.34 50","parent":[{"index":1,"value":14,"lineType":"quadratic","lineOffset":-2}]},
{"index":4,"nodeOffset":"15.34","parent":[{"index":1,"value":50},{"index":2,"value":60},{"index":4,"lineType":"cubic","lineOffset":"4 4 4 -4","value":22}]}
],
"config":{
"wv":84,
"hv":82.22,
"width":210,
"height":205.54,
"adjust":false,
"wvIni":84,
"markerEnd":"arrow",
"algorithm":"Get distances"
}}Con este JavaScript ejecutamos getDistances() para obtener la matriz de distancias a partir de la matriz de adyacencia. Usamos isGraphDirected() que ya vimos en un tema anterior. Y también getMatrixModeValue() para consultar el modo valores de la matriz de adyacencia.
function getDistances({matrix=[], infinityDistances="∞", weights=false, methodMinimumDistance="dijkstra"}) {
let result = [], temp;
try {
let n = matrix.length;
if (temp = isGraphDirected({matrix}), typeof temp==="string") throw new Error(temp);
let directed = temp;
if (temp = getMatrixModeValue({matrix}), typeof temp==="string") throw new Error(temp);
let [modeValue, nullValue] = temp;
let matrixCopy = [];
for (let i=0; i<n; i++) {
let arr = [];
for (let j=0; j<n; j++) {
let v = matrix[i][j];
let val = v===nullValue ? 0 : (!weights || modeValue==="null/value" || modeValue==="false/true") ? 1 : v;
arr.push(val);
}
matrixCopy.push(arr);
}
let infy = infinityDistances==="Infinity" ? Infinity : "∞";
result = Array.from({length:n}, () => Array.from({length:n}, () => infy));
let method = null;
if (methodMinimumDistance==="dijkstra") {
method = getShortestPathDijkstra;
} else if (methodMinimumDistance==="floyd") {
method = getShortestPathFloyd;
} else {
throw new Error(`Method for minimum distance ${methodMinimumDistance} is wrong`);
}
for (let i=0; i<n; i++) {
for (let j=0; j<n; j++) {
if (i===j) {
result[i][j] = matrixCopy[i][j];
} else {
if (temp = method({matrix:matrixCopy, firstIndex:i, lastIndex:j}), temp.error) throw new Error(temp.error);
let d = temp.lengthPath;
if (d===Infinity && infinityDistances==="∞") d = "∞";
result[i][j] = d;
}
}
}
} catch(e) {result = e.message}
return result;
}