Algoritmos voraces en JavaScript: Mochila fraccionable
Algoritmos voraces
Los algoritmos voraces se utilizan para resolver problemas de optimización. Suelen considerar un conjunto de candidatos que se van analizando, tomando en cada iteración el que a corto plazo resulte más aceptable para conseguir la optimalidad que se espera del resultado final. Una vez seleccionado un candidato se incorpora al resultado, no reconsiderándose más adelante dicha decisión y permaneciendo en la solución hasta el final. Si por alguna razón no llegamos a un resultado óptimo no habrá forma de deshacer las acciones. En esto se diferencia de otros algoritmos como el vuelta atrás (backtracking) donde se analizan todas las posibilidades, lo que hace que sea un algoritmo mucho más costoso.
La clave de estos algoritmos voraces está en la función que selecciona el mejor candidato. Podríamos decir que el algoritmo va seleccionando de forma codiciosa al candidato óptimo en ese momento, despreocupándose del resultado final. De hecho en inglés se denomina este algoritmo como greedy algorithms, por lo que creo que la denominación algoritmos codiciosos define mejor su comportamiento. De todas formas seguiré hablando de algoritmos voraces por ser la que ampliamente se utiliza.
El hecho de que no se puedan deshacer las acciones significará que un voraz no puede resolver todos los problemas de optimización. En este tema veremos el problema de la mochila (Figura) donde podemos seleccionar un objeto completo o una fracción del mismo con el objetivo de llenar la mochila con el mayor valor posible. Si los objetos son fraccionables podremos resolverlo con un voraz. En otro caso no será posible, como veremos en un apartado al final de este tema.
Hay una estructura subyacente en todo algoritmo voraz que podría plantearse como sigue:
function voraz(conjunto){
let resultado = crear(conjunto);
while (!esSolucion(resultado) && !esVacio(conjunto)){
let candidato = seleccionar(conjunto);
if (esCompletable(resultado, candidato)) {
resultado = guardar(resultado, candidato);
}
}
return resultado;
}Siempre habrá un conjunto de valores sobre los que tenemos que iterar para buscar los candidatos que formaran parte del resultado. Ese conjunto de partida podría ser un array, por ejemplo. Iniciaremos el algoritmo creando un resultado que viene a ser una estructura donde pondremos el conjunto de los candidatos elegidos. Es importante entender que los que formen parte del resultado permanecerán ahí hasta el final, pues el algoritmo voraz no vuelve a reconsiderar los que se desechen. Entramos entonces en el bucle, que se repetirá mientras el resultado no sea una solución y aún queden elementos en el conjunto que considerar.
La ejecución para seleccionar un nuevo candidato es de especial importancia, pues aquí es donde hemos de aplicar lo necesario para conseguir que el resultado sea una solución óptima. Si tras comprobar que ese candidato hace que el resultado complete la solución, lo agregamos al resultado.
Seleccionar el mejor candidato en cada momento nos llevará a obtener la mejor solución de la función objetivo. Esta función no está presente en el código pero esta implícita en la función de selección. La función objetivo será, por ejemplo, llenar una mochila con objetos que maximicen el valor o devolver cambio con el menor número de monedas, ejemplos que veremos en este y siguientes temas.
Hay mucha documentación sobre los algoritmos voraces en Intenert. Pero yo estoy siguiendo principamente los contenidos del capítulo 6 del libro Fundamentos de Algoritmia de G.Brassard, P.Bratley.
El problema de la mochila fraccionable
El problema de la mochila fraccionable se plantea que tenemos una mochila que puede cargar un peso máximo P y que tenemos n objetos fraccionables con un peso pi y un valor vi cada uno. Se trata de cargar la mochila sin pasarnos del peso máximo y maximizando el valor total seleccionando un objeto de cada clase en fracciones 0 ≤ xi ≤ 1 donde xi ∈ ℝ, es decir, podemos no seleccionar un objeto, seleccionarlo o tomar una fracción. Formalmente podemos escribirlo como sigue:
Con pi>0, vi>0, 0 ≤ xi ≤ 1 hemos de maximizar V = ∑(i=1..n) xi vi tal que ∑(i=1..n) xi pi ≤ P
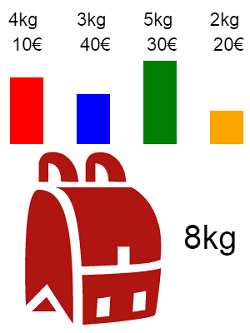
Supongamos que tenemos que llenar la mochila de la Figura con un peso máximo P de 8 kg para obtener el mayor valor posible V:
| Índice | Peso | Valor | Precio | Fracción |
|---|---|---|---|---|
| 0 | 4 | 10 | 2.5 | ? |
| 1 | 3 | 40 | 13.333 | ? |
| 2 | 5 | 30 | 6 | ? |
| 3 | 2 | 20 | 10 | ? |
Si tuviéramos que llenarla manualmente podríamos plantear tres estrategias, donde representamos un objeto como fracción × (N kg, M €):
- Seleccionar los objetos por orden de mayor valor ante la perspectiva de acumular objetos con más valor, con lo que la selección sería 1×(5kg, 30€) + 1×(3kg, 40€) = (8kg, 70€)
- Seleccionar los objetos por orden de menor peso ante la perspectiva de acumular una mayor cantidad de objetos, con lo que la selección sería 1×(2kg, 20€) + 1×(3kg, 40€) + 0.75×(4kg, 10€) = (8kg, 67.5€)
- Seleccionar los objetos por orden de mayor precio, considerando el dato valor/peso, con lo que la selección sería 1×(3kg, 40€, 13.333€/kg) + 1×(2kg, 20€, 10€/kg) + 0.6×(5kg, 30€, 6€/kg) = (8kg, 78€)
La estrategia del precio es la que consigue el mayor valor para este ejemplo, siendo la óptima para todos los casos. Vease que el precio máximo de la mochila es 78/8 = 9.75€/kg superior a las otras posibilidades. El precio final de un conjunto de objetos será máximo si vamos seleccionando objetos de mayor precio. En estos problemas habría que demostrar que la solución es óptima en todos los casos. Estas demostraciones no siempre son sencillas. En un apartado más abajo puede ver una forma de hacerlo.
Empezaremos aplicando el algoritmo teórico que vimos en el apartado anterior. Como datos de entrada tendremos el peso máximo que puede cargar la mochila, un array de pesos y otro de valores. Creamos una estructura que denominaremos conjunto que contendrá esos datos de entrada y un array indices que representan los índices de los objetos. Es en este array donde iremos seleccionando candidatos óptimos. Con las funciones accesorias aún sin definir y el voraz(conjunto) que vimos antes llegamos a un primer planteamiento estructural del problema:
function llenarMochilaTeorica(pesoMaximo=0, pesos=[], valores=[]){
let conjunto = {
pesoMaximo,
pesos,
valores,
indices: pesos.map((v,i) => i)
};
// Funciones accesorias (aún sin definir)
function crear(conjunto){}
function esSolucion(resultado){}
function esVacio(conjunto){}
function seleccionar(conjunto){}
function esCompletable(resultado, candidato){}
function guardar(resultado, candidato){}
// Algoritmo voraz
function voraz(conjunto){
let resultado = crear(conjunto);
while (!esSolucion(resultado) && !esVacio(conjunto)){
let candidato = seleccionar(conjunto);
if (esCompletable(resultado, candidato)) {
resultado = guardar(resultado, candidato);
}
}
return resultado;
}
return voraz(conjunto);
}Vamos ahora a definir las funciones accesorias. Con crear(conjunto) creamos una estructura de datos para almacenar el resultado. Contiene un array fracciones cuyos valores serán una fraccion [0, 1] de cada objeto, pesoMochila que va acumulando el peso de la mochila y una referencia a la estructura conjunto:
function crear(conjunto){
return {
fracciones: conjunto.pesos.map(v => 0),
pesoMochila: 0,
conjunto
};
}Sabremos si un resultado es solución comprobando que el peso de la mochila es exactamente el peso máximo a cargar. Vease que siempre alcanzaremos el peso máximo, pues cuando ya no quepa un siguiente objeto completo siempre podremos fraccionarlo hasta alcanzar el peso máximo:
function esSolucion(resultado){
return resultado.pesoMochila === resultado.conjunto.pesoMaximo;
}El conjunto de índices para un tamaño de n objetos será inicialmente el array [0, 1, 2,..., n-1]. Cuando seleccionemos un candidato eliminaremos el índice en ese array, por lo que sabremos que el conjunto está vacío cuando ese array esté vacío:
function esVacio(conjunto){
return conjunto.indices.length===0;
}La función más importante de un voraz es la que selecciona un candidato. Se trata en este caso de buscar el objeto cuyo precio, es decir, la la relación valor/peso, sea la mayor entre los objetos disponibles. Si vamos eligiendo el objeto de mayor precio tendremos una mochila con el mayor valor posible. Esta función recorre los índices del conjunto y selecciona el de mayor precio, tras lo cual elimina ese índice del array de índices:
function seleccionar(conjunto){
let precioMayor = 0;
let seleccionado = -1;
let j = -1;
for (let i=0; i<conjunto.indices.length; i++){
let index = conjunto.indices[i];
let precio = conjunto.valores[index] / conjunto.pesos[index];
if (precio > precioMayor){
precioMayor = precio;
seleccionado = index;
j = i;
}
}
conjunto.indices.splice(j, 1);
return seleccionado;
}Una vez seleccionado un candidato hemos de comprobar que completa la solución. Como hemos dicho antes, todo candidato puede completar el resultado dado que o tomamos un objeto completo o una fracción del mismo. Por lo tanto para este problema la función esCompletable() siempre devolverá verdadero:
function esCompletable(resultado, candidato){
return true;
}Por último una vez sepamos que el candidato completa el resultado pasamos a guardarlo en el resultado. Si el objeto completo iguala o no supera el peso máximo lo metemos sin fraccionar. En otro caso metemos una fracción hasta completar el peso máximo:
function guardar(resultado, candidato){
if (resultado.pesoMochila + resultado.conjunto.pesos[candidato] <= resultado.conjunto.pesoMaximo){
resultado.fracciones[candidato] = 1;
resultado.pesoMochila += resultado.conjunto.pesos[candidato];
} else {
resultado.fracciones[candidato] = (resultado.conjunto.pesoMaximo - resultado.pesoMochila) / resultado.conjunto.pesos[candidato];
resultado.pesoMochila = resultado.conjunto.pesoMaximo;
}
return resultado;
}
Con todo lo anterior implementamos el siguiente ejemplo:
Ejemplo: Mochila fraccionable (teórica)
llenarMochila(pesoMaximo, pesos, valores): Implementación práctica del problema de la mochila fraccionable
El hecho de que exista un algoritmo básico como el que hemos visto voraz(conjunto) no significa que debamos seguir al pie de la letra su implementación. Si el problema no es complejo de desarrollar, es preferible evitar el exceso de funciones accesorias e ir directamente a plantear la solución en un único algoritmo.
En lo visto en el apartado anterior podemos concluir estos principios:
- Los elementos del conjunto son los propios objetos, por lo que iterar por el conjunto es iterar por ellos.
- La condición para seleccionar un objeto estriba en el precio del mismo, que es la relación valor/peso.
- El resultado puede ser simplemente un array cuya longitud es el total de objetos, array que contendrá fracciones [0, 1] de cada objeto.
Con esto podemos desarrollar un código más sencillo para el algoritmo voraz:
function llenarMochila(pesoMaximo=0, pesos=[], valores=[]){
let n = pesos.length;
numIter += 1 + 3*n + n * Math.log2(n);
let fracciones = valores.map(v => 0);
let precios = valores.map((v,i) => [i, v/pesos[i]]).
sort((a, b) => b[1]-a[1]).map(v => v[0]);
let pesoMochila = 0;
for (let j=0; j<precios.length; j++){
numIter++;
let i = precios[j];
if (pesoMochila+pesos[i]<=pesoMaximo){
fracciones[i] = 1;
pesoMochila += pesos[i];
} else {
fracciones[i] = (pesoMaximo - pesoMochila) / pesos[i];
pesoMochila = pesoMaximo;
}
if (pesoMochila===pesoMaximo) break;
}
return fracciones;
}Guardaremos el resultado en el array fracciones, para lo cual podemos tomar pesos o valores para crear un array de la misma longitud con valores iniciales cero. Crearemos un array precios con los índices de los objetos ordenado descendente por la relación valor/peso. En el acumulador pesoMochila iremos guardando el peso de la mochila. Iteramos por el array de precios que empezará con los de mayor valor, guardando bien objetos completos o, finalmente, una fracción del mismo. Salimos del bucle cuando obtengamos el peso máximo.
En el código anterior hemos agregado el contador de iteraciones numIter que nos servirá para calcular el coste y que explicaremos más abajo.
Ejemplo: Mochila fraccionable
llenarMochila(pesoMaximo, pesos, valores): Obviamente este algoritmo simplifica el visto en el apartado anterior. Pero esto no debe apartarnos de que está implícitamente presente el algoritmo básico del voraz:
- El conjunto son los índices del array de precios, que a su vez son los índices de los objetos.
- El resultado se almacenará en el array
fracciones. - El bucle que itera por los elementos del conjunto es ahora un
forque itera por el array de precios. - La selección del candidato está ímplicita en el ordenamiento descendente del array de precios.
- La comprobación si es solución el resultado la hacemos comprobando que el peso de la mochila es igual que el peso máximo.
- La comprobación de si el conjunto está vacío está implícita en el recorrido del bucle
for. - La selección del candidato está implícita en el ordenamiento del array precios.
- La comprobación de si es completable no es necesaria, pues cualquier candidato seleccionado completará la solución.
- La acción para guardar el resultado se implementa igual que la vista en la función accesoria del apartado anterior.
En cuanto al coste de este algoritmo tenemos a la entrada la creación de los array de fracciones y precios. El de fracciones usa el método map() que tiene un coste de la longitud del array. Si la longitud de pesos o valores es n, entonces ese coste de crear el array de fracciones será 1 + n donde agregamos un uno para el coste de la cabecera (ver definir la recurrencia del coste). En secuencia con lo anterior tenemos la creación del array de precios. Son dos map() y un sort(). El ordenamiento de un array tiene un coste de n log(n) cuando se usan los algoritmos más eficientes. Por lo tanto esta parte tiene un coste de 2 n + n log(n). Finalmente el bucle for tiene una longitud n en el peor de los casos.
En resumen el coste final será 1 + 4n + n log(n), donde el término n log(n) para ordenar el array de precios es el que domina y por tanto decide el coste asintótico O(n log n).
Tres tipos de mochilas
La forma en que podemos seleccionar n objetos con peso pi y valor vi para cargarlos en una mochila con un peso máximo P de tal forma que obtengamos el valor máximo V puede dar lugar a tres tipos de problemas:
- Mochila fraccionable que maximice V donde los objetos no pueden repetirse y pueden fraccionarse para completar el peso máximo P. Es el caso que nos ha ocupado este tema que se resuelve con un algoritmo voraz.
- Mochila discreta 0-1 que maximice V donde los objetos no pueden repetirse y NO pueden fraccionarse para completar un peso que no supere el máximo P. Se resuelve con programación dinámica.
- Mochila discreta 0-∞ que maximice V donde los objetos SI pueden repetirse y NO pueden fraccionarse para completar un peso que no supere el máximo P. Se resuelve con un algoritmo vuelta atrás.
Si intentáramos resolver el segundo caso de la mochila discreta 0-1 con el algoritmo voraz veríamos que no obtenemos la solución óptima. Iríamos al código y anularíamos la parte que agrega una fracción de objeto:
if (pesoMochila+pesos[i]<=pesoMaximo){
fracciones[i] = 1;
pesoMochila += pesos[i];
} else {
//fracciones[i] = (pesoMaximo - pesoMochila) / pesos[i];
//pesoMochila = pesoMaximo;
}
El resultado obtenido sería la misma tabla que en el ejemplo anterior, donde el peso máximo P era de 8 kg, no seleccionándose ahora el objeto con índice 2 pues superaría el peso máximo:
| Índice | Peso | Valor | Precio | Fracción |
|---|---|---|---|---|
| 0 | 4 | 10 | 2.5 | 0 |
| 1 | 3 | 40 | 13.333 | 1 |
| 2 | 5 | 30 | 6 | 0 |
| 3 | 2 | 20 | 10 | 1 |
Los objetos seleccionados serían los de índices 1 y 3 con un valor total V = 40+20 = 60. Pero existe una solución óptima que es seleccionar los objetos 1 y 2 que resulta un peso 8 kg que no supera P y con un valor V = 40+30 = 70 mejor que el anterior. Para resolver este tipo de problema se necesita aplicar otra técnica diferente como la programacion dinámica, algo que dejaremos para otro momento.
En cuanto al tercer caso de una mochila discreta 0-∞ se usa un vuelta atrás o backtracking para obtener la solución óptima. Es el problema más díficil de resolver puesto que no queda más remedio que ir iterando por todas las posibilidades hasta encontrar la óptima. Lo vimos cuando expusimos los temas sobre recursivos, siendo este vuelta atrás una de las situaciones donde puede utilizarse un algoritmo recursivo.
Demostración de la optimalidad de la mochila fraccionable
Intentaremos demostrar que la solución con los objetos ordenados por la relación de precio es óptima para la mochila fraccionable. Esta demostración se basa en la que aparece en el libro Fundamentos de Algoritmia de G.Brassard, P.Bratley.
Empezamos declarando que los objetos se relación en una lista de precios en orden descendente:
v1 / p1 ≥ v2 / p2 ≥ v3 / p3 ≥ ... ≥ vn / pnSea X = (x1, x2, ..., xn) la solución supuestamente óptima que se obtiene con el voraz. Si todos los xi = 1 entonces esta solución es óptima pues no hay forma de mejorarla. En otro caso habrán unos primeros objetos que se seleccionan enteros y otro siguiente que se selecciona una parte para completar el peso, tras lo cual le siguen otros que no haría falta seleccionarlos pues ya alcanzamos el peso máximo. Es decir, podríamos tener la siguiente selección para completar el peso máximo P:
P = p1 + p2 + ... + pj-1 + x pj + 0 pj+1 + ...+ 0 pnDe forma general diríamos que el peso máximo y el valor obtenido serán de la siguiente forma:
P = ∑i=1..n xi pi V = ∑i=1..n xi vi ∀i ∈ [1, j-1] ⇒ xi = 1 Cuando i = j ⇒ 0 < xi < 1 ∀i ∈ [j+1, n] ⇒ xi = 0Supongamos que encontramos otra solución Y = (y1, y2, ..., yn) con el mismo voraz. El peso máximo será el mismo P que completa la mochila, mientras que denominaremos V' como el valor de esta solución:
P = ∑i=1..n yi pi V' = ∑i=1..n yi viTenemos que demostrar que V ≥ V' (o lo que es lo mismo V - V' ≥ 0) de tal forma que X es la solución óptima que consigue el mayor valor. Dado que conocemos los valores xi para los tramos [1, j-1] y [j+1, n], aunque no conozcamos los valores yi sabemos que 0≤yi≤1 por lo que podemos afirmar lo siguiente:
∀i ∈ [1, j-1] ⇒ xi = 1 ⇒ xi ≥ yi ⇒ xi - yi ≥ 0 ∀i ∈ [j+1, n] ⇒ xi = 0 ⇒ xi ≤ yi ⇒ xi - yi ≤ 0Además tal como definimos la relación de orden descendente de precios podemos afirmar lo siguiente combinándolo con lo anterior y recordando que en las inecuaciones si a ≤ b entonces al multiplicar en ambos lados por un negativo (-c) hemos de cambiar el sentido de la inecuación quedando (-c) a ≥ (-c) b:
∀i ∈ [1, j-1] ⇒ xi - yi ≥ 0 ∧ vi / pi ≥ vj / pj ⇒ (xi - yi) vi / pi ≥ (xi - yi) vj / pj ∀i ∈ [j+1, n] ⇒ xi - yi ≤ 0 ∧ vi / pi ≤ vj / pj ⇒ (xi - yi) vi / pi ≥ (xi - yi) vj / pjEntonces vemos que para todo valor se cumple (xi - yi) vi / pi ≥ (xi - yi) vj / pj. Esto se cumple incluso cuando i = j puesto que en este caso vi / pi = vj / pj y lo anterior será ahora una igualdad más que evidente (xj - yj) vj / pj = (xj - yj) vj / pj. Con esto podemos ver a donde nos lleva la diferencia V - V':
V - V' = ∑i=1..n (xi - yi) vi = ∑i=1..n (xi - yi) pi (vi / pi) ≥ ∑i=1..n (xi - yi) pi (vj / pj)Dado que vj / pj es independiente del rango del sumatorio podemos ponerlo por fuera. Además separaremos el sumatorio para los valores de X e Y:
V - V' ≥ (vj / pj) ∑i=1..n (xi - yi) pi = (vj / pj) ( ∑i=1..n xi pi - ∑i=1..n yi pi )Recordando que ambas soluciones X e Y consiguen completar el peso máximo P nos queda:
V - V' ≥ (vj / pj) (P-P) = 0Finalmente vemos que V - V' ≥ 0 por lo que V ≥ V' siendo la solución X la óptima que consigue el mayor valor de la mochila fraccionable.