Cliques en grafos
Obtener todos los cliques en un grafo getAllCliques()
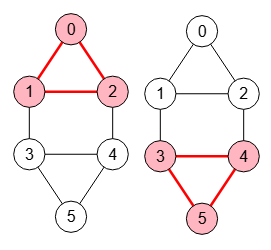
Un clique en un grafo es un subconjunto de nodos tal que cada par de nodos está conectado. En la Figura vemos que el grafo sólo tiene dos cliques con tamaño mayor que 2, pues las aristas de "0,1,2" o "3,4,5" conectan todos esos vértices. Sin embargo "1,2,3,4" no es un clique pues no hay arista entre todos esos vértices, pues faltarían las aristas "1-4" y "2-3".
El tamaño de un clique es su número de nodos. Los de tamaño 1 son los propios nodos y los de tamaño 2 las aristas. En los algoritmos que implementamos tenemos una opción para ignorar estos tamaños 1 y 2 pues parecen obvios, pero no debemos olvidar que también son cliques.
En el tema anterior vimos como obtener un subgrafo inducido que era un subconjunto de nodos con todas sus aristas incidentes. Pues bien, cuando ese subgrafo inducido es también completo entonces es un clique. Y esto es lo que aplicamos en el algoritmo getAllCliques() que veremos después, usando getInducedSubgraph() y isGraphComplete().
Obtener todos los cliques: [[0,1,2],[3,4,5]]
La aplicación nos devuelve los cliques como listas de nodos. Con el siguiente JSON puede importar ese ejemplo.
{"nodes":[
{"index":0,"parent":[{"index":-1}]},
{"index":1,"parent":[{"index":0}]},
{"index":2,"parent":[{"index":0},{"index":1}]},
{"index":3,"parent":[{"index":1}]},
{"index":4,"parent":[{"index":2},{"index":3}]},
{"index":5,"parent":[{"index":3},{"index":4}]}
],
"config":{
"algorithm":"Get all cliques"
}}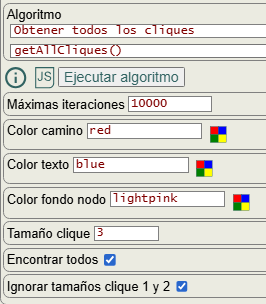
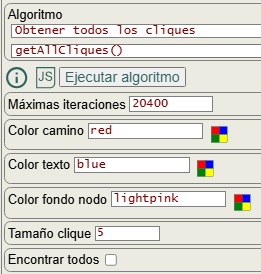
En la Figura vemos las opciones para obtener todos los cliques. Con la opción tamaño clique seleccionamos entre 1 y el número de nodos del grafo. Con encontrar todos desmarcado nos devolverá todos los cliques del tamaño especificado. Si está marcado buscará todos los cliques de cualquier tamaño, a excepción de los tamaños 1 y 2 que se pueden ignorar como cliques en caso de que la opción ignorar tamaños clique 1 y 2 esté marcada.
Las opciones color camino, color texto y color fondo nodo no se pasan al algoritmo pues se aplican posteriormente sólo para resaltar el clique en el grafo.
Marcando la opción encontrar todos y desmarcando ignorar tamaños clique 1 y 2 encontrará también los de tamaño 1 (vértices) y tamaño 2 (aristas):
Obtener todos los cliques: [[0],[1],[2],[3],[4],[5], [0,1],[0,2],[1,2],[1,3],[2,4],[3,4], [3,5],[4,5], [0,1,2],[3,4,5]]
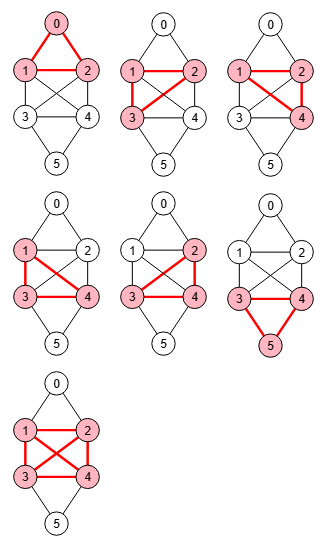
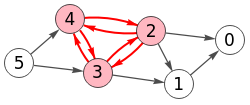
Agregando las aristas "1-4" y "2-3" al ejemplo de antes entonces obtenemos 7 cliques (encontrando todos e ignorando tamaños 1 y 2), como se observa en la Figura. Los seis primeros son de tamaño 3 y el último de tamaño 4.
Obtener todos los cliques: [[0,1,2],[1,2,3],[1,2,4],[1,3,4], [2,3,4],[3,4,5],[1,2,3,4]]
{"nodes":[
{"index":0,"parent":[{"index":-1}]},
{"index":1,"parent":[{"index":0}]},
{"index":2,"parent":[{"index":0},{"index":1}]},
{"index":3,"parent":[{"index":1},{"index":2}]},
{"index":4,"parent":[{"index":2},{"index":3},{"index":1}]},
{"index":5,"parent":[{"index":3},{"index":4}]}
],
"config":{
"lineHeight":18.75,
"algorithm":"Get all cliques",
"findAll":true
}}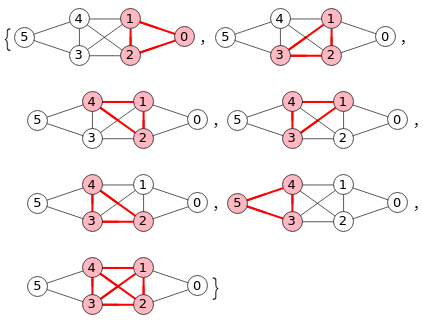
En la Figura vemos en Wolfram todos los cliques con tamaño >2 obteniendo el mismo resultado que en nuestra aplicación. Wolfram no dispone de una función específica para encontrar cliques, pues FindClique sólo sirve para encontrar cliques máximos y maximales, como veremos después.
Wolfram define un clique como un conjunto maximal de nodos donde el correspondiente subgrafo es completo. Es posible también obtener los máximos, pero en ningún caso devolverá cliques de otros tamaños que no sean máximos o maximales. Para obtener todos los cliques hacemos lo mismo que en nuestro algoritmo, como veremos después. Estos son los pasos del código en Wolfram que hemos construido:
- Obtenemos todos los vértices con
v = VertexList[g] - Obtenemos todas las combinaciones de vértices con
c = Subsets[v,{3,Infinity}]filtrando para los tamaños que se especifiquen. En el ejemplo vamos a encontrar todas las combinaciones de vértices de tamaño mayor que 2 - Obtenemos los subgrafos inducidos de esas combinaciones de vértices con
d = Table[Subgraph[g, i], {i,c}] - Filtramos aquellos subgrafos que sean completos con
s = Select[d,CompleteGraphQ[#]&] - Finalmente resaltamos los cliques de
s
g = AdjacencyGraph[{{0,1,1,0,0,0},{1,0,1,1,1,0},{1,1,0,1,1,0},{0,1,1,0,1,1},{0,1,1,1,0,1},{0,0,0,1,1,0}}, ImageSize -> 188, VertexSize -> {"Scaled", 0.12},
VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center], 3 -> Placed[2,Center], 4 -> Placed[3,Center], 5 -> Placed[4,Center], 6 -> Placed[5,Center]},
VertexLabelStyle -> Directive[Black,13.13], EdgeLabelStyle -> Directive[Black,13.13,Bold], VertexStyle -> White, EdgeStyle -> {{Black,Thickness[0.005]}}];
v = VertexList[g];
c = Subsets[v, {3,Infinity}];
d = Table[Subgraph[g, i], {i,c}];
s = Select[d, CompleteGraphQ[#]&];
Table[HighlightGraph[g,{Style[VertexList[i], RGBColor["lightpink"]], Style[EdgeList[i], Red, Thick], Annotation[EdgeList[i], EdgeLabelStyle->Directive[Blue,13.13,Bold]]}], {i,s}]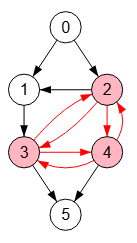
En la Figura vemos el clique de mayor tamaño en un grafo dirigido, obteniéndose los siguiente cliques totales:
Obtener todos los cliques: [[0],[1],[2],[3],[4],[5], [2,3],[2,4],[3,4], [2,3,4]]
Los cliques serán los nodos individuales y el resto deberán formarse con aristas doblemente dirigidas necesariamente, como son las aristas "2🡘3", "2🡘4" y "3🡘4", que son cliques de tamaño 2. Y con ellas se forma el clique de tamaño 3 mostrado.
{"nodes":[
{"index":0,"nodeOffset":"16.67","parent":[{"index":-1}]},
{"index":1,"parent":[{"index":0}]},
{"index":2,"parent":[{"index":0},{"index":3,"lineType":"quadratic","lineOffset":"0 1.5"},{"index":4},{"index":1}]},
{"index":3,"nodeOffset":"-16.67","parent":[{"index":1},{"index":2,"lineType":"quadratic","lineOffset":"0 -1.5"},{"index":4}]},
{"index":4,"nodeOffset":"0 50","parent":[{"index":2,"lineType":"quadratic","lineOffset":"2"},{"index":3,"lineType":"quadratic","lineOffset":"0 2"}]},
{"index":5,"parent":[{"index":3},{"index":4}]}
],
"config":{
"markerEnd":"arrow",
"algorithm":"Get all cliques",
"findAll":true,
"ignoreSizeClique12":false
}}
En la Figura vemos el mismo resultado alcanzado en Wolfram para el de mayor tamaño devolviendo también todos los mismos cliques.
g = AdjacencyGraph[{{0,0,0,0,0,0},{1,0,0,0,0,0},{1,1,0,1,1,0},{0,1,1,0,1,0},{0,0,1,1,0,0},{0,0,0,1,1,0}}, ImageSize -> 250, VertexSize -> {"Scaled", 0.13},
VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center], 3 -> Placed[2,Center], 4 -> Placed[3,Center], 5 -> Placed[4,Center], 6 -> Placed[5,Center]},
VertexLabelStyle -> Directive[Black,17.5], EdgeLabelStyle -> Directive[Black,17.5,Bold], VertexStyle -> White, DirectedEdges -> True, EdgeStyle -> {{Black,Thickness[0.005]}}];
v = VertexList[g];
c = Subsets[v, {1,Infinity}];
d = Table[Subgraph[g, i], {i,c}];
s = Select[d, CompleteGraphQ[#]&];
Table[HighlightGraph[g,{Style[VertexList[i], RGBColor["lightpink"]], Style[EdgeList[i], Red, Thick], Annotation[EdgeList[i], EdgeLabelStyle->Directive[Blue,17.5,Bold]]}], {i,s}]El JavaScript para ejecutar el algoritmo getAllCliques() se muestra a continuación. Usa getInducedSubgraph() para obtener el subgrafo inducido de una lista de nodos. Y isGraphComplete() para saber si ese subgrafo es completo.
function getAllCliques({matrix=[], sizeClique=3, findAll=false, ignoreSizeClique12=true}) {
let result = [];
try {
let n = matrix.length;
let minSize = findAll && ignoreSizeClique12 ? 3 : 1;
sizeClique = Math.max(minSize, Math.min(sizeClique, n));
let indexes = Array.from({length: n}, (v,i) => i);
let [from, to] = findAll ? [minSize, n] : [sizeClique, sizeClique];
for (let j=from; j<=to; j++) {
iter = 0;
let lists = combine(indexes, j);
if (typeof lists==="string") throw new Error(lists);
if (lists.hasOwnProperty("warning")) {
result.warnings = [lists.warning];
break;
}
for (let list of lists) {
let minor = getInducedSubgraph({matrix, indexesSubgraph: list});
if (typeof minor==="string") throw new Error(minor);
let ok = isGraphComplete({matrix: minor});
if (typeof ok==="string") throw new Error(ok);
if (ok) result.push(list);
}
}
} catch(e){result = e.message}
return result;
}El funcionamiento se basa en obtener todas las combinaciones de nodos, obtener el subgrafo inducido por cada combinación y si ese subgrafo es completo entonces es un clique. Si especificamos un tamaño a buscar en sizeClique y encontrar todos con findAll es falso, entonces busca todas las combinaciones de nodos de ese tamaño. Si findAll es verdadero entonces busca en todos los tamaños desde minSize hasta el total de nodos. Si ignoramos tamaños 1 y 2 con ignoreSizeClique12 empezaremos en minSize = 3 y en otro caso en 1.
El algoritmo para buscar las combinaciones es el siguiente, que es una adaptación del que presentamos en el tema combinaciones sin repetición: algoritmo mejorado. La adaptación se refiere a no cortar el algoritmo cuando se llegue al máximo de iteraciones, sino devolver un aviso warning y los resultados alcanzados hasta el momento.
function combine(list=[], k=0, n=list.length, res=Array.from({length:k}, ()=>""),
result=[], n0=list.length, k0=res.length){
try {
if (iter++, iter>maxIter) {
result.warning = `Maximum iterations '${maxIter}' reached in combine() with n='${n0}' and k='${k0}'`;
return result;
}
if (k===0){
result.push([...res]);
} else {
for (let j=n; j>=k; j--){
res[k0-k] = list[n0-j];
combine(list, k-1, j-1, res, result);
}
}
} catch(e) {result = e.message}
return result;
}Limitaciones de los algoritmos que se basan en la combinaciones
Como dice la página de Wikipedia sobre Clique problem, obtener los cliques requiere en general tiempos exponenciales, pues la sistemática es inspeccionar todos los subconjuntos de nodos, tarea del tipo fuerza bruta que llegar a ser computacionalmente intratable cuando el número de nodos empieza a tener cierto tamaño. No se conoce algoritmo con tiempo polinomial para el problema general, aunque para ciertos tipos de grafos se han estudiado algunos más eficientes.
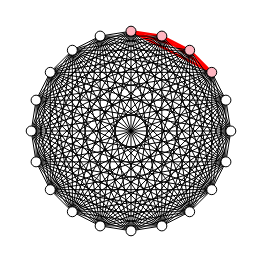
En la Figura vemos un grafo completo con 20 nodos presentándose el primer clique de los 4845 de tamaño 4 que tiene el algoritmo, consumiendo 8 ms. El resultado los devuelve todos, como vemos a continuación donde hemos abreviado con puntos suspensivos.
Time: 8 ms Obtener todos los cliques: [[0,1,2,3],[0,1,2,4],[0,1,2,5],[0,1,2,6],[0,1,2,7],[0,1,2,8],[0,1,2,9],[0,1,2,10], [0,1,2,11],[0,1,2,12],[0,1,2,13],[0,1,2,14],[0,1,2,15],[0,1,2,16],[0,1,2,17],[0,1,2,18], ... [14,15,17,18],[14,15,17,19],[14,15,18,19],[14,16,17,18],[14,16,17,19],[14,16,18,19], [14,17,18,19],[15,16,17,18],[15,16,17,19],[15,16,18,19],[15,17,18,19],[16,17,18,19]]
Con este JSON puede importar el ejemplo.
{"nodes":[
{"index":0,"nodeOffset":"2.5","parent":-1},
{"index":1,"nodeOffset":"59.86 -23.04","parent":0},
{"index":2,"nodeOffset":"66.01 -17.36","parent":[0,1]},
{"index":3,"nodeOffset":"69.86 -8.51","parent":[0,1,2]},
{"index":4,"nodeOffset":"70.54 2.64","parent":[0,1,2,3]},
{"index":5,"nodeOffset":"67.5 15","parent":[0,1,2,3,4]},
{"index":6,"nodeOffset":"60.54 27.36","parent":[0,1,2,3,4,5]},
{"index":7,"nodeOffset":"49.86 38.51","parent":[0,1,2,3,4,5,6]},
{"index":8,"nodeOffset":"36.01 47.36","parent":[0,1,2,3,4,5,6,7]},
{"index":9,"nodeOffset":"19.86 53.04","parent":[0,1,2,3,4,5,6,7,8]},
{"index":10,"nodeOffset":"2.5 55","parent":[0,1,2,3,4,5,6,7,8,9]},
{"index":11,"nodeOffset":"-14.86 53.04","parent":[0,1,2,3,4,5,6,7,8,9,10]},
{"index":12,"nodeOffset":"-31.01 47.36","parent":[0,1,2,3,4,5,6,7,8,9,10,11]},
{"index":13,"nodeOffset":"-44.86 38.51","parent":[0,1,2,3,4,5,6,7,8,9,10,11,12]},
{"index":14,"nodeOffset":"-55.54 27.36","parent":[0,1,2,3,4,5,6,7,8,9,10,11,12,13]},
{"index":15,"nodeOffset":"-62.5 15","parent":[0,1,2,3,4,5,6,7,8,9,10,11,12,13,14]},
{"index":16,"nodeOffset":"-65.54 2.64","parent":[0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]},
{"index":17,"nodeOffset":"-64.86 -8.51","parent":[0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]},
{"index":18,"nodeOffset":"-61.01 -17.36","parent":[0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17]},
{"index":19,"nodeOffset":"-54.86 -23.04","parent":[0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18]}
],
"config":{
"nodeValueAuto":"none",
"nodeRadius":2,
"algorithm":"Get all cliques",
"sizeClique":4
}}
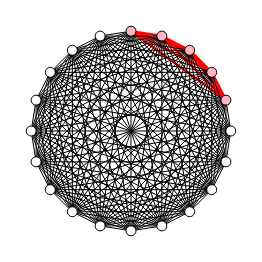
Si tratamos de obtener las 15504 de tamaño 5 la aplicación nos dará el mensaje de error Máximas iteraciones '10000' alcanzadas en combine() con n='20' y k='5'. El algoritmo itera extrayendo las combinaciones de 20 nodos tomados desde k=1 hasta k=20, viendo que cuando llegó a 5 consumió las 10000 iteraciones que por defecto se establecen en los algoritmos para evitar tiempo excesivo y que se colapse el navegador. Así que para obtener los de tamaño 5 se necesitan 20400 iteraciones, obteniéndose los cliques de ese tamaño como vemos en la Figura que presenta el primero de ellos.
Obviamente en un grafo completo cualquier subconjunto de nodos es obligatoriamente un clique, puesto que hay aristas entre todos los nodos. Pero vamos a usar este tipo de grafo para resaltar que el problema tiene un coste exponencial. Suponiendo que tenemos un grafo cualquiera y tratamos de buscar los cliques de mayor tamaño, como veremos en el siguiente apartado, hemos de iterar por todos los tamaños desde el mayor hasta encontrar un subconjunto de nodos que forme un clique.
Si pensamos en un grafo con 20 nodos y el clique máximo tiene 3 nodos, no hay otra forma que empezar con tamaño 20 e ir descendiendo hasta llegar a uno de tamaño 3, momento en el que finalizaríamos devolviendo ese clique. Y eso supone hallar todas las listas de combinaciones C(20, 20), C(20, 19), ..., C(20, 3) y por cada combinación de cada lista formar el grafo inducido y comprobar si es completo.
Las combinaciones se denotan como (nk) o simplemente como C(n, k). En un grafo completo con n nodos hay C(n, k) cliques de tamaño k. Y hay ∑k=1..n C(n, k) = 2n - 1 cliques con tamaños de 1 a n, con lo que para n = 20 ese número es de 1048575 resultados. Se necesitan 400000 iteraciones para obtener todos los cliques en un tiempo superior a 4 segundos, como se observa en el siguiente resultado obtenido en la aplicación, abreviando resultados con puntos suspensivos. Vea que el último clique contiene todos los nodos, pues el propio grafo al ser completo es también uno de los cliques, el de mayor tamaño.
Time: 4303 ms
Obtener todos los cliques: [
[0],
[1],
[2],
...
[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19],
[0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]
]
"··· recortado a 1000000 caracteres" recortando las últimas posiciones del resultado hasta alcanzar el tamaño especificado en la cofiguración. Para mostrarlos todos ponemos 30 en ese campo para mostrar hasta 30 millones. Un exceso puede producir ralentización o incluso colapso de la página.En la aplicación Combine Tools puede obtenerse la siguiente tabla de valores en la pestaña "Numéricos" para C(20, k) con 1 ≤ k ≤ 20, observando que hay 4845 combinaciones con k=4 y 15504 con k=5:
| n↓k→ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 20 | 20 | 190 | 1140 | 4845 | 15504 | 38760 | 77520 | 125970 | 167960 | 184756 | 167960 | 125970 | 77520 | 38760 | 15504 | 4845 | 1140 | 190 | 20 | 1 |
En el tema combinaciones sin repetición: algoritmo mejorado se explica el algoritmo que estamos usando para obtener las combinaciones. Se expone que el coste de ese algoritmo es el siguiente:
n≥k ⇒ T(n, k) = 2 C(n+1, k) - 1 + k + k C(n, k)
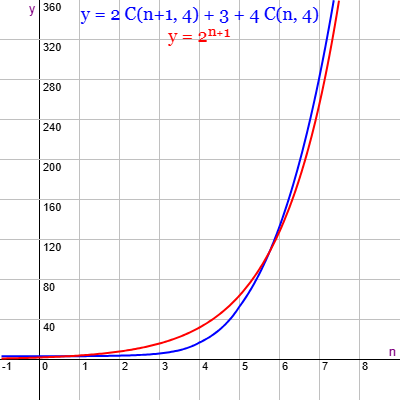
Como en nuestro caso siempre n≥k, representamos esa función para k=4 en la gráfica matemática de la Figura, donde se observa su caracter exponencial. También representamos y = 2n+1 que se asimila bastante, donde ya no cabe duda de ese caracter exponencial
edita-funcion: y = 2 * (factorial(x+1) / (factorial(4)*factorial(x+1-4))) + 3 + 4 * (factorial(x) / (factorial(4)*factorial(x-4))); color= 'blue'; # y = 2**(x+1); color = 'red'; _zoomy: 1 _movex: -4.000 _movey: -160 _color-ejes: black _num-decimales-ejes: 0 _titulo-x: n _font-size-titulos: 13 _titulo-grafica: y = 2 C(n+1, 4) + 3 + 4 C(n, 4) y = 2ⁿ⁺¹ _posicion-titulo-grafica: top-center _colores-titulo-grafica: blue,red _contorno: 1
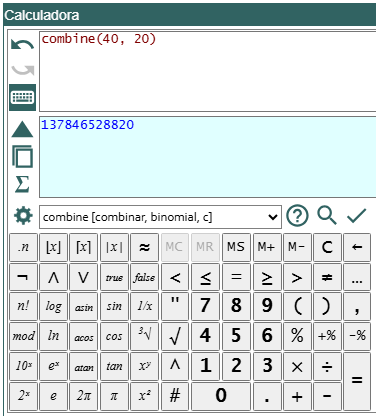
Si subimos de 20 nodos el problema empieza a ser intratable. Por ejemplo, con 40 nodos vemos en la Figura el resultado C(40, 20) = 137 846 528 820 combinaciones, valor obtenido en la aplicación de la calculadora. Ese número de combinaciones es fácil de calcular, pero sería intratable para una aplicación que tuviera que manejar tal número de conjuntos.
Así que no necesitamos grafos muy grandes para empezar a tener problemas de eficiencia con los algoritmos que se basan en combinaciones.
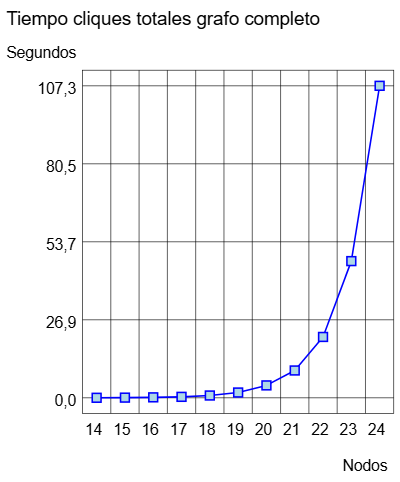
Obteniendo en la aplicación de grafos todos los cliques en grafos completos desde 14 a 24 nodos vemos en la siguiente tabla las iteraciones necesarias (en miles) y los milisegundos que consumió el algoritmo. En la gráfica adjunta de la Figura se presentan los tiempos de ejecución en segundos, observando el caracter exponencial.
Nodos Iter ms 14 7 50 15 13 97 16 25 193 17 49 366 18 95 830 19 190 1857 20 400 4299 21 750 9436 22 1400 20967 23 2750 47034 24 5500 107315
{"values": [
["Nodos", "Segundos"],
["14", 0.05],
["15", 0.097],
["16", 0.193],
["17", 0.366],
["18", 0.83],
["19", 1.857],
["20", 4.299],
["21", 9.436],
["22", 20.967],
["23", 47.034],
["24", 107.315]
],
"config": {
"svgType": "line",
"title": "Tiempo cliques totales grafo completo",
"titleFontSize": 6,
"legend": "none",
"xAxisRotation": 0,
"yLabel": "Segundos",
"gridSplit": 4
}}Obtener cliques máximos en un grafo getMaximumCliques()
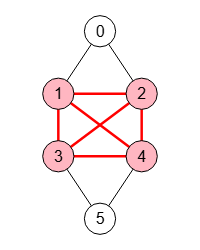
Un cliqué máximo es el que tiene el mayor número de nodos entre todos los cliques posibles. En la Figura vemos el clique máximo de tamaño 4. Si recordamos todos los cliques mayores de 2 que vimos en la Figura, este era el único de mayor tamaño.
Obtener máximos cliques: [[1,2,3,4]]
La aplicación devuelve este resultado. Con el JSON siguiente puede importar ese ejemplo.
{"nodes":[
{"index":0,"parent":[{"index":-1}]},
{"index":1,"parent":[{"index":0}]},
{"index":2,"parent":[{"index":0},{"index":1}]},
{"index":3,"parent":[{"index":1},{"index":2}]},
{"index":4,"parent":[{"index":2},{"index":3},{"index":1}]},
{"index":5,"parent":[{"index":3},{"index":4}]}
],
"config":{
"nodeOffset":"-10",
"algorithm":"Get maximum cliques"
}}
En la Figura vemos que no hay opciones para ejecutar el algoritmo getMaximumCliques(), pues color camino, color texto y color fondo nodo se aplican posteriormente a su ejecución sólo para resaltar los cliques en el grafo.
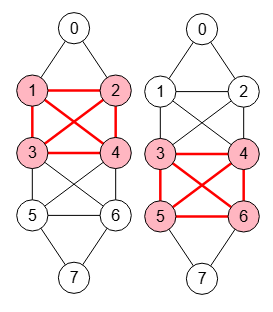
El algoritmo devuelve todos los máximos del mismo tamaño. En la Figura vemos que hay dos de tamaño máximo 4.
Obtener máximos cliques: [[1,2,3,4],[3,4,5,6]]
{"nodes":[
{"index":0,"parent":[{"index":-1}]},
{"index":1,"parent":[{"index":0}]},
{"index":2,"parent":[{"index":0},{"index":1}]},
{"index":3,"parent":[{"index":1},{"index":2}]},
{"index":4,"parent":[{"index":2},{"index":3},{"index":1}]},
{"index":5,"parent":[{"index":3},{"index":4}]},
{"index":6,"parent":[{"index":3},{"index":5},{"index":4}]},
{"index":7,"parent":[{"index":5},{"index":6}]}
],
"config":{
"algorithm":"Get maximum cliques"
}}
Wolfram define un clique como un conjunto maximal de nodos donde el correspondiente subgrafo es completo, como se observa en la página de la función FindClique.
Y nosotros con getAllCliques() los contemplamos todos, sean o no máximos o maximales. Con getMaximumCliques() lo que hacemos es obtener todos los cliques con getAllCliques() desde el tamaño de nodos del grafo hasta 1, de tal forma que cuando encontremos cliques en un tamaño los devolveremos y finalizaremos, siendo esos los máximos.
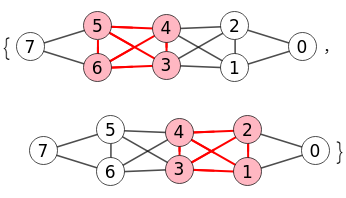
Expone Wolfram que con FindClique[g, Length /@ FindClique[g], All] podemos obtener todos los cliques máximos, devolviendo {{4,5,6,7},{2,3,4,5}} que son los mismos que obtuvimos teniendo en cuenta que los índices se inician en 1. En la Figura vemos que se obtiene el mismo resultado.
g = AdjacencyGraph[{{0,1,1,0,0,0,0,0},{1,0,1,1,1,0,0,0},{1,1,0,1,1,0,0,0},{0,1,1,0,1,1,1,0},{0,1,1,1,0,1,1,0},{0,0,0,1,1,0,1,1},{0,0,0,1,1,1,0,1},{0,0,0,0,0,1,1,0}},
ImageSize -> 313, VertexSize -> {"Scaled", 0.1}, VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center], 3 -> Placed[2,Center],
4 -> Placed[3,Center], 5 -> Placed[4,Center], 6 -> Placed[5,Center], 7 -> Placed[6,Center], 8 -> Placed[7,Center]}, VertexLabelStyle -> Directive[Black,17.5],
EdgeLabelStyle -> Directive[Black,17.5,Bold], VertexStyle -> White, EdgeStyle -> {{Black,Thickness[0.005]}}];
f = FindClique[g, Length /@ FindClique[g], All];
s = Table[Subgraph[g, i], {i,f}];
Table[HighlightGraph[g,{Style[VertexList[i], RGBColor["lightpink"]], Style[EdgeList[i], Red, Thick], Annotation[EdgeList[i], EdgeLabelStyle->Directive[Blue,17.5,Bold]]}], {i,s}]La expresión Length /@ FindClique[g] es para aplicar Length con Map y obtener el tamaño del clique máximo. Como FindClique[g] sin más argumentos encuentra un único clique máximo, con Length /@ FindClique[g] nos devolverá el tamaño {4} de ese clique, valor que trasladamos a FindClique[g, 4, All] para encontrar todos los de tamaño 4. Así que la sentencia anterior con el uso de /@ equivale estas dos:
m = Map[Length, FindClique[g]]
f = FindClique[g, m, All];
Las formas de aplicar findClique son las siguientes, tal como expone Wolfram:
- Cliques máximos
FindClique[g]encuentra un único clique máximo de un grafo "g"FindClique[g, Length/@FindClique[g], s]encuentra como mucho "s" cliques máximosFindClique[g, Length/@FindClique[g], All]encuentra todos los cliques máximos
- Cliques maximales
FindClique[g, Infinity]encuentra un único clique maximal de un grafo "g"FindClique[g, Infinity, s]encuentra como mucho "s" cliques maximalesFindClique[g, Infinity, All]encuentra todos los cliques maximales
El JavaScript para ejecutar getMaximumCliques() es el siguiente, usando getAllCliques() para obtener todos los cliques de cierto tamaño. Empezamos buscando cliques de tamaño igual que el número de nodos del grafo y vamos descendiendo hasta tamaño 1. Cuando encontremos cliques en un tamaño con getAllCliques() los devolveremos como cliques máximos.
function getMaximumCliques({matrix=[]}) {
let result = [];
try {
let n = matrix.length;
for (let j=n; j>0; j--) {
let cliques = getAllCliques({matrix, sizeClique:j, findAll:false});
if (typeof cliques==="string") throw new Error(cliques);
if (cliques.hasOwnProperty("warnings")) {
result.warnings = cliques.warnings;
break;
}
if (cliques.length>0) {
result.push(...cliques);
break;
}
}
} catch(e){result = e.message}
return result;
}Obtener cliques maximales Bron-Kerbosch getMaximalCliquesBronKerbosch()
Un clique maximal es un clique que no puede ser ampliado agregando uno o más nodos, significando que un clique máximal no puede ser subconjunto de un clique de mayor tamaño.
En este apartado implementaremos el algoritmo de Bron-Kerbosch para encontrar todos los cliques maximales en un grafo, tomando como base el pseudo-código que expone esa página de Wikipedia.
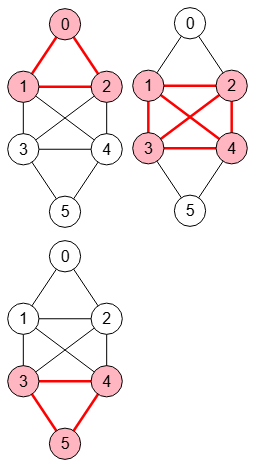
En la Figura vemos los cliques maximales de un grafo que hemos visto en apartados anteriores, obteniéndose este resultado:
Obtener cliques maximales
(Bron-Kerbosch):
{"cliques":
[[0,1,2],[1,2,3,4],[3,4,5]],
"trace":[]}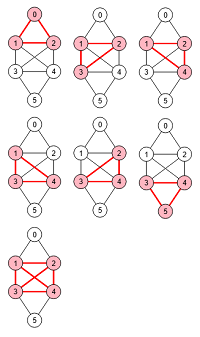
Recordemos que un cliqué máximo es el que tiene el mayor número de nodos entre todos los cliques posibles, así los cliques máximos del grafo de la Figura sólo es el segundo con 4 nodos, tal como vimos en la Figura.
En la Figura adjunta reproducimos todos los cliques del mismo grafo de tamaño mayor que 2, que vimos en Figura. Se observa que el último es un clique máximo (el único por ser el de mayor tamaño 4) y maximal al mismo tiempo, pues no forma parte de un clique mayor. Mientras que el primero y el penúltimo son maximales, pues tampoco forman parte de otro clique mayor. El resto forman parte del último clique y por tanto no son maximales.
Un clique máximo siempre es máximal, pero no necesariamente al revés. Así el de tamaño 4 es máximo y maximal, pero los dos de tamaño 3 de la Figura son maximales pero no máximos.
Sin embargo el clique maximal de mayor tamaño siempre coincidirá con el clique máximo. Así esto puede aprovecharse para encontrar el clique máximo con este algoritmo de Bron-Kerbosch que es más eficiente que los que vimos basados en las combinaciones.
Con el siguiente JSON puede importar el ejemplo.
{"nodes":[
{"index":0,"parent":[{"index":-1}]},
{"index":1,"parent":[{"index":0}]},
{"index":2,"parent":[{"index":0},{"index":1}]},
{"index":3,"parent":[{"index":1},{"index":2}]},
{"index":4,"parent":[{"index":2},{"index":3},{"index":1}]},
{"index":5,"parent":[{"index":3},{"index":4}]}
],
"config":{
"nodeOffset":"-10",
"algorithm":"Get maximal cliques (Bron-Kerbosch)"
}}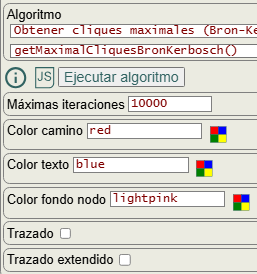
En la Figura vemos las opciones para obtener todos los cliques maximales. Las únicas opciones que se pasan al algoritmo son trazado y trazado extendido que veremos después, pues las opciones color camino, color texto y color fondo nodo no se pasan al algoritmo pues se aplican posteriormente sólo para resaltar el clique en el grafo.
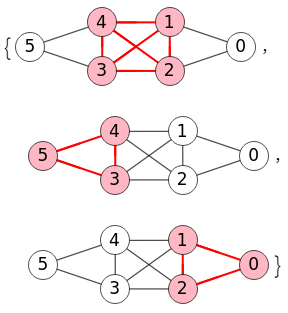
En la Figura vemos los mismos cliques maximales en Wolfram, aplicando FindClique[g, Infinity, All].
g = AdjacencyGraph[{{0,1,1,0,0,0},{1,0,1,1,1,0},{1,1,0,1,1,0},{0,1,1,0,1,1},{0,1,1,1,0,1},{0,0,0,1,1,0}}, ImageSize -> 250, VertexSize -> {"Scaled", 0.13},
VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center], 3 -> Placed[2,Center], 4 -> Placed[3,Center], 5 -> Placed[4,Center],
6 -> Placed[5,Center]}, VertexLabelStyle -> Directive[Black,17.5], EdgeLabelStyle -> Directive[Black,17.5,Bold], VertexStyle -> White,
EdgeStyle -> {{Black,Thickness[0.005]}}];
f = FindClique[g, Infinity, All];
s = Table[Subgraph[g, i], {i,f}];
Table[HighlightGraph[g,{Style[VertexList[i], RGBColor["lightpink"]], Style[EdgeList[i], Red, Thick], Annotation[EdgeList[i], EdgeLabelStyle->Directive[Blue,17.5,Bold]]}], {i,s}]Volvemos a recordar las formas de aplicar findClique, tal como expone Wolfram:
- Cliques máximos
FindClique[g]encuentra un único clique máximo de un grafo "g"FindClique[g, Length/@FindClique[g], s]encuentra como mucho "s" cliques máximosFindClique[g, Length/@FindClique[g], All]encuentra todos los cliques máximos
- Cliques maximales
FindClique[g, Infinity]encuentra un único clique maximal de un grafo "g"FindClique[g, Infinity, s]encuentra como mucho "s" cliques maximalesFindClique[g, Infinity, All]encuentra todos los cliques maximales
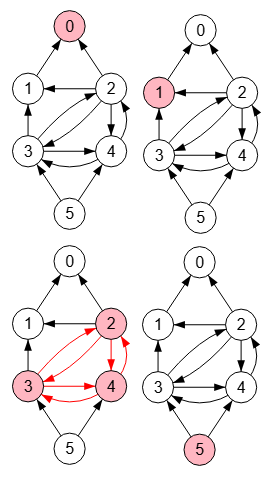
En la figura Figura vemos los cliques maximales en un grafo dirigido. En el algoritmo sólo se consideran las aristas que sean doblemente dirigidas, pues sólo esas y los nodos solitarios pueden formar clique. Si no hubieran aristas doblemente dirigidas, cada uno de los nodos sería un clique maximal.
Obtener cliques maximales
(Bron-Kerbosch):
{"cliques":[[0],[1],[2,3,4],[5]],
"trace":""}
{"nodes":[
{"index":0,"nodeOffset":"16.67","parent":[{"index":-1}]},
{"index":1,"parent":[{"index":0}]},
{"index":2,"parent":[{"index":0},{"index":3,"lineType":"quadratic","lineOffset":"0 1.5"},{"index":4},{"index":1}]},
{"index":3,"nodeOffset":"-16.67","parent":[{"index":1},{"index":2,"lineType":"quadratic","lineOffset":"0 -1.5"},{"index":4}]},
{"index":4,"nodeOffset":"0 50","parent":[{"index":2,"lineType":"quadratic","lineOffset":"2"},{"index":3,"lineType":"quadratic","lineOffset":"0 2"}]},
{"index":5,"parent":[{"index":3},{"index":4}]}
],
"config":{
"markerEnd":"arrow",
"algorithm":"Get maximal cliques (Bron-Kerbosch)"
}}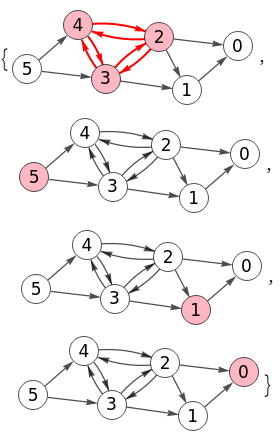
En la Figura vemos que Wolfram devuelve el mismo resultado.
g = AdjacencyGraph[{{0,0,0,0,0,0},{1,0,0,0,0,0},{1,1,0,1,1,0},{0,1,1,0,1,0},{0,0,1,1,0,0},{0,0,0,1,1,0}}, ImageSize -> 250, VertexSize -> {"Scaled", 0.13},
VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center], 3 -> Placed[2,Center], 4 -> Placed[3,Center], 5 -> Placed[4,Center], 6 -> Placed[5,Center]},
VertexLabelStyle -> Directive[Black,17.5], EdgeLabelStyle -> Directive[Black,17.5,Bold], VertexStyle -> White, DirectedEdges -> True, EdgeStyle -> {{Black,Thickness[0.005]}}];
f = FindClique[g, Infinity, All];
s = Table[Subgraph[g, i], {i,f}];
Table[HighlightGraph[g,{Style[VertexList[i], RGBColor["lightpink"]], Style[EdgeList[i], Red, Thick], Annotation[EdgeList[i], EdgeLabelStyle->Directive[Blue,17.5,Bold]]}], {i,s}]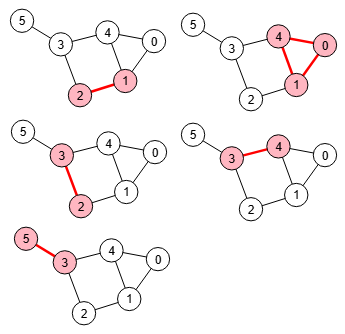
Entre las opciones de la Figura vemos trazado que marcamos, sin marcar trazado extendido. Probamos con el grafo de la Figura obteniendo este resultado que incluye una traza de ejecución del algoritmo, grafo y trazado que aparece en la página Algoritmo de Bron-Kerbosch en Wikipedia, la segunda versión con pivote (with pivoting). La traza es la misma sólo que en la de Wikipedia los índices empiezan en 1 y en nuestra aplicación en 0.
Obtener cliques maximales (Bron-Kerbosch): {
"cliques":[[1,2],[0,1,4],[2,3],[3,4],[3,5]],
"trace":"
bronKerbosch([], [0,1,2,3,4,5], [])
bronKerbosch([1], [0,2,4], [])
bronKerbosch([1,2], [], []) ⇒ Maximal: [1,2]
bronKerbosch([1,4], [0], [])
bronKerbosch([1,4,0], [], []) ⇒ Maximal: [0,1,4]
bronKerbosch([3], [2,4,5], [])
bronKerbosch([3,2], [], []) ⇒ Maximal: [2,3]
bronKerbosch([3,4], [], []) ⇒ Maximal: [3,4]
bronKerbosch([3,5], [], []) ⇒ Maximal: [3,5]
bronKerbosch([5], [], [3])
"}Con este JSON puede importar el ejemplo.
{"nodes":[
{"index":0,"nodeOffset":"32.36 14.43","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"33.67 10.85","parent":[{"index":0}]},
{"index":2,"nodeOffset":"-7.21 -6.5","parent":[{"index":1}]},
{"index":3,"nodeOffset":"-17.46 -58.84","parent":[{"index":2}]},
{"index":4,"nodeOffset":"-9.17 -15.25","parent":[{"index":0},{"index":1},{"index":3}]},
{"index":5,"nodeOffset":"-38.21 -96.51","parent":[{"index":3}]}
],
"config":{
"lineHeight":18.75,
"algorithm":"Get maximal cliques (Bron-Kerbosch)",
"tracing":true
}}El JavaScript para el algoritmo getMaximalCliquesBronKerbosch() se muestra a continuación. Hace uso de getVertexDegrees() para obtener los grados de los nodos y getNeighbors() para obtener los vecinos o nodos adyacentes. Omitimos la parte destinada a la traza.
// https://en.wikipedia.org/wiki/Bron%E2%80%93Kerbosch_algorithm#With_pivoting
function getMaximalCliquesBronKerbosch({matrix=[]}) {
let result = [];
try {
function bronKerbosch(r=[], p=[], x=[], degrees=[], res=[]) {
if (p.length===0 && x.length===0) { // if P and X are both empty then
// report R as a maximal clique
let rr = r.toSorted((v, w) => v-w);
res.push(rr);
} else {
// choose a pivot vertex u in P ⋃ X
let px = [...p, ...x]; // P ⋃ X
px.sort((u,v) => degrees[v]-degrees[u]);
let u = px[0];
let nu = getNeighbors({matrix, index:u});
if (typeof nu==="string") throw new Error(nu);
let pu = []; // P \ N(u)
for (let item of p) {
if (!nu.includes(item)) pu.push(item);
}
for (let v of pu) { // for each vertex v in P \ N(u) do
let rr = [...r, v]; // R ⋃ {v}
let nv = getNeighbors({matrix, index:v});
if (typeof nv==="string") throw new Error(nv);
let pp = nv.filter(w => p.includes(w)); // P ⋂ N(v)
let xx = nv.filter(w => x.includes(w)); // X ⋂ N(v)
bronKerbosch(rr, pp, xx, degrees, res, level);
let k = p.findIndex(u => u===v);
if (k>-1) p.splice(k, 1); // P := P \ {v}
x = [...x, v]; // X := X ⋃ {v}
}
}
return res;
}
let n = matrix.length;
let directed = isGraphDirected({matrix});
if (typeof directed==="string") throw new Error(directed);
if (directed) {
for (let i=0; i<n; i++) {
for (let j=i; j<n; j++) {
if (matrix[i][j]>0 && matrix[j][i]===0) {
matrix[i][j] = 0;
} else if (matrix[i][j]===0 && matrix[j][i]>0) {
matrix[j][i] = 0;
}
}
}
}
let vertexs = Array.from({length: matrix.length}, (v,i) => i);
let degrees = getVertexDegrees({matrix});
if (typeof degrees==="string") throw new Error(degrees);
result = bronKerbosch([], vertexs, [], degrees);
} catch(e){result = e.message}
return result;
}Este algoritmo recursivo es un implementación del pseudo-código que aparece en la página mencionada del algoritmo de Bron-Kerbosch with pivoting para obtener los cliques maximales.
algorithm BronKerbosch2(R, P, X) is
if P and X are both empty then
report R as a maximal clique
choose a pivot vertex u in P ⋃ X
for each vertex v in P \ N(u) do
BronKerbosch2(R ⋃ {v}, P ⋂ N(v), X ⋂ N(v))
P := P \ {v}
X := X ⋃ {v}Aunque generalmente intento que los nombres de las variables sean significativos, no usando letras si es posible, en este caso he intentado respetar los nombres de variables del pseudo-código. En los comentarios del JavaScript se indica que parte de este pseudo-código se implementa.
Con respecto al JavaScript, solo anotar que hay operaciones de conjuntos como unión, intersección y diferenciación. Representamos un conjunto como array de JavaScript, así la operación A⋃B es tan simple como [...A, ...B] siempre que A y B sean disjuntos. Resulta que en el algoritmo aparece la unión P⋃X donde P y X siempre serán disjuntos, pues los vértices estarán en alguno de los tres conjuntos P, X o R, así que P⋃X se realiza con [...p, ...x]. Las uniones R⋃{v} o X⋃{v} también son entre conjuntos disjuntos, pues estamos agregando el vértice "v" a un conjunto que previamente no lo tenía, lo que se consigue con [...r, v] y [...x, v]. Para la intersección vemos que se trata de filtrar los vértices de N(v) que figuren en P o X, por lo que P⋂N(v) es lo mismo que hacer let nv.filter(w => p.includes(w)) y X⋂N(v) lo mismo que hacer nv.filter(w => x.includes(w)). La diferenciación P\{v} se consigue buscando el índice "k" de "v" en "p" y haciendo p.splice(k, 1).
En cualquier caso hice otra versión getMaximalCliquesBronKerboschSets() usando sólo conjuntos Set de JavaScript que puede descargar en este archivo en formato TXT.
Se observa que cuando el grafo es dirigido, antes de llamar por primera vez al recursivo eliminamos todas las aristas que no sean doblemente dirigidas, pues como ya explicamos nunca pueden formar parte de un subgrafo pues no sería completo, dado que con una arista "u🡒v" debe existir otra "v🡒u" para que sea completo. Esto lo hacemos con esta parte del código:
let n = matrix.length;
let directed = isGraphDirected({matrix});
if (typeof directed==="string") throw new Error(directed);
if (directed) {
for (let i=0; i<n; i++) {
for (let j=i; j<n; j++) {
if (matrix[i][j]>0 && matrix[j][i]===0) {
matrix[i][j] = 0;
} else if (matrix[i][j]===0 && matrix[j][i]>0) {
matrix[j][i] = 0;
}
}
}
}
El algoritmo es más fácil de implementar que de explicar. Por eso en la Figura vemos un grafo muy simple con los dos cliques maximales [[0,1],[0,2]] que nos servirá para tratar de explicar el funcionamiento. Con este JSON puede importar el ejemplo.
{"nodes":[
{"index":0,"parent":[{"index":-1}]},
{"index":1,"parent":[{"index":0}]},
{"index":2,"parent":[{"index":0}]}
],
"config":{
"algorithm":"Get maximal cliques (Bron-Kerbosch)",
"tracing":true,
"extendedTracing":true
}}Esta es la traza obtenida marcando también la opción trazado extendido, donde lo resaltado en azul es la traza básica sin extender. La primera llamada al recursivo es bronKerbosch(R, P, X) siendo R=[] el resultado donde al final de cada rama de llamadas podríamos tendremos un clique maximal, P=[0,1,2] contiene inicialmente los vértices del grafo y X=[] se usa para vértices que se excluirán de futuros cliques. Esta variable X es la más díficil de entender y se explicará más abajo.
bronKerbosch([], [0,1,2], [])
P ⋃ X ordered by increasing degree = [0,1,2]
u = 0
N(u) = [1,2] (Neighbors of u=0)
Loop in P \ N(u) = [0,1,2] \ [1,2] = [0]
# v = 0
N(v) = [1,2] (Neighbors of v=0)
R' := R ⋃ {v} = [] ⋃ [0] = [0]
P' := P ⋂ N(v) = [0,1,2] ⋂ [1,2] = [1,2]
X' := X ⋂ N(v) = [] ⋂ [1,2] = []
bronKerbosch([0], [1,2], [])
P ⋃ X ordered by increasing degree = [1,2]
u = 1
N(u) = [0] (Neighbors of u=1)
Loop in P \ N(u) = [1,2] \ [0] = [1,2]
# v = 1
N(v) = [0] (Neighbors of v=1)
R' := R ⋃ {v} = [0] ⋃ [1] = [0,1]
P' := P ⋂ N(v) = [1,2] ⋂ [0] = []
X' := X ⋂ N(v) = [] ⋂ [0] = []
bronKerbosch([0,1], [], []) ⇒ MAXIMAL: [0,1]
P := P \ {v} = [1,2] \ [1] = [2]
X := X ⋃ {v} = [] ⋃ [1] = [1]
# v = 2
N(v) = [0] (Neighbors of v=2)
R' := R ⋃ {v} = [0] ⋃ [2] = [0,2]
P' := P ⋂ N(v) = [2] ⋂ [0] = []
X' := X ⋂ N(v) = [1] ⋂ [0] = []
bronKerbosch([0,2], [], []) ⇒ MAXIMAL: [0,2]
P := P \ {v} = [2] \ [2] = []
X := X ⋃ {v} = [1] ⋃ [2] = [1,2]
P := P \ {v} = [0,1,2] \ [0] = [1,2]
X := X ⋃ {v} = [] ⋃ [0] = [0]Los conjuntos R, P y X son siempre disjuntos, pues inicialmente P contiene todos los vértices y en cada paso se van traspasando a R o X. Se encuentra el máximo clique con todos los vértices de R, algunos de los de P y ninguno de los de X. En cada llamada P y X son disjuntos, cuya unión son los vértices que formarán clique cuando se agreguen a R, es decir, P⋃X es el conjunto de vértices que son unidos para cada vértice de R. Cuando lleguemos a una llamada al recursivo con P y X vacíos entonces R contendrá un clique, que vemos en la traza por ejemplo en la primera devolución bronKerbosch([0,1], [], []) ⇒ MAXIMAL: [0,1].
En cada llamada se consideran los vértices de P⋃X y se busca el vértice de mayor grado "u", entonces solo consideramos los vértices de P\N(u) que no sean vecinos de "u". Esto es porque un maximal que podría ser encontrado chequeado los vecinos de "u" también podría ser encontrado chequeando "u" o sus no vecinos. Veamos como evoluciona el algoritmo.
Al principio tenemos R=[], P=[0,1,2], X=[] siendo P ⋃ X = [0,1,2] y u=0 el vértice con mayor grado que se selecciona, así que el bucle por el que iteraremos será P \ N(u) = [0,1,2] \ [1,2] = [0]. No es necesario considerar los vecinos de u=0, pues con cualquiera de ellos vamos a encontrar los mismos cliques que involucran a "0".
Dentro del bucle seleccionamos el primero y único elemento de P \ N(u) = [0] con v=0. Sus vecinos son N(0) = [1,2] con lo que creamos nuevas variables R' := R ⋃ {v} = [] ⋃ [0] = [0] agregado "0" a un posible clique R', actualizando los vértices con P' := P ⋂ N(v) = [0,1,2] ⋂ [1,2] = [1,2] y X' := X ⋂ N(v) = [] ⋂ [1,2] = [], con lo que restringuimos P y X a los vecinos de "v", tras lo cual hacemos la primera llamada bronKerbosch([0], [1,2], []). Esto quiere decir que si "0,1,2" pudieran formar clique entonces podrían ser "0,1" y/o "0,2", algo que vamos a descubrir en esa llamada bronKerbosch([0], [1,2], []).
En la vuelta de la llamada tenemos que u=1 es un vértice de mayor grado de P=[1,2], podría ser cualquiera de ellos pues ambos son del mismo grado, así que P \ N(1) = [1,2] \ [0] = [1,2], iterando sobre ellos tenemos:
v=1, N(1)=[0], R'=[0]⋃[1]=[0,1], P'=[1,2]⋂[0]=[], X'=[]⋂[0]=[]de tal forma que haciendo otra llamadabronKerbosch([0,1], [], [])ahora P y X son vacios y no hay más vertices que pudieran agregarse para formar un clique mayor, con lo que [0,1] es un maximal.v=2, N(2)=[0], R'=[0]⋃[2]=[0,2], P'=[1,2]⋂[0]=[], X'=[]⋂[0]=[]de tal forma que haciendo otra llamadabronKerbosch([0,2], [], [])ahora P y X son vacios y no hay más vertices que pudieran agregarse para formar un clique mayor, con lo que [0,2] es un maximal.
Con esto el algoritmo termina con los maximales [0,1], [0,2]. Vea que después del bucle quitamos v de P y se lo agregamos a X con objeto de buscar otros cliques que excluyan "v", pero como ya hemos finalizado no tendrá efecto alguno. Pero en caso de que el algoritmo continuase, esto quiere decir que si hubiera alguna llamada con X no vacio, entonces los vértices de R con P vacio y X no vacío no formarían clique, pues la condición es P y X vacíos. Lo que estamos haciendo es excluyendo en X los vértices que no formaran un clique futuro, pues ya fue considerado previamente como maximal en un clique de cierto tamaño y no puede estar en otro de tamaño superior pues entonces aquel no sería maximal.
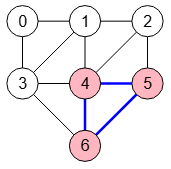
Veamos esto en esta traza de otro ejemplo de la Figura. Vemos en la traza que se forma el maximal [4,5,6], quedando posteriormente X'=[5], con lo que en la llamada bronKerbosch([4,6], [3], [5]) no puede ser maximal "4,5,6,3" dado que ya "4,5,6" fue encontrado maximal previamente y no puede haber otro clique de superior tamaño (vea en el grafo que "4,5,6,3" no es un clique pues no es un subgrafo completo pues falta la arista "3-5").
Loop in P \ N(u) = [2,6] \ [1,4,5] = [2,6]
...
bronKerbosch([4,5,6], [], []) ⇒ MAXIMAL: [4,5,6]
P := P \ {v} = [6] \ [6] = []
X := X ⋃ {v} = [2] \ [6] = [2,6]
P := P \ {v} = [2,3,5,6] \ [5] = [2,3,6]
X := X ⋃ {v} = [1] \ [5] = [1,5]
# v = 6
N(v) = [3,4,5] (Neighbors of v=6)
R' := R ⋃ {v} = [4] ⋃ [6] = [4,6]
P' := P ⋂ N(v) = [2,3,6] ⋂ [3,4,5] = [3]
X' := X ⋂ N(v) = [1,5] ⋂ [3,4,5] = [5]
bronKerbosch([4,6], [3], [5]) --------> "4,5,6,3" NO ES MAXIMAL
{"nodes":[
{"index":0,"parent":[{"index":-1}]},
{"index":3,"parent":[{"index":0,"lineTextOffset":-0.6},{"index":1,"lineTextOffset":-0.6}]},
{"index":1,"parent":[{"index":-1},{"index":0,"lineTextOffset":"0 -0.6"}]},
{"index":4,"parent":[{"index":1,"lineTextOffset":-0.6},{"index":3,"lineTextOffset":"0 0.6"},{"index":2,"lineTextOffset":0.6}]},
{"index":6,"parent":[{"index":4,"lineTextOffset":-0.6},{"index":3,"lineTextOffset":-0.6},{"index":5,"lineTextOffset":0.6}]},
{"index":2,"parent":[{"index":-1},{"index":1,"lineTextOffset":"0 -0.6"}]},
{"index":5,"parent":[{"index":2,"lineTextOffset":0.6},{"index":4,"lineTextOffset":"0 0.6"}]}
],
"config":{
"algorithm":"Get maximal cliques (Bron-Kerbosch)",
"pathColor":"blue",
"textColor":"red",
"tracing":true,
"extendedTracing":true
}}Obtener todos los anticliques en un grafo getAllAnticliques()
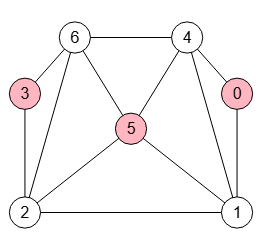
Un conjunto independiente o estable de nodos es un subconjunto de nodos de un grafo tal que no hay dos nodos adyacentes. A este subconjunto también se le denomina coclique o anticlique, término que vamos a usar y que luego entenderemos el motivo de ese nombre. El subconjunto siempre será de nodos, sin aristas, pues no pueden haber aristas entre esos nodos, por eso se le dice independiente.
Obtener todos los anticliques: [[0],[1],[2],[3],[4],[5],[6], [0,2],[0,3],[0,5],[0,6],[1,3], [1,6],[2,4],[3,4],[3,5], [0,3,5]]
En el grafo de la Figura se presenta el último anticlique obtenido de tamaño 3 compuesto por los nodos [0,3,5] observando que no hay aristas entre ellos. Los de tamaño 1 son todos los nodos y de tamaño 2 son aquellas parejas de nodos que no tienen arista entre ellos.
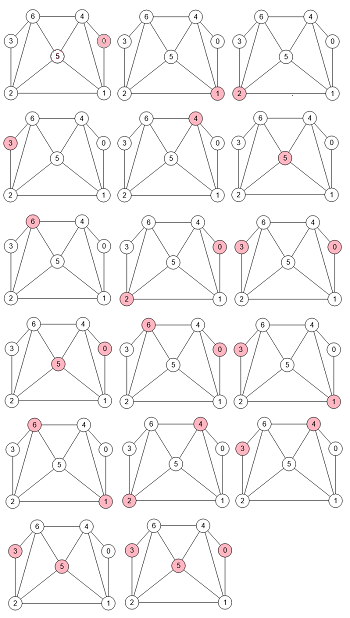
En la Figura vemos todos los 17 anticliques agrupados en una única imagen que se obtienen con el siguiente JSON y usando los botones que encontrará en la parte superior derecha del SVG en la aplicación.
{"nodes":[
{"index":0,"nodeOffset":"45 25","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"61.67 47.5","parent":[{"index":0}]},
{"index":2,"nodeOffset":"-23.33 22.5","parent":[{"index":1}]},
{"index":3,"nodeOffset":"-23.33 -50","parent":[{"index":2}]},
{"index":4,"nodeOffset":"8.33 -22.5","parent":[{"index":0},{"index":1}]},
{"index":5,"nodeOffset":"-14.17 -11","parent":[{"index":1},{"index":2},{"index":4}]},
{"index":6,"nodeOffset":"-36.67 -72.5","parent":[{"index":2},{"index":3},{"index":4},{"index":5}]}
],
"config":{
"algorithm":"Get all anticliques",
"findAll":true,
"ignoreSizeAnticlique12":false
}}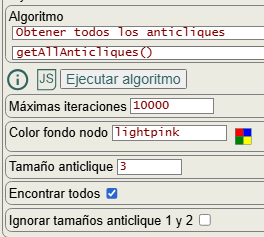
En la Figura vemos las opciones para obtener todos los anticliques. Con la opción tamaño anticlique seleccionamos entre 1 y el número de nodos del grafo. Con encontrar todos desmarcado nos devolverá todos los anticliques del tamaño especificado. Si está marcado buscará todos los anticliques de cualquier tamaño, a excepción de los tamaños 1 y 2 que se pueden ignorar como anticliques en la aplicación (pero no dejan de serlo) en caso de que la opción ignorar tamaños anticlique 1 y 2 esté marcada.
Las opción color fondo nodo no se pasa al algoritmo pues se aplica posteriormente sólo para resaltar los nodos del anticlique.
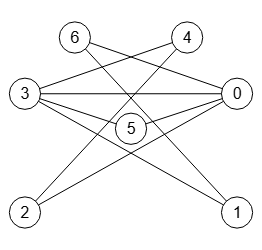
Un conjunto es un anticlique en un grafo sí y sólo sí es un clique en el grafo complemento. En la Figura vemos el grafo complemento, que se obtiene con la operación operateComplementGraph a partir del que vimos antes en la Figura, recordando que un grafo complemento (o complementario) es otro grafo con los mismos nodos donde las aristas son sólo aquellas que el grafo original no incluye.
{"error":"","matrix":
[[0,0,1,1,0,1,1],
[0,0,0,1,0,0,1],
[1,0,0,0,1,0,0],
[1,1,0,0,1,1,0],
[0,0,1,1,0,0,0],
[1,0,0,1,0,0,0],
[1,1,0,0,0,0,0]]}La operación devuelve una matriz de adyacencia, aunque posibilita posicionar los nodos en los mismos lugares.
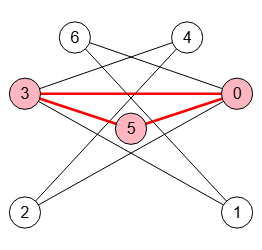
Obteniendo todos los cliques en el grafo complemento (sin ignorar los de tamaño 1 y 2) vemos que todos los resultados obtenidos a continuación son los mismos que vimos más arriba, presentándose en la Figura el último de mayor tamaño.
Obtener todos los cliques: [[0],[1],[2],[3],[4],[5],[6], [0,2],[0,3],[0,5],[0,6],[1,3], [1,6],[2,4],[3,4],[3,5], [0,3,5]]
{"nodes":[
{"index":0,"nodeOffset":"61.67 25","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"28.33 72.5","parent":[{"index":-1}]},
{"index":2,"nodeOffset":"-10 47.5","parent":[{"index":0}]},
{"index":3,"nodeOffset":"-30","parent":[{"index":0},{"index":1}]},
{"index":4,"nodeOffset":"25 -47.5","parent":[{"index":2},{"index":3}]},
{"index":5,"nodeOffset":"-7.5 14","parent":[{"index":0},{"index":3}]},
{"index":6,"nodeOffset":"-50 -22.5","parent":[{"index":0},{"index":1}]}
],
"config":{
"algorithm":"Get all cliques",
"findAll":true,
"ignoreSizeClique12":false
}}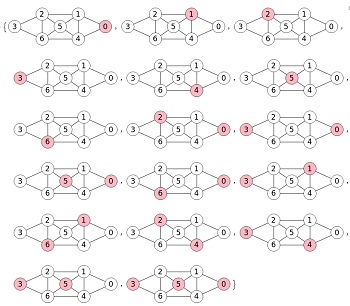
En la Figura vemos todos los anticliques obtenidos en Wolfram, los mismos 17 de nuestra aplicación. Si desmarcamos la línea s = Select[c, IndependentVertexSetQ[g, #]&] obtenemos los mismos subconjuntos, aunque con índices iniciándose desde 1 como es usual en Wolfram: {{1},{2},{3},{4},{5},{6},{7},{1,3},{1,4},{1,6},{1,7},{2,4},{2,7},{3,5},{4,5},{4,6},{1,4,6}}
El proceso es obtener todos los vértices con v = VertexList[g] y todas sus combinaciones c = Subsets[v, {1,Infinity}] del tamaño especificado, todos en este caso, para luego filtrar aquellos que formen un conjunto indendendiente de vértices con s = Select[c, IndependentVertexSetQ[g, #]&]
Wolfram dispone de la función FindIndependentVertexSet, pero al igual que pasaba con FindClique sólo encuentra máximos y maximales conjuntos independientes (como veremos después), pues define conjunto independiente de vértices como un conjunto maximal que no tiene aristas incidentes. En cambio para nosotros no necesariamente han de ser maximales. Para encontrarlos todos en Wolfram no queda más remedio que usar las combinaciones y comprobar una a una que es un conjunto independiente con IndependentVertexSetQ
g = AdjacencyGraph[{{0,1,0,0,1,0,0},{1,0,1,0,1,1,0},{0,1,0,1,0,1,1},{0,0,1,0,0,0,1},{1,1,0,0,0,1,1},{0,1,1,0,1,0,1},{0,0,1,1,1,1,0}}, ImageSize -> 250,
VertexSize -> {"Scaled", 0.13}, VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center], 3 -> Placed[2,Center], 4 -> Placed[3,Center],
5 -> Placed[4,Center], 6 -> Placed[5,Center], 7 -> Placed[6,Center]}, VertexLabelStyle -> Directive[Black,17.5], EdgeLabelStyle -> Directive[Black,17.5,Bold],
VertexStyle -> White, EdgeStyle -> {{Black,Thickness[0.005]}}];
v = VertexList[g];
c = Subsets[v, {1,Infinity}];
s = Select[c, IndependentVertexSetQ[g, #]&];
Table[HighlightGraph[g,{Style[i, RGBColor["lightpink"]]}], {i,s}]El JavaScript para ejecutar getAllAnticliques() es el siguiente. Usa operateComplementGraph() para obtener el grafo complemento, sobre el que aplicamos getAllCliques() para obtener todos los cliques de ese grafo que serán los anticliques del grafo original.
function getAllAnticliques({matrix=[], sizeAnticlique=3, findAll=false, ignoreSizeAnticlique12=true}) {
let result = [];
try {
let minSize = findAll && ignoreSizeAnticlique12 ? 3 : 1;
let complement = operateComplementGraph({matrix});
if (complement.error) throw new Error(complement.error);
let n = complement.matrix.length;
sizeAnticlique = Math.max(minSize, Math.min(sizeAnticlique, n));
let cliques = getAllCliques({matrix:complement.matrix, sizeClique:sizeAnticlique, findAll, ignoreSizeClique12:ignoreSizeAnticlique12});
if (typeof cliques==="string") throw new Error(cliques);
if (cliques.hasOwnProperty("warnings")) result.warnings = cliques.warnings;
result.push(...cliques);
} catch(e){result = e.message}
return result;
}Obtener anticliques máximos en un grafo getMaximumAnticliques()
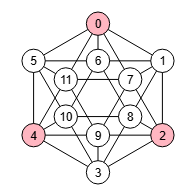
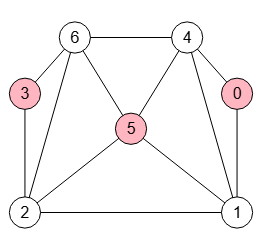
Un anticlique máximo es un anticlique de tamaño mayor posible. En la Figura vemos un anticlique máximo del grafo icosaédrico, obteniéndose 20 anticliques de tamaño 3, presentándose en la Figura el primero de ellos
El número de indendencia de un grafo G se denota como α(G) y viene a ser el tamaño del anticlique máximo, o equivalentemente, el máximo conjunto independiente. Así que para nuestro ejemplo α(G) = 3
A continuación vemos el resultado que devuelve la aplicación con los 20 anticliques de tamaño máximo 3, pudiendo acceder visualmente al resto con los botones de navegación que encontrará en la parte superior derecha del SVG en la aplicación.
Obtener máximos anticliques: [[0,2,4],[0,2,10],[0,4,8],[0,8,9],[0,9,10],[1,3,5],[1,3,11],[1,5,9],[1,9,10],[1,10,11], [2,4,6],[2,6,11],[2,10,11],[3,5,7],[3,6,7],[3,6,11],[4,6,7],[4,7,8],[5,7,8],[5,8,9]]
Con este JSON puede importar el ejemplo.
{"nodes":[
{"index":0,"nodeOffset":"2.5 0.17","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"70.33 -4.91","parent":[{"index":0}]},
{"index":2,"nodeOffset":"53.67 9.91","parent":[{"index":1}]},
{"index":3,"nodeOffset":"19.17 4.83","parent":[{"index":2}]},
{"index":4,"nodeOffset":"-15.33 -40.09","parent":[{"index":3}]},
{"index":5,"nodeOffset":"-15.33 -4.91","parent":[{"index":0},{"index":4}]},
{"index":6,"nodeOffset":"2.5 -4.91","parent":[{"index":0},{"index":1},{"index":5}]},
{"index":7,"nodeOffset":"3.08 5.05","parent":[{"index":0},{"index":1},{"index":2}]},
{"index":8,"nodeOffset":"3.08 -0.05","parent":[{"index":1},{"index":2},{"index":3},{"index":6}]},
{"index":9,"nodeOffset":"-14.17 -15.09","parent":[{"index":2},{"index":3},{"index":4},{"index":7}]},
{"index":10,"nodeOffset":"-31.42 -50.05","parent":[{"index":3},{"index":4},{"index":5},{"index":6},{"index":8}]},
{"index":11,"nodeOffset":"-48.08 5.05","parent":[{"index":0},{"index":4},{"index":5},{"index":7},{"index":9}]}
],
"config":{
"lineHeight":18.75,
"algorithm":"Get maximum anticliques",
"ignoreSizeAnticlique12":false
}}
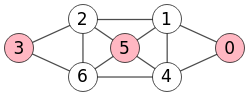
Para el ejemplo de la Figura donde obteníamos todos los anticliques [[0],[1],[2],[3],[4],[5],[6], [0,2],[0,3],[0,5],[0,6],[1,3],[1,6],[2,4],[3,4],[3,5],[0,3,5]] el anticliqué máximo es el último [[0,3,5]]
{"nodes":[
{"index":0,"nodeOffset":"45 25","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"61.67 47.5","parent":[{"index":0}]},
{"index":2,"nodeOffset":"-23.33 22.5","parent":[{"index":1}]},
{"index":3,"nodeOffset":"-23.33 -50","parent":[{"index":2}]},
{"index":4,"nodeOffset":"8.33 -22.5","parent":[{"index":0},{"index":1}]},
{"index":5,"nodeOffset":"-14.17 -11","parent":[{"index":1},{"index":2},{"index":4}]},
{"index":6,"nodeOffset":"-36.67 -72.5","parent":[{"index":2},{"index":3},{"index":4},{"index":5}]}
],
"config":{
"algorithm":"Get maximum anticliques",
"ignoreSizeAnticlique12":false
}}
En la Figura puede ver los anticliques máximos en Wolfram, uno en este caso como en nuestro ejemplo. Usa FindIndependentVertexSet para obtener los conjuntos independientes máximos de vértices que, como hemos visto, es equivalente a los anticliques máximos.
g = AdjacencyGraph[{{0,1,0,0,1,0,0},{1,0,1,0,1,1,0},{0,1,0,1,0,1,1},{0,0,1,0,0,0,1},{1,1,0,0,0,1,1},{0,1,1,0,1,0,1},{0,0,1,1,1,1,0}}, ImageSize -> 250,
VertexSize -> {"Scaled", 0.13}, VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center], 3 -> Placed[2,Center], 4 -> Placed[3,Center],
5 -> Placed[4,Center], 6 -> Placed[5,Center], 7 -> Placed[6,Center]}, VertexLabelStyle -> Directive[Black,17.5], EdgeLabelStyle -> Directive[Black,17.5,Bold],
VertexStyle -> White, EdgeStyle -> {{Black,Thickness[0.005]}}];
s = FindIndependentVertexSet[g, Length /@ FindIndependentVertexSet[g], All];
Table[HighlightGraph[g,{Style[i, RGBColor["lightpink"]]}], {i,s}]La expresión Length /@ FindIndependentVertexSet[g] es para aplicar Length con Map y obtener el tamaño del conjunto. Como FindIndependentVertexSet[g] sin más argumentos encuentra un único conjunto máximo, con Length /@ FindIndependentVertexSet[g] nos devolverá el tamaño {3} de ese conjunto, valor que trasladamos a FindIndependentVertexSet[g, 3, All] para encontrar todos los de tamaño 3. Así que la sentencia anterior con el uso de /@ equivale estas dos:
m = Map[Length, FindIndependentVertexSet[g]]
s = FindIndependentVertexSet[g, m, All];
Wolfram expone que se puede aplicar FindIndependentVertexSet de esta forma para obtener los conjuntos independientes de vértices:
- Conjuntos independientes de vértices máximos
FindIndependentVertexSet[g]encuentra un único conjunto máximo de un grafo "g"FindIndependentVertexSet[g, Length/@FindIndependentVertexSet[g], s]encuentra como mucho "s" conjuntos máximosFindIndependentVertexSet[g, Length/@FindIndependentVertexSet[g], All]encuentra todos los conjuntos máximos
- Conjuntos independientes de vértices maximales
FindIndependentVertexSet[g, Infinity]encuentra un único conjunto maximal de un grafo "g"FindIndependentVertexSet[g, Infinity, s]encuentra como mucho "s" conjuntos maximalesFindIndependentVertexSet[g, Infinity, All]encuentra todos los conjuntos maximales
El JavaScript para ejecutar getMaximumAnticliques(). Usa operateComplementGraph() para obtener el grafo complemento, sobre el que aplicamos getAllCliques() iterando desde el tamaño del total de nodos del grafo hasta 1, de tal forma que cuando encontremos el primer tamaño que forma clique en el grafo complemento lo devolvemos y finalizamos, siendo este clique el anticlique del grafo original.
function getMaximumAnticliques({matrix=[], ignoreSizeAnticlique12=true}) {
let result = [];
try {
let minSize = ignoreSizeAnticlique12 ? 3 : 1;
let complement = operateComplementGraph({matrix});
if (complement.error) throw new Error(complement.error);
let n = complement.matrix.length;
for (let j=n; j>=minSize; j--) {
let cliques = getAllCliques({matrix:complement.matrix, sizeClique:j, findAll:false});
if (typeof cliques==="string") throw new Error(cliques);
if (cliques.hasOwnProperty("warnings")) {
result.warnings = cliques.warnings;
break;
}
if (cliques.length>0) {
result.push(...cliques);
break;
}
}
} catch(e){result = e.message}
return result;
}Obtener anticliques maximales en un grafo getMaximalAnticliques()
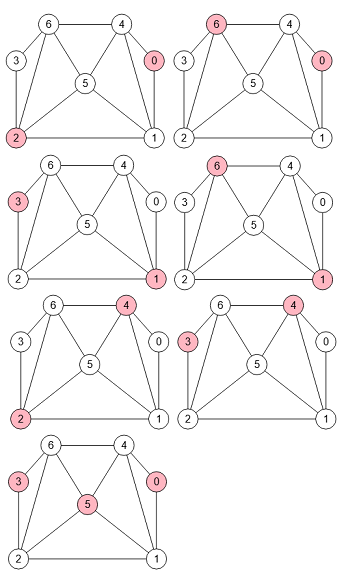
Un anticlique maximal es un anticlique que no forma parte de otro de mayor tamaño. En la Figura vemos todos los anticliques maximales del grafo, obteniéndose el resultado [[0,2],[0,6],[1,3],[1,6],[2,4],[3,4],[0,3,5]].
Si recordamos todos los anticliques del mismo grafo que vimos en la Figura, vemos que obteníamos [[0],[1],[2],[3],[4],[5],[6], [0,2],[0,3],[0,5],[0,6],[1,3], [1,6],[2,4],[3,4],[3,5], [0,3,5]]. De estos sólo los resaltados en azul son maximales, puesto que agregando más nodos no obtenemos un anticlique de tamaño superior. Así los de tamaño 1 no son maximales pues podemos agregarle otro nodo para hacer un maximal de tamaño 2. Ni son maximales [0,3], [0,5] y [3,5] pues podemos agregarle el faltante para formar [0,3,5] de tamaño superior.
{"nodes":[
{"index":0,"nodeOffset":"45 25","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"61.67 47.5","parent":[{"index":0}]},
{"index":2,"nodeOffset":"-23.33 22.5","parent":[{"index":1}]},
{"index":3,"nodeOffset":"-23.33 -50","parent":[{"index":2}]},
{"index":4,"nodeOffset":"8.33 -22.5","parent":[{"index":0},{"index":1}]},
{"index":5,"nodeOffset":"-14.17 -11","parent":[{"index":1},{"index":2},{"index":4}]},
{"index":6,"nodeOffset":"-36.67 -72.5","parent":[{"index":2},{"index":3},{"index":4},{"index":5}]}
],
"config":{
"algorithm":"Get maximal anticliques"
}}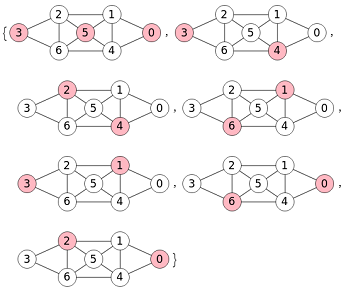
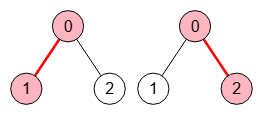
En la Figura puede ver los anticliques maximales en Wolfram, los mismo que en nuestro ejemplo. Usa FindIndependentVertexSet para obtener los conjuntos independientes maximales de vértices que es equivalente a los anticliques maximales.
g = AdjacencyGraph[{{0,1,0,0,1,0,0},{1,0,1,0,1,1,0},{0,1,0,1,0,1,1},{0,0,1,0,0,0,1},{1,1,0,0,0,1,1},{0,1,1,0,1,0,1},{0,0,1,1,1,1,0}}, ImageSize -> 250,
VertexSize -> {"Scaled", 0.13}, VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center], 3 -> Placed[2,Center], 4 -> Placed[3,Center],
5 -> Placed[4,Center], 6 -> Placed[5,Center], 7 -> Placed[6,Center]}, VertexLabelStyle -> Directive[Black,17.5], EdgeLabelStyle -> Directive[Black,17.5,Bold],
VertexStyle -> White, EdgeStyle -> {{Black,Thickness[0.005]}}];
s = FindIndependentVertexSet[g, Infinity, All];
Table[HighlightGraph[g,{Style[i, RGBColor["lightpink"]]}], {i,s}]Recordamos otra vez que Wolfram expone que se puede aplicar FindIndependentVertexSet de esta forma para obtener los conjuntos independientes de vértices:
- Conjuntos independientes de vértices máximos
FindIndependentVertexSet[g]encuentra un único conjunto máximo de un grafo "g"FindIndependentVertexSet[g, Length/@FindIndependentVertexSet[g], s]encuentra como mucho "s" conjuntos máximosFindIndependentVertexSet[g, Length/@FindIndependentVertexSet[g], All]encuentra todos los conjuntos máximos
- Conjuntos independientes de vértices maximales
FindIndependentVertexSet[g, Infinity]encuentra un único conjunto maximal de un grafo "g"FindIndependentVertexSet[g, Infinity, s]encuentra como mucho "s" conjuntos maximalesFindIndependentVertexSet[g, Infinity, All]encuentra todos los conjuntos maximales
El JavaScript para ejecutar getMaximalAnticliques(). Usa operateComplementGraph() para obtener el grafo complemento, sobre el que aplicamos getMaximalCliquesBronKerbosch() para obtener el clique maximal del complemento que será al anticlique maximal del grafo original.
function getMaximalAnticliques({matrix=[]}) {
let result = [];
try {
let complement = operateComplementGraph({matrix});
if (complement.error) throw new Error(complement.error);
let maximal = getMaximalCliquesBronKerbosch({matrix: complement.matrix});
if (typeof maximal==="string") throw new Error(maximal);
result = maximal.cliques.toSorted((u,v) => u.length-v.length);
} catch(e){result = e.message}
return result;
}