Algoritmo de Dijkstra: Caminos mínimos
Caminos mínimos en un grafo dirigido
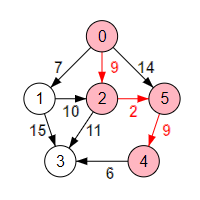
En el problema de los caminos mínimos tenemos un grafo dirigido donde hay un nodo raíz y cada arista tiene una longitud, pudiendo recorrerse el camino desde el nodo raíz a cualquier nodo del grafo. Ese recorrido se hará siguiendo la dirección de las aristas. Se trata de obtener esos caminos a cada nodo cuya longitud es mínima.
La Figura resalta un camino entre el nodo 0 y el 4. Pasa por los nodos 0 → 2 → 5 → 4 con longitud 20, siendo éste el mínimo. Los otros dos caminos posibles son 0 → 5 → 4 con longitud 23 y 0 → 1 → 2 → 5 → 4 con longitud 28, ambos con longitud superior.
Algoritmo de Dijkstra para resolver caminos mínimos
getShortestPathDijkstra(), como el que se expone aquí con algunas mejoras.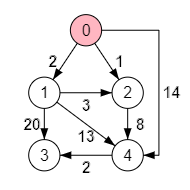
El algoritmo de Dijkstra es un algoritmo voraz que resuelve el problema de los caminos mínimos. Para explicarlo tomaremos el primer ejemplo que puede ejecutar en el interactivo que veremos más abajo. Partimos del grafo dirigido que se muestra en la Figura.
En ese grafo vemos el nodo raíz resaltado significando que siempre se selecciona ese nodo como inicio de todos los caminos posibles a cualquier otro nodo. En la definición del grafo usamos la estructura que ya vimos en temas anteriores. Se trata de un array de nodos, donde cada nodo es un objeto con las propiedades obligatorias index y parent. El índice siempre empezará en cero. La propiedad parent es un array con las relaciones con otros nodos. Es decir, cada entrada de este array es una arista a otro nodo.
[
{"index":0,"parent":-1},
{"index":1,"parent":[
{"index":0,"value":2,"markerStart":"arrow"}
]},
{"index":2,"parent":[
{"index":0,"value":1,"markerStart":"arrow"},
{"index":1,"value":3,"markerStart":"arrow"}
]},
{"index":3,"parent":[
{"index":1,"value":20,"markerStart":"arrow"},
{"index":4,"value":2,"markerStart":"arrow"}
]},
{"index":4,"parent":[
{"index":1,"value":13,"markerStart":"arrow"},
{"index":2,"value":8,"markerStart":"arrow"},
{"index":0,"value":14,"markerStart":"arrow"}
]}
]En la estructura anterior verá que el nodo cero apunta a -1 significando que es el nodo raíz. Las relaciones parent necesitan agregarle la propiedad markerStart o markerEnd con valor arrow. Si por ejemplo el nodo 1 tiene una relación parent que apunta al nodo 0 hemos de cambiar el sentido de la relación con markerStart: arrow.
Por otro lado si el nodo 2 tiene una relación parent que apunta al nodo 1 usando markerStart, podemos trasladar esa relación al nodo 1 que apunte al nodo 2 usando una relación markerEnd, como se observa a continuación:
...
{"index":1,"parent":[
{"index":0,"value":2,"markerStart":"arrow"},
{"index":2,"value":3,"markerEnd":"arrow"}
]},
{"index":2,"parent":[
{"index":0,"value":1,"markerStart":"arrow"}
]},
...Esta forma de estructurar el grafo nos permitirá usar la herramienta grafos con SVG para generar los grafos con facilidad.
Para resolver el problema necesitamos un array de dimensión n × n que contiene las longitudes de todas las aristas. Si i, j son los índices de dos nodos con una arista en la dirección i → j, una entrada en este array longitudes[i][j] nos dará la longitud si existe esa arista. Si no existe nos dará ∞. Como el grafo es dirigido, una arista o bien no existe o si existe lo hace en una única dirección. Para el ejemplo de la Figura obtenemos el siguiente array:
| i ↓ | j → | ||||
|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | |
| 0 | ∞ | 2 | 1 | ∞ | 14 |
| 1 | ∞ | ∞ | 3 | 20 | 13 |
| 2 | ∞ | ∞ | ∞ | ∞ | 8 |
| 3 | ∞ | ∞ | ∞ | ∞ | ∞ |
| 4 | ∞ | ∞ | ∞ | 2 | ∞ |
Para obtener este array usaremos la siguiente función que itera por la estructura del grafo observando la propiedad markerStart o markerEnd para descubrir la dirección de la arista:
function obtenerLongitudes(nodes=[]){
let n = nodes.length;
let longitudes = Array.from({length:n}, () =>
Array.from({length:n}, () => Infinity));
for (let node of nodes){
if (Array.isArray(node.parent)){
for (let link of node.parent){
if (typeof link==="object"){
if (link.markerEnd==="arrow") {
longitudes[node.index][link.index] = link.value;
} else if (link.markerStart==="arrow") {
longitudes[link.index][node.index] = link.value;
}
}
}
}
}
return longitudes;
}Con la función anterior el algoritmo de Dijkstra es el siguiente:
function dijkstra(nodes=[]){
let longitudes = obtenerLongitudes(nodes);
let caminos = nodes.map((v,i) => longitudes[0][i]);
let candidatos = nodes.map((v,i) => v.index).filter(v => v>0);
let punteros = Array.from({length: nodes.length}, () => 0);
//Es suficiente con candidatos.length>1
while (candidatos.length>0) {
let k, min = Infinity;
for (let j of candidatos){
if (caminos[j]<min){
min = caminos[j];
k = j;
}
}
candidatos = candidatos.filter(v => v!==k);
for (let j of candidatos) {
if (caminos[j] > caminos[k] + longitudes[k][j]){
caminos[j] = caminos[k] + longitudes[k][j];
punteros[j] = k;
}
}
}
return {caminos, punteros};
}A continuación se presenta el ejemplo interactivo. Luego explicaremos paso a paso el primer ejemplo.
Ejemplo: Algoritmo de Dijkstra
dijkstra(grafo): 
Antes de iterar por el bucle voraz iniciamos el array de longitudes de aristas tal como comentamos antes. Necesitamos también un array caminos que contendrá la longitud de los caminos especiales. Un camino desde el nodo raíz (índice cero) hasta cualquier otro nodo es especial si todos los nodos del camino ya han sido seleccionados. Inicialmente este array contiene las longitudes del nodo raíz hasta el resto de nodos, que se obtiene de la fila i=0 del array de longitudes.
Un siguiente array necesario es candidatos. Contiene los índices de todos los nodos que aún no se han seleccionado. No contiene el nodo raíz, pues recordemos que antes de iniciar el bucle voraz seleccionamos el nodo cero, como se muestra en la Figura.
El array caminos nos dará al final la longitud del camino mínimo desde el raíz a cada nodo. Por ejemplo, al final obtendremos caminos = [∞, 2, 1, 11, 9]. Por ejemplo, caminos[3] = 11 significando que la distancia mínima entre nodos 0 → 3 es 11.
Para saber los nodos que atraviesa ese camino mínimo 0 → 3 usaremos el array punteros. Obtendremos al final punteros = [0, 0, 0, 4, 2]. Desferenciando obtenemos punteros[3] = 4 ⇒ punteros[4] = 2 ⇒ punteros[2] = 0, por lo que el camino mínimo 0 → 3 de longitud 11 pasa por los nodos 0 → 2 → 4 → 3.
La situación inicial de todos los arrays antes de empezar el bucle voraz es la siguiente:
longitudes =
0 1 2 3 4
0 ∞ 2 1 ∞ 14
1 ∞ ∞ 3 20 13
2 ∞ ∞ ∞ ∞ 8
3 ∞ ∞ ∞ ∞ ∞
4 ∞ ∞ ∞ 2 ∞
caminos = [∞, 2, 1, ∞, 14]
candidatos = [1, 2, 3, 4]
punteros = [0, 0, 0, 0, 0]Veamos ahora las iteraciones del bucle voraz, tantas como candidatos existan.
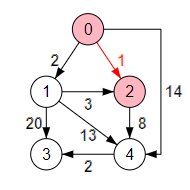
Primera iteración. El array caminos = [∞, 2, 1, ∞, 14] contiene las distancias al nodo raíz. Con el bucle siguiente localizamos el mínimo valor:
let k, min = Infinity;
for (let j of candidatos){
if (caminos[j]<min){
min = caminos[j];
k = j;
}
}Obtenemos el índice del nodo k=2 que está más cerca del nodo raíz, con longitud 1. El array candidatos contenía [1, 2, 3, 4]. Quitamos ese nodo k=2 mediante la sentencia candidatos.filter(v => v!==k), quedando candidatos = [1, 3, 4].
Usamos el método de Array filter puesto que hay que tener en cuenta que el array candidatos no tiene por que seguir el orden [1,2,3,4]. Podría ser [2,1,3,4] como en el "Ejemplo 2" del ejemplo interactivo. Dependerá de como se estructuran los nodos en el grafo. Además la selección no sigue necesariamente el orden del array, como es el caso de esta primera iteración que seleccionó el nodo k=2. Así que la iteración del bucle voraz se consigue quitando índices del array de candidatos a medida que se vayan seleccionando.
Terminamos esta primera iteración actualizando los arrays caminos y punteros con esta parte del código:
for (let j of candidatos) {
if (caminos[j] > caminos[k] + longitudes[k][j]){
caminos[j] = caminos[k] + longitudes[k][j];
punteros[j] = k;
}
}Iteramos por los candidatos no seleccionados que ahora son [1, 3, 4] para descubrir si la distancia anterior desde el nodo raíz hasta un candidato es mayor que la distancia al nodo seleccionado k=2 más la longitud entre los nodos k y j. En ese caso actualizamos caminos[j] a la menor distancia y referenciamos punteros[j] = k. Veamos con detalle este bucle:
caminos = [∞, 2, 1, ∞, 14] candidatos = [1, 3, 4] punteros = [0, 0, 0, 0, 0] k=2 longitudes[2] = [∞, ∞, ∞, ∞, 8] Bucle: j caminos[j] > caminos[2]+longitudes[2][j] ----------------------------------------------- 1 2 > 1+∞ = ∞ ⇒ falso 2 1 > 1+∞ = ∞ ⇒ falso 3 ∞ > 1+∞ = ∞ ⇒ falso 4 14 > 1+8 = 9 ⇒ cierto
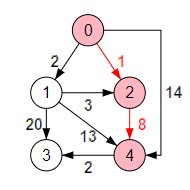
Observe en la Figura como el único nodo que está más cerca del seleccionado k=2 es el nodo 4, reflejándose esto en el bucle anterior. Tras eso los tres arrays quedan preparados para la siguiente iteración:
i=1 k=2 caminos = [∞, 2, 1, ∞, 9] candidatos = [1, 3, 4] punteros = [0, 0, 0, 0, 2]
Los resaltes amarillos son los cambios con respecto a la situación anterior. Los resaltes verdes son las posiciones de los nodos ya seleccionados, en este caso el nodo k=2. Estos ya no se consideran en las siguientes iteraciones. Recuerde que las posiciones cero de los arrays caminos y punteros no se tienen en cuenta.
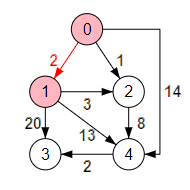
Segunda iteración. Entre los nodos candidatos [1, 3, 4] el más cercano en caminos es el nodo k=1 que está a una distancia 2. Seleccionamos este nodo y actualizamos arrays:
i=2 k=1 caminos = [∞, 2, 1, 22, 9] candidatos = [3, 4] punteros = [0, 0, 0, 1, 2]
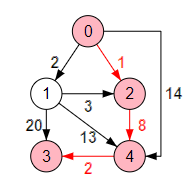
Tercera iteración. Entre los nodos candidatos [3, 4] el más cercano en caminos es el nodo k=4 que está a una distancia 9. Seleccionamos este nodo y actualizamos arrays:
i=3 k=4 caminos = [∞, 2, 1, 11, 9] candidatos = [3] punteros = [0, 0, 0, 4, 2]
Cuarta iteración. Sólo queda un candidato [3]. Realmente este último paso no es ni siquiera necesario ejecutarlo, pues la situación con respecto a la anterior no cambia:
i=4 k=3 caminos = [∞, 2, 1, 11, 9] candidatos = [] punteros = [0, 0, 0, 4, 2]
Es así puesto que la distancia mínima de un nodo y su puntero (el nodo 3 en este caso) ya se actualizó en una iteración anterior cuando se seleccionado otro nodo antes (el 4). En el código del algoritmo pusimos una línea de comentario en la cabecera del bucle voraz para anotar que sólo es necesario iterar por uno menos de todos los candidatos, con lo que nos ahorraríamos una iteración:
...
//Es suficiente con candidatos.length>1
while (candidatos.length>0) {
...El coste del algoritmo de Dijkstra
Analizando el algoritmo que expusimos en el apartado anterior, inicialmente tenemos que obtener las longitudes entre todas las aristas. Tiene un coste O(n3), pues hay que hacer el mismo recorrido que vimos para la obtención de las aristas en el algoritmo de Kruskal del tema anterior.
Supongamos que nos dieran ese array de longitudes ya formado en la entrada del algoritmo y, por tanto, no consideramos ese coste. En el código vemos que tenemos que crear los arrays de caminos, candidatos y punteros, todos con longitud n. El bucle voraz while y los dos bucles for interiores tienen la longitud del array de candidatos, es decir, n. Por lo tanto el coste final será O(n2).