Programación dinámica
La programación dinámica
Dividir un problema en subproblemas más sencillos para poder resolverlos y luego combinar sus soluciones para obtener la solución general, es una técnica que usamos para resolver problemas, como por ejemplo en los recursivos. Pero a veces los subproblemas se solapan o se calcula lo mismo en varios subproblemas, restando eficiencia a la ejecución de la solución final. Un ejemplo de esto que veremos después es la ejecución de la función recursiva de Fibonacci f(n) = f(n-1) + f(n-2).
Otras veces los algoritmos de optimización como los voraces no logran el resultado final óptimo para algunos conjuntos de datos. Veremos el caso del problema de devolver cambio para un conjunto de monedas como {1, 3, 5, 6}, donde el algoritmo voraz no consigue un resultado óptimo para devolver algunos valores. En la Figura puede ver la tabla de resultados intermedios para el problema de devolver cambio. Las posiciones marcadas sirven para resolver el número de monedas que hay que devolver para un cambio con valor 8.
La programación dinámica intenta resolver esta falta de eficiencia o eficacia planteándose como una técnica para evitar calcular lo mismo varias veces, siempre de una forma óptima. Usa una tabla de resultados intermedios mientras resolvemos los subproblemas, resultados óptimos que luego se utilizarán posteriormente para alcanzar la solución óptima final.
Para resolverlo, la programación dinámica se basa en el principio de optimalidad que dice que en una secuencia de decisiones óptimas toda subsecuencia también es óptima. Esto es clave para abordar problemas de optimización, planteándose una secuencia de decisiones óptimas que nos lleven a alcanzar el resultado final óptimo. Sin embargo no podemos ignorar que todos los problemas de optimización no obedecen a este principio, por lo que hemos de tener claro que se cumple cuando abordemos con esta técnica un problema.
Fibonacci: Problemas superpuestos
En el tema de recursivos vimos el de Fibonacci, que se define como f(n) = f(n-1) + f(n-2). Su implementación en JavaScript da lugar al siguiente algoritmo:
function fibonacci1(n){
if (n<2){
return n;
} else {
return fibonacci1(n-1) + fibonacci1(n-2);
}
}Vimos en ese tema que tiene un coste exponencial O(Φn), siendo Φ = (1+5½)/2 la razón áurea. Es un algoritmo costoso porque se realizan repetidas veces los cálculos. Por ejemplo, para T(5) se calcula 1 vez T(5), 1 vez T(4), 2 veces T(3) y 3 veces T(2). Esto suma 7 operaciones:
T(5) = T(4) + T(3) + 1
T(4) = T(3) + T(2) + 1
T(3) = T(2) + T(1) + 1
T(2) = T(1) + T(0) + 1
T(2) = T(1) + T(0) + 1
T(3) = T(2) + T(1) + 1
T(2) = T(1) + T(0) + 1
Este efecto es lo que se conoce como subproblemas superpuestos. Siempre que se detecten en la resolución de un problema hay que tratar de eliminarlos pues encarecen enormemente el coste. Vimos también que era posible obtener un Fibonacci con coste lineal, presentándose las siguientes versiones iterativa y recursiva:
//Iterativo
function fibonacci2(n){
let i = 1, j = 0;
for (let k=1; k<=n; k++){
[i, j] = [j, i+j];
}
return j;
}
//Recursivo
function fibonacci3(n, ri=0, rj=1){
if (n<1){
return ri;
} else if (n<2) {
return rj;
} else {
let p = n-1;
[ri, rj] = [rj, ri+rj];
return fibonacci3(p, ri, rj);
}
}Hemos reducido el coste a O(n). Esto es de hecho una aplicación de la programación dinámica. En cada paso vamos almacenando los valores obtenidos [i, j] = [j, i+j], usándose la suma i+j como valor ya calculado para la siguiente iteración. Esa operación i+j sólo se calcula una vez en la iteración i-ésima.
| i↓ | Valor j → | ||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 0 | 0 | ||||||||
| 1 | 0 | 1 | |||||||
| 2 | 0 | 1 | 1 | ||||||
| 3 | 0 | 1 | 1 | 2 | |||||
| 4 | 0 | 1 | 1 | 2 | 3 | ||||
| 5 | 0 | 1 | 1 | 2 | 3 | 5 | |||
| 6 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | ||
| 7 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | |
| 8 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 |
Los valores que vamos almacenando en cada iteración podemos denominarlos como resultados intermedios. De hecho podemos pensar que está implícito la existencia de una tabla de resultados intermedios como la de la Figura. En esa tabla la dirección horizontal j es el valor sobre el que se aplica el problema, Fibonacci(j) para nuestro caso. Mientras que la dirección vertical i son las iteraciones. Empezamos en el punto (0, 0) y vamos construyendo la tabla T con la propia función de Fibonacci T[i][j] = T[i-1][j-1] + T[i-2][j-2], con la salvedad que los valores para i=0 e i=1 deben rellenarse previamente para evitar la inexistencia de posiciones anteriores.
De hecho sólo tendríamos que rellenar la diagonal en color azul, pues el resto de diagonales contienen la misma información desplazada. Así la tabla de resultados sería un simple Array de dimensión igual que el máximo valor a calcular y sus posiciones contendrían la sucesión de Fibonacci 0, 1, 1, 2, 3, 5, 8, 13, 21. Calcular Fibonacci(j) con 0≤j≤8 en este caso tendría un coste unitario que supondría acceder a la posición j-ésima del array. Previamente construir la sucesión de Fibonacci nos costaría un poco más, tanto como el máximo valor j. Pero si nuestra aplicación necesita con mucha frecuencia el valor de Fibonacci hasta un límite que supone un array que pueda ser almacenado sin afectar a los recursos de memoria, quizás es preferible generar y almacenar ese array para que esté disponible en cualquier momento de la ejecución.
Un enfoque podría ser no almacenar los valores de la sucesión al inicio, sino a medida que las necesitemos.
let tablaFibonacci = [0, 1];
function fibonacci(n){
numIter++;
if (n>tablaFibonacci.length) {
for (let i=tablaFibonacci.length; i<=n; i++){
numIter++;
tablaFibonacci.push(tablaFibonacci[i-1]+tablaFibonacci[i-2]);
}
}
return tablaFibonacci[n];
}Ejemplo: Fibonacci con Programación Dinámica
fibonacci(n): Devolver cambio: El principio de optimalidad
El principio de optimalidad afirma que en una secuencia óptima de decisiones, toda subsecuencia debe ser también óptima. Todo problema donde pueda aplicarse este principio es susceptible de resolverse con programación dinámica. La clave está en construir ascendentemente una tabla de resultados intermedios óptimos que nos servirá para obtener la solución final óptima.
En el tema sobre algoritmos voraces vimos el problema de devolver cambio. Demostramos que el conjunto de monedas del Euro con valores 1, 2, 5 era óptimo. Mientras que el conjunto 1, 3, 5, 6 no lo era, puesto que para devolver el valor 8 utilizaba tres monedas: una de 6 y dos de 1 unidad. Sin embargo se pueden devolver 8 con sólo dos monedas: una de 5 y una de 3.
En este problema puede aplicarse el principio de optimalidad. Construimos la tabla de resultados intermedios para devolver valores entre 0 y 8 con ese conjunto de monedas 1, 3, 5, 6. Cada posición representa el número mínimo de monedas a devolver. Por lo tanto cada posición, que se ha obtenido de forma óptima, se resuelve a su vez con las posiciones anteriores óptimas. Construyamos la tabla paso a paso, donde cada columna 0 ≤ v ≤ 8 representa un valor a devolver y cada fila m ∈ {1, 3, 5, 6} representa una moneda.
Empezamos con la moneda m = 1 y buscamos cuántas monedas mínimas son necesarias si sólo tuvieramos el conjunto de monedas M = {1}. La sólución es evidente, pues necesitamos tantas monedas de una unidad como el valor a devolver. Podemos afirmar que si v=1 entonces el número mínimo de monedas a devolver es el mismo que el valor v a devolver.
Ampliamos el conjunto con otra moneda M = {1, 3}. Rellenamos las columnas en la fila m = 3 comprobando primero si v < m, en cuyo caso el número de monedas mínimas es el mismo que el de la fila anterior. Es obvio que para devolver v = 1 < 3 necesitamos 1 moneda m = 1. Y que para devolver v = 2 < 3 necesitamos 2 monedas m = 1.
Si T[m, v] representa una posición de la tabla en la fila m y en la columna v, podemos afirmar que si 1 < m < v entonces la posición anterior T[m-1, v] nos dará el número mínimo de monedas.
En otro caso si v ≥ m tenemos dos posibilidades. Una es tomar el número de monedas de la fila anterior como antes, es decir, T[m-1, v]. La otra posibildad es tomar una moneda en esa posición [m, v] y buscar el número de monedas de una posición anterior en esa misma fila y en la columna dada por el valor restante v - m, quedando por tanto 1 + T[m, v-m] monedas mínimas. De las dos posibilidades optaremos por la que devuelva el menor número de monedas: Min(T[m-1, v], 1 + T[m, v-m]). Con este proceder generemos los valores que nos faltan en esa fila m = 3:
- Para v = 3 tenemos Min(T[1, 3], 1 + T[3, 0]) = Min(3, 1+0) = Min(3, 1) = 1
- Para v = 4 tenemos Min(T[1, 4], 1 + T[3, 1]) = Min(4, 1+1) = Min(4, 2) = 2
- Para v = 5 tenemos Min(T[1, 5], 1 + T[3, 2]) = Min(5, 1+2) = Min(5, 3) = 3
- Para v = 6 tenemos Min(T[1, 6], 1 + T[3, 3]) = Min(6, 1+1) = Min(6, 2) = 2
- Para v = 7 tenemos Min(T[1, 7], 1 + T[3, 4]) = Min(7, 1+2) = Min(7, 3) = 3
- Para v = 8 tenemos Min(T[1, 8], 1 + T[3, 5]) = Min(8, 1+3) = Min(8, 4) = 4
De la misma forma seguiremos avanzando hacia abajo por filas y en cada fila hacia la derecha por columnas, generando el número de monedas mínimas exclusivamente con los valores óptimos ya calculados en las posiciones anteriores, tal como se muestra en la tabla adjunta ya finalizada. Esta tabla de resultados intermedios nos dice el número mínimo de monedas, pero no nos dice cuáles son esas monedas. Luego veremos que esa información está implícita en la tabla, planteándose un algoritmo voraz para obtenerlo.
Vease que en cada momento resolvemos una posición posterior con otra anterior que ya fue resuelta de forma óptima. En el fondo la estrategia es ir resolviendo de forma óptima los casos más sencillos y apoyarnos en esos para resolver los siguientes. Es, por tanto, una secuencia de decisiones óptimas que deben llevarnos a un resultado final óptimo.
Devolver cambio con programación dinámica
Aplicando las ideas anteriores vamos ya a plantear el código para devolver cambio con programación dinámica. Haremos un ejemplo interactivo para resolver el problema también con el algoritmo voraz que vimos en un tema anterior, cuyo código era el siguiente:
function devolverCambioVoraz(valor=0, monedas=[]){
monedas = monedas.sort((a,b) => b-a));
numIter = 1 + monedas.length;
let cambio = monedas.map(() => 0);
let valorCambio = 0;
while (valorCambio < valor){
numIter++;
let j = 0;
for (j=0; j<monedas.length; j++){
numIter++;
if (valorCambio + monedas[j]<=valor) break;
}
if (j>=monedas.length) {
cambio = "Error: falta moneda unidad";
break;
}
cambio[j]++;
valorCambio += monedas[j];
}
return cambio;
}La programación dinámica es capaz de devolver siempre el mínimo número de monedas si tenemos al menos la moneda unidad con el siguiente código:
let coins = [], monedasBak = [], maxValue = 30;
function devolverCambio(valor=0, monedas=[]){
monedas = [0, ...monedas].sort((a,b) => a-b);
numIter++;
//TABLA DE RESULTADOS INTERMEDIOS: Monedas mínimas
if (monedas.join(",")!==monedasBak.join(",")) {
monedasBak = [...monedas];
coins = monedas.map(v => Array.from({length: maxValue+1}, () => 0));
for (let i=1; i<monedas.length; i++) {
numIter++;
for (let j=1; j<=maxValue; j++){
numIter++;
if (i===1) {
if (j<monedas[i]) {
coins[i][j] = Infinity;
} else {
coins[i][j] = 1 + coins[i][j-monedas[i]];
}
} else if (j<monedas[i]){
coins[i][j] = coins[i-1][j];
} else {
coins[i][j] = Math.min(coins[i-1][j], 1 + coins[i][j-monedas[i]]);
}
}
}
}
//BUCLE VORAZ
numIter += monedas.length;
let cambio = monedas.map(v => 0);
let j = valor;
for (let i=monedas.length-1; i>0 && j>0 && typeof cambio!=="string"; i--){
numIter++;
if (coins[i][j] !== coins[i-1][j]) {
if (j-monedas[i]<0) {
cambio = "Error: falta moneda unidad";
} else if (coins[i][j] === 1 + coins[i][j-monedas[i]]){
if (coins[i][j]===Infinity) {
cambio = "Error: falta moneda unidad";
} else {
while (j-monedas[i] >= 0){
cambio[i]++;
j -= monedas[i];
}
}
}
}
}
return cambio;
}Ejemplo: Devuelve cambio
devolverCambio(valor, monedas): devolverCambio(valor, monedas): Para el ejemplo que se carga inicialmente con la página, devolver un valor 8 con el array de monedas 0, 1, 3, 5, 6 genera 133 iteraciones la primera vez, cuando se construye el conjunto de monedas mínimas (array coins). En las siguientes ejecuciones si mantenemos el array de monedas observamos que el coste disminuye considerablemente. Ejecutar otra vez el valor 8 sólo lleva 9 iteraciones. Incluso algo inferior al algoritmo voraz sin programación dinámica que supone 17 iteraciones.
Por lo tanto la programación dinámica será más eficiente en un caso real si se necesitan múltiples ejecuciones del algoritmo manteniendo la misma tabla de datos. Pensemos en una máquina que tiene que devolver monedas. Sería posible que cuando la máquina arranque cargue la tabla de mondedas mínimas con valores hasta el máximo posible a devolver. Así en cada ejecución posterior ya tenemos ese coste asumido.
Construyendo la tabla de resultados intermedios
Veamos ahora como se construye realmente la tabla de resultados intermedios con la ejecución del código, que para nuestro problema la podemos denominar como tabla de monedas mínimas. Como ejemplo usaremos el array de monedas 0, 1, 3, 5, 6 y un valor a devolver de hasta 8 unidades. La parte del código que lo ejecuta es la siguiente:
//TABLA DE RESULTADOS INTERMEDIOS: Monedas mínimas
for (let i=1; i<monedas.length; i++) {
for (let j=1; j<=maxValue; j++){
if (i===1) {
if (j<monedas[i]) {
coins[i][j] = Infinity;
} else {
coins[i][j] = 1 + coins[i][j-monedas[i]];
}
} else if (j<monedas[i]){
coins[i][j] = coins[i-1][j];
} else {
coins[i][j]=Math.min(coins[i-1][j], 1+coins[i][j-monedas[i]]);
}
}
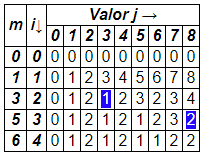
}| m | i↓ | Valor j → | ||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 2 | 0 | 1 | 2 | 1 | 2 | 3 | 2 | 3 | 4 |
| 5 | 3 | 0 | 1 | 2 | 1 | 2 | 1 | 2 | 3 | 2 |
| 6 | 4 | 0 | 1 | 2 | 1 | 2 | 1 | 1 | 2 | 2 |
La tabla de monedas mínimas (array coins) con valores hasta 8 que se obtiene es la que se observa en la Figura (filas i × columnas j). En la primera columna ponemos también el array de monedas (columna m). El array coins se inicializó previamente con una dimensión n×N = 5×9, siendo n=5 la longitud del array de monedas 0, 1, 3, 5, 6 y N=9 el valor máximo a devolver más uno.
Iteramos en el bucle i=1..4 que se corresponden con los índices de monedas 0, 1, 3, 5, 6. Por cada i iteramos en otro bucle j=1..8 que son los posibles valores a devolver. Observe que el array tiene los índices cero, pero las iteraciones las hacemos ignorando esa posición.
Cada posición coins[i][j] de la tabla de monedas mínimas nos dice el número de monedas mínimas necesarias para devolver el valor j usando sólo monedas menores o iguales al índice i. No nos dice qué monedas en el rango [1..i] hay que usar, sólo nos dice el número mínimo de monedas a devolver. Luego veremos que el bucle voraz nos dirá exactamente que monedas hay que devolver usando coins como conjunto de entrada del algoritmo voraz.
Veamos primero el caso i>1 en el código anterior. Si el valor a devolver j es menor que el valor de la moneda i-ésima monedas[i], entonces elegiremos la moneda anterior devolviendo coins[i-1][j] monedas. En otro caso si j≥monedas[i] tenemos dos posibilidades, debiendo elegir la que devuelva menos monedas. Una posibilidad es seleccionar la moneda anterior, como hicimos antes. La otra posibilidad es seleccionar 1 moneda de la clase i y buscar el número de monedas del valor restante j-monedas[i], es decir, devolvemos 1 + coins[i][j-monedas[i]]. Entre esas dos posibilidades elegiremos la menor que devolverá menos monedas.
Veamos ahora el caso cuando i=1. Si el valor a devolver es menor que la clase de moneda inicial, sucede que no podemos devolver ese valor y ponemos Infinity. Es el caso cuando no tenemos la moneda unidad por ejemplo. En otro caso devolvemos la segunda posibilidad de las que dijimos antes 1 + coins[1][j-monedas[1]].
Ejecutando el algoritmo voraz para devolver cambio
El algoritmo voraz siempre necesita un conjunto de datos para iterar por ellos y seleccionar los candidatos. Ese conjunto es precisamente la tabla de resultados intermedios que hemos obtenido con el array de monedas mínimas (coins). Vamos ahora a ejecutar el voraz, cuyo código volvemos a reproducir a continuación.
//BUCLE VORAZ
numIter += monedas.length;
let cambio = monedas.map(v => 0);
let j = valor;
for (let i=monedas.length-1; i>0 && j>0 && typeof cambio!=="string"; i--){
numIter++;
if (coins[i][j] !== coins[i-1][j]) {
if (j-monedas[i]<0) {
cambio = "Error: falta moneda unidad";
} else if (coins[i][j] === 1 + coins[i][j-monedas[i]]){
if (coins[i][j]===Infinity) {
cambio = "Error: falta moneda unidad";
} else {
while (j-monedas[i] >= 0){
cambio[i]++;
j -= monedas[i];
}
}
}
}
}| m | i↓ | Valor j → | ||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 2 | 0 | 1 | 2 | 1 | 2 | 3 | 2 | 3 | 4 |
| 5 | 3 | 0 | 1 | 2 | 1 | 2 | 1 | 2 | 3 | 2 |
| 6 | 4 | 0 | 1 | 2 | 1 | 2 | 1 | 1 | 2 | 2 |
En la Figura observará que para devolver un valor 8 hemos señalado dos posiciones en la tabla de monedas mínimas (coins). Esos lugares de la tabla se localizan con el algoritmo voraz que descubre las monedas a devolver rellenando el array cambio. Si el array de monedas es [0, 1, 3, 5, 6] y devolvemos un valor 8, lo hará devolviendo 1 moneda de 5 y 1 moneda de 3 unidades. Esto se estructura devolviendo el array de cambio [0, 0, 1, 1, 0] donde cada posición nos dice el número de monedas del array de monedas que hay que devolver. Veamos como funciona.
El valor j inicialmente es el valor a devolver 8 del problema. Iteramos descendentemente por las filas desde la i=4 hasta la i=1, observando coins[i][j] !== coins[i-1][j], cuando el valor de la columna es distinto de la fila anterior. Vemos que con i=4 la posición coins[4][8]=2, coins[3][8]=2, siendo iguales, por lo que en esta iteración no hacemos nada. En la siguiente tenemos coins[3][8]=2, coins[2][8]=4, siendo distintos, por lo que consideramos esta fila i=3. La posición coins[3][8]=2 significa que para devolver 8 necesitaremos un número mínimo de 2 monedas. Una de ellas es una moneda de valor de la fila i=3, es decir, monedas[3] = 5. El resto se obtiene restando j-monedas[i], es decir, 8-monedas[3] = 8-5 = 3.
El bucle while controlará aquellos casos cuando un valor puede devolverse con más de una moneda. Para el ejemplo de devolver 8 sólo se ejecuta una vez, puesto que la primera deja j=8-5=3 y la siguiente que no se ejecuta puesto que 3-5=-2 negativo. Pero si devolvemos el valor 10 con dos monedas de 5 vemos que el bucle se ejecuta dos veces: j=10-5=5 y j=5-5=0, resultando que acumulamos dos monedas de valor 5.
En cada iteración actualizaremos ese resto en la variable j. Hemos de llegar a un punto en que el resto sea cero, momento en que abandonaremos el bucle voraz. Si el resto j-monedas[i] es negativo indica que nos falta la moneda unidad. En otro caso observamos que el número de monedas de la posición actual coins[i][j] sea igual que el de la posición del resto más uno, es decir, de 1 + coins[i][j-monedas[i]]. En el ejemplo tenemos que 8-monedas[3]=8-5=3, coins[3][8]=2, 1+coins[3][3]=2 por lo que se cumple la condición. Esto viene a asegurar que el número de monedas del valor restante más una moneda del valor i-ésimo que estamos tratando es igual que el número de monedas de esta posición i-ésima.
En ese caso si el valor actual no es infinito, actualizamos el valor j quitando el valor de una moneda i-ésima. Y por otro lado agregamos una moneda en la posición i-ésima del array cambio. La única excepción sería que coins[i][j]=∞. En este caso se podría validar la condición coins[i][j] === 1 + coins[i][j-monedas[i]] si las posiciones en la tabla en ambas partes son ∞, puesto que 1+∞ = ∞. Detectamos esto poniendo una frase de que falta la moneda unidad en la variable cambio. Al salir del bucle for detectamos si cambio es un String, en cuyo caso salimos del bucle voraz exterior while.
El coste del algoritmo para devolver cambio
No perdemos genaralidad si consideramos que los arrays se inician en uno en lugar de cero. El problema se establece sobre n monedas para devolver un valor V. Supongamos que nos dan el array de monedas ya ordenado. Y también que no consideramos la opción de comprobar si el array de monedas ha cambiado en cada ejecución. Así para construir la tabla de resultados intermedios C (coins en el código) sólo tenemos un bucle doble i=1..n × j=1..V+1, con coste O(nV).
El bucle voraz crea el array cambio de longitud n. Y a continuación itera en i=n..0. En el interior el bucle while itera hacia atrás desde una posición coins[i][j] por la misma fila i. Pero lo hace en múltiplos de j, pues va restando j en cada iteración. Como mucho ese coste será el valor de la máxima posición de la tabla C[n][V], puesto que cada posición de la tabla nos dice el número de monedas que se devuelven. En definitiva, aunque son dos bucles for y while anidados, realmente el recorrido hasta alcanzar el valor cero es de un máximo de n por filas más un máximo de C[n][V] por columnas. El coste de esta parte es entonces la suma O(n + C[n][V]).