09 oct 2025

Árbol Gomory-Hu

Construir árbol Gomory-Hu `getGomoryHuTree()`

*Figura*. Grafo no dirigido y ponderado y su árbol Gomory-Hu

En un tema anterior expusimos que encontrar todos los cortes de aristas con el algoritmo findEdgeCut() suponía iterar por todas las parejas de nodos "s" y "t" encontrando las aristas que producen un corte mínimo usando el algoritmo findSTEdgeCut() y devolver todos los resultados ordenados por la suma de flujos creciente, siendo el primer resultado la solución con mínimo corte. Y un corte mínimo de aristas s-t que se ejecuta con findSTEdgeCut() supone encontrar un conjunto mínimo de aristas que separe los nodos "s" y "t" en distintos componentes conectados.

Iterar por todas las parejas de nodos "s,t" del grafo para encontrar el corte mímimo teóricamente puede resultar costoso si el número de nodos es muy grande. Existe una estructura denominada árbol de Gomory-Hu que, una vez construida con el algoritmo getGomoryHuTree(), permite fácilmente encontrar todos los cortes mínimos s-t. Sólo puede aplicarse a grafos no dirigidos y conectados. Y hemos de tenerlo en cuenta pues findSTEdgeCut() y por extensión findEdgeCut() puede aplicarse a grafos desconectados pues su objetivo es separar "s" y "t" en distintos componentes. Si inicialmente "s" y "t" están en distintos componentes entonces findSTEdgeCut() simplemente no devuelve nada pues ya están separados.

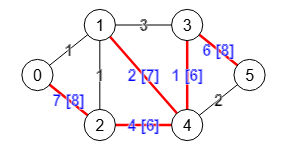
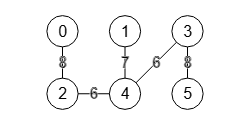
En la Figura vemos un grafo con su árbol Gomory-Hu resaltado, grafo que aparece en la página Gomory-Hu de Wikipedia y también en el PDF que puede verse en Flujos en grafos Gomory-Hu trees, sobre el que también vamos a explicar cómo construir un árbol Gomory-Hu. El resultado obtenido no es exactamente el mismo, puesto que un grafo puede tener varios de estos árboles, como explicaremos en el apartado sobre un grafo puede tener varios árboles Gomory-Hu.

Podemos resumir que el árbol Gomory-Hu de un grafo permite encontrar el corte mínimo de aristas con menor coste que otros algoritmos cuando se aplica sobre grafos no dirigidos y conectados y, especialmente, sobre grafos ponderados.

Se resaltan las aristas que forman parte del árbol Gomory-Hu, con el peso obtenido entre corchetes. Hay que aclarar que Gomory-Hu es un árbol de cubrimiento de todos los nodos del grafo. Aunque no es el caso, sus aristas pueden no existir en el grafo, como veremos en un apartado más abajo cuando hablemos sobre las nuevas aristas en árbol Gomory-Hu.

En la aplicación con el algoritmo getGomoryHuTree() obtenemos el siguiente resultado:

Obtener árbol Gomory-Hu: {
"matrix":
[[0,0,8,0,0,0],
[0,0,0,0,7,0],
[8,0,0,0,6,0],
[0,0,0,0,6,8],
[0,7,6,6,0,0],
[0,0,0,8,0,0]],
"vertexTree":[0,2,4,1,3,5],
"edgeTree":[[2,4],[0,2],[3,4],[1,4],[3,5]],
"weightTree":[6,8,6,7,8],
"verification":[],
"warnings":[],
"trace":""}

El campo "matrix" del resultado anterior contiene la matriz de adyacencia del árbol Gomory-Hu, matriz que se construye al final a partir de los campos "vertexTree" como lista de vértices del árbol, "edgeTree" como lista de aristas y "weightTree" como lista de pesos. En "trace" se puede obtener una traza si marcamos la opción trazar árbol que puede observar en la Figura. La opción verificar chequea el resultado devolviéndolo en el campo "verification", como explicaremos en el apartado verificar el resultado al obtener el árbol Gomory-Hu. El campo "warnings" devuelve avisos sin que se corte la ejecución. La opción forzar no dirigido es para aplicar sobre grafos dirigidos y obtener el árbol de su conversión a no dirigido, pues Gomory-Hu es sólo para no dirigidos.

Hay que tener claro que pueden existir varios árboles Gomory-Hu para un mismo grafo, como el ejemplo que usamos en este apartado y que hemos tomado de la página de Wikipedia que hemos mencionado. El resultado obtenido aquí es diferente al de esa página, pero podemos forzarlo para que sean iguales con la opción muestra como explicamos en el apartado sobre un grafo puede tener varios árboles Gomory-Hu.

La aplicación vierte el árbol en pantalla, pero también puede importar la matriz de adyacencia "matrix". Si importa la lista de aristas "edgeTree" recuerde que no puede presentar los pesos que están en "weightTree".

La opción método para flujo puede ser "findPath", "dijkstra" o "floyd". En todos los ejemplos usamos "findPath", pues este algoritmo getGomoryHuTree() usa findSTEdgeCut() que a su vez necesita un algoritmo para encontrar un camino entre dos nodos usando por defecto el algoritmo findPath(), aunque pueden ser más eficientes los algoritmos "dijkstra" con getShortestPathDijkstra() o "floyd" con getShortestPathFloyd() que encuentran un camino mínimo entre dos nodos más eficientemente. Más abajo veremos un ejemplo sobre esto.

Con el siguiente JSON puede importar el ejemplo, en este caso con la opción trazar ábol (traceTree) marcada:

{"nodes":[
    {"index":0,"nodeOffset":"-1.67 17.5","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"-10 -27.5","parent":[{"index":0,"value":1}]},
    {"index":2,"nodeOffset":"6.67 37.5","parent":[{"index":-1},{"index":0,"value":7},{"index":1,"value":1}]},
    {"index":3,"nodeOffset":"25 -2.5","parent":[{"index":-1},{"index":1,"value":3}]},
    {"index":4,"nodeOffset":"8.33 37.5","parent":[{"index":-1},{"index":2,"value":4},{"index":1,"value":2},{"index":3,"value":1}]},
    {"index":5,"nodeOffset":"16.67 17.5","parent":[{"index":-1},{"index":3,"value":6},{"index":4,"value":2}]}
],
"config":{
    "algorithm":"Get Gomory-Hu tree",
    "traceTree":true
}}

Si el grafo tiene n nodos, el algoritmo Gomory-Hu garantiza que el árbol puede construirse en n-1 pasos. Cuando consideremos el coste veremos que la reducción del coste en relación con findEdgeCut() va a depender de las operaciones internas en cada paso, pues hay que hacer varias cosas como se observa en el siguiente esquema del algoritmo getGomoryHuTree():

Entrada: grafo no dirigido, conectado y ponderado G con V = [0, 1, 2, ..., n-1] vértices
Salida: árbol T con vertexTree vértices, edgeTree aristas y weightTree pesos

vertexTree = [V]
edgeTree = []
weightTree = []
Mientras ∃ subset ∈ vertexTree tal que subset.length > 1
    Seleccionar par vértices s,t de subset
    Obtener resto vértices en T
    Hacer un copia de G en G'
    Contraer resto de vértices en G'
    Obtener corte s-t findStEdgeCut() en G'
    Borrar aristas del corte en G'
    Obtener componentes conectados en G'
    Actualizar T con vertexTree, edgeTree y weightTree
Obtener matriz a partir de vertexTree, edgeTree y weightTree
Devolver resultado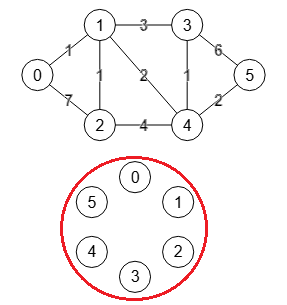

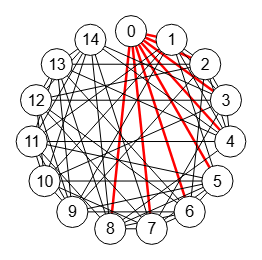
El grafo de ejemplo que vamos a usar para seguir la construción del árbol Gomory-Hu tiene 6 nodos, con los que necesitaremos 5 pasos para completarlo. En la Figura vemos la situación al inicio. En la parte superior se presenta una copia del grafo G', pues hay que copiarlo dado que en cada paso ejecutaremos operaciones sobre el mismo que lo modifican. En la parte inferior se presenta el árbol T Gomory-Hu.

Al inicio G'=G y en T tenemos un único nodo con todos los vértices de G, quedando vertexTree = [[0,1,2,3,4,5]], edgeTree = [] y weightTree = [], tres variables que identifican el árbol T.

Step 1
vertexTree:[[0,1,2,3,4,5]]
Get subset:[0,1,2,3,4,5]
Remove subset from vertexTree
Set s=0, t=1 from subset
Get remainingVertexs:[]
Contract remainingVertexs:[]
matrixCopy:[[0,1,7,0,0,0],[1,0,1,3,2,0],[7,1,0,0,4,0],[0,3,0,0,1,6],[0,2,4,1,0,2],[0,0,0,6,2,0]]
Contract matrixCopy:[[0,1,7,0,0,0],[1,0,1,3,2,0],[7,1,0,0,4,0],[0,3,0,0,1,6],[0,2,4,1,0,2],[0,0,0,6,2,0]]
labels:[]
Find s=0(0) t=1(1) edge cut:[[0,1],[2,1],[2,4]]
weight:6
Delete cut edges [[0,1],[2,1],[2,4]]
Get connected components: [[0,2],[1,3,4,5]]
componentsLabels:[[0,2],[1,3,4,5]] ([A',B'])
Update T
    X = [0,1,2,3,4,5] (subset)
    S = [] (remainingVertexs)
    A' = [0,2]
    B' = [1,3,4,5]
    A'∩X = [0,2]
    B'∩X = [1,3,4,5]
    As = ⋃ Sc ∈ A'∩S = []
    Bs = ⋃ Sc ∈ B'∩S = []
    A = As ⋃ A'∩X = [0,2]
    B = Bs ⋃ B'∩X = [1,3,4,5]
    A∩X = [0,2]
    B∩X = [1,3,4,5]
vertexTree.push(A∩X, B∩X)
edgeTree.push([A∩X,B∩X])
vertexTree:[[0,2],[1,3,4,5]]
edgeTree:[[[0,2],[1,3,4,5]]]
weightTree:[6]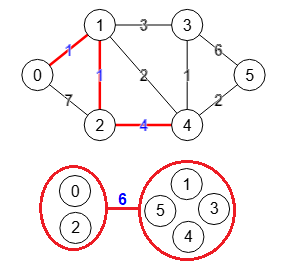

El texto que está antes de la Figura es la traza obtenida en la aplicación reflejando el estado de las variables que intervienen en el paso 1. Vemos que vertexTree:[[0,1,2,3,4,5]] había quedando antes con un único nodo [0,1,2,3,4,5] con todos los vértices de G. Elegimos como subconjunto subset a ese único nodo de T y seleccionamos s=0, t=1 los dos primeros nodos. Vea que cuando hablamos de nodos de T contamos con que pueden agrupar 1 o más nodos de G, rodeándose con un cerramiento circular en color rojo en el grafo inferior. Como el resto de vértices reminingSubsets es vacío no contraemos G', con lo que G'= G en este primer paso.

Encontramos el corte mínimo s=0 t=1 en G' con findSTEdgeCut() obteniendo las aristas [[0,1],[2,1],[2,4]] que tiene una suma de pesos 1+1+4=6. El corte en G' produce los componentes [[0,2],[1,3,4,5]] que separan s-t y que ahora son los dos nodos de T que actualizamos en vertexTree. La primera arista entre esos dos nodos de T tiene un peso 6 que actualizamos en weightTree. Esto quiere decir que separar [0,2] de [1,3,4,5] tiene un peso mínimo 6.

El siguiente paso es actualizar T que se indica en la traza con Update T. En este primer paso no hay vértices restantes remainingVertexs, por lo que al final la actualización agrega los vértices [0,2] y [1,3,4,5] a vertexTree, la arista [[0,2],[1,3,4,5]] a EdgeTree y el peso 6 a weightTree. En el paso siguiente explicaremos mejor este bloque.

Step 2
vertexTree:[[0,2],[1,3,4,5]]
Get subset:[0,2]
Remove subset from vertexTree
Set s=0, t=2 from subset
Get remainingVertexs:[[1,3,4,5]]
Contract remainingVertexs:[[1,3,4,5]]
matrixCopy:[[0,1,7,0,0,0],[1,0,1,3,2,0],[7,1,0,0,4,0],[0,3,0,0,1,6],[0,2,4,1,0,2],[0,0,0,6,2,0]]
Contract matrixCopy:[[0,1,7],[1,0,5],[7,5,0]]
labels:[[0],[1,3,4,5],[2]]
Find s=0(0) t=2(2) edge cut:[[0,1],[0,2]]
weight:8
Delete cut edges [[0,1],[0,2]]
Get connected components: [[0],[1,2]]
componentsLabels:[[0],[[1,3,4,5],2]] ([A',B'])
Udpate T
    X = [0,2] (subset)
    S = [[1,3,4,5]] (remainingVertexs)
    A' = [0]
    B' = [[1,3,4,5],2]
    A'∩X = [0]
    B'∩X = [2]
    As = ⋃ Sc ∈ A'∩S = []
    Bs = ⋃ Sc ∈ B'∩S = [[1,3,4,5]]
    A = As ⋃ A'∩X = [0]
    B = Bs ⋃ B'∩X = [1,3,4,5,2]
    A∩X = [0]
    B∩X = [2]
vertexTree.push(A∩X, B∩X)
edgeTree.push([A∩X,B∩X])
[[0,2],[1,3,4,5]] ∈ edgeTree and [1,3,4,5] ⊂ B  ⇒ replace it with [B∩X, [1,3,4,5]]
vertexTree:[[1,3,4,5],[0],[2]]
edgeTree:[[[2],[1,3,4,5]],[[0],[2]]]
weightTree:[6,8]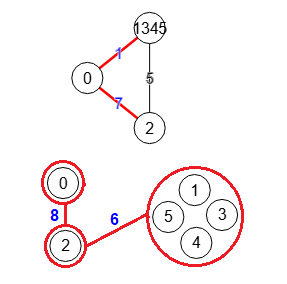

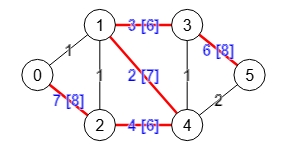
En la Figura vemos el paso 2 con la traza en el texto previo. Habíamos dejado los vértices del árbol vertexTree con dos nodos [[0,2],[1,3,4,5]]. Seleccionamos el primer subconjunto subset con más de 1 elemento resultando [0,2], de donde tomamos s=0, t=2. Se elimina subset de vertexTree.

En el grafo T del paso anterior teníamos los dos vértices [0,2] y [1,3,4,5] de tal forma que si quitamos [0,2] nos queda un único componente conectado [1,3,4,5] que en la traza denominamos remainingVertexs que son los componentes conectados en T tras eliminar subset, componentes que se filtran con los que tengan más de un elemento para finalmente contraerlos en G', puesto que contraer un componente con un único elemento no modifica el grafo.

Para contraer remainingVertexs:[[1,3,4,5]] hacemos una copia de G de la matriz original en G' con matrixCopy y luego contraemos en esa copia los vértices 1,3,4,5, quedando un grafo con menor número de vértices, pues si inicialmente tenía 6 al contraer 4 queda un grafo con 3 vértices, uno de ellos será el que agrupa 1,3,4,5. Para poder identificarlos con el grafo G usamos la variable etiquetas labels:[[0],[1,3,4,5],[2]] que hace corresponder los vértices de G' [0,1,2] con los de G [0,1,2,3,4,5], correspondencia que necesitaremos para el siguiente paso. El grafo G' contraído puede observarse en el grafo superior de la Figura (ver operación contraer nodos).

Luego aplicamos el corte de aristas para s=0, t=2 en G', obteniéndose 2 aristas de corte [[0,1],[0,2]] con un peso 8 como se observa en la parte superior de la Figura. A continuación borramos esas aristas en G' y obtenemos los componentes conectados [[0],[1,2]] también en G', que se corresponde con las etiquetas componentsLabels:[[0],[[1,3,4,5],2]] en G.

En el algoritmo getGomoryHuTree() hemos seguido el esquema expuesto en la página Gomory-Hu de Wikipedia tal como habíamos comentado, si bien tratamos los nombres de las variables para que sean significativos, por ejemplo, V_T ≡ vertexTree, E_T ≡ edgeTree, X ≡ subset, S_C ≡ remainingVertexs por ejemplo. Así también (A', B') ≡ componentsLabels, con lo que A' = [0] y B' = [[1,3,4,5],2]

A continuación actualizamos T en Update T de la traza, pasos que siguen el esquema y sus nombres de variables del algoritmo de Wikipedia. Obtenemos A, B, A∩X, B∩X que nos permitirán actualizar vertexTree:[[1,3,4,5],[0],[2]] y edgeTree:[[[2],[1,3,4,5]],[[0],[2]]], que con weightTree:[6,8] representa el grafo T que puede observarse en el grafo inferior de la Figura.

Step 3
vertexTree:[[1,3,4,5],[0],[2]]
Get subset:[1,3,4,5]
Remove subset from vertexTree
Set s=1, t=3 from subset
Get remainingVertexs:[[0,2]]
Contract remainingVertexs:[[0,2]]
matrixCopy:[[0,1,7,0,0,0],[1,0,1,3,2,0],[7,1,0,0,4,0],[0,3,0,0,1,6],[0,2,4,1,0,2],[0,0,0,6,2,0]]
Contract matrixCopy:[[0,2,0,4,0],[2,0,3,2,0],[0,3,0,1,6],[4,2,1,0,2],[0,0,6,2,0]]
labels:[[0,2],[1],[3],[4],[5]]
Find s=1(1) t=3(2) edge cut:[[1,2],[3,2],[3,4]]
weight:6
Delete cut edges [[1,2],[3,2],[3,4]]
Get connected components: [[0,1,3],[2,4]]
componentsLabels:[[[0,2],1,4],[3,5]] ([A',B'])
Update T
    X = [1,3,4,5] (subset)
    S = [[0,2]] (remainingVertexs)
    A' = [[0,2],1,4]
    B' = [3,5]
    A'∩X = [1,4]
    B'∩X = [3,5]
    As = ⋃ Sc ∈ A'∩S = [[0,2]]
    Bs = ⋃ Sc ∈ B'∩S = []
    A = As ⋃ A'∩X = [0,2,1,4]
    B = Bs ⋃ B'∩X = [3,5]
    A∩X = [1,4]
    B∩X = [3,5]
vertexTree.push(A∩X, B∩X)
edgeTree.push([A∩X,B∩X])
[[1,3,4,5],[2]] ∈ edgeTree and [2] ⊂ A  ⇒ replace it with [A∩X, [2]]
vertexTree:[[0],[2],[1,4],[3,5]]
edgeTree:[[[1,4],[2]],[[0],[2]],[[1,4],[3,5]]]
weightTree:[6,8,6]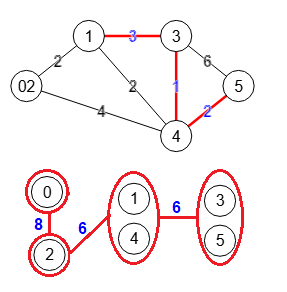

Vemos en la Figura el paso 3 con la traza en el texto previo. Teníamos vertexTree del paso anterior con [[1,3,4,5],[0],[2]]. Seleccionamos el subconjunto subset=[1,3,4,5] con más de un elemento. De ahí seleccionamos los dos primeros s=1 y t=3.

Los subconjuntos restantes de vertexTree resultan ser [[0],[2]] con los que formamos los vértices restantes remainingVertexs = [[0,2]]. Vea que T había quedado con 3 nodos conectados con aristas {[1,3,4,5]} - {[2]} - {[0]} de tal forma que si eliminamos el nodo [1,3,4,5] queda un único componente conectado {[2]} - {[0]}. Por eso remainingVertexs = [[0],[2]] que se obtiene eliminando [1,3,4,5] en la lista de aristas anterior edgeTree:[[[2],[1,3,4,5]],[[0],[2]]]. Así que remainingVertexs = [[0,2]] es el único componente conectado que contraemos en una copia G' del grafo original G quedando como vemos en el grafo superior de la Figura con las etiquetas labels:[[0,2],[1],[3],[4],[5]] de correspondencia entre G' y G.

Ejecutamos findSTEdgeCut() para encontrar el corte s=1, t=3 en G, que tras aplicar la correspondencia de etiquetas equivale al corte s=1, t=2 en G'. Se obtienen las aristas [[1,2],[3,2],[3,4]] de G', que tras eliminarlas obtenemos los componentes conectados [[0,1,3],[2,4]] en G' que se corresponden con las etiquetas componentsLabels:[[[0,2],1,4],[3,5]] en G. El peso del corte es 3+1+2=6 obtenido de los pesos de la matriz de G'.

Actualizamos el árbol T quedando vertexTree:[[0],[2],[1,4],[3,5]], edgeTree:[[[1,4],[2]],[[0],[2]],[[1,4],[3,5]]] y weightTree:[6,8,6], observando en el grafo T de la parte inferior de la Figura que hemos conseguido separar el nodo [1,3,4,5] en dos nodos [1,4] y [3,5].

Step 4
vertexTree:[[0],[2],[1,4],[3,5]]
Get subset:[1,4]
Remove subset from vertexTree
Set s=1, t=4 from subset
Get remainingVertexs:[[0,2],[3,5]]
Contract remainingVertexs:[[0,2],[3,5]]
matrixCopy:[[0,1,7,0,0,0],[1,0,1,3,2,0],[7,1,0,0,4,0],[0,3,0,0,1,6],[0,2,4,1,0,2],[0,0,0,6,2,0]]
Contract matrixCopy:[[0,2,0,4],[2,0,3,2],[0,3,0,3],[4,2,3,0]]
labels:[[0,2],[1],[3,5],[4]]
Find s=1(1) t=4(3) edge cut:[[1,0],[1,2],[1,3]]
weight:7
Delete cut edges [[1,0],[1,2],[1,3]]
Get connected components: [[0,3,2],[1]]
componentsLabels:[[[0,2],4,[3,5]],[1]] ([A',B'])
Update T
    X = [1,4] (subset)
    S = [[0,2],[3,5]] (remainingVertexs)
    A' = [[0,2],4,[3,5]]
    B' = [1]
    A'∩X = [4]
    B'∩X = [1]
    As = ⋃ Sc ∈ A'∩S = [[0,2],[3,5]]
    Bs = ⋃ Sc ∈ B'∩S = []
    A = As ⋃ A'∩X = [0,2,3,5,4]
    B = Bs ⋃ B'∩X = [1]
    A∩X = [4]
    B∩X = [1]
vertexTree.push(A∩X, B∩X)
edgeTree.push([A∩X,B∩X])
[[1,4],[2]] ∈ edgeTree and [2] ⊂ A  ⇒ replace it with [A∩X, [2]]
[[1,4],[3,5]] ∈ edgeTree and [3,5] ⊂ A  ⇒ replace it with [A∩X, [3,5]]
vertexTree:[[0],[2],[3,5],[4],[1]]
edgeTree:[[[4],[2]],[[0],[2]],[[4],[3,5]],[[4],[1]]]
weightTree:[6,8,6,7]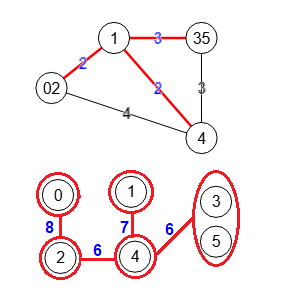

En la Figura vemos el paso 4 con la traza de las variables en el texto previo. La lista de vértices había quedado en el paso anterior con vertexTree = [[0],[2],[1,4],[3,5]]. El primer subconjunto con más de un elemento es subset = [1,4] donde seleccionamos s=1, t=4.

En el paso anterior teníamos en T los vértices con aristas {[0]}-{[2]}-{[1,4]}-{[3,5]} de tal forma que si eliminamos el vértice [1,4] nos quedan dos componentes conectados {[0]}-{[2]} y {[3,5]}. Por eso remaningVertexs = [[0,2],[3,5]] que son los dos componentes conectados que procedemos a contraer, primero [0,2] y después [3,5] quedando el grafo G' como se observa en la parte superior de la Figura. La correspondencia de etiquetas es labels = [[0,2],[1],[3,5],[4]] por lo que el corte s=1, t=4 en G se corresponde con s=1, t=3 en G'.

Ese corte con peso 2+2+3=7 tras borrar las aristas de corte obtenemos los componentes conectados [[0,3,2],[1]] en G' que se corresponden con componentsLabels: [[[0,2],4,[3,5]],[1]] en G.

Actualizamos T observando en el grafo inferior de la Figura que hemos separado 1 y 4 con respecto al T anterior.

Step 5
vertexTree:[[0],[2],[3,5],[4],[1]]
Get subset:[3,5]
Remove subset from vertexTree
Set s=3, t=5 from subset
Get remainingVertexs:[[0,2,4,1]]
Contract remainingVertexs:[[0,2,4,1]]
matrixCopy:[[0,1,7,0,0,0],[1,0,1,3,2,0],[7,1,0,0,4,0],[0,3,0,0,1,6],[0,2,4,1,0,2],[0,0,0,6,2,0]]
Contract matrixCopy:[[0,4,2],[4,0,6],[2,6,0]]
labels:[[0,1,2,4],[3],[5]]
Find s=3(1) t=5(2) edge cut:[[0,2],[1,2]]
weight:8
Delete cut edges [[0,2],[1,2]]
Get connected components: [[0,1],[2]]
componentsLabels:[[[0,1,2,4],3],[5]] ([A',B'])
Update T
    X = [3,5] (subset)
    S = [[0,2,4,1]] (remainingVertexs)
    A' = [[0,1,2,4],3]
    B' = [5]
    A'∩X = [3]
    B'∩X = [5]
    As = ⋃ Sc ∈ A'∩S = [[0,1,2,4]]
    Bs = ⋃ Sc ∈ B'∩S = []
    A = As ⋃ A'∩X = [0,1,2,4,3]
    B = Bs ⋃ B'∩X = [5]
    A∩X = [3]
    B∩X = [5]
vertexTree.push(A∩X, B∩X)
edgeTree.push([A∩X,B∩X])
[[3,5],[4]] ∈ edgeTree and [4] ⊂ A  ⇒ replace it with [A∩X, [4]]
vertexTree:[[0],[2],[4],[1],[3],[5]]
edgeTree:[[[4],[2]],[[0],[2]],[[3],[4]],[[4],[1]],[[3],[5]]]
weightTree:[6,8,6,7,8]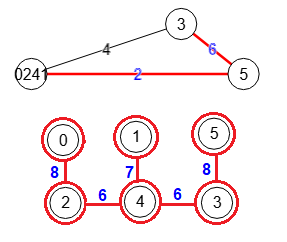

En la Figura vemos el paso 5 y último con la traza de variables en el texto previo. La lista de vértices había quedado vertexTree = [[0],[2],[3,5],[4],[1]] en el paso anterior, observando que en este último paso vamos a separar el nodo [3,5] de T, último que queda con más de un elemento y que selecionamos en subset = [3,5], con s=3, t=5.

En el paso anterior teníamos en T los vértices con aristas {[0]}-{[2]}-{[4]}-{[3,5]} y también {[4]}-{[1]}. Si eliminamos el vértice [3,5] nos queda un único componente conectado {[0]}-{[2]}-{[4]}-{[1]}. Así remaningVertexs = [[0,2,4,1]] es el único componente conectado que contraemos obteniendo el grafo G' de la parte superior de la Figura. La correspondencia de etiquetas labels: [[0,1,2,4],[3],[5]] nos dice que hemos de hacer el corte en G' con s=1, t=2, que tras eliminar las aristas de corte obtenemos los componentes conectados [[0,1],[2]] en G' que se corresponde con componentsLabels:[[[0,1,2,4],3],[5]] en G. El corte tiene un peso 2+6=8.

Con esto ya separamos [3] y [5] quedando la lista de vértices vertexTree: [[0],[2],[4],[1],[3],[5]] con todos los nodos con un único vértice y, por tanto, habremos finalizado. La lista de aristas queda edgeTree: [[[4],[2]],[[0],[2]],[[3],[4]],[[4],[1]],[[3],[5]]] y la lista de pesos weightTree = [6,8,6,7,8].

[[0,0,8,0,0,0],
[0,0,0,0,7,0],
[8,0,0,0,6,0],
[0,0,0,0,6,8],
[0,7,6,6,0,0],
[0,0,0,8,0,0]]

Devolvemos la lista de vértices como vertexTree = [0,2,4,1,3,5] y la lista de aristas como edgeTree = [[2,4],[0,2],[3,4],[1,4],[3,5]] omitiendo el nivel más profundo de corchetes. La lista de pesos no se modifica weightTree = [6,8,6,7,8]. Usando la lista de aristas y la de pesos construimos la matriz de adyacencia adjunta que también se devuelve.

Importando esa matriz en la aplicación obtenemos el grafo de la Figura que es el mismo del inferior del último paso en la Figura. Vemos la disposición final en forma de árbol de esta estructura Gomory-Hu, cuya finalidad explicaremos en un siguente apartado.

En la aplicación resaltamos el árbol Gomory-Hu sobre el grafo original, con los pesos entre corchetes en cada arista, como se observa en la Figura. Recordamos que el árbol es un recubrimiento de todos los nodos, aunque no necesariamente cubre aristas existentes, pues pueden aparecer nuevas aristas como veremos en un ejemplo en el apartado nuevas aristas en árbol Gomory-Hu.

Un grafo puede tener varios árboles Gomory-Hu

Un grafo puede tener varios árboles Gomory-Hu. En la Figura vemos otro árbol Gomory-Hu sobre el mismo grafo que utilizamos en el apartado anterior, ejemplo que vemos en Gomory-Hu de Wikipedia y también en Flujos en grafos Gomory-Hu trees, coincidendo el árbol obtenido en este caso. En las opciones que expusimos en la Figura vimos la opción muestra que estando marcada fuerza la obtención del resultado de la Figura en lugar del obtenido en el apartado anterior en la Figura, con este resultado:

Obtener árbol Gomory-Hu: {
"matrix":
[[0,0,8,0,0,0],
[0,0,0,6,7,0],
[8,0,0,0,6,0],
[0,6,0,0,0,8],
[0,7,6,0,0,0],
[0,0,0,8,0,0]],
"vertexTree":[3,5,4,1,0,2],
"edgeTree":[[1,3],[3,5],[2,4],[1,4],[0,2]],
"weightTree":[6,8,6,7,8],
"verification":[],
"warnings":[],
"trace":""}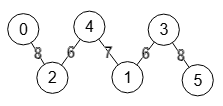

En la página de Wikipedia puede observar el árbol de la Figura, que hemos obtenido en la aplicación tras importar la matriz de adyacencia del resultado anterior.

Puede importar el ejemplo con este JSON.

{"nodes":[
    {"index":0,"nodeOffset":"-1.67 17.5","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"-10 -27.5","parent":[{"index":0,"value":1}]},
    {"index":2,"nodeOffset":"6.67 37.5","parent":[{"index":-1},{"index":0,"value":7},{"index":1,"value":1}]},
    {"index":3,"nodeOffset":"25 -2.5","parent":[{"index":-1},{"index":1,"value":3}]},
    {"index":4,"nodeOffset":"8.33 37.5","parent":[{"index":-1},{"index":2,"value":4},{"index":1,"value":2},{"index":3,"value":1}]},
    {"index":5,"nodeOffset":"16.67 17.5","parent":[{"index":-1},{"index":3,"value":6},{"index":4,"value":2}]}
],
"config":{
    "algorithm":"Get Gomory-Hu tree",
    "traceTree":true,
    "sample":true
}}

Vamos a explicar en la tabla siguiente el grupo Version 1 con variables que expusimos en el primer apartado y la Version 2 (Wikipedia) con el ejemplo de esa página web.

Step	Version 1				Version 2 (Wikipedia)
Step	vertexTree	subset	s,t	findSTEdgeCut()	vertexTree	subset	s,t	findSTEdgeCut()
1	[[0,1,2,3,4,5]]	[0,1,2,3,4,5]	0,1	[[0,1],[2,1],[2,4]]	[[0,1,2,3,4,5]]	[0,1,2,3,4,5]	1,5	[[1,3],[4,3],[4,5]]
2	[[0,2],[1,3,4,5]]	[0,2]	0,2	[[0,1],[0,2]]	[[0,1,2,4],[3,5]]	[3,5]	3,5	[[0,2],[1,2]]
3	[[1,3,4,5],[0],[2]]	[1,3,4,5]	1,3	[[1,2],[3,2],[3,4]]	[[0,1,2,4],[3],[5]]	[0,1,2,4]	1,2	[[1,0],[1,2],[4,2]]
4	[[0],[2],[1,4],[3,5]]	[1,4]	1,4	[[1,0],[1,2],[1,3]]	[[3],[5],[0,2],[1,4]]	[1,4]	1,4	[[1,0],[2,3],[1,3]]
5	[[0],[2],[3,5],[4],[1]]	[3,5]	3,5	[[0,2],[1,2]]	[[3],[5],[0,2],[4],[1]]	[0,2]	0,2	[[0,1],[0,2]]

En primer lugar no hay ninguna limitación para seleccionar algún subset con tamaño mayor de uno en vertexTree o bien los vértices "s" y "t" en subset. Vemos por ejemplo que en el primer paso nosotros seleccionadmos "s,t=0,1" mientras que Wikipedia selecciona "s,t=1,5". Nuestro criterio es tomar los dos primeros "s" y "t" de subset, no sabiendo el criterio que se aplica en Wikipedia igualmente válido.

Siempre seleccionamos el primer subset con tamaño mayor de uno en vertexTree, como por ejemplo en el segundo paso, que seleccionamos subset = [0,2] mientras que en Wikipedia se selecciona el segundo [3,5] sin motivarlo pero igualmente válido. Distintos s,t producen distintos cortes findSTEdgeCut().

En el paso cuarto vemos que ambos "s,t" son iguales 1,4 y ambos vértices restantes remainingVertexs también son iguales. Sin embargo los cortes son distintos:

Step 4 (Version 1)
...
Get remainingVertexs:[[0,2],[3,5]]
Contract remainingVertexs:[[0,2],[3,5]]
matrixCopy:[[0,1,7,0,0,0],[1,0,1,3,2,0],[7,1,0,0,4,0],[0,3,0,0,1,6],[0,2,4,1,0,2],[0,0,0,6,2,0]]
Contract matrixCopy:[[0,2,0,4],[2,0,3,2],[0,3,0,3],[4,2,3,0]]
labels:[[0,2],[1],[3,5],[4]]
Find s=1(1) t=4(3) edge cut:[[1,0],[1,2],[1,3]]
...

Step 4 (Version 2 Wikipedia)
...
Get remainingVertexs:[[3,5],[0,2]]
Contract remainingVertexs:[[3,5],[0,2]]
matrixCopy:[[0,1,7,0,0,0],[1,0,1,3,2,0],[7,1,0,0,4,0],[0,3,0,0,1,6],[0,2,4,1,0,2],[0,0,0,6,2,0]]
Contract matrixCopy:[[0,2,0,4],[2,0,3,2],[0,3,0,3],[4,2,3,0]]
labels:[[0,2],[1],[3,5],[4]]
Find s=1(1) t=4(3) edge cut:[[1,0],[2,3],[1,3]]
...

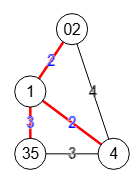
En ambos casos obtenemos los mismos vértices restantes Get remainingVertexs:[[0,2],[3,5]] y por tanto la misma matriz contraída Contract matrixCopy:[[0,2,0,4],[2,0,3,2],[0,3,0,3],[4,2,3,0]]. Si en la aplicación importamos la copia de la matriz matrixCopy, contraemos los nodos etiquetados 1 y 4 con índices 1 y 3, aplicamos el corte findSTEdgeCut() obtenemos la lista de aristas [[1,0],[1,2],[1,3]] que se corresponde con los vértices etiquetados [[1,[3,5]], [1,[0,2]], [1,4]], como se observa en la Figura.

El algoritmo findSTEdgeCut() devuelve el primer corte con peso mínimo, pues si observamos la Figura encontraremos los cortes que separan los nodos etiquetados "1,4" con índices "1,3" siguientes, recordando que las etiquetas son labels:[[0,2],[1],[3,5],[4]] iguales en ambos casos:

[[1,[3,5]], [1,[0,2]], [1,4]] con peso 3+2+2 = 7 que es la que aparece en la Figura con índices etiquetados [[1,0],[1,2],[1,3]]
[[1,[0,2]], [[3,5],4], [1,4]]] con peso 2+3+2 = 7 con índices [[1,0],[2,3],[1,3]]
[[1,[3,5]], [1,4], [[0,2],4]] con peso 3+2+4 = 9 que no es peso mínimo
[[[3,5],4], [1,4], [[0,2],4] con peso 3+2+4 = 9 que no es peso mínimo

Por lo tanto hay dos cortes con peso mínimo 7 y, dependiendo del algoritmo para encontrarlos, cualquiera de ellos puede ser posible. En el algorimo de Wikipedia opta por el segundo [[1,0],[2,3],[1,3]], forzándolo así en la aplicación cuando activamos la opción muestra, tras lo cual se llega a un árbol Gomory-Hu distinto al de la versión 1, pero igual que el de Wikipedia e igualmente válido.

Finalidad del árbol Gomory-Hu: encontrar mínimo corte de aristas con Gomory-Hu `findEdgeCutGomoryHu()`

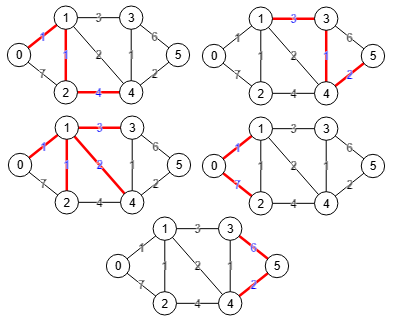
En el primer apartado obtuvimos el árbol Gomory-Hu del grafo que vemos en la Figura. Ahora vamos a ver qué hacemos con ese árbol una vez obtenido, recordando que el resultado que devovía getGomoryHuTree() era el siguiente:

Obtener árbol Gomory-Hu: {
"matrix":
[[0,0,8,0,0,0],
[0,0,0,0,7,0],
[8,0,0,0,6,0],
[0,0,0,0,6,8],
[0,7,6,6,0,0],
[0,0,0,8,0,0]],
"vertexTree":[0,2,4,1,3,5],
"edgeTree":[[2,4],[0,2],[3,4],[1,4],[3,5]],
"weightTree":[6,8,6,7,8],
"verification":[],
"warnings":[],
"trace":""}

El árbol se resalta sobre el grafo inicial en la aplicación y también puede importarse por medio de la matriz de adyacencia del resultado, tal como vemos en la Figura. Las aristas entre nodos "s,t" en ese árbol representan el peso del corte que separa "s" y "t" en dos componentes conectados. Vemos que "2,4" y "3,4" tienen peso 6, siendo entonces las parejas de nodos en el grafo inicial cuya separación tiene menor peso. Obviamente esto nos sirve para encontrar el corte mínimo de aristas en un grafo.

{"nodes":[
    {"index":0,"nodeOffset":"-1.67 17.5","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"-10 -27.5","parent":[{"index":0,"value":1}]},
    {"index":2,"nodeOffset":"6.67 37.5","parent":[{"index":-1},{"index":0,"value":7},{"index":1,"value":1}]},
    {"index":3,"nodeOffset":"25 -2.5","parent":[{"index":-1},{"index":1,"value":3}]},
    {"index":4,"nodeOffset":"8.33 37.5","parent":[{"index":-1},{"index":2,"value":4},{"index":1,"value":2},{"index":3,"value":1}]},
    {"index":5,"nodeOffset":"16.67 17.5","parent":[{"index":-1},{"index":3,"value":6},{"index":4,"value":2}]}
],
"config":{
    "algorithm":"Get Gomory-Hu tree",
    "traceTree":true
}}

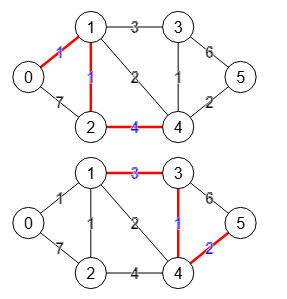
Usando el mismo grafo obtenemos los cortes de aristas usando el algoritmo findEdgeCut() que vimos en un tema anterior, obteniendo los cinco cortes que vemos en la Figura. Esos cortes están ordenados por peso creciente, de tal forma que los primeros son los de menor peso, los dos primeros en este caso pues la suma de los pesos de las aristas de corte resultan 6.

Esos grafos de la Figura son la representación del resultado del algoritmo findEdgeCut(), donde el campo "edges" devuelve los cinco cortes y el campo "st" devuelve las parejas de nodos "s" y "t" que producen cada uno de los cortes.

Encontrar corte aristas: {
"edges":[
    [[0,1],[1,2],[2,4]],
    [[1,3],[3,4],[4,5]],
    [[0,1],[1,2],[1,3],[1,4]],
    [[0,1],[0,2]],
    [[3,5],[4,5]]
],
"st":[
    [[0,1],[0,3],[0,4],[0,5],[1,2],[2,3],[2,4],[2,5]],
    [[1,3],[1,5],[3,4],[4,5]],
    [[1,4]],
    [[0,2]],
    [[3,5]]
],
"stEmpty":[],
"warnings":[]}

Recordando que en el Gomory-Hu obtuvimos "edgeTree": [[2,4],[0,2],[3,4],[1,4],[3,5]] y "weightTree": [6,8,6,7,8], confrontándolo con el resultado del corte findEdgeCut() anterior vemos la siguiente tabla:

findEdgeCut()
"s,t" for findEdgeCut()	Edges of cut	Weight
[[0,1],[0,3],[0,4],[0,5],[1,2],[2,3],[2,4],[2,5]]	[[0,1],[1,2],[2,4]]	1+1+4=6
[[1,3],[1,5],[3,4],[4,5]]	[[1,3],[3,4],[4,5]]	3+1+2=6
[[1,4]]	[[0,1],[1,2],[1,3],[1,4]]	1+1+2+3=7
[[0,2]]	[[0,1],[0,2]]	1+7=8
[[3,5]]	[[3,5],[4,5]]	6+2=8

Ya hemos dicho que para construir el árbol Gomory-Hu sobre un grafo con n nodos sólo necesitamos probar n-1 cortes de aristas, tal como vimos en la tabla de un apartado anterior donde exponíamos que los cortes "s,t" a ejecutar con findSTEdgeCut() que se producían eran s,t = [[0,1], [0,2], [1,3], [1,4], [3,5]], en total 5 cortes que vemos resaltados en la tabla anterior, uno menos que el total de nodos 6 del grafo. Sin embargo para ejecutar findEdgeCut() necesitamos ejecutar findSTEdgeCut() en 15 cortes, tal como vemos en la tabla anterior contando todas las parejas "s,t" de la primera columna, pues son las combinaciones de 6 nodos tomados en parejas de 2, que obedece a la fórmula del binomial C(6, 2) = 15, así que nos ahorramos 10 ejecuciones de findSTEdgeCut().

Si estamos buscando el mínimo de todos los cortes vemos que con findEdgeCut() devolverá el primero, pues ese algoritmo los busca todos, los ordena por el peso y será el primero el mínimo. Aunque en este caso los dos primeros pueden considerar mínimos al tener el mismo peso. Obteniendo el árbol Gomory-Hu de la Figura sólo tenemos que buscar la arista o aristas con menor peso, que resultan ser s,t=[2,4] con corte [[0,1],[1,2],[2,4]] y s,t=[3,4] con corte [[1,3],[3,4],[4,5]], los dos primeros de la lista de cortes ordenada por peso creciente que devuelve findEdgeCut() que vemos en la tabla anterior.

En la aplicación agregamos el nuevo algoritmo getEdgeCutGomoryHu() para encontrar el corte mínimo de aristas usando el árbol Gomory-Hu. Recordamos otra vez que habíamos obtenido las aristas del árbol "edgeTree": [[2,4],[0,2],[3,4],[1,4],[3,5]] con los pesos "weightTree": [6,8,6,7,8], siendo los cortes mínimos los resaltados en azul, tal como se observa en el árbol de la Figura.

Este algoritmo findEdgeCutGomoryHu() nos devuelve los dos primeros cortes con peso 6, que son los mínimos de todos los cortes que vimos en la Figura usando el algoritmo findEdgeCut().

Encontrar corte aristas Gomory-Hu: [
    {"edges":[[0,1],[2,1],[2,4]],"s":2,"t":4,"weight":6},
    {"edges":[[3,1],[3,4],[5,4]],"s":3,"t":4,"weight":6}
]

{"nodes":[
    {"index":0,"nodeOffset":"-1.67 17.5","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"-10 -27.5","parent":[{"index":0,"value":1}]},
    {"index":2,"nodeOffset":"6.67 37.5","parent":[{"index":-1},{"index":0,"value":7},{"index":1,"value":1}]},
    {"index":3,"nodeOffset":"25 -2.5","parent":[{"index":-1},{"index":1,"value":3}]},
    {"index":4,"nodeOffset":"8.33 37.5","parent":[{"index":-1},{"index":2,"value":4},{"index":1,"value":2},{"index":3,"value":1}]},
    {"index":5,"nodeOffset":"16.67 17.5","parent":[{"index":-1},{"index":3,"value":6},{"index":4,"value":2}]}
],
"config":{
    "algorithm":"Find edge cut Gomory-Hu"
}}

El JavaScript para ejecutar findEdgeCutGomoryHu() se expone a continuación.

function findEdgeCutGomoryHu({matrix=[], methodFlow="findPath", forceUndirected="false"}) {
    let result = [], temp;
    try {
        let directed = isGraphDirected({matrix});
        if (typeof directed==="string") throw new Error(directed);
        if (directed) {
            if (!forceUndirected) {
                throw new Error(`The graph is directed and should be applied to undirected graphs or use the force undirected option`);
            } else {
                if (temp = operateDirectionGraph({matrix, edgesDirection:"undirected"}), temp.error) throw new Error(temp.error);
                matrix = temp.matrix;
            }
        }
        if (temp = getGomoryHuTree({matrix, methodFlow, forceUndirected}), typeof temp==="string") throw new Error(temp);
        let edgeTree = temp.edgeTree;
        let weightTree = temp.weightTree;
        let edgeWeightTree = edgeTree.map((v,i) => [...v, weightTree[i]]);
        edgeWeightTree.sort((v,w) => v[2]-w[2]);
        let min = edgeWeightTree[0][2];
        edgeWeightTree = edgeWeightTree.filter(v => v[2]===min);
        for (let item of edgeWeightTree) {
            let [s, t, weight] = item;
            if (temp = findSTEdgeCut({matrix, firstIndex:s, lastIndex:t, methodFlow}), typeof temp==="string") throw new Error(temp);
            let edges = temp;
            result.push({edges, s, t, weight});
        }
    } catch(e) {result = e.message}
    return result;
}

Usa los algoritmos y operaciones siguientes:

isGraphDirected() para saber si un grafo es dirigido pues el algoritmo para obtener el árbol Gomory-Hu sólo puede aplicarse a grafos no dirigidos.
operateDirectionGraph() para convertir a no dirigido el grafo dirigido en caso de que la opción forzar no dirigido (argumento forceUndirected) se pase marcado.
getGomoryHuTree() para construir el árbol Gomory Hu cuyo algoritmo veremos a continuación.
findSTEdgeCut() para encontrar las aristas del corte mínimo obtenidas del resultado Gomory Hu.

Algoritmo para obtener el árbol Gomory-Hu `getGomoryHuTree()`

A continuación exponemos el JavaScript del algoritmo getGomoryHuTree().

function getGomoryHuTree({matrix=[], methodFlow="findPath", forceUndirected="false", directed=null, verify=false}){
    let result = {matrix: [], vertexTree: [], edgeTree: [], weightTree: [], verification:[], warnings:[]}, temp;
    try {
        if (directed===null) {
            directed = isGraphDirected({matrix});
            if (typeof directed==="string") throw new Error(directed);
        }
        if (directed) {
            if (!forceUndirected) {
                throw new Error(`The graph is directed and should be applied to undirected graphs or use the force undirected option`);
            } else {
                if (temp = operateDirectionGraph({matrix, edgesDirection:"undirected"}), temp.error) throw new Error(temp.error);
                matrix = temp.matrix;
            }
        }
        if (temp = isGraphConnected({matrix}), typeof temp==="string") throw new Error(temp);
        let connected = temp;
        if (!connected) throw new Error(`The graph is not connected and Gomory-Hu cannot be applied`);
        let n = matrix.length;
        let vertexTree = [Array.from({length:n}, (v,i)=>i)]; // ET
        let edgeTree = []; // VT
        let weightTree = []; // c
        let itemTrace = 0;
        let kset = -1;
        while (kset = vertexTree.findIndex(v => v.length>1), kset>-1) {
            iter++;
            if (iter>maxIter) {
                result.warnings.push(`Maximum iterations '${maxIter}' reached`);
                break;
            }
            // Seleccionar par vértices s,t de subset
            let vertexTreeT = JSON.parse(JSON.stringify(vertexTree));
            let subset = vertexTree.splice(kset, 1)[0]; // X
            let [s, t] = subset;
            // Obtener resto vértices en T
            let remainingVertexs = []; // SC
            if (edgeTree.length>0) {
                let edgesT = edgeTree.map(v => v.map(w => vertexTreeT.findIndex(x => x.toString()===w.toString())));
                if (temp = convertToAdjacencyMatrix({array:edgesT, mode:"edgeList", compactUndirected:true}), temp.error) throw new Error(temp.error);
                let matrixT = temp.matrix;
                if (temp = operateEditionGraph({matrix:matrixT, edges:[[kset, -1]], edition:"delete"}), temp.error) throw new Error(temp.error);
                matrixT = temp.matrix;
                if (temp = getConnectedComponents({matrix:matrixT}), typeof temp==="string") throw new Error(temp);
                remainingVertexs = temp.map(v => v.visited).map(v => v.map(w => vertexTree[w])).map(v => v.flat());
            }
            // Hacer un copia de G en G'
            let matrixCopy = JSON.parse(JSON.stringify(matrix));
            // Contraer resto de vértices en G'
            let labels = [];
            for (let indexes of remainingVertexs) {
                if (indexes.length>1) {
                    let indexs = [];
                    if (labels.length>0) {
                        for (let index of indexes) {
                            let j = labels.findIndex(v => v.includes(index));
                            if (j===-1) throw new Error(j);
                            indexs.push(j);
                        }
                    } else {
                        indexs = [...indexes];
                    }
                    if (temp = operateContractionGraph({matrix:matrixCopy, indexes:indexs, typeMergedValue:"sum", omitSelfLoops:true}), temp.error) {
                        result.warnings.push("(operateContractionGraph) " + temp.error);
                        break;
                    }
                    matrixCopy = temp.matrix;
                    if (labels.length>0) {
                        let labelsCopy = JSON.parse(JSON.stringify(labels));
                        labels = [];
                        for (let item of temp.labels) {
                            let arr = [];
                            for (let v of item) {
                                arr.push(...labelsCopy[v]);
                            }
                            labels.push(arr);
                        }
                    } else {
                        labels = temp.labels;
                    }
                }
            }
            // Obtener corte s-t findStEdgeCut() en G'
            let [firstIndex, lastIndex] = [s, t];
            if (labels.length>0) {
                firstIndex = labels.findIndex(v => v.length===1 && v[0]===s);
                if (firstIndex===-1) throw new Error(`Error in first index`);
                lastIndex = labels.findIndex(v => v.length===1 && v[0]===t);
                if (lastIndex===-1) throw new Error(`Error in last index`);
            }
            let tempIter = iter;
            iter = 0;
            if (temp = findSTEdgeCut({matrix:matrixCopy, firstIndex, lastIndex, methodFlow}), typeof temp==="string") {
                result.warnings.push("(findSTEdgeCut) " + temp);
                break;
            }
            iter = tempIter;
            let edges = temp;
            if (edges.length===0) result.warnings.push(`There is no edges in s=${s} t=${t} cut`);
            let weight = 0;
            for (let edge of edges) {
                let [i, j] = edge;
                weight += matrixCopy[i][j];
            }
            weightTree.push(weight); // w((A∩X, B∩X))
            // Borrar aristas del corte en G'
            if (temp = operateEditionGraph({matrix:matrixCopy, edges, edition:"delete"}), temp.error) {
                result.warnings.push("(operateEditionGraph) " + temp.error);
                break;
            }
            matrixCopy = temp.matrix;
            tempIter = iter;
            iter = 0;
            // Obtener componentes conectados en G'
            if (temp = getConnectedComponents({matrix:matrixCopy}), typeof temp==="string") {
                result.warnings.push("getConnectedComponents() " + temp);
                return result;
            }
            iter = tempIter;
            let components = temp.map(v => v.visited);
            let componentsLabels = [];
            if (labels.length>0) {
                for (let component of components) {
                    let arr = [];
                    for (let v of component) {
                        arr.push(labels[v]);
                    }
                    componentsLabels.push(arr);
                }
            } else {
                componentsLabels = components;
            }
            componentsLabels = componentsLabels.map(v => v.map(w => w.length===1 ? w[0] : w));
            // Actualizar T con vertexTree, edgeTree y weightTree
            let [a, b] = componentsLabels; // A', B'
            if (typeof a==="undefined") {
                result.warnings.push(`Component A' is undefined`);
                return result;
            }
            if (typeof b==="undefined") {
                result.warnings.push(`Component B' is undefined`);
                return result;
            }
            a = a.map(v => Array.isArray(v) ? v.toSorted((v,w) => v-w) : v);
            b = b.map(v => Array.isArray(v) ? v.toSorted((v,w) => v-w) : v);
            let aix = a.filter(v => subset.includes(v)); // A'∩X
            let bix = b.filter(v => subset.includes(v)); // B'∩X
            let as = a.filter(v => remainingVertexs.some(w => w.toSorted((v,w) => v-w).toString()===v.toString())); //As = ⋃ Sc ∈ A'∩S
            let bs = b.filter(v => remainingVertexs.some(w => w.toSorted((v,w) => v-w).toString()===v.toString())); //Bs = ⋃ Sc ∈ B'∩S
            let acs = [...as, ...aix].flat(); // A = As ⋃ A'∩X
            let bcs = [...bs, ...bix].flat(); // B = Bs ⋃ B'∩X
            let ac = acs.filter(v => subset.includes(v)); // A∩X
            let bc = bcs.filter(v => subset.includes(v)); // B∩X
            vertexTree.push(ac, bc); // VT = (VT\X) ⋃ {A∩X, B∩X}
            if (edgeTree.length>0) {
                let st = subset.toString();
                for (let i=0; i<edgeTree.length; i++) {
                    let [x, y] = edgeTree[i];
                    let z = x.toString()===st ? y : y.toString()===st ? x : null;
                    if (z!==null) {
                        let zz = JSON.stringify(z);
                        if (z.every(v => acs.includes(v))) { // Y⊂A
                            edgeTree[i] = [ac, z]; // e' = (A∩X, Y), ET = (ET\{e}) ⋃ {e'}
                        } else if (z.every(v => bcs.includes(v))) { // Y⊂B
                            edgeTree[i] = [bc, z]; // e' = (B∩X, Y), ET = (ET\{e}) ⋃ {e'}
                        }
                    }
                }
            }
            edgeTree.push([ac, bc]); // ET = ET ⋃ {(A∩X,B∩X)}
        }
        // Obtener matriz a partir de vertexTree, edgeTree y weightTree
        // Devolver resultado
        if (result.warnings.length>0) {
            result.vertexTree = vertexTree;
            result.edgeTree = edgeTree;
        } else {
            result.vertexTree = vertexTree.map(v => v[0]);
            if (result.vertexTree.length<matrix.length) result.warnings.push(`The vertex tree does not have all the nodes`);
            if (result.edgeTree.some(v => v[0].length>1 || b[1].length>1)) result.warnings.push(`There are edges wrong`);
            result.edgeTree = edgeTree.map(v => [v[0][0], v[1][0]].toSorted((v,w)=>v-w));
            result.weightTree = weightTree;
            if (temp = convertToAdjacencyMatrix({array:result.edgeTree, mode:"edgeList", compactUndirected:true}), temp.error) throw new Error(temp.error);
            result.matrix = temp.matrix;
            for (let k=0; k<result.weightTree.length; k++) {
                let [i, j] = result.edgeTree[k];
                let weight = result.weightTree[k];
                result.matrix[i][j] = weight;
                result.matrix[j][i] = weight;
            }
            if (verify) {
                let arr = [];
                let ok = true;
                for (let i = 0; i<result.edgeTree.length; i++){
                    let edge = result.edgeTree[i];
                    let [firstIndex, lastIndex] = edge;
                    if (temp = findSTEdgeCut({matrix, firstIndex, lastIndex, methodFlow}), typeof temp==="string") throw new Error(temp);
                    let edges = temp;
                    let weight = edges.reduce((p,v) => (p+=matrix[v[0]][v[1]], p), 0);
                    if (weight!==result.weightTree[i]) ok = false;
                    let car = weight===result.weightTree[i] ? "==" : "!=";
                    arr.push(`Weight cut ${edge[0]}-${edge[1]} ==  weightTree[${i}] ⇒ ${weight} ${car} ${result.weightTree[i]} ⇒ ${ok}`);
                }
                result.verification = [ok, arr];
            }
        }
    } catch(e) {result = e.message}
    return result;
}

Por claridad hemos omitido el código relacionado con las opciones trazar árbol y muestra que ya explicamos en apartados anteriores. El esquema del algoritmo ya lo expusimos al principio y volvemos a reproducir aquí, poniendo líneas de comentarios en el código anterior con cada paso del bucle while principal:

Entrada: grafo no dirigido, conectado y ponderado G con V = [0, 1, 2, ..., n-1] vértices
Salida: árbol T con vertexTree vértices, edgeTree aristas y weightTree pesos

vertexTree = [V]
edgeTree = []
weightTree = []
Mientras ∃ subset ∈ vertexTree tal que subset.length > 1
    Seleccionar par vértices s,t de subset
    Obtener resto vértices en T
    Hacer un copia de G en G'
    Contraer resto de vértices en G'
    Obtener corte s-t findStEdgeCut() en G'
    Borrar aristas del corte en G'
    Obtener componentes conectados en G'
    Actualizar T con vertexTree, edgeTree y weightTree
Obtener matriz a partir de vertexTree, edgeTree y weightTree
Devolver resultado

He tratado de seguir el esquema matemático expuesto en la página de Gomory-Hu de Wikipedia que ya hemos mencionado y que no incluye implementaciones. Dice esa página que el algoritmo de Gusfield puede usarse para encontrar el árbol Gomory-Hu sin utilizar contracción de vértices, pero en esta versión lo he implementado directamente desde el esquema expuesto. Se inicia con una partición en T que incluye todos los nodos de G y en cada paso vamos separando esa partición hasta que tengamos tantas como nodos tiene G, o lo que es lo mismo, finalizando con particiones con un único nodo.

En el algoritmo tratamos los nombres de las variables para que sean significativos, incluyendo comentarios al final de algunas sentencias para observar la equivalencia con el expuesto en Wikipedia. La equivalencia de las variables principales son:

V_T ≡ vertexTree
E_T ≡ edgeTree
w(k), k ∈ E_T ≡ weightTree[k]
X ≡ subset
s,t ≡ s,t
S_C ≡ remainingVertexs

Se usan los siguientes algoritmos y operaciones:

isGraphDirected() para saber si un grafo es dirigido pues el algoritmo para obtener el árbol Gomory-Hu sólo puede aplicarse a grafos no dirigidos.
operateDirectionGraph() para convertir a no dirigido el grafo dirigido en caso de que la opción forzar no dirigido (argumento forceUndirected) se pase marcado.
isGraphConnected() para saber si el grafo es conectado pues el algoritmo para obtener el árbol Gomory-Hu sólo puede aplicarse a grafos conectados.
convertToAdjacencyMatrix() para convertir una lista de arista en una matriz de adyacencia, necesaria en la parte del algoritmo para obtener resto vértices en T y al final al obtener la matriz que se devuelve.
operateContractionGraph() para contrer un grafo en la parte del algoritmo contraer resto de vértices en G'.
findSTEdgeCut() para encontrar las aristas de corte s,t en la parte del algoritmo para obtener corte s-t findStEdgeCut() en G'.
operateEditionGraph() para borrar vértices o aristas en la matriz de adyacencia que se usa en la parte del algoritmo para obtener resto vértices en T y tras aplicar el corte s-t eliminar las aristas de corte.
getConnectedComponents() para obtener los componentes conectados en la parte del algoritmo para obtener resto vértices en T y tras aplicar el corte s-t y eliminar las aristas de corte.

Consideraciones sobre el coste del algoritmo Gomory-Hu con un ejemplo

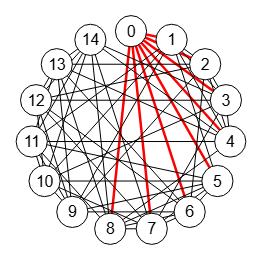
El grafo Johnson 6,2 tiene 15 nodos y 60 aristas. En la Figura vemos el primer corte de aristas de los 14 posibles aplicando el algoritmo findEdgeCut(). Como vimos en la Figura, la opción máximas iteraciones se establece para todos los algoritmos con un valor inicial de 10000 iteraciones.

En caso de superarse, el algoritmo finaliza devolviendo los resultados alcanzados hasta ese momento y un aviso en color rojo (FindSTEdgeCut) Maximum iterations 10000 reached testing s=0 t=5.

El algoritmo findEdgeCut() ejecuta findSTEdgeCut() para todas las parejas de nodos "s,t" del grafo, como hay C(15, 2) = 105 parejas posibles, el algoritmo necesitará más de 10000 iteraciones para cubrirlas todas. Así con un máximo de 10000 vemos por el mensaje que sólo pudo llegar hasta la pareja "s=0 t=5" devolviendo sólo el primer resultado.

En cambio asignando 487000 máximas iteraciones el algoritmo completa el resultado siguiente sin avisos de error con un tiempo mínimo de ejecución de 117 ms.

Time: 117 ms

Encontrar corte aristas: {
"edges":
[[[0,1],[0,2],[0,3],[0,4],[0,5],[0,6],[0,7],[0,8]],
[[0,1],[1,2],[1,3],[1,4],[1,5],[1,9],[1,10],[1,11]],
[[0,2],[1,2],[2,3],[2,4],[2,6],[2,9],[2,12],[2,13]],
[[0,3],[1,3],[2,3],[3,4],[3,7],[3,10],[3,12],[3,14]],
[[0,4],[1,4],[2,4],[3,4],[4,8],[4,11],[4,13],[4,14]],
[[0,5],[1,5],[5,6],[5,7],[5,8],[5,9],[5,10],[5,11]],
[[0,6],[2,6],[5,6],[6,7],[6,8],[6,9],[6,12],[6,13]],
[[0,7],[3,7],[5,7],[6,7],[7,8],[7,10],[7,12],[7,14]],
[[0,8],[4,8],[5,8],[6,8],[7,8],[8,11],[8,13],[8,14]],
[[1,9],[2,9],[5,9],[6,9],[9,10],[9,11],[9,12],[9,13]],
[[1,10],[3,10],[5,10],[7,10],[9,10],[10,11],[10,12],[10,14]],
[[1,11],[4,11],[5,11],[8,11],[9,11],[10,11],[11,13],[11,14]],
[[2,12],[3,12],[6,12],[7,12],[9,12],[10,12],[12,13],[12,14]],
[[2,13],[4,13],[6,13],[8,13],[9,13],[11,13],[12,13],[13,14]]],
"st":
[[[0,1],[0,2],[0,3],[0,4],[0,5],[0,6],[0,7],[0,8],[0,9],[0,10],[0,11],[0,12],[0,13],[0,14]],
[[1,2],[1,3],[1,4],[1,5],[1,6],[1,7],[1,8],[1,9],[1,10],[1,11],[1,12],[1,13],[1,14]],
[[2,3],[2,4],[2,5],[2,6],[2,7],[2,8],[2,9],[2,10],[2,11],[2,12],[2,13],[2,14]],
[[3,4],[3,5],[3,6],[3,7],[3,8],[3,9],[3,10],[3,11],[3,12],[3,13],[3,14]],
[[4,5],[4,6],[4,7],[4,8],[4,9],[4,10],[4,11],[4,12],[4,13],[4,14]],
[[5,6],[5,7],[5,8],[5,9],[5,10],[5,11],[5,12],[5,13],[5,14]],
[[6,7],[6,8],[6,9],[6,10],[6,11],[6,12],[6,13],[6,14]],
[[7,8],[7,9],[7,10],[7,11],[7,12],[7,13],[7,14]],
[[8,9],[8,10],[8,11],[8,12],[8,13],[8,14]],
[[9,10],[9,11],[9,12],[9,13],[9,14]],
[[10,11],[10,12],[10,13],[10,14]],
[[11,12],[11,13],[11,14]],
[[12,13],[12,14]],
[[13,14]]],
"stEmpty":[],
"warnings":[]}

{"nodes":[
    {"index":0,"nodeOffset":"2.5","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"57.66 -21.54","parent":[{"index":0}]},
    {"index":2,"nodeOffset":"60.01 -11.77","parent":[{"index":0},{"index":1}]},
    {"index":3,"nodeOffset":"57.21 2.64","parent":[{"index":0},{"index":1},{"index":2}]},
    {"index":4,"nodeOffset":"47.84 19.18","parent":[{"index":0},{"index":1},{"index":2},{"index":3}]},
    {"index":5,"nodeOffset":"31.58 35","parent":[{"index":0},{"index":1}]},
    {"index":6,"nodeOffset":"9.34 47.36","parent":[{"index":0},{"index":2},{"index":5}]},
    {"index":7,"nodeOffset":"-16.96 54.13","parent":[{"index":0},{"index":3},{"index":5},{"index":6}]},
    {"index":8,"nodeOffset":"-44.71 54.13","parent":[{"index":0},{"index":4},{"index":5},{"index":6},{"index":7}]},
    {"index":9,"nodeOffset":"14.7 22.36","parent":[{"index":1},{"index":2},{"index":5},{"index":6}]},
    {"index":10,"nodeOffset":"-10.71 10","parent":[{"index":1},{"index":3},{"index":5},{"index":7},{"index":9}]},
    {"index":11,"nodeOffset":"-30.14 -5.82","parent":[{"index":1},{"index":4},{"index":5},{"index":8},{"index":9},{"index":10}]},
    {"index":12,"nodeOffset":"-42.68 -22.36","parent":[{"index":2},{"index":3},{"index":6},{"index":7},{"index":9},{"index":10}]},
    {"index":13,"nodeOffset":"-48.66 -36.77","parent":[{"index":2},{"index":4},{"index":6},{"index":8},{"index":9},{"index":11},{"index":12}]},
    {"index":14,"nodeOffset":"-49.48 -46.54","parent":[{"index":3},{"index":4},{"index":7},{"index":8},{"index":10},{"index":11},{"index":12},{"index":13}]}
],
"config":{
    "algorithm":"Find edge cut",
    "maxIter":487000
}}

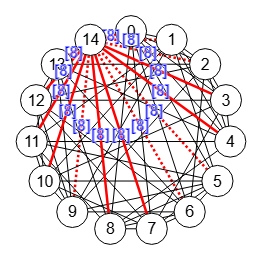
Ejecutando getGomoryHuTree() sólo necesitamos 12000 máximas iteraciones con un tiempo de ejecución mínimo de 9 ms.

Time: 9 ms

Obtener árbol Gomory-Hu: {
"matrix":
[[0,0,0,0,0,0,0,0,0,0,0,0,0,0,8],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,8],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,8],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,8],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,8],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,8],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,8],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,8],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,8],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,8],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,8],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,8],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,8],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,8],
[8,8,8,8,8,8,8,8,8,8,8,8,8,8,0]],
"vertexTree":[0,1,2,3,4,7,8,11,5,6,10,12,9,14,13],
"edgeTree":[[0,14],[1,14],[2,14],[3,14],[4,14],[7,14],[8,14],[11,14],[5,14],[6,14],[10,14],[12,14],[9,14],[13,14]],
"weightTree":[8,8,8,8,8,8,8,8,8,8,8,8,8,8],
"verification":[],
"warnings":[],
"trace":""}

{"nodes":[
    {"index":0,"nodeOffset":"2.5","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"57.66 -21.54","parent":[{"index":0}]},
    {"index":2,"nodeOffset":"60.01 -11.77","parent":[{"index":0},{"index":1}]},
    {"index":3,"nodeOffset":"57.21 2.64","parent":[{"index":0},{"index":1},{"index":2}]},
    {"index":4,"nodeOffset":"47.84 19.18","parent":[{"index":0},{"index":1},{"index":2},{"index":3}]},
    {"index":5,"nodeOffset":"31.58 35","parent":[{"index":0},{"index":1}]},
    {"index":6,"nodeOffset":"9.34 47.36","parent":[{"index":0},{"index":2},{"index":5}]},
    {"index":7,"nodeOffset":"-16.96 54.13","parent":[{"index":0},{"index":3},{"index":5},{"index":6}]},
    {"index":8,"nodeOffset":"-44.71 54.13","parent":[{"index":0},{"index":4},{"index":5},{"index":6},{"index":7}]},
    {"index":9,"nodeOffset":"14.7 22.36","parent":[{"index":1},{"index":2},{"index":5},{"index":6}]},
    {"index":10,"nodeOffset":"-10.71 10","parent":[{"index":1},{"index":3},{"index":5},{"index":7},{"index":9}]},
    {"index":11,"nodeOffset":"-30.14 -5.82","parent":[{"index":1},{"index":4},{"index":5},{"index":8},{"index":9},{"index":10}]},
    {"index":12,"nodeOffset":"-42.68 -22.36","parent":[{"index":2},{"index":3},{"index":6},{"index":7},{"index":9},{"index":10}]},
    {"index":13,"nodeOffset":"-48.66 -36.77","parent":[{"index":2},{"index":4},{"index":6},{"index":8},{"index":9},{"index":11},{"index":12}]},
    {"index":14,"nodeOffset":"-49.48 -46.54","parent":[{"index":3},{"index":4},{"index":7},{"index":8},{"index":10},{"index":11},{"index":12},{"index":13}]}
],
"config":{
    "algorithm":"Get Gomory-Hu tree",
    "maxIter":12000
}}

Pero debemos comparar findEdgeCut() de la Figura que necesitaba 487000 máximas iteraciones y un tiempo mínimo de ejecución de 117 ms con findEdgeCutGomoryHu() que vemos en la Figura, que sólo necesita 15000 máximas iteraciones y un tiempo de ejecución mínimo de 14 ms. La mejora en tiempo de ejecución es de (14-117) / 117 = -0.88, es decir, una mejora de un 88 %.

Time: 14 ms

Encontrar corte aristas Gomory-Hu: [
{"edges":[[0,1],[0,2],[0,3],[0,4],[0,5],[0,6],[0,7],[0,8]],"s":0,"t":14,"weight":8},
{"edges":[[1,0],[1,2],[1,3],[1,4],[1,5],[1,9],[1,10],[1,11]],"s":1,"t":14,"weight":8},
{"edges":[[2,0],[2,1],[2,3],[2,4],[2,6],[2,9],[2,12],[2,13]],"s":2,"t":14,"weight":8},
{"edges":[[3,0],[3,1],[3,2],[3,4],[3,7],[3,10],[3,12],[3,14]],"s":3,"t":14,"weight":8},
{"edges":[[4,0],[4,1],[4,2],[4,3],[4,8],[4,11],[4,13],[4,14]],"s":4,"t":14,"weight":8},
{"edges":[[7,0],[7,3],[7,5],[7,6],[7,8],[7,10],[7,12],[7,14]],"s":7,"t":14,"weight":8},
{"edges":[[8,0],[8,4],[8,5],[8,6],[8,7],[8,11],[8,13],[8,14]],"s":8,"t":14,"weight":8},
{"edges":[[11,1],[11,4],[11,5],[11,8],[11,9],[11,10],[11,13],[11,14]],"s":11,"t":14,"weight":8},
{"edges":[[5,0],[5,1],[5,6],[5,7],[5,8],[5,9],[5,10],[5,11]],"s":5,"t":14,"weight":8},
{"edges":[[6,0],[6,2],[6,5],[6,7],[6,8],[6,9],[6,12],[6,13]],"s":6,"t":14,"weight":8},
{"edges":[[10,1],[10,3],[10,5],[10,7],[10,9],[10,11],[10,12],[10,14]],"s":10,"t":14,"weight":8},
{"edges":[[12,2],[12,3],[12,6],[12,7],[12,9],[12,10],[12,13],[12,14]],"s":12,"t":14,"weight":8},
{"edges":[[9,1],[9,2],[9,5],[9,6],[9,10],[9,11],[9,12],[9,13]],"s":9,"t":14,"weight":8},
{"edges":[[13,2],[13,4],[13,6],[13,8],[13,9],[13,11],[13,12],[13,14]],"s":13,"t":14,"weight":8}
]

{"nodes":[
    {"index":0,"nodeOffset":"2.5","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"57.66 -21.54","parent":[{"index":0}]},
    {"index":2,"nodeOffset":"60.01 -11.77","parent":[{"index":0},{"index":1}]},
    {"index":3,"nodeOffset":"57.21 2.64","parent":[{"index":0},{"index":1},{"index":2}]},
    {"index":4,"nodeOffset":"47.84 19.18","parent":[{"index":0},{"index":1},{"index":2},{"index":3}]},
    {"index":5,"nodeOffset":"31.58 35","parent":[{"index":0},{"index":1}]},
    {"index":6,"nodeOffset":"9.34 47.36","parent":[{"index":0},{"index":2},{"index":5}]},
    {"index":7,"nodeOffset":"-16.96 54.13","parent":[{"index":0},{"index":3},{"index":5},{"index":6}]},
    {"index":8,"nodeOffset":"-44.71 54.13","parent":[{"index":0},{"index":4},{"index":5},{"index":6},{"index":7}]},
    {"index":9,"nodeOffset":"14.7 22.36","parent":[{"index":1},{"index":2},{"index":5},{"index":6}]},
    {"index":10,"nodeOffset":"-10.71 10","parent":[{"index":1},{"index":3},{"index":5},{"index":7},{"index":9}]},
    {"index":11,"nodeOffset":"-30.14 -5.82","parent":[{"index":1},{"index":4},{"index":5},{"index":8},{"index":9},{"index":10}]},
    {"index":12,"nodeOffset":"-42.68 -22.36","parent":[{"index":2},{"index":3},{"index":6},{"index":7},{"index":9},{"index":10}]},
    {"index":13,"nodeOffset":"-48.66 -36.77","parent":[{"index":2},{"index":4},{"index":6},{"index":8},{"index":9},{"index":11},{"index":12}]},
    {"index":14,"nodeOffset":"-49.48 -46.54","parent":[{"index":3},{"index":4},{"index":7},{"index":8},{"index":10},{"index":11},{"index":12},{"index":13}]}
],
"config":{
    "algorithm":"Find edge cut Gomory-Hu",
    "maxIter":15000
}}

Sin embargo cuando el grafo tiene muchos más nodos y/o aristas el algoritmo no puede finalizar en un tiempo razonable. En la Figura vemos el grafo Johnson 8,4 con 70 vértices y 560 aristas sobre el que aplicamos getGomoryHuTree() con un máximo de 100 millones de iteraciones y no pudiendo finalizar. Se debe ejecutar en n-1 = 70-1 = 69 pasos, pudiendo sólo procesar los primeros debido al elevado número de vértices y aristas del grafo.

El algoritmo devuelve mensajes de error (findSTEdgeCut) Maximum iterations 100000000 reached al alcanzar las máximas iteraciones en casi 1 minuto llegando hasta sólo los 4 primeros nodos del total de 70 que tiene el grafo.

Time: 59929 ms 

Obtener árbol Gomory-Hu: {
"matrix":[],
"vertexTree":[[0],[1],[2],[3]],
"edgeTree":[[[4,8,5,6,7,10,9,11,13,12,14,24,17,15,16,18,21,19,20,22,23,29,25,26,27,30,28,31,32,33,34,54,42,36,35,37,38,41,39,40,44,43,49,45,46,47,50, 48,51,52,53,63,56,55,57,59,58,60,64,61,62,66,65,67,68,69],[0]],
    [[4,8,5,6,7,10,9,11,13,12,14,24,17,15,16,18,21,19,20,22,23,29,25,26,27,30,28,31,32,33,34,54,42,36,35,37,38,41,39,40,44,43,49,45,46,47,50,48,51,52,53,63,56,55,57,59,58,60,64,61,62,66,65,67,68,69],[1]],
    [[4,8,5,6,7,10,9,11,13,12,14,24,17,15,16,18,21,19,20,22,23,29,25,26,27,30,28,31,32,33,34,54,42,36,35,37,38,41,39,40,44,43,49,45,46,47,50,48,51,52,53,63,56,55,57,59,58,60,64,61,62,66,65,67,68,69],[2]],
    [[4,8,5,6,7,10,9,11,13,12,14,24,17,15,16,18,21,19,20,22,23,29,25,26,27,30,28,31,32,33,34,54,42,36,35,37,38,41,39,40,44,43,49,45,46,47,50,48,51,52,53,63,56,55,57,59,58,60,64,61,62,66,65,67,68,69],[3]]],
"weightTree":[],
"verification":[],
"warnings":["(findSTEdgeCut) Maximum iterations 100000000 reached"],
"trace":""}

Todos los algoritmos usan la matriz de adyacencia como estructura de datos del grafo. Y no siempre la matriz de adyacencia es la más eficiente, pues en la de este ejemplo hay 70 × 70 = 4900 valores, mientras que en la lista de aristas sólo hay 560 × 2 = 1120 valores. Como hay que copiar la matriz de adyacencia en cada uno de los n-1 = 69 pasos que necesita getGomoryHuTree(), si usáramos la lista de aristas ahorraríamos sólo en esto la copia de (4900-1120)×69 = 260820 valores.

Como siempre lo primero que tenemos que hacer con un algoritmo es que funcione, es decir, que sea eficaz. Y sólo después intentaremos además que sea eficiente, lo que es una tarea más compleja, pero que se facilita una vez entendemos su funcionamiento.

Por ejemplo, una de las opciones que vemos en la Figura es método para flujo, que tal como explicamos allí, puede ser "findPath", "dijkstra" o "floyd" usando por defecto "findPath" en todos los ejemplos anteriores. Este algoritmo getGomoryHuTree() usa findSTEdgeCut() que a su vez necesita un algoritmo para encontrar un camino entre dos nodos, usando por defecto el algoritmo findPath(), aunque pueden ser más eficientes los algoritmos "dijkstra" con getShortestPathDijkstra() o "floyd" con getShortestPathFloyd() que encuentran un camino mínimo entre dos nodos más eficientemente.

En la Figura vemos que usando "dijkstra" el algoritmo finaliza con menos de 10000 iteraciones y con un tiempo de ejecución de tan sólo 245 ms. No mostramos el resultado aquí para evitar exceso de datos, pero puede descargarlo en el archivo result.txt. Igualmente puede descargar el JSON para importar el ejemplo en el archivo json.txt

Verificar el resultado al obtener el árbol Gomory-Hu

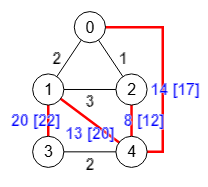
En las opciones del algoritmo getGomoryHuTree() que vimos en la Figura disponíamos de la opción verificar, cuyo cometido es chequear el resultado una vez obtenido.

Con el grafo de la Figura y marcando la opción para verificar, obtenemos el siguiente resultado:

Obtener árbol Gomory-Hu: {
"matrix":
[[0,0,0,0,17],
[0,0,0,22,20],
[0,0,0,0,12],
[0,22,0,0,0],
[17,20,12,0,0]],
"vertexTree":[0,2,3,4,1],
"edgeTree":[[0,4],[2,4],[1,3],[1,4]],
"weightTree":[17,12,22,20],
"verification":[true,[
    "Weight cut 0-4 ==  weightTree[0] ⇒ 17 == 17 ⇒ true",
    "Weight cut 2-4 ==  weightTree[1] ⇒ 12 == 12 ⇒ true",
    "Weight cut 1-3 ==  weightTree[2] ⇒ 22 == 22 ⇒ true",
    "Weight cut 1-4 ==  weightTree[3] ⇒ 20 == 20 ⇒ true"]
],
"warnings":[],
"trace":""}

El algoritmo devuelve las aristas [0,4], [2,4], [1,3], [1,4], llevándose a cabo la verificación al finalizar el algoritmo y antes de devolver el resultado, ejecutando findSTEdgeCut() entre cada pareja "u,v" de cada arista comprobando que el peso del corte mínimo coincide con el peso de la arista "u-v" en el árbol Gomory-Hu. Vemos que devuelve "true" inicial y luego lo mismo para cada "u,v", lo que nos sirve para identificar que parejas devuelven falso en caso de que suceda, algo que con los ejemplos que he probado no ha sucedido, pero esto me ha servido para ir depurando errores a medida que iba implementando el algoritmo getGomoryHuTree().

{"nodes":[
    {"index":0,"parent":[{"index":-1}]},
    {"index":1,"parent":[{"index":0,"value":2,"lineTextOffset":-0.8}]},
    {"index":2,"parent":[{"index":0,"value":1,"lineTextOffset":0.8},{"index":1,"value":3,"lineTextOffset":"0 0.8"}]},
    {"index":3,"parent":[{"index":1,"value":20,"lineTextOffset":-0.8},{"index":4,"value":2,"lineTextOffset":"0 0.8"}]},
    {"index":4,"parent":[{"index":1,"value":13,"lineTextOffset":"0 0.8"},{"index":2,"value":8,"lineTextOffset":0.8},{"index":0,"value":14,"lineOffset":"1","lineTextOffset":0.8}]}
],
"config":{
    "algorithm":"Get Gomory-Hu tree",
    "verify":true
}}

Nuevas aristas en árbol Gomory-Hu

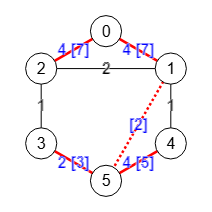
Hemos dicho quel árbol Gomory-Hu es de cubrimiento de todos los nodos y que las aristas pueden ser las existentes, como en los ejemplos de los primeros apartados, o bien originar nuevas aristas, como la arista "1-5" que vemos punteada para el grafo de la Figura.

Recordemos que un corte mínimo "s,t" se refiere a separar dos nodos "s" y "t" no necesariamente adyacentes en el grafo, así que las aristas del árbol Gomory-Hu no necesariamente han de existir en el grafo inicial.

Obtener árbol Gomory-Hu: {
"matrix":
[[0,7,7,0,0,0],
[7,0,0,0,0,2],
[7,0,0,0,0,0],
[0,0,0,0,0,3],
[0,0,0,0,0,5],
[0,2,0,3,5,0]],
"vertexTree":[0,2,1,3,5,4],
"edgeTree":[[0,1],[0,2],[1,5],[3,5],[4,5]],
"weightTree":[7,7,2,3,5],
"verification":[],
"warnings":[],
"trace":""}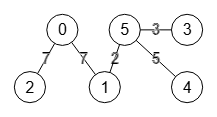

Importando en la aplicación la matriz de adyacencia obtenida veremos el árbol de la Figura, el mismo que el resaltado en la Figura.

0 7 7 0 0 0
7 0 0 0 0 2
7 0 0 0 0 0
0 0 0 0 0 3
0 0 0 0 0 5
0 2 0 3 5 0

{"nodes":[
    {"index":0,"nodeOffset":"-7.5","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"35.15 -10","parent":[{"index":0,"value":4}]},
    {"index":2,"nodeOffset":"-50.15 -10","parent":[{"index":0,"value":4},{"index":1,"value":2}]},
    {"index":3,"nodeOffset":"-16.81 -5","parent":[{"index":2,"value":1}]},
    {"index":4,"nodeOffset":"1.81 -5","parent":[{"index":1,"value":1}]},
    {"index":5,"nodeOffset":"-7.5 -15","parent":[{"index":3,"value":2},{"index":4,"value":4}]}
],
"config":{
    "algorithm":"Get Gomory-Hu tree"
}}

Árbol Gomory-Hu de un grafo árbol

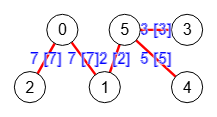
En el apartado anterior vimos un árbol Gomory-Hu, que aplicándole nuevamente el algoritmo getGomoryHuTree() observamos en la Figura que obtenemos el mismo árbol. Así que el árbol Gomory-Hu de un Gomory-Hu es el mismo Gomory-Hu.

Obtener árbol Gomory-Hu: {
"matrix":
[[0,7,7,0,0,0],
[7,0,0,0,0,2],
[7,0,0,0,0,0],
[0,0,0,0,0,3],
[0,0,0,0,0,5],
[0,2,0,3,5,0]],
"vertexTree":[0,2,1,3,5,4],
"edgeTree":[[0,1],[0,2],[1,5],[3,5],[4,5]],
"weightTree":[7,7,2,3,5],
"verification":[],
"warnings":[],
"trace":""}

{"nodes":[
    {"index":0,"nodeOffset":"0 -0.5","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"8.67 -2.5","parent":[{"index":0,"value":7}]},
    {"index":2,"nodeOffset":"-54.67 -2.5","parent":[{"index":0,"value":7}]},
    {"index":3,"nodeOffset":"25 -0.5","parent":[{"index":-1}]},
    {"index":4,"nodeOffset":"0 22.5","parent":[{"index":-1}]},
    {"index":5,"nodeOffset":"0 -50.5","parent":[{"index":1,"value":2},{"index":3,"value":3},{"index":4,"value":5}]}
],
"config":{
    "algorithm":"Get Gomory-Hu tree"
}}

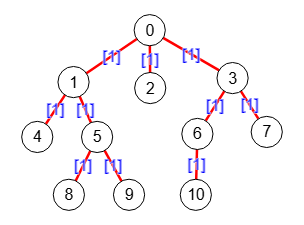
De hecho el árbol Gomory-Hu de cualquier árbol es el mismo árbol, como se observa en el de la Figura, grafo árbol sin pesos donde se consideran las aristas con peso unitario.

Obtener árbol Gomory-Hu: {
"matrix":
[[0,1,1,1,0,0,0,0,0,0,0],
[1,0,0,0,1,1,0,0,0,0,0],
[1,0,0,0,0,0,0,0,0,0,0],
[1,0,0,0,0,0,1,1,0,0,0],
[0,1,0,0,0,0,0,0,0,0,0],
[0,1,0,0,0,0,0,0,1,1,0],
[0,0,0,1,0,0,0,0,0,0,1],
[0,0,0,1,0,0,0,0,0,0,0],
[0,0,0,0,0,1,0,0,0,0,0],
[0,0,0,0,0,1,0,0,0,0,0],
[0,0,0,0,0,0,1,0,0,0,0]],
"vertexTree":[2,4,0,1,8,3,7,6,10,5,9],
"edgeTree":[[0,1],[0,2],[1,4],[0,3],[1,5],[3,6],[5,8],[3,7],[6,10],[5,9]],
"weightTree":[1,1,1,1,1,1,1,1,1,1],
"verification":[],
"warnings":[],
"trace":""}

{"nodes":[
    {"index":0,"nodeOffset":"10 -0.4","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"4.47 -4.6","parent":[{"index":0}]},
    {"index":2,"nodeOffset":"10.2 -2.2","parent":[{"index":0}]},
    {"index":3,"nodeOffset":"18.2 -6.2","parent":[{"index":0}]},
    {"index":4,"nodeOffset":"-5.07 -7.6","parent":[{"index":1}]},
    {"index":5,"nodeOffset":"-1.09 -7.6","parent":[{"index":1}]},
    {"index":6,"nodeOffset":"19.1 -8.8","parent":[{"index":3}]},
    {"index":7,"nodeOffset":"26.89 -9.6","parent":[{"index":3}]},
    {"index":8,"nodeOffset":"2.6 -9.4","parent":[{"index":5}]},
    {"index":9,"nodeOffset":"1.71 -9.4","parent":[{"index":5}]},
    {"index":10,"nodeOffset":"3.47 -9.4","parent":[{"index":6}]}
],
"config":{
    "algorithm":"Get Gomory-Hu tree"
}}

Árbol Gomory-Hu de un grafo completo

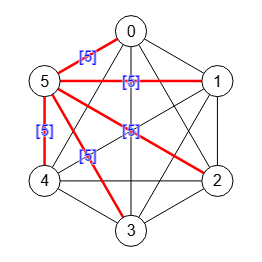
En la Figura vemos el árbol Gomory-Hu del grafo completo K6 con seis nodos, observando que el árbol Gomory-Hu de un grafo completo siempre es un grafo estrella con un nodo cualquiera en el centro, seleccionado el algoritmo getGomoryHuTree() el último.

Obtener árbol Gomory-Hu: {
"matrix":
[[0,0,0,0,0,5],
[0,0,0,0,0,5],
[0,0,0,0,0,5],
[0,0,0,0,0,5],
[0,0,0,0,0,5],
[5,5,5,5,5,0]],
"vertexTree":[0,1,2,3,5,4],
"edgeTree":[[0,5],[5,1],[5,2],[5,3],[5,4]],
"weightTree":[5,5,5,5,5],
"trace":"
,"warnings":[]}

{"nodes":[
    {"index":0,"nodeOffset":"2.5","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"70.47 -5","parent":[{"index":0}]},
    {"index":2,"nodeOffset":"53.81 35","parent":[{"index":0},{"index":1}]},
    {"index":3,"nodeOffset":"2.5 55","parent":[{"index":0},{"index":1},{"index":2}]},
    {"index":4,"nodeOffset":"-48.81 35","parent":[{"index":0},{"index":1},{"index":2},{"index":3}]},
    {"index":5,"nodeOffset":"-65.47 -5","parent":[{"index":0},{"index":1},{"index":2},{"index":3},{"index":4}]}
],
"config":{
    "algorithm":"Get Gomory-Hu tree"
}}

Vemos en la Figura el árbol Gomory-Hu importando desde la matriz de adyacencia del resultado obtenido.

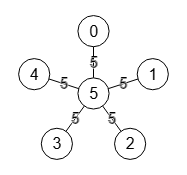
Aplicando un ajuste a círculo podemos presentarlo como un grafo estrella. Vea que alternando cada uno de los nodos en el centro hay n árboles Gomory-Hu para un grafo completo con n nodos si no tenemos en cuenta el ordenamiento de los restantes.

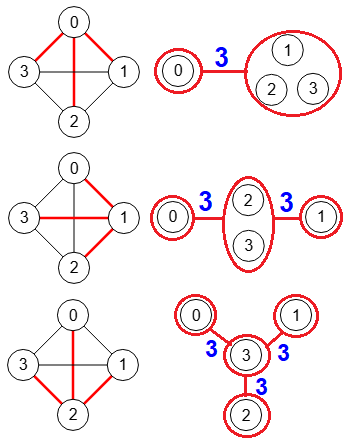
Para ver el mótivo del grafo estrella, en la Figura representamos los tres pasos del algoritmo getGomoryHuTree() para el grafo completo K4 con cuatro nodos.

En la traza resumida que se expone a continuación vemos que no se produce contracción de nodos de T en ningún caso, pues en cada paso va separando cada nodo, quedando el último en el centro de la estrella.

Step 1
vertexTree:[[0,1,2,3]]
Get subset:[0,1,2,3]
Set s=0, t=1 from subset
Get remainingVertexs:[]
Contract remainingVertexs:[]
componentsLabels:[[0],[1,2,3]]
vertexTree:[[0],[1,2,3]]
edgeTree:[[[0],[1,2,3]]]
weightTree:[3]
----------------------------------------
Step 2
vertexTree:[[0],[1,2,3]]
Get subset:[1,2,3]
Set s=1, t=2 from subset
Get remainingVertexs:[[0]]
Contract remainingVertexs:[]
componentsLabels:[[0,2,3],[1]]
vertexTree:[[0],[2,3],[1]]
edgeTree:[[[2,3],[0]],[[2,3],[1]]]
weightTree:[3,3]
----------------------------------------
Step 3
vertexTree:[[0],[2,3],[1]]
Get subset:[2,3]
Set s=2, t=3 from subset
Get remainingVertexs:[[0],[1]]
Contract remainingVertexs:[]
componentsLabels:[[0,1,3],[2]]
vertexTree:[[0],[1],[3],[2]]
edgeTree:[[[3],[0]],[[3],[1]],[[3],[2]]]
weightTree:[3,3,3]

Construir árbol Gomory-Hu getGomoryHuTree()