Las particiones también cuentan el número de esquemas de rimas de un poema. Entonces podemos generar B(n) particiones y por tanto rimas distintas. Si el conjunto de partida son n líneas de poemas (o versos) numeradas 1..n, podemos generar B(n) posibles formas de disponer las rimas en esas líneas.

Por ejemplo, con n=3 disponemos del conjunto de partida de líneas numeradas {1, 2, 3}, generándose las particiones 123, 12.3, 13.2, 1.23, 1.2.3 expresadas de forma compacta. Cada dígito representa la línea donde hemos de incluir una rima entre [A, B, C], que se van seleccionando en orden. Así una partición como 12.3 se traduce como AAB indicando que las 2 primeras líneas riman, pues están en el mismo subconjunto. Y la tercera no rima con ninguna al ser única en su subconjunto.

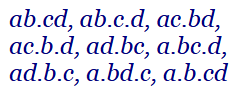
Las particiones con bloques parciales (o Bell parcial), que denominaremos pB(n, k), son las particiones de un conjunto con n elementos tal que alguno de los subconjuntos (o bloques) son de longitud igual a k. En la Figura vemos las particiones con bloques parciales de tamaño k=2 para un conjunto con n=4 elementos, donde cada partición contiene al menos un subconjunto o bloque de tamaño k=2.

Por otro lado las particiones con semi bloques parciales (o semi Bell), que denominaremos sB(n, k), son las particiones de un conjunto con n elementos tal que ninguno de los subconjuntos (o bloques) son de longitud igual a k. Por ejemplo, para el conjunto con n elementos {a, b, c} tenemos con k=1 la única partición abc expresada de forma compacta, donde ningún subconjunto o bloque tienen longitud unitaria; con k=2 tenemos abc, a.b.c; con k=3 tenemos ab.c, ac.b, a.bc, a.b.c; mientras que con k=0 o k>3 tenemos todas las particiones posibles abc, ab.c, ac.b, a.bc, a.b.c.

Un número de Stirling de segunda clase es el número de formas de particionar un conjunto de n elementos en k subconjuntos no vacíos, denotándose como S2(n, k).

Dado que un número de Stirling S2(n, k) es una partición de orden k-ésima, podemos contar todas las particiones de un conjunto de n elementos con B(n) = ∑_j=0..n S2(n, j)

En el primer algoritmo partition1(list) que vimos en el tema anterior necesitábamos las combinaciones y sus complementarias, lo que hacíamos usando dos veces el algoritmo combine2(list, k), una para las combinaciones y otra para las complementarias. Para evitar este doble coste ideamos el algoritmo combineComplement1(list, k) que nos permite obtener ambos resultados en una única ejecución, reduciendo significativamente el coste.

Una partición de un conjunto son los agrupamientos de sus elementos en subconjuntos no vacíos, de tal forma que cada elemento está incluido en un único subconjunto. En la imagen vemos las cinco particiones que se generan con el conjunto A = {a, b, c}. Por ejemplo, observando la segunda partición {{a, b}, {c}} se evidencia que la unión de estos subconjuntos {a, b} ⋃ {c} = A es el conjunto de partida. Y que la intersección es vacía {a, b} ⋂ {c} = ∅, que es lo mismo que decir que los subconjuntos son disjuntos.

Ya vimos en uno de los primeros temas que el número de combinaciones sin repetición de n elementos distintos en subconjuntos de k elementos son las posibles muestras de k elementos distintos y sin orden que pueden extraerse de los n elementos. El número de subconjuntos S de orden k que se obtienen son las combinaciones C(n, k).

Si partimos del conjunto A con n elementos y S_i,k designa uno de esos subconjuntos con 1 ≤ i ≤ C(n, k), entonces A - S_i,k es el subconjunto complementario de combinaciones. Todos los subconjuntos complementarios conforman entonces las combinaciones complementarias de orden k del conjunto A con n elementos.

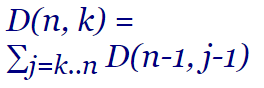
En este tema implementaremos un algoritmo para generar los desarreglos parciales usando la recurrencia D(n, k) = ∑_j=k..n D(n-1, j-1) que calcula su valor numérico, tal como vimos en el tema anterior.

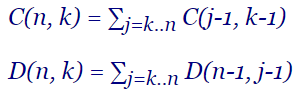
En temas anteriores hemos visto que el valor numérico de los desarreglos parciales se puede calcular con D(n, k) = C(n, k) × D(n-k) y también con D(n, k) = n/k D(n-1, k-1). En este tema buscaremos una tercera forma con similitud con la que ya habíamos visto para las combinaciones C(n, k) = ∑_j=k..n C(j-1, k-1), como se observa en la imagen, aplicando D(n, k) = ∑_j=k..n D(n-1, j-1)

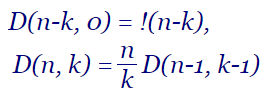
En el tema anterior vimos que la recurrencia D(n, k) = n/k D(n-1, k-1), como se observa en la imagen, también nos sirve para calcular el valor numérico de los desarreglos parciales. En este tema implementaremos un segundo algoritmo para generar los desarreglos parciales basándonos en esa recurrencia.

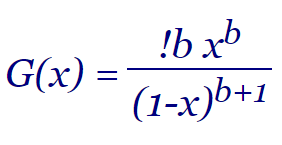
En el tema anterior vimos que el número de desarreglos parciales se calcula con la fórmula D(n, k) = C(n, k) × D(n-k, 0) donde D(n-k, 0) = !(n-k). En este tema vamos a deducir la fórmula recurrente D(n, k) = n/k D(n-1, k-1) para calcular también el valor numérico de los desarreglos parciales, pudiendo expresarse también con la función generadora G(x) = !b x^b / (1-x)^b+1.

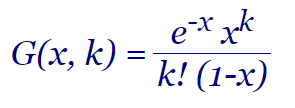
Los desarreglos parciales de una lista con n elementos distintos son todas las sublistas ordenadas con n elementos distintos que se pueden generar de tal forma que solo k elementos aparecen en su posición original. También se pueden definir como las permutaciones de n elementos con k puntos fijos. Las denotamos como D(n, k), correspondiendo con k=0 a los desarreglos sin puntos fijos que vimos en un tema anterior.

También se les denomina Rencontres numbers traducido como Problema de encuentros (o reencuentros). La función generadora de esta familia de funciones combinatorias es G(x, k) = e^-x x^k / (k! (1-x)). En este tema implementaremos un primer algoritmo para generar los desarreglos parciales.

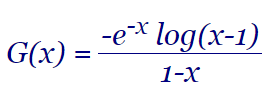
En un apartado del tema anterior que trataba sobre el coste de un algoritmo recursivo para generar desarreglos, habíamos llegado a una función sobre la que omitíamos obtener el término general en ese momento, pues contenía un logaritmo.

Era el producto de e^-x/(1-x) que genera los subfactoriales y del logaritmo log(x-1), función que hasta ahora no habíamos tratado de obtener su serie asociada y término general. En este tema analizaremos esto.

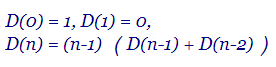
En este tema vamos a implementar un segundo algoritmo para generar los desarreglos de una lista con n elementos. Se basa en la primera recurrencia D(n) = (n-1) ( D(n-1) + D(n-2) ) que expusimos en un tema anterior.

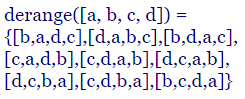
Los desarreglos (derangement) de una lista con n elementos distintos son todas las sublistas ordenadas con n elementos distintos que se pueden generar de tal forma que ninguno aparece en su posición original. Se denota como D(n). Y también como !n, el subfactorial de n.

Una permutación de n elementos tiene uno o más elementos que son puntos fijos si esos elementos se mantienen en su posición original. Desde esta definición un desarreglo es una permutación que no tiene ningún punto fijo.

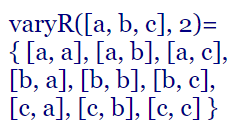
Las variaciones con repetición de una lista con n elementos distintos son todas las sublistas ordenadas con k elementos no necesariamente distintos que se pueden extraer. Su valor es VR(n, k) = n^k. En este tema veremos un algoritmo para obtener las permutaciones con repetición.