Arborescencia de mínimo coste en grafos
Arborescencia de mínimo coste sin especificar raíz
Vimos en el tema anterior los árboles de recubrimiento mínimo (MST Minimum Spanning Tree) con los algoritmos de Prim y Kruskal, árboles que sólo aplicaban a grafos no dirigidos. Para grafos dirigidos hablamos de arborescencia, que es un grafo dirigido con un nodo raíz donde desde esa raíz al resto de cada uno de los nodos sólo hay un único camino posible. Digamos que hablamos de árboles para no dirigidos y arborescencias con una raíz para dirigidos, pero en el fondo ambos son árboles. Si con árboles no dirigidos hablábamos de MST, para dirigidos a veces se les denomina DMST Directed Minimum Spanning Tree. Buscar una arborescencia de mínimo coste en un grafo dirigido supone encontrar aquella cuya suma de pesos sea mínima.
Para encontrar una arborescencia de mínimo coste sin especificar raíz aplicaremos un algoritmo del tipo voraz ordenándose las aristas por su peso creciente, iterando por ese orden seleccionando aquellas que cumplan ciertos criterios e irlas añadiendo al árbol final. En el siguiente apartado expondremos el JavaScript de este algoritmo getMinimumCostArborescenceNoRoot().
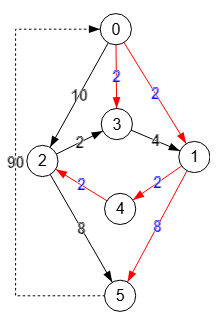
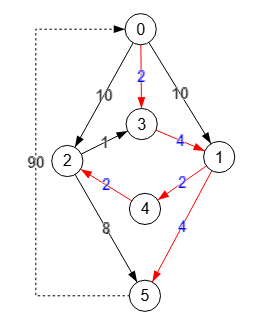
El grafo dirigido tiene que ser fuertemente conectado con objeto de asegurar que existe un camino entre cada par de nodos del grafo. Usamos el algoritmo convertToStronglyConnected() para convertir un grafo dirigido a fuertemente conectado si no lo fuera, agregándose una o más aristas tal como puede observarse en la Figura, pues ese grafo no es fuertemente conectado. La nueva arista "5🡒0" con peso 90 se resalta con línea de puntos, siendo su peso el resultado de multiplicar 10 × 9 pues el mayor peso de las aristas es 10 y hay 9 aristas, con lo que aseguramos que esa nueva arista no intervendrá en el algoritmo en caso de que exista otro camino de menor peso.
En este algoritmo no se especifica la raíz, pero al final la arborescencia obtenida tendrá un nodo raíz, que para el ejemplo de la Figura es el nodo 0. En la aplicación obtenemos el siguiente resultado con raíz "0" y suma de pesos 16.
Arborescencia de mínimo coste sin raíz: {
"edges":[[0,1],[0,3],[1,4],[4,2],[1,5]],
"weight":16,
"root":0,
"warnings":["Note: the graph is not strongly connected and the edges '5🡒0' are inserted with weight '90'"],
"newEdges":[[5,0,90]],
"trace":[]}Con este JSON puede importar el ejemplo.
{"nodes":[
{"index":0,"nodeOffset":"13.07 -0.8","parent":[{"index":1,"value":2},{"index":2,"value":10},{"index":3,"value":2}]},
{"index":1,"nodeOffset":"57.87 0.4","parent":[{"index":4,"value":2},{"index":5,"value":8}]},
{"index":2,"nodeOffset":"-23 2","parent":[{"index":3,"value":2},{"index":5,"value":8}]},
{"index":3,"nodeOffset":"-13.2 -12.8","parent":[{"index":1,"value":4}]},
{"index":4,"nodeOffset":"-31.87 21.2","parent":[{"index":2,"value":2}]},
{"index":5,"nodeOffset":"-18.56 106","parent":[{"index":-1}]}
],
"config":{
"markerEnd":"arrow",
"algorithm":"Minimum cost arborescence no root",
"lineTypeNewEdges":"rect -3.5"
}}Recordemos que en un algoritmo voraz se considera un conjunto de candidatos que se van analizando, tomando en cada iteración el que a corto plazo resulte más aceptable para conseguir la optimalidad que se espera del resultado final. Una vez seleccionado un candidato se incorpora al resultado, no reconsiderándose más adelante dicha decisión y permaneciendo en la solución hasta el final. Si por alguna razón no llegamos a un resultado óptimo no habrá forma de deshacer las acciones.
La arborescencia encontrada en el grafo de la Figura tiene un peso total 16 con las aristas [[0,1],[0,3],[1,4],[4,2],[1,5]]. Dada la simplicidad del grafo podemos encontrar una más [[0,1],[0,3],[1,4],[4,2],[2,5]] con peso total también 16 cambiando "1🡒5" por "2🡒5", pues ambas tienen el mismo peso. Vemos que ya no hay más y que en cualquier caso la de mínima arborescencia tiene peso total 16. En este caso el algoritmo encuentra la solución óptima, pero al ser un voraz no siempre la va a encontrar como veremos en el siguiente ejemplo.
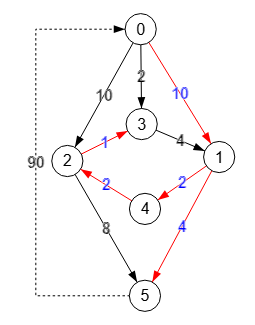
En la Figura vemos otro grafo parecido al anterior pero cambiando algunos pesos en aristas, obteniéndose la arborescencia [[2,3],[1,4],[4,2],[1,5],[0,1]] con suma de pesos 19, como observamos en el resultado obtenido a continuación, pero hay otro de menor peso 14 que es con las aristas [[0,3],[1,5],[1,4],[4,2],[3,1]]. Por lo tanto este algoritmo del tipo voraz no siempre consigue la arborescencia de mínimo coste, lo que parece que sucede cuando interviene un ciclo en la selección de aristas, algo que se resuelve con el algoritmo de Edmonds que veremos después. Veáse que el ciclo [1,4,2,3] en este caso interviene en la incorrecta selección de aristas por parte del algoritmo voraz, pues en lugar de seleccionar "0🡒1" y "2🡒3" con suma de pesos 10+1=11 debería seleccionar "0🡒3" y 3🡒1" con suma de pesos 2+4=6 inferior.
Arborescencia de mínimo coste sin raíz: {
"edges":[[2,3],[1,4],[4,2],[1,5],[0,1]],
"weight":19,
"root":0,
"warnings":["Note: the graph is not strongly connected and the edges '5🡒0' are inserted with weight '90'"],
"newEdges":[[5,0,90]],
trace:[]}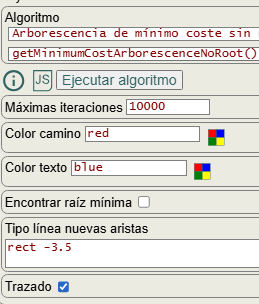
En la Figura vemos las opciones para obtener la arborescencia de mínimo coste sin especificar raíz. Las opciones color camino, color texto y tipo línea nuevas aristas no forman parte del algoritmo getMinimumCostArborescenceNoRoot() que veremos en un siguiente apartado y se usan posteriormente para resaltar aristas, textos de las aristas y nuevas aristas para hacer el grafo fuertemente conectado, como comentamos antes. La opción encontrar raíz mínima usará el algoritmo arborescencia de mínimo coste Edmonds que siempre encuentra una arborescencia de mínimo coste, como explicaremos en un siguiente apartado. Finalmente la opción trazado nos devuelve la siguiente traza si se activa para el segundo ejemplo de la Figura:
Edges sorted:, [[2,3,1],[0,3,2],[1,4,2],[4,2,2],[1,5,4],[3,1,4],[2,5,8],[0,1,10],[0,2,10],[5,0,90]], n-1 = 5 edges tree, Added [2,3,1], Discarded [0,3,2] because 3 already has an incoming edge [2,3,1], Added [1,4,2], Added [4,2,2], Added [1,5,4], Discarded [3,1,4] because forms cycle, Discarded [2,5,8] because 5 already has an incoming edge [1,5,4], Added [0,1,10], Ending with n-1=5 edges, Incoming edges [0,1,1,1,1,1] ⇒ root=0
La mayoría de los algoritmos de la aplicación usan como estructura de datos del grafo una matriz de adyacencia, que para este ejemplo se considera con pesos. Se obtienen las aristas con getEdges() con pesos, que son de la forma [u, v, w] siendo "u🡒v" la arista y "w" su peso. El primer paso es ordenarlas por su peso creciente, como vemos en Edges sorted. Un grafo fuertemente conectado con n nodos tendrá una arborescencia con n-1 aristas, que será el número de pasos que necesita el algoritmo para construir la arborescencia.
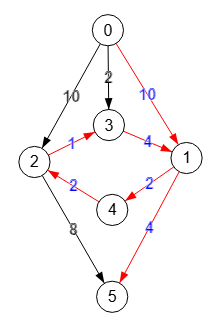
Tomamos la primera arista "2🡒3" y la agregamos al árbol. Vemos que ahora el nodo "3" tiene esa arista entrante. En una arborescencia cada nodo que no sea raíz sólo puede tener una arista entrante, aunque puede tener más salientes, o cero si es un nodo "hoja" (que está al final de una rama). Por eso descartamos la siguiente arista "0🡒3" pues el nodo "3" ya tiene una arista entrante.
Seguimos añadiendo aristas hasta que llegamos a "3🡒1", que descartamos pues formaría un ciclo con "1🡒4", "4🡒2" y "2🡒3" que hemos añadido previamente. Rercordamos que un árbol es un grafo no dirigido, conectado y sin ciclos, que también aplica en la arborescencia para un grafo dirigido no debiendo tener ciclos, pues entre el nodo raíz y cada uno del resto de nodos sólo hay un único camino posible, de tal forma que el ciclo "1🡒4🡒2🡒3🡒1" tiene que "romperse" en alguna arista entrante a alguno de los nodos "1,4,2,3" con objeto de que en ese nodo permita vincular otra arista entrante del resto del grafo pues en otro caso tendría dos aristas entrantes y habrían dos caminos para llegar a ese nodo. En la Figura vemos el ciclo "1🡒4🡒2🡒3🡒1", observando que para llegar al nodo "1" desde la raíz tenemos el camino "0🡒1" y otro alternativo "0🡒1🡒4🡒2🡒3🡒1" que incluye el ciclo. Descartando la arista "3🡒1" solventamos este problema.
También se descarta "2🡒5" pues "5" ya tiene una entrante añadida previamente. Cuando tenemos 5 aristas en la arborescencia finalizamos. Si contamos las aristas entrantes en cada nodo de la arborescencia veremos que todos tiene una menos la raíz que no tiene ninguna, deduciéndose esa raíz con Incoming edges [0,1,1,1,1,1] ⇒ root=0. Observe que la arista entrante al nodo raíz "0" es la que hemos agregado "5🡒0" con peso 90 para hacer el grafo fuertemente conectado, pero que no será seleccionada pues se encuentra al final de las aristas ordenadas por pesos
Con este JSON puede importar ese ejemplo.
{"nodes":[
{"index":0,"nodeOffset":"23.07 -0.8","parent":[{"index":1,"value":10},{"index":2,"value":10},{"index":3,"value":2}]},
{"index":1,"nodeOffset":"67.87 0.4","parent":[{"index":4,"value":2},{"index":5,"value":4}]},
{"index":2,"nodeOffset":"-13 2","parent":[{"index":3,"value":1},{"index":5,"value":8}]},
{"index":3,"nodeOffset":"-3.2 -12.8","parent":[{"index":1,"value":4}]},
{"index":4,"nodeOffset":"-21.87 21.2","parent":[{"index":2,"value":2}]},
{"index":5,"nodeOffset":"-8.56 106","parent":[{"index":-1}]}
],
"config":{
"markerEnd":"arrow",
"algorithm":"Minimum cost arborescence no root",
"lineTypeNewEdges":"rect -3.5",
"tracing":true
}}
Si en las opciones que vimos en la Figura marcamos la opción encontrar raíz mínima, el algoritmo no utilizará el voraz que hemos explicado antes, sino el algoritmo de arborescencia de mínimo coste de Edmonds que veremos en un apartado siguiente. Este algoritmo siempre encuentra la arborescencia de coste mínimo, observando en la Figura y en la traza siguiente que encuentra una con peso 14, cuando la encontrada con el voraz tenía peso 19.
Se observa en la traza que iteramos por todos los nodos para actuar como raíz. Obviamente como el nodo "0" no tiene inicialmente aristas entrantes y le hemos adjudicado la nueva arista "5🡒0" con peso 90, la mínima arborescencia es la primera con raíz en ese nodo "0" con suma de pesos 14 que no incluye la arista "5🡒0", pues el resto si la incluyen y la suma de pesos supera 90.
Arborescencia de mínimo coste sin raíz: {
"edges":[[0,3],[1,5],[1,4],[4,2],[3,1]],
"weight":14,
"root":0,
"warnings":["Note: the graph is not strongly connected and the edges '5🡒0' are inserted with weight '90'"],
"newEdges":[[5,0,90]],
trace:[
Run getMinimumCostArborescenceEdmonds() with root from 0 to 5,
Root: 0, weight: 14, edges: [[0,3],[1,5],[1,4],[4,2],[3,1]],
Root: 1, weight: 99, edges: [[1,4],[1,5],[2,3],[4,2],[5,0]],
Root: 2, weight: 101, edges: [[1,4],[1,5],[2,3],[3,1],[5,0]],
Root: 3, weight: 102, edges: [[1,4],[1,5],[3,1],[4,2],[5,0]],
Root: 4, weight: 101, edges: [[1,5],[2,3],[3,1],[4,2],[5,0]],
Root: 5, weight: 100, edges: [[0,3],[1,4],[4,2],[3,1],[5,0]]"]}Algoritmo getMinimumCostArborescenceNoRoot()
El JavaScript para ejecutar getMinimumCostArborescenceNoRoot() del apartado anterior se muestra a continuación. Usa los siguientes algoritmos:
isGraphDirected()para saber si el grafo es dirigido, pues el algoritmo sólo aplica a dirigidos.isGraphConnected()para saber si el grafo es fuertemente conectado.convertToStronglyConnected()que, en caso de no ser fuertemente conectado, se realiza esta conversión.getEdges()para obtener las aristas desde la matriz de adyacencia de entrada al algoritmo que recibimos en el argumentomatrix.hasCycles()para saber si un grafo tiene ciclos.getMinimumCostArborescenceEdmonds()para obtener la arborescencia de coste mínimo con el algoritmo de Edmonds, que veremos en el siguiente apartado.
En el código prescindimos de la parte destinada a devolver la traza.
function getMinimumCostArborescenceNoRoot({matrix=[], findMinRoot=false}){
let result = {edges: [], weight: 0, root: 0, warnings: [], newEdges: []}, temp;
try {
let n = matrix.length;
if (temp = isGraphDirected({matrix}), typeof temp==="string") throw new Error(temp);
if (!temp) throw new Error(`The graph is undirected and the minimum cost arborescence cannot be obtained`);
if (temp = isGraphConnected({matrix}), typeof temp==="string") throw new Error(temp);
let connected = temp;
if (!connected) {
if (temp = convertToStronglyConnected({matrix}), typeof temp==="string") throw new Error(temp);
result.newEdges = temp.newEdges;
let weightBig = result.newEdges[0][2];
let nedges = result.newEdges.map(v => `${v[0]}🡒${v[1]}`).join(", ");
result.warnings.push(`Note: the graph is not strongly connected and the edges '${nedges}' are inserted with weight '${weightBig}'`);
}
if (!findMinRoot) {
if (temp = getEdges({matrix, edgesCompact:true, weights:true}), typeof temp==="string") throw new Error(temp);
let edges = temp.toSorted((v,w) => v[2]-w[2]);
let matrixTree = Array.from({length:n}, () => Array.from({length:n} , () => 0));
for (let edge of edges) {
let [i, j, w] = edge;
let k = result.edges.findIndex(v => v[1]===j);
if (k===-1) {
matrixTree[i][j] = w;
if (temp = hasCycles({matrix:matrixTree, ignoreSelfLoops:true, directed:true}), typeof temp==="string") throw new Error(temp);
if (temp) {
matrixTree[i][j] = 0;
} else {
result.edges.push([i,j,w]);
if (result.edges.length===n-1) break;
}
}
}
result.weight = result.edges.reduce((p,v) => (p+=v[2], p), 0);
result.edges = result.edges.map(v => [v[0], v[1]]);
let numberIncomingEdges = Array.from({length: n}, () => 0);
for (let [i, j] of result.edges.values()) {
numberIncomingEdges[j]++;
}
result.root = numberIncomingEdges.findIndex(v => v===0);
} else {
let minEdges = [];
let minWeight = Infinity;
let minRoot = -1;
for (let root=0; root<n; root++) {
iter = 0;
if (temp = getMinimumCostArborescenceEdmonds({matrix, root}), typeof temp==="string") throw new Error(temp);
let edges = temp.edges;
let weight = temp.weight;
if (weight<minWeight) {
minWeight = weight;
minEdges = edges;
minRoot = root;
}
}
result.edges = minEdges;
result.weight = minWeight;
result.root = minRoot;
}
} catch(e) {result = e.message}
return result;
}En el argumento findMinRoot recibimos la opción encontrar raíz mínima que vimos entre las opciones de la Figura. Antes de if (!findMinRoot) el algoritmo observa si el grafo recibido en la matriz de adyacencia matrix es dirigido, pues sólo aplica a dirigidos. Si no es fuertemente conectado se fuerza a ello. El primer bloque que se ejecuta cuando findMinRoot es falso contiene el algoritmo voraz que hemos explicado más arriba. Recordamos el esquema de código de un algoritmo voraz:
Function greedy(set){
result = create(set);
while (not isSolution(result) && not isEmpty(set)){
candidate = select(set);
if (isFeasible(result, candidate)) {
result = save(result, candidate);
}
}
return result;
}El conjunto set en nuestro algoritmo es la lista de aristas edges donde una arista es como [u, v, w] correspondiéndose con la arista dirigida "u🡒v" con peso "w". En set iteraremos para obtener las aristas de la arborescencia. El resultado result en nuestro algoritmo es result.edges donde iremos guardando las aristas de la arborescencia. Se comprueba si el resultado es solución con isSolution(result), lo que sucede cuando tengamos n-1 aristas con un grafo con n nodos. Recordemos que un grafo con n nodos dirigido y fuertemente conectado debe tener como mínimo n aristas, con lo que su arborescencia tendrá n-1 aristas dado que una de ellas hará que se forme un ciclo pues al ser fuertemente conectado es posible un camino entre dos nodos cualesquiera. Así que la cuestión isEmpty(set) que observa si ya no quedan aristas en el conjunto set para completar el resultado no es necesaria, pues siempre habrán suficientes para completar esa arborescencia en tanto que el grafo es fuertemente conectado.
La función select(set) que selecciona un candidato (candidate) no es necesaria pues el conjunto de aristas en set ya nos viene ordenado creciente por pesos y al iterar por ellas iremos tomando primero las de menor peso. La función isFeasible(result, candidate) observa si ese candidato es completable o factible, que para nuestro caso supone ver que la incorporación de esa arista no forma un ciclo o que no exista otra arista entrante en el mismo nodo en la arborescencia que estamos construyendo. Ya expusimos ejemplos sobre esto más arriba. Si es completable o factible guardamos esa arista en el resultado, algo que en el esquema anterior expresamos como result = save(result, candidate).
El esquema del voraz anterior es básico y su implementación dependerá de cada caso. Así por ejemplo en lugar de un bucle while usamos un for saliendo del bucle con un break cuando tengamos n-1 aristas en la arborescencia. A continuación mostramos la parte del voraz reduciendo código con puntos suspensivos y agregando comentarios para relacionarlo con el esquema anterior. Vemos que las aristas de la arborescencia las vamos guardando en result.edges, pero además necesitamos una matriz de adyacencia matrixTree para esa arborescencia, puesto que usaremos el algoritmo hasCycles() para saber si un grafo tiene ciclos. Recordemos que la mayoría de los algoritmos en la aplicación usan la matriz de adyacencia como estructura de datos. Si no encontramos una arista anterior agregada al grafo con esa misma arista entrante, que se comprueba con result.edges.findIndex(v => v[1]===j) vemos si esa arista agregada a la matriz matrixTree no contiene un ciclo. Si lo contiene quitamos esa arista de esa matriz y pasamos a la siguiente.
let result = {edges: [], weight: 0, root: 0, ...; // result = create(set);
...
if (temp = getEdges({matrix, edgesCompact:true, weights:true}), ...;
let edges = temp.toSorted((v,w) => v[2]-w[2]); // candidates ordered by increasing weight
let matrixTree = Array.from({length:n}, () => Array.from({length:n} , () => 0));
for (let edge of edges) { // while
let [i, j, w] = edge; // candidate = select(set)
let k = result.edges.findIndex(v => v[1]===j); // if (isFeasible(result, candidate))
if (k===-1) {
matrixTree[i][j] = w;
if (temp = hasCycles({matrix:matrixTree, ignoreSelfLoops:true, directed:true}), ...;
if (temp) {
matrixTree[i][j] = 0;
} else {
// result = save(result, candidate);
result.edges.push([i,j,w]);
if (result.edges.length===n-1) break; // isSolution(result)
}
}
}
result.weight = result.edges.reduce((p,v) => (p+=v[2], p), 0);
result.edges = result.edges.map(v => [v[0], v[1]]);
let numberIncomingEdges = Array.from({length: n}, () => 0);
for (let [i, j] of result.edges.values()) {
numberIncomingEdges[j]++;
}
result.root = numberIncomingEdges.findIndex(v => v===0);La segunda parte del algoritmo es para el caso de que la opción encontrar raíz mínima sea verdadera, que nos viene en el argumento findMinRoot. Contiene un bucle que itera por los n nodos del grafo designándolos como raíces y aplicando el algoritmo getMinimumCostArborescenceEdmonds() que veremos en un apartado siguiente. Vamos guardando la arborescencia de menor peso pues al final será la que se devuelve. Reproducimos nuevamente esta parte del algoritmo:
let result = {edges: [], ...;
....
let minEdges = [];
let minWeight = Infinity;
let minRoot = -1;
for (let root=0; root<n; root++) {
iter = 0;
if (temp = getMinimumCostArborescenceEdmonds({matrix, root}), ...;
let edges = temp.edges;
let weight = temp.weight;
if (weight<minWeight) {
minWeight = weight;
minEdges = edges;
minRoot = root;
}
}
result.edges = minEdges;
result.weight = minWeight;
result.root = minRoot;Arborescencia de mínimo coste Edmonds
El algoritmo de Edmonds encuentra siempre una arborescencia de coste mínimo en un grafo dirigido especificando un nodo raíz y siempre que exista un camino entre esa raíz y cada uno de los nodos restantes. Ahora no es necesario que el grafo sea fuertemente conectado como en el algoritmo del apartado anterior. Si seleccionamos una raíz donde no se pueda acceder a todos los nodos, este algoritmo nos advertirá del error y no se ejecutará.
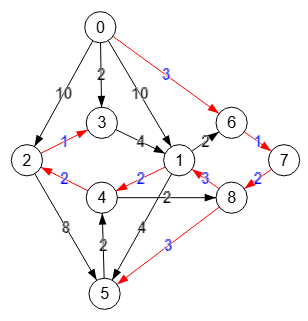
Este algoritmo de Edmonds es más fácil de explicar que de implementar. Quizás es mejor exponer unos ejemplos para ver su funcionamiento y al final explicar la implementación que he llevado a cabo en JavaScript y que se expone en getMinimumCostArborescenceEdmonds() en el apartado siguiente. En primer lugar tenemos el grafo de la Figura, un grafo dirigido sin ciclos. Como dijimos, en este algoritmo hay que designar necesariamente un nodo raíz, revisando el algoritmo que podemos acceder desde esa raíz al resto de nodos.
En el grafo de la Figura la única raíz posible es el nodo "0". Este algoritmo de Edmonds siempre encuentra una arborescencia de coste mínimo, a diferencia del voraz que vimos en el apartado anterior que no siempre consigue la solución óptima. Habremos de tener en cuenta también que pueden haber más de una arborescencia con el mismo coste mínimo. En el ejemplo vemos que se devuelven las aristas [0,1],[0,2],[1,4],[1,5],[2,3] con suma de pesos 10+10+2+4+1=27. Pero también es posible [0,1],[0,2],[1,4],[2,5],[2,3] con el mismo peso. O [0,1],[0,2],[3,2],[2,5],[2,3] tambien con el mismo peso. Recordando que en un árbol sólo puede haber una arista entrante en cada nodo (menos la raíz que en algún caso como este puede no entrar ninguna), vea que los nodos "4" y "5" tienen dos aristas entrantes de igual peso, con lo que seleccionar cualquier combinación de ellas sirve para mantener el mismo peso total.
Con este JSON puede importar el ejemplo de la Figura.
{"nodes":[
{"index":0,"nodeOffset":"13.07 -50.8","parent":[{"index":1,"value":10},{"index":2,"value":10},{"index":3,"value":2}]},
{"index":1,"nodeOffset":"44.54 25.4","parent":[{"index":4,"value":2},{"index":5,"value":4}]},
{"index":2,"nodeOffset":"-49.67 2","parent":[{"index":3,"value":1},{"index":5,"value":4}]},
{"index":3,"nodeOffset":"-19.87 12.2","parent":[{"index":4,"value":2}]},
{"index":4,"nodeOffset":"14.8 71.2","parent":[{"index":-1}]},
{"index":5,"nodeOffset":"-18.56 106","parent":[{"index":-1}]}
],
"config":{
"markerEnd":"arrow",
"algorithm":"Minimum cost arborescence Edmonds",
"tracing":true
}}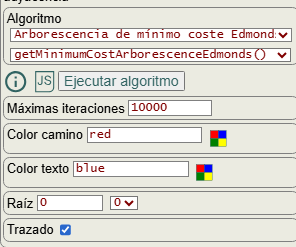
En la Figura vemos las opciones para ejecutar el algoritmo de Edmonds, con la opción raíz para seleccionar el nodo raíz. Las opciones color camino y color texto no se pasan al algoritmo y sirven para, posteriormente a su ejecución, resaltar las aristas y textos que forman la arborescencia. Con la opción trazado marcada nos devuelve la siguiente traza para el ejemplo anterior, donde observamos una fase de contracción (contraction phase) y otra fase de expansión (expansion phase). En un grafo sin ciclos no hay fase de expansión.
Arborescencia de mínimo coste Edmonds: {
"edges":[[0,1],[0,2],[1,4],[1,5],[2,3]],
"weight":27,
"warnings":[],
trace:[
CONTRACTION PHASE,
k = 0,
Edges previous: [[0,1,10],[0,2,10],[0,3,2],[1,4,2],[1,5,4],[2,3,1],[2,5,4],[3,4,2]],
Vertexs: [0,1,2,3,4,5],
Labels: [[0],[1],[2],[3],[4],[5]],
Root: 0,
Edges min: [[0,1,0],[0,2,0],[0,3,1],[1,4,0],[1,5,0],[2,3,0],[2,5,0],[3,4,0]],
Edges zero: [[0,1],[0,2],[1,4],[1,5],[2,3]],
Is arborescence: true,
Edges tree: [[0,1],[0,2],[1,4],[1,5],[2,3]],
EXPANSION PHASE"]}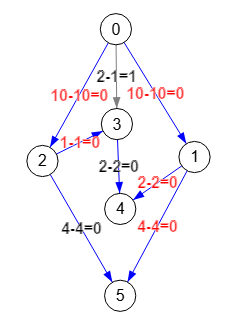
Hay un bucle interno que itera desde k=0. En esta primera situación tenemos en Edges previous las aristas iniciales con pesos del grafo, recordando que una entrada como [u, v, w] designa la arista "u🡒v" con peso "w". En Vertexs tenemos los vértices iniciales [0,1,2,3,4,5]. Y en Labels tenemos las etiquetas iniciales [[0],[1],[2],[3],[4],[5]], algo que entenderemos mejor su uso cuando veamos el ejemplo con contraccion de ciclos. Por ahora digamos que si no hay ciclos no hay nada que contraer.
En cada paso construimos las aristas cero que guardamos en Edges zero. Para ello iteramos por cada nodo menos la raíz restando a los pesos de las aristas previas entrantes Edges previous a ese nodo el peso de la arista de menor peso, con lo que obtenemos las aristas mínimas Edges min: [[0,1,0], [0,2,0], [0,3,1], [1,4,0], [1,5,0], [2,3,0], [2,5,0], [3,4,0]] desde la cual filtraremos las de peso cero en Edges zero tal como explicamos a continuación.
En cada paso almacenamos las instancias actuales de Edges min y Labels pues las necesitaremos en la fase de expansión, aunque no para este ejemplo pues no es necesaria. También almacenamos Vertexs que, aunque no necesaria en la fase de expansión, nos servirá para visualizarlas en el trazado. En Edges tree tenemos una única instancia que vamos actualizando, pues esa variable contendrá finalmente la arborescencia.
Vertex Incoming Weigth Minimum Rest
edges Weight
---------------------------------------------
1 0🡒1 10 10 10-10=0
2 0🡒2 10 10 10-10=0
3 0🡒3 2 1 2-1=1
2🡒3 1 1 1-1=0
4 1🡒4 2 2 2-2=0
3🡒4 2 2 2-2=0
5 1🡒5 4 4 4-4=0
2🡒5 4 4 4-4=0En la Figura vemos las aristas entrantes en cada vértice con peso final cero resaltadas en azul, pasando a formar parte de Edges zero las que tienen el texto rojo. El esquema adjunto muestra que iteramos por los vértices observando sus aristas entrantes Edges para obtener las aristas mínimas Edge min y de ellas seleccionar las aristas cero Edges zero. Por ejemplo, al nodo "3" entran dos aristas: "0🡒3" con peso 2 y "2🡒3" con peso 1, restando ese menor peso 1 de ambas nos queda la primera con peso 1 y la segunda con peso 0 que es la que se selecciona en aristas cero. Cuando hay dos o más aristas entrantes con peso cero se selecciona la primera que se encuentre. Así sucede con los vértices "4" y "5".
Al final tendremos las aristas cero Edges zero: [[0,1],[0,2],[1,4],[1,5],[2,3]]. Y estas aristas forman claramente una arborescencia con la raíz "0" como se observa en la Figura con las aristas de etiquetas con color rojo, que son las mismas que vemos en la Figura, con lo que habremos finalizado el algoritmo devolviendo esas aristas como arborescencia de mínimo coste.
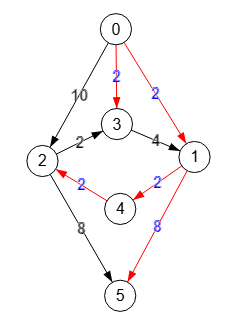
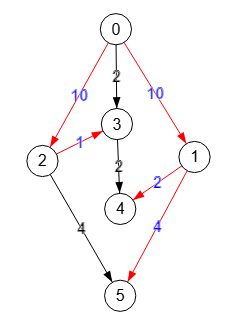
En la Figura vemos otro grafo que contiene el ciclo "1🡒4🡒2🡒3🡒1", pero que ese ciclo no será necesario contraerlo, como veremos a continuación. El primer paso siempre es obtener las aristas cero Edges zero:
Vertex Incoming Weigth Minimum Rest
edges Weight
---------------------------------------------
1 0🡒1 2 2 2-2=0
3🡒1 4 2 4-2=2
2 0🡒2 10 2 10-2=8
4🡒2 2 2 2-2=0
3 0🡒3 2 2 2-2=0
2🡒3 2 2 2-2=0
4 1🡒4 2 2 2-2=0
5 1🡒5 8 8 8-8=0
2🡒5 8 8 8-8=0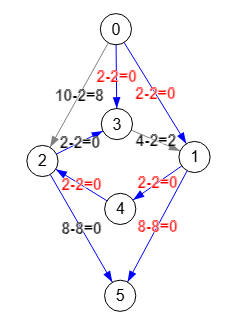
Realizando el mismo proceso que explicamos antes, en la Figura vemos las aristas cero en color azul, de las cuáles se seleccionan las que tienen texto rojo, observando que forman una arborescencia, con lo que con este paso finalizamos el algoritmo. Vemos que el grafo inicial tiene un ciclo, pero al construir las aristas cero ese ciclo desaparece.
A continuación mostramos la traza que devuelve el algoritmo, con la arborescencia [[0,1],[0,3],[1,4],[1,5],[4,2]] que son las aristas azules con texto rojo de la Figura y que también vemos resaltadas en la Figura.
Arborescencia de mínimo coste Edmonds: {
"edges":[[0,1],[0,3],[1,4],[1,5],[4,2]],
"weight":16,
"warnings":[],
trace:[
CONTRACTION PHASE,
k = 0,
Edges previous: [[0,1,2],[0,2,10],[0,3,2],[1,4,2],[1,5,8],[2,3,2],[2,5,8],[3,1,4],[4,2,2]],
Vertexs: [0,1,2,3,4,5],
Labels: [[0],[1],[2],[3],[4],[5]],
Root: 0,
Edges min: [[0,1,0],[0,2,8],[0,3,0],[1,4,0],[1,5,0],[2,3,0],[2,5,0],[3,1,2],[4,2,0]],
Edges zero: [[0,1],[0,3],[1,4],[1,5],[4,2]],
Is arborescence: true,
Edges tree: [[0,1],[0,3],[1,4],[1,5],[4,2]],
EXPANSION PHASE"]}Con este JSON puede importar el ejemplo.
{"nodes":[
{"index":0,"nodeOffset":"13.07 -0.8","parent":[{"index":1,"value":2},{"index":2,"value":10},{"index":3,"value":2}]},
{"index":1,"nodeOffset":"57.87 0.4","parent":[{"index":4,"value":2},{"index":5,"value":8}]},
{"index":2,"nodeOffset":"-23 2","parent":[{"index":3,"value":2},{"index":5,"value":8}]},
{"index":3,"nodeOffset":"-13.2 -12.8","parent":[{"index":1,"value":4}]},
{"index":4,"nodeOffset":"-31.87 21.2","parent":[{"index":2,"value":2}]},
{"index":5,"nodeOffset":"-18.56 106","parent":[{"index":-1}]}
],
"config":{
"markerEnd":"arrow",
"algorithm":"Minimum cost arborescence Edmonds",
"tracing":true
}}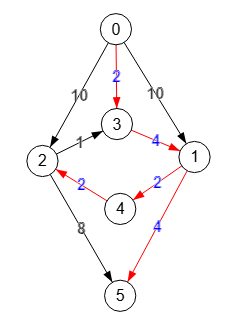
En la Figura vemos otro grafo con el mismo ciclo "1🡒4🡒2🡒3🡒1" como el anterior pero con otro peso en la arista "2🡒3", ciclo que simplemente expresamos como [1,4,2,3], donde ahora si que se mantiene en las aristas zero, que como siempre, es lo primero que tenemos que obtener:
Vertex Incoming Weigth Minimum Rest
edges Weight
---------------------------------------------
1 0🡒1 10 4 10-4=6
3🡒1 4 4 4-4=0
2 0🡒2 10 2 10-2=8
4🡒2 2 2 2-2=0
3 0🡒3 2 1 2-1=1
2🡒3 1 1 1-1=0
4 1🡒4 2 2 2-2=0
5 1🡒5 4 4 4-4=0
2🡒5 8 4 8-4=4
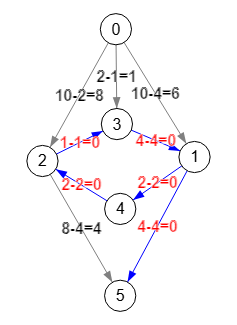
Vemos en la Figura que esas aristas cero [[1,4],[1,5],[2,3],[3,1],[4,2]] no forman una arborescencia, pues además de no incluir el nodo "0" se observa que se mantiene el ciclo [1,4,2,3]. Y ahora es cuando realmente empieza la complejidad del algoritmo, pues cada vez que aparezca un ciclo en las aristas cero hay que contraerlo.
En la traza siguiente observamos que se detecta ese ciclo y se contrae, pasando entonces a la segunda iteración k=1, cuya entrada Edges ya incluye la contracción del ciclo [1,4,2,3].
Arborescencia de mínimo coste Edmonds: {
"edges":[[0,3],[1,4],[1,5],[3,1],[4,2]],
"weight":14,
"warnings":[],
trace:[
CONTRACTION PHASE,
k = 0,
Edges previous: [[0,1,10],[0,2,10],[0,3,2],[1,4,2],[1,5,4],[2,3,1],[2,5,8],[3,1,4],[4,2,2]],
Vertexs: [0,1,2,3,4,5],
Labels: [[0],[1],[2],[3],[4],[5]],
Root: 0,
Edges min: [[0,1,6],[0,2,8],[0,3,1],[1,4,0],[1,5,0],[2,3,0],[2,5,4],[3,1,0],[4,2,0]],
Edges zero: [[1,4],[1,5],[2,3],[3,1],[4,2]],
Is arborescence: false,
Cycle: [1,4,2,3] ⇒ contract,
k = 1,
Edges previous: [[0,1,6],[0,1,8],[0,1,1],[1,5,0],[1,5,4]],
Vertexs: [0,1,5],
Labels: [[0],[1,4,2,3],[5]],
Root: 0,
Edges min: [[0,1,5],[0,1,7],[0,1,0],[1,5,0],[1,5,4]],
Edges zero: [[0,1],[1,5]],
Is arborescence: true,
Edges tree: [[0,1],[1,5]],
EXPANSION PHASE,
k = 1,
Edges tree previous: [[0,1],[1,5]],
Edges min [k-1]: [[0,1,6],[0,2,8],[0,3,1],[1,4,0],[1,5,0],[2,3,0],[2,5,4],[3,1,0],[4,2,0]],
Vertexs [k-1]: [0,1,2,3,4,5],
Labels [k]: [[0],[1,4,2,3],[5]],
Cycle: [1,4,2,3],
In cycle [0,1] ∈ Edges tree ⇒ [0,-1] ∈ Labels[k] ⇒ u=0 ⇒ Minimum in Edges min [k-1]: [0,3,1],
Vertex in cycle = 3,
Out cycle [1,5] ∈ Edges tree ⇒ [-1,5] ∈ Labels[k] ⇒ v=5 ⇒ Minimum in Edges min [k-1]: [1,5,0],
Edges tree in/out cycle: [[0,3],[1,5]],
(+) Edges tree inner cycle: [[0,3],[1,5],[1,4],[4,2],[3,1]],
(+) Edges tree rest: [[0,3],[1,5],[1,4],[4,2],[3,1]]"]}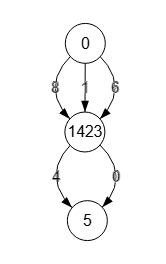
Un ciclo como [1,4,2,3] siempre lo ponemos en forma normalizada donde lo ordenamos con el vértice más pequeño al principio, recordando que se debe mantener la secuencia "1🡒4🡒2🡒3", con lo que podríamos ordenarla como [4,2,3,1], [2,3,1,4], [3,1,4,2] y [1,4,2,3], siendo esta última la que usaremos, pues el primer vértice "1" será el que identifique el nodo en la contracción. Entonces la contracción supone agrupar los vértices "1", "4", "2" y "3" en un nuevo nodo que etiquetamos con "1". En la Figura vemos la contracción que resulta al representar en un grafo las aristas Edges previous: [[0,1,6],[0,1,8],[0,1,1],[1,5,0],[1,5,4]] que vemos resaltadas en la traza anterior, en el nuevo paso k=1 de la fase de contracción.
Vemos en la traza los nuevos vértices Vertexs: [0,1,5] y las nuevas etiquetas Labels: [[0],[1,4,2,3],[5]] que nos permiten identificar los números de los vértices del paso anterior. Observe que el nuevo vértice "1" es el menor del ciclo [1,4,2,3] como dijimos antes. Los pesos de las aristas entrantes y salientes al nodo contraído son las obtenidas previamente en aristas mínimas (Edges min).
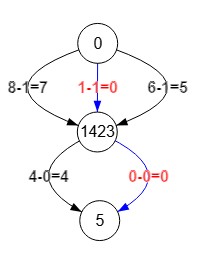
En el nuevo paso partiendo de las aristas del grafo anterior contraido de la Figura, obtenemos las aristas mínimas en Edges min: [[0,1,5],[0,1,7],[0,1,0],[1,5,0],[1,5,4]] de donde seleccionamos las aristas cero resultando Edges zero: [[0,1],[1,5]], viendo en la Figura que ahora forman una arborescencia. Hemos finalizado la fase de contracción y ahora sólo queda deshacer las contracciones que haremos en la fase de expansión que vimos en la traza anterior y que volvemos a reproducir nuevamente:
EXPANSION PHASE,
k = 1,
Edges tree previous: [[0,1],[1,5]],
Edges min [k-1]: [[0,1,6],[0,2,8],[0,3,1],[1,4,0],[1,5,0],[2,3,0],[2,5,4],[3,1,0],[4,2,0]],
Vertexs [k-1]: [0,1,2,3,4,5],
Labels [k]: [[0],[1,4,2,3],[5]],
Cycle: [1,4,2,3],
In cycle [0,1] ∈ Edges tree ⇒ [0,-1] ∈ Labels[k] ⇒ u=0 ⇒ Minimum in Edges min [k-1]: [0,3,1],
Vertex in cycle = 3,
Out cycle [1,5] ∈ Edges tree ⇒ [-1,5] ∈ Labels[k] ⇒ v=5 ⇒ Minimum in Edges min [k-1]: [1,5,0],
Edges tree in/out cycle: [[0,3],[1,5]],
(+) Edges tree inner cycle: [[0,3],[1,5],[1,4],[4,2],[3,1]],
(+) Edges tree rest: [[0,3],[1,5],[1,4],[4,2],[3,1]]En la fase de contracción iterábamos k=0, k=1 y ahora en la expansión empezamos desde el último k hasta k=1. Como sólo hubo una única contracción sólo habrá un paso de expansión con k=1. La última arborescencia que obtuvimos la vemos ahora en Edges tree previous: [[0,1],[1,5]]. Recuperamos las aristas con pesos mínimos del paso anterior Edges min [k-1]: [[0,1,6], [0,2,8], [0,3,1], [1,4,0], [1,5,0], [2,3,0], [2,5,4], [3,1,0], [4,2,0]]. También se exponen los vértices del paso k-1, aunque no se necesitarán en la fase de expansión. Lo que si necesitamos son las etiquetas del paso k siendo Labels[k]: [[0],[1,4,2,3],[5]]. De esas etiquetas recuperamos el ciclo [1,4,2,3] simplemente observando una posición que tenga más de un vértice.
En cada iteración descendente de la fase de expansión se ejecutan estos tres pasos:
- Seleccionar aristas entrantes y salientes al ciclo: Buscamos en la arborescencia
Edges tree previous: [[0,1],[1,5]]aristas [u, v] tal que "u" no esté en el ciclo y "v" esté en el ciclo [1,4,2,3], con lo que serán las aristas entrantes. Y al revés para las salientes. Para la primera arista [0,1] deEdges Tree previousvemos que encontramos [0] en las etiquetasLabels[k]: [[0],[1,4,2,3],[5]]pero no encontramos [1]. Así que [0,1] es una arista entrante al ciclo. Buscamos en las aristas mínimas del paso anteriorEdges min [k-1]: [[0,1,6], [0,2,8], [0,3,1], [1,4,0], [1,5,0], [2,3,0], [2,5,4], [3,1,0], [4,2,0]]aristas con u=0 siendo [0,1,6], [0,2,8] y [0,3,1], siendo la de menor peso [0,3,1] con lo que [0,3] pasa a ser la primera arista de la nueva arborescencia. La siguiente arista enEdges Tree previouses [1,5] encontrando [5] en las etiquetas pero no encontrando [1], siendo entonces [1,5] una arista saliente del ciclo. Buscamos aristas con v=5 enEdges min [k-1]resultando [1,5,0] y [2,5,4], siendo la de menor peso [1,5] que es la que agregamos a la arborescencia. - Seleccionar aristas interiores del ciclo: Como hemos identificado el ciclo [1,4,2,3] a partir de la posición con más de un vértice en las etiquetas
Labels[k]: [[0],[1,4,2,3],[5]], como dijimos antes, podemos construir las aristas que conforman ese ciclo "1🡒4", "4🡒2", "2🡒3", "3🡒1". Como en el paso anterior ya obtuvimos la arista entrante final [0,3] entonces el nodo "3" no puede tener más aristas entrantes, con lo que desecharemos la arista "2🡒3" e incorporamos a la arborescencia el resto [1,4], [4,2] y [3,1]. Con esto rompemos el ciclo. Observe en la traza que al seleccionar [0,3] identificamosVertex in cycle = 3con lo que ya sabemos que el vértice "3" tiene una arista entrante y, por tanto, desechamos la arista "2🡒3". - Incorporar resto de aristas no relacionadas con las anteriores: Aunque en este ejemplo no hay este tipo de aristas, se refiere a incorporar a la arborescencia el resto de aristas "u🡒v" de
Edges[k-1]donde "v" no tenga previamente ya una arista incidente. Son aristas externas al ciclo.
El resultado de la arborescencia en este paso es [[0,3], [1,5], [1,4], [4,2], [3,1]]. Como no hay más pasos de expansión habremos finalizado con esta arborescencia de peso mínimo. Si hubieran más pasos, esta sería la nueva Edges tree previous para el siguiente paso.
Con este JSON puede importar el ejemplo.
{"nodes":[
{"index":0,"nodeOffset":"13.07 -0.8","parent":[{"index":1,"value":10},{"index":2,"value":10},{"index":3,"value":2}]},
{"index":1,"nodeOffset":"57.87 0.4","parent":[{"index":4,"value":2},{"index":5,"value":4}]},
{"index":2,"nodeOffset":"-23 2","parent":[{"index":3,"value":1},{"index":5,"value":8}]},
{"index":3,"nodeOffset":"-13.2 -12.8","parent":[{"index":1,"value":4}]},
{"index":4,"nodeOffset":"-31.87 21.2","parent":[{"index":2,"value":2}]},
{"index":5,"nodeOffset":"-18.56 106","parent":[{"index":-1}]}
],
"config":{
"markerEnd":"arrow",
"algorithm":"Minimum cost arborescence Edmonds",
"tracing":true
}}
En la Figura vemos un grafo que es la modificación del ejemplo anterior agregando más nodos y aristas para formar más ciclos. Se producen tres contracciones, lo que servirá para analizar el comportamiento, especialmente en la fase de expansión.
Time: 0 ms
Arborescencia de mínimo coste Edmonds: {
"edges":[[0,6],[1,4],[2,3],[4,2],[6,7],[7,8],[8,1],[8,5]],
"weight":17,
"warnings":[],
trace:[
CONTRACTION PHASE,
k = 0,
Edges previous: [[0,1,10],[0,2,10],[0,3,2],[0,6,3],[1,4,2],[1,5,4],[1,6,2],[2,3,1],[2,5,8],[3,1,4],[4,2,2],[4,8,2],[5,4,2],[6,7,1],[7,8,2],[8,1,3],[8,5,3]],
Vertexs: [0,1,2,3,4,5,6,7,8],
Labels: [[0],[1],[2],[3],[4],[5],[6],[7],[8]],
Root: 0,
Edges min: [[0,1,7],[0,2,8],[0,3,1],[0,6,1],[1,4,0],[1,5,1],[1,6,0],[2,3,0],[2,5,5],[3,1,1],[4,2,0],[4,8,0],[5,4,0],[6,7,0],[7,8,0],[8,1,0],[8,5,0]],
Edges zero: [[1,4],[1,6],[2,3],[4,2],[4,8],[6,7],[8,1],[8,5]],
Is arborescence: false,
Cycle: [1,4,8] ⇒ contract,
k = 1,
Edges previous: [[0,1,7],[0,2,8],[0,3,1],[0,6,1],[1,5,1],[1,6,0],[2,3,0],[2,5,5],[3,1,1],[1,2,0],[5,1,0],[6,7,0],[7,1,0],[1,5,0]],
Vertexs: [0,1,2,3,5,6,7],
Labels: [[0],[1,4,8],[2],[3],[5],[6],[7]],
Root: 0,
Edges min: [[0,1,7],[0,2,8],[0,3,1],[0,6,1],[1,5,1],[1,6,0],[2,3,0],[2,5,5],[3,1,1],[1,2,0],[5,1,0],[6,7,0],[7,1,0],[1,5,0]],
Edges zero: [[1,6],[2,3],[1,2],[5,1],[6,7],[1,5]],
Is arborescence: false,
Cycle: [1,5] ⇒ contract,
k = 2,
Edges previous: [[0,1,7],[0,2,8],[0,3,1],[0,6,1],[1,6,0],[2,3,0],[2,1,5],[3,1,1],[1,2,0],[6,7,0],[7,1,0]],
Vertexs: [0,1,2,3,6,7],
Labels: [[0],[1,5],[2],[3],[6],[7]],
Root: 0,
Edges min: [[0,1,7],[0,2,8],[0,3,1],[0,6,1],[1,6,0],[2,3,0],[2,1,5],[3,1,1],[1,2,0],[6,7,0],[7,1,0]],
Edges zero: [[1,6],[2,3],[1,2],[6,7],[7,1]],
Is arborescence: false,
Cycle: [1,6,7] ⇒ contract,
k = 3,
Edges previous: [[0,1,7],[0,2,8],[0,3,1],[0,1,1],[2,3,0],[2,1,5],[3,1,1],[1,2,0]],
Vertexs: [0,1,2,3],
Labels: [[0],[1,6,7],[2],[3]],
Root: 0,
Edges min: [[0,1,6],[0,2,8],[0,3,1],[0,1,0],[2,3,0],[2,1,4],[3,1,0],[1,2,0]],
Edges zero: [[0,1],[2,3],[1,2]],
Is arborescence: true,
Edges tree: [[0,1],[2,3],[1,2]],
EXPANSION PHASE,
k = 3,
Edges tree previous: [[0,1],[2,3],[1,2]],
Edges min [k-1]: [[0,1,7],[0,2,8],[0,3,1],[0,6,1],[1,6,0],[2,3,0],[2,1,5],[3,1,1],[1,2,0],[6,7,0],[7,1,0]],
Vertexs [k-1]: [0,1,2,3,6,7],
Labels [k]: [[0],[1,6,7],[2],[3]],
Cycle: [1,6,7],
In cycle [0,1] ∈ Edges tree ⇒ [0,-1] ∈ Labels[k] ⇒ u=0 ⇒ Minimum in Edges min [k-1]: [0,6,1],
Vertex in cycle = 6,
No in/out cycle [2,3] ∈ Edges tree ⇒ [2,3] ∈ Labels[k],
Out cycle [1,2] ∈ Edges tree ⇒ [-1,2] ∈ Labels[k] ⇒ v=2 ⇒ Minimum in Edges min [k-1]: [1,2,0],
Edges tree in/out cycle: [[0,6],[1,2]],
(+) Edges tree inner cycle: [[0,6],[1,2],[6,7],[7,1]],
(+) Edges tree rest: [[0,6],[1,2],[6,7],[7,1],[2,3]],
k = 2,
Edges tree previous: [[0,6],[1,2],[6,7],[7,1],[2,3]],
Edges min [k-1]: [[0,1,7],[0,2,8],[0,3,1],[0,6,1],[1,5,1],[1,6,0],[2,3,0],[2,5,5],[3,1,1],[1,2,0],[5,1,0],[6,7,0],[7,1,0],[1,5,0]],
Vertexs [k-1]: [0,1,2,3,5,6,7],
Labels [k]: [[0],[1,5],[2],[3],[6],[7]],
Cycle: [1,5],
No in/out cycle [0,6] ∈ Edges tree ⇒ [0,4] ∈ Labels[k],
Out cycle [1,2] ∈ Edges tree ⇒ [-1,2] ∈ Labels[k] ⇒ v=2 ⇒ Minimum in Edges min [k-1]: [1,2,0],
No in/out cycle [6,7] ∈ Edges tree ⇒ [4,5] ∈ Labels[k],
In cycle [7,1] ∈ Edges tree ⇒ [7,-1] ∈ Labels[k] ⇒ u=7 ⇒ Minimum in Edges min [k-1]: [7,1,0],
Vertex in cycle = 1,
No in/out cycle [2,3] ∈ Edges tree ⇒ [2,3] ∈ Labels[k],
Edges tree in/out cycle: [[1,2],[7,1]],
(+) Edges tree inner cycle: [[1,2],[7,1],[1,5]],
(+) Edges tree rest: [[1,2],[7,1],[1,5],[0,6],[6,7],[2,3]],
k = 1,
Edges tree previous: [[1,2],[7,1],[1,5],[0,6],[6,7],[2,3]],
Edges min [k-1]: [[0,1,7],[0,2,8],[0,3,1],[0,6,1],[1,4,0],[1,5,1],[1,6,0],[2,3,0],[2,5,5],[3,1,1],[4,2,0],[4,8,0],[5,4,0],[6,7,0],[7,8,0],[8,1,0],[8,5,0]],
Vertexs [k-1]: [0,1,2,3,4,5,6,7,8],
Labels [k]: [[0],[1,4,8],[2],[3],[5],[6],[7]],
Cycle: [1,4,8],
Out cycle [1,2] ∈ Edges tree ⇒ [-1,2] ∈ Labels[k] ⇒ v=2 ⇒ Minimum in Edges min [k-1]: [4,2,0],
In cycle [7,1] ∈ Edges tree ⇒ [7,-1] ∈ Labels[k] ⇒ u=7 ⇒ Minimum in Edges min [k-1]: [7,8,0],
Vertex in cycle = 8,
Out cycle [1,5] ∈ Edges tree ⇒ [-1,5] ∈ Labels[k] ⇒ v=5 ⇒ Minimum in Edges min [k-1]: [8,5,0],
No in/out cycle [0,6] ∈ Edges tree ⇒ [0,5] ∈ Labels[k],
No in/out cycle [6,7] ∈ Edges tree ⇒ [5,6] ∈ Labels[k],
No in/out cycle [2,3] ∈ Edges tree ⇒ [2,3] ∈ Labels[k],
Edges tree in/out cycle: [[4,2],[7,8],[8,5]],
(+) Edges tree inner cycle: [[4,2],[7,8],[8,5],[1,4],[8,1]],
(+) Edges tree rest: [[4,2],[7,8],[8,5],[1,4],[8,1],[0,6],[6,7],[2,3]]"]}
{"nodes":[
{"index":0,"nodeOffset":"1.4 -0.8","parent":[{"index":-1},{"index":1,"value":10},{"index":2,"value":10},{"index":3,"value":2},{"index":6,"value":3}]},
{"index":1,"nodeOffset":"66.33 2.5","parent":[{"index":4,"value":2},{"index":5,"value":4},{"index":6,"value":2}]},
{"index":2,"nodeOffset":"-11.33 2.5","parent":[{"index":3,"value":1},{"index":5,"value":8}]},
{"index":3,"nodeOffset":"2 -12.5","parent":[{"index":1,"value":4}]},
{"index":4,"nodeOffset":"-14.67 17.5","parent":[{"index":2,"value":2},{"index":8,"value":2}]},
{"index":5,"nodeOffset":"19.78 81","parent":[{"index":4,"value":2}]},
{"index":6,"nodeOffset":"20.67 -12.5","parent":[{"index":7,"value":1}]},
{"index":7,"nodeOffset":"75 -22.5","parent":[{"index":8,"value":2}]},
{"index":8,"nodeOffset":"37.33 42.5","parent":[{"index":1,"value":3},{"index":5,"value":3}]}
],
"config":{
"markerEnd":"arrow",
"algorithm":"Minimum cost arborescence Edmonds",
"tracing":true
}}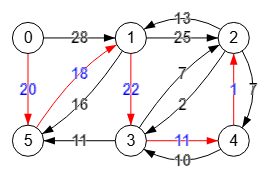
Para el ejemplo de la Figura con nuestra aplicación obtenemos la arborescencia [[0,5],[1,3],[3,4],[4,2],[5,1]] con peso total 72.
Ponemos este ejemplo pues con el algoritmo de Edmonds que implementamos se necesitan 4 contracciones, sirviendo para observar la fase de contracción y la de expansión en un ejemplo con más pasos.
En un PDF que vemos en Internet Minimum cost spanning r-arborescence de Giovanni Righini aparece el ejemplo de la Figura. En ese documento encuentra otra arborescencia [[0,5],[1,2],[2,3],[2,4],[5,1]] con el mismo peso total 20+25+2+7+18=72. Habla el documento sobre el algoritmo de Edmonds pero parece que aplica un algoritmo de ascenso dual (o primal-dual) (Dual ascent algorithm), algo que por ahora no he estudiado. Por lo visto si tenemos un problema primal y su dual relacionado, si encontrar la solución es más eficiente en el dual podemos resolverlo con el dual pues la solución óptima es la misma para ambas versiones.
Time: 1 ms
Arborescencia de mínimo coste Edmonds: {
"edges":[[0,5],[1,3],[3,4],[4,2],[5,1]],
"weight":72,
"warnings":[],
trace:[
CONTRACTION PHASE,
k = 0,
Edges previous: [[0,1,28],[0,5,20],[1,2,25],[1,3,22],[1,5,16],[2,1,13],[2,3,2],[2,4,7],[3,2,7],[3,4,11],[3,5,11],[4,2,1],[4,3,10],[5,1,18]],
Vertexs: [0,1,2,3,4,5],
Labels: [[0],[1],[2],[3],[4],[5]],
Root: 0,
Edges min: [[0,1,15],[0,5,9],[1,2,24],[1,3,20],[1,5,5],[2,1,0],[2,3,0],[2,4,0],[3,2,6],[3,4,4],[3,5,0],[4,2,0],[4,3,8],[5,1,5]],
Edges zero: [[2,1],[2,3],[2,4],[3,5],[4,2]],
Is arborescence: false,
Cycle: [2,4] ⇒ contract,
k = 1,
Edges previous: [[0,1,15],[0,5,9],[1,2,24],[1,3,20],[1,5,5],[2,1,0],[2,3,0],[3,2,6],[3,2,4],[3,5,0],[2,3,8],[5,1,5]],
Vertexs: [0,1,2,3,5],
Labels: [[0],[1],[2,4],[3],[5]],
Root: 0,
Edges min: [[0,1,15],[0,5,9],[1,2,20],[1,3,20],[1,5,5],[2,1,0],[2,3,0],[3,2,2],[3,2,0],[3,5,0],[2,3,8],[5,1,5]],
Edges zero: [[2,1],[2,3],[3,2],[3,5]],
Is arborescence: false,
Cycle: [2,3] ⇒ contract,
k = 2,
Edges previous: [[0,1,15],[0,5,9],[1,2,20],[1,2,20],[1,5,5],[2,1,0],[2,5,0],[5,1,5]],
Vertexs: [0,1,2,5],
Labels: [[0],[1],[2,3],[5]],
Root: 0,
Edges min: [[0,1,15],[0,5,9],[1,2,0],[1,2,0],[1,5,5],[2,1,0],[2,5,0],[5,1,5]],
Edges zero: [[1,2],[2,1],[2,5]],
Is arborescence: false,
Cycle: [1,2] ⇒ contract,
k = 3,
Edges previous: [[0,1,15],[0,5,9],[1,5,5],[1,5,0],[5,1,5]],
Vertexs: [0,1,5],
Labels: [[0],[1,2],[5]],
Root: 0,
Edges min: [[0,1,10],[0,5,9],[1,5,5],[1,5,0],[5,1,0]],
Edges zero: [[1,5],[5,1]],
Is arborescence: false,
Cycle: [1,5] ⇒ contract,
k = 4,
Edges previous: [[0,1,10],[0,1,9]],
Vertexs: [0,1],
Labels: [[0],[1,5]],
Root: 0,
Edges min: [[0,1,1],[0,1,0]],
Edges zero: [[0,1]],
Is arborescence: true,
Edges tree: [[0,1]],
EXPANSION PHASE,
k = 4,
Edges tree previous: [[0,1]],
Edges min [k-1]: [[0,1,15],[0,5,9],[1,5,5],[1,5,0],[5,1,5]],
Vertexs [k-1]: [0,1,5],
Labels [k]: [[0],[1,5]],
Cycle: [1,5],
In cycle [0,1] ∈ Edges tree ⇒ [0,-1] ∈ Labels[k] ⇒ u=0 ⇒ Minimum in Edges min [k-1]: [0,5,9],
Vertex in cycle = 5,
Edges tree in/out cycle: [[0,5]],
(+) Edges tree inner cycle: [[0,5],[5,1]],
(+) Edges tree rest: [[0,5],[5,1]],
k = 3,
Edges tree previous: [[0,5],[5,1]],
Edges min [k-1]: [[0,1,15],[0,5,9],[1,2,20],[1,2,20],[1,5,5],[2,1,0],[2,5,0],[5,1,5]],
Vertexs [k-1]: [0,1,2,5],
Labels [k]: [[0],[1,2],[5]],
Cycle: [1,2],
No in/out cycle [0,5] ∈ Edges tree ⇒ [0,2] ∈ Labels[k],
In cycle [5,1] ∈ Edges tree ⇒ [5,-1] ∈ Labels[k] ⇒ u=5 ⇒ Minimum in Edges min [k-1]: [5,1,5],
Vertex in cycle = 1,
Edges tree in/out cycle: [[5,1]],
(+) Edges tree inner cycle: [[5,1],[1,2]],
(+) Edges tree rest: [[5,1],[1,2],[0,5]],
k = 2,
Edges tree previous: [[5,1],[1,2],[0,5]],
Edges min [k-1]: [[0,1,15],[0,5,9],[1,2,24],[1,3,20],[1,5,5],[2,1,0],[2,3,0],[3,2,6],[3,2,4],[3,5,0],[2,3,8],[5,1,5]],
Vertexs [k-1]: [0,1,2,3,5],
Labels [k]: [[0],[1],[2,3],[5]],
Cycle: [2,3],
No in/out cycle [5,1] ∈ Edges tree ⇒ [3,1] ∈ Labels[k],
In cycle [1,2] ∈ Edges tree ⇒ [1,-1] ∈ Labels[k] ⇒ u=1 ⇒ Minimum in Edges min [k-1]: [1,3,20],
Vertex in cycle = 3,
No in/out cycle [0,5] ∈ Edges tree ⇒ [0,3] ∈ Labels[k],
Edges tree in/out cycle: [[1,3]],
(+) Edges tree inner cycle: [[1,3],[3,2]],
(+) Edges tree rest: [[1,3],[3,2],[5,1],[0,5]],
k = 1,
Edges tree previous: [[1,3],[3,2],[5,1],[0,5]],
Edges min [k-1]: [[0,1,15],[0,5,9],[1,2,24],[1,3,20],[1,5,5],[2,1,0],[2,3,0],[2,4,0],[3,2,6],[3,4,4],[3,5,0],[4,2,0],[4,3,8],[5,1,5]],
Vertexs [k-1]: [0,1,2,3,4,5],
Labels [k]: [[0],[1],[2,4],[3],[5]],
Cycle: [2,4],
No in/out cycle [1,3] ∈ Edges tree ⇒ [1,3] ∈ Labels[k],
In cycle [3,2] ∈ Edges tree ⇒ [3,-1] ∈ Labels[k] ⇒ u=3 ⇒ Minimum in Edges min [k-1]: [3,4,4],
Vertex in cycle = 4,
No in/out cycle [5,1] ∈ Edges tree ⇒ [4,1] ∈ Labels[k],
No in/out cycle [0,5] ∈ Edges tree ⇒ [0,4] ∈ Labels[k],
Edges tree in/out cycle: [[3,4]],
(+) Edges tree inner cycle: [[3,4],[4,2]],
(+) Edges tree rest: [[3,4],[4,2],[1,3],[5,1],[0,5]]"]}Con este JSON puede importar el ejemplo
{"nodes":[
{"index":0,"nodeOffset":"4.58 8.75","parent":[{"index":-1},{"index":1,"value":28},{"index":5,"value":20}]},
{"index":1,"nodeOffset":"29.17 8.75","parent":[{"index":2,"value":25},{"index":3,"value":22},{"index":5,"lineType":"quadratic","lineOffset":"0 2","value":16}]},
{"index":2,"nodeOffset":"53.75 8.75","parent":[{"index":3,"lineType":"quadratic","lineOffset":"0 2","value":2},{"index":4,"lineType":"quadratic","lineOffset":2.5,"value":7},{"index":1,"lineType":"quadratic","lineOffset":"0 -2.5","value":13}]},
{"index":3,"nodeOffset":"12.5 25","parent":[{"index":5,"value":11},{"index":4,"value":11},{"index":2,"lineType":"quadratic","lineOffset":"0 -2","value":7}]},
{"index":4,"nodeOffset":"37.08 50","parent":[{"index":2,"value":1},{"index":3,"lineType":"quadratic","lineOffset":"0 2.5","value":10}]},
{"index":5,"nodeOffset":"-62.08 50","parent":[{"index":1,"lineType":"quadratic","lineOffset":"0 -2","value":18}]}
],
"config":{
"markerEnd":"arrow",
"algorithm":"Minimum cost arborescence Edmonds",
"tracing":true
}}Algoritmo getMinimumCostArborescenceEdmonds()
A continuación mostramos el JavaScript de la implementación del algoritmo de Edmonds. Al inicio hay algunas sentencias que comprueban que la raíz está entre los nodos permitidos, que el grafo es dirigido con isGraphDirected() pues solo aplicará a grafos dirigidos y si hay un camino entre la raíz y el resto de los nodos, lo que hacemos con findPath(), pues en otro caso no se ejecutará el algoritmo.
A partir de aquí encontramos unas funciones internas, sobre las que hemos abreviado el código con puntos suspensivos "..." y que expondremos después. El resto es el cuerpo central del algoritmo, con unas declaraciones de variables, un bucle while de la fase de contracción y un bucle for de la fase de expansión, donde también suprimimos el código que expondremos después.
function getMinimumCostArborescenceEdmonds({matrix=[], root=0}){
let result = {edges: [], weight: 0, warnings: []}, temp;
try {
let n = matrix.length;
if (!(root>-1 && root<n)) throw new Error(`Root is wrong`);
if (temp = isGraphDirected({matrix}), typeof temp==="string") throw new Error(temp);
if (!temp) throw new Error(`The graph is undirected and the minimum cost arborescence cannot be obtained`);
for (let i=0; i<n; i++) {
if (i!==root) {
if (temp = findPath({matrix, firstIndex:root, lastIndex:i}), typeof temp==="string") throw new Error(temp);
if (temp.length===0) throw new Error(`Some nodes cannot be accessed from the root '${root}'`)
}
}
function getMatrix(edges=[], vertexs=[]) {...}
function isDST(matrix=[], root=0, labels=[]) {...}
function getMinInEdges(edges=[], vertexs=[], root=0) {...}
function getEdgesZero(edges=[]) {...}
function getCycle(matrix=[], vertexs=[]){...}
function contract(edges=[], cycle=[], root=0) {...}
if (temp = getEdges({matrix, edgesCompact:true, weights:true}), typeof temp==="string") throw new Error(temp);
let edges = temp;
let vertexs = Array.from({length:n}, (v,i) => i);
let labels = Array.from({length:n}, (v,i) => [i]);
let edgesItems = [edges];
let vertexsItems = [vertexs];
let labelsItems = [labels];
let edgesTree = [];
let k = 0;
// Contraction phase
while (edgesTree.length===0) {
...
}
// Expansion phase
for (let k=edgesItems.length-1; k>0; k--){
...
}
result.edges = edgesTree.toSorted((u,v) => u[0]===v[0] ? u[1]-v[1] : u[0]-v[0]);
result.weight = edgesTree.reduce((p,v) => (p+=matrix[v[0]][v[1]], p), 0);
} catch(e) {result = e.message}
return result;
}El pseudo-código de esta implementación se expone a continuación:
Algoritmo de Edmonds aristas = lista de aristas con pesos // edges, como [u, v, w] para arista u🡒v con peso w vértices = [v0, v1, ..., vn-1] // vertexs etiquetas = [[v0], [v1], ..., [vn-1]] // labels lista aristas = [aristas] // edgesItem lista vértices = [vértices] // vertexsItem lista etiquetas = [etiquetas] // labelsItem arborescencia = [] // edgesTree // Fase de contracción Mientras arborescencia sea vacía hacer aristas mínimas = obtener aristas mínimas desde aristas anteriores // getMinInEdges() aristas cero = filtrar aristas mínimas con peso cero // getEdgesZero() Si aristas cero es una arborescencia entonces // isDST() arborescencia = aristas cero En otro caso ciclo = obtener ciclo desde aristas cero // getCycle() aristas, vértices, etiquetas = contraer ciclo en aristas mínimas // contract() agregar aristas de este paso en lista aristas agregar vértices de este paso en lista vértices agregar etiquetas de este paso en lista etiquetas Fin si Fin Mientras // Fase de expansión Para k=última aristas de la lista hasta k=1 hacer aristas = lista aristas k-1 // edges = edgesItem[k-1] etiquetas = lista etiquetas k // labels = labelsItem[k] ciclo = recuperar ciclo desde etiquetas // labels.filter(v => v.length>1)[0] nueva arborescencia = [] // newEdgesTree resto aristas = [] // restEdges vértice entrada ciclo = null // vertexInCycle // Seleccionar aristas entrantes y salientes al ciclo Para cada arista de la arborescencia anterior hacer buscar en etiquetas los vértices [u,v] de esa arista Si la búsqueda devuelve [u,-1] hacer buscar aristas entrantes ciclo y guardar mínima [u,x] en nueva arborescencia vértice entrada ciclo = x En otro caso si la búsqueda devuelve [-1,v] hacer buscar aristas salientes ciclo y guardar mínima [y,v] en nueva arborescencia En otro caso // u>-1 y v>-1 obligatoriamente guardar [u,v] en resto aristas Fin si Fin para // Seleccionar aristas interiores del ciclo formar lista aristas ciclo y desechar la incidente en vértice "x" de entrada ciclo agregar estas aristas a nueva arborescencia // Incorporar resto de aristas no relacionadas con las anteriores agregar a nueva arborescencia las del resto aristas arborescencia = nueva arborescencia Fin para Devolver arborescencia
Empecemos viendo la fase de contracción con las variables previas. Obtenemos las aristas edges con getEdges(), pues en los algoritmos de la aplicación siempre nos viene el grafo presentado en una matriz de adyacencia (argumento matrix). Para este algoritmo necesitamos una lista de aristas, donde una arista será como [u,v,w] para designar la arista dirigida "u🡒v" con peso "w".
...
if (temp = getEdges({matrix, edgesCompact:true, weights:true}), typeof temp==="string") throw new Error(temp);
let edges = temp;
let vertexs = Array.from({length:n}, (v,i) => i);
let labels = Array.from({length:n}, (v,i) => [i]);
let edgesItems = [edges];
let vertexsItems = [vertexs];
let labelsItems = [labels];
let edgesTree = [];
let k = 0;
// Contraction phase
while (edgesTree.length===0) {
iter++;
if (iter>maxIter) throw new Error(`The maximum number of iterations ${maxIter} was reached`);
edges = getMinInEdges(edges, vertexs, root);
let edgesZero = getEdgesZero(edges);
let matrixZero = getMatrix(edgesZero, vertexs, root);
if (isDST(matrixZero, root, labels)) {
edgesTree = edgesZero;
} else {
let cycle = getCycle(matrixZero, vertexs);
temp = contract(edges, cycle, root);
[edges, vertexs, labels] = temp;
k++;
edgesItems.push(JSON.parse(JSON.stringify(edges)));
vertexsItems.push(JSON.parse(JSON.stringify(vertexs)));
labelsItems.push(JSON.parse(JSON.stringify(labels)));
}
}
...Como en nuestra aplicación los algoritmos trabajan con la matriz de adyacencia, la lista de vértices de un grafo con n nodos siempre será la lista correlativa de enteros 0, 1, 2, 3, ..., n-1. Sin embargo en este algoritmo no vamos a trabajar con la matriz de adyacencia original sino con una lista de aristas que en cada contracción modifica los "titulos" de los vértices. En medio hacemos una conversión a matriz de adyacencia para comprobar si es una arborescencia u obtener el ciclo, pero en el resto trabajaremos con la lista de aristas. Así como vimos en un ejemplo anterior en un paso podemos tener estas aristas, vértices y etiquetas tras una contracción:
Edges: [[0,1,6],[0,1,8],[0,1,1],[1,5,0],[1,5,4]], Vertexs: [0,1,5], Labels: [[0],[1,4,2,3],[5]]
Se trata de un grafo inicial con 6 nodos, del "0" al "5", donde en un paso hemos contraido los nodos del ciclo [1,4,2,3]. Así que ahora tenemos 3 vértices (Vertexs): el "0", el "1" que es la cabecera del ciclo y el "5". Es necesario mantener esta correspondencía de vértices para poder identificar correctamente las aristas. En las etiquetas (Labels) vemos que las posiciones con más de un vértice son las de un ciclo contraido. Sólo puede haber una de estas posiciones con más de un vértice, pues se contrae un único ciclo en cada paso.
Almacenamos la lista de aristas edgesItems, de vértices vertexsItems y etiquetas labelsItems de cada paso, pues las necesitaremos en pasos posteriores y en la fase de expansión. La variable edgesTree contendrá la lista de aristas de la arborescencia, que iremos modificando tanto en la fase de contracción como en la de expansión, devolviéndose finalmente como arborescencia de mínimo coste del algoritmo.
El bucle while de la fase de contracción itera hasta que encontremos una arborescencia. Lo primero es obtener las aristas mínimas con edges = getMinInEdges(edges, vertexs, root) usando la función auxiliar siguiente:
function getMinInEdges(edges=[], vertexs=[], root=0) {
for (let j of vertexs) {
if (j!==root) {
let indexes = [];
let minEdge = Infinity;
for (let i=0; i<edges.length; i++) {
let [u, v, w] = edges[i];
if (j===v) {
indexes.push(i);
if (w<minEdge) minEdge = w;
}
}
for (let index of indexes) {
edges[index][2] -= minEdge;
}
}
}
return edges;
}La función recibe las aristas edges y devuelve esa misma lista modificando sus pesos. Recuerde que en JavaScript los objetos se pasan por referencia, por lo que no sería necesario la sentencia return edges, pero preferimos ponerla para dejar claro que estamos modificando y devolviendo esa lista. El funcionamiento es iterar por todos los nodos menos el raíz, buscando la menor de las aristas entrantes a cada nodo, guardando su menor peso y restándolo de todas las aristas entrantes en ese nodo. Así la/s arista/s de menor peso quedará/n con un peso 0 y las de mayor peso tendrán la diferencia con ese menor peso. En el ejemplo anterior que estamos citando obtenemos así las aristas mínimas que vemos en la traza Edges min:
k = 0,
Edges previous: [[0,1,10],[0,2,10],[0,3,2],[1,4,2],[1,5,4],[2,3,1],[2,5,8],[3,1,4],[4,2,2]],
Vertexs: [0,1,2,3,4,5],
Labels: [[0],[1],[2],[3],[4],[5]],
Root: 0,
Edges min: [[0,1,6],[0,2,8],[0,3,1],[1,4,0],[1,5,0],[2,3,0],[2,5,4],[3,1,0],[4,2,0]],Observe que Edges previous y Edges min es la lista de aristas almacenada en la misma variable edges y trazada en dos momentos, antes y después de aplicar getMinInEdges().
El siguiente paso es obtener las aristas cero con la función auxiliar getEdgesZero() a partir de la listas de aristas ya con peso mínimo (aristas mínimas) que obtuvimos antes:
function getEdgesZero(edges=[]) {
let edgesZero = [];
let incidents = [];
for (let [i, j, w] of edges.values()) {
if (w===0 && !incidents.includes(j)) {
incidents.push(j);
edgesZero.push([i, j]);
}
}
return edgesZero;
}Filtramos las aristas mínimas con peso 0 y si hay varias de ellas incidentes en el mismo nodo sólo tomamos la primera. Finalmente devolvemos una lista de aristas cero sin pesos. En el ejemplo anterior podemos ver este paso:
k = 0,
Edges previous: [[0,1,10],[0,2,10],[0,3,2],[1,4,2],[1,5,4],[2,3,1],[2,5,8],[3,1,4],[4,2,2]],
Vertexs: [0,1,2,3,4,5],
Labels: [[0],[1],[2],[3],[4],[5]],
Root: 0,
Edges min: [[0,1,6],[0,2,8],[0,3,1],[1,4,0],[1,5,0],[2,3,0],[2,5,4],[3,1,0],[4,2,0]],
Edges zero: [[1,4],[1,5],[2,3],[3,1],[4,2]],En este punto es conveniente observar que la lista de aristas cero no tiene pesos, pues no son necesarios al ser todos los pesos 0. Podríamos obtener su matriz de adyacencia, pues luego vamos a tener que comprobar si esa lista es un arborescencia y, en otro caso, si tiene ciclos, para lo cual podríamos servirnos de algoritmos que ya tenemos implementados sobre la matriz de adyacencia. Sin embargo la lista de aristas mínimas no pueden convertise a matriz de adyacencia, pues al tener algunas aristas con peso 0 no son representables en dicha matriz. Así que no podemos usar un algoritmo para la contracción de nodos que ya teníamos implementado, como veremos después.
Entonces vamos a obtener la matriz de adyacencia a partir de la lista de aristas cero con la función auxiliar getMatrix(), que usa el algoritmo convertToAdjacencyMatrix() que convierte una lista de aristas en una matriz de adyacencia:
function getMatrix(edges=[], vertexs=[]) {
let array = [];
let existed = Array.from({length: vertexs.length}, ()=>false);
for (let [i, j] of edges.values()) {
let ii = vertexs.indexOf(i);
let jj = vertexs.indexOf(j)
existed[ii] = true;
existed[jj] = true;
array.push([ii, jj]);
}
for (let i=0; i<existed.length; i++) {
if (!existed[i]) array.push([i, -1]);
}
if (temp = convertToAdjacencyMatrix({array, mode:"edgeList"}), typeof temp==="string") throw new Error(temp);
return temp;
}En primer lugar recordemos que la matriz de adyacencia para un grafo con n vértices siempre tiene índices correlativos 0,1,2,...,n-1 mientras que nuestra lista de vértices en vertexs puede no contener algunos tras una contracción. Así que hemos de correlacionarlos. En el mismo ejemplo anterior tenemos esto en el segundo paso tras una contracción:
Vertexs: [0,1,5], Labels: [[0],[1,4,2,3],[5]], Edges zero: [[0,1],[1,5]],
No podemos convertir directamente la lista de aristas cero [[0,1],[1,5]] pues los vértices [0,1,5] no son correlativos. Para ello iteramos por esa lista de vértices y le damos un índice correlativo:
Vertexs: [0,1,5],
0 1 2
Edges zero: [[0,1],[1,5]]
[[0,1],[1,2]]Así que lo que vamos a convertir a matriz de adyacencia es la lista de aristas [[0,1],[1,2]]. Puede suceder también que falten índices de nodos, como en la lista de aristas cero [[1,4],[1,5],[2,3],[3,1],[4,2]] que vimos antes, con los vértices [0,1,2,3,4,5], faltando el vértice "0". Agregando una arista [0,-1] a lista de aristas servirá para que el algoritmo convertToAdjacencyMatrix() reconozca que ese es un nodo aislado, sin aristas entrantes ni salientes.
Hay que notar que cambiar los números de los vértices para obtener la matriz de adyacencia no afecta al resto del algoritmo, pues lo que vamos a hacer es preguntarnos si esa matriz de adyacencia es una arborescencia, pero no modificamos la lista de aristas cero. Y en caso que no lo sea, obtener los ciclos, pero que al devolver los nodos del ciclo volveremos a reponer los números que antes tenían, como veremos después.
Veamos en primer lugar si la lista de aristas cero es una arborescencia usando la función auxiliar isDST() (is Directed Spanning Tree) y la matriz cero (matrixZero) que acabamos de obtener, haciendo uso del algoritmo ya implementado isGraphArborescence():
function isDST(matrix=[], root=0, labels=[]) {
root = labels.findIndex(v => v.includes(root));
if (temp = isGraphArborescence({matrix, root, directed:true}), typeof temp==="string") throw new Error(temp);
return temp;
}
Observamos que debemos buscar el índice del nodo raíz con root = labels.findIndex(v => v.includes(root)). Para explicar esto vea la arborescencia de coste mínimo para el grafo de la Figura con el nodo raíz "3". Al inicio tenemos los vértices Vertexs: [0,1,2,3,4,5,6] donde el "3" está en la cuarta posición (índice 3) pues inicialmente son correlativos desde 0. En las etiquetas también aparece en esa posición Labels: [[0],[1],[2],[3],[4],[5],[6]]. Si posteriomente contraemos el ciclo [1,2] tendremos los vértices Vertexs: [0,1,3,4,5,6] y las etiquetas Labels: [[0],[1,2],[3],[4],[5],[6]], donde ahora la raíz "3" aparece en la tercera posición (índice 2). Y esa posición hemos de pasarla al argumento root del algoritmo isGraphArborescence() pues es la que tendrá en la matriz de adyacencia.
Si la lista de aristas cero es una arborescencia habremos finalizado la fase de contracción. En otro caso hay un ciclo en esa lista de aristas. Obtenemos ese ciclo haciendo uso del algoritmo ya implementado getCyclesAll() que busca ciclos en cualquier parte del grafo, con el argumento firstMatch: true para que sólo devuelva el primero encontrado. Le pasamos la misma matriz cero (matrixZero) que usamos antes:
function getCycle(matrix=[], vertexs=[]){
if (temp = getCyclesAll({matrix, firstMatch:true, directed:true}), typeof temp==="string") throw new Error(temp);
if (temp.length===0) throw new Error("Error no cycle");
let cycle = temp[0].slice(0, temp[0].length-1);
return cycle.map(v => vertexs[v]);
}El algoritmo getCyclesAll() devuelve un ciclo como [1,4,2,3,1], con el mismo primer y último vértice, siendo el primero siempre el de menor índice. Eliminamos la repeticicón del último y reponemos los números de los vértices haciendo uso de vertexs, tal como explicamos antes cuando convertimos la lista de aristas cero a una matriz de adyacencia.
El último paso en esta fase es la contracción del ciclo. Aquí no podemos usar el algoritmo ya implementado con la operación operateContractionGraph() que, como todos los algoritmos de la aplicación, funciona con una matriz de adyacencia. La lista de aristas (edges), que en este punto son mínimas, tiene algunas aristas con pesos 0. Y no podemos convertir esa lista a matriz de adyacencia para aplicar esa operación operateContractionGraph() ya implementada. Esto es porque una arista "u🡒v" con peso 0 aparece en la matriz de adyacencia con la posición matrix[u][v] = 0, que es como si no existiera, pues solo se convierten en aristas las posiciones que cumplan matrix[u][v] > 0.
Además como vimos en un ejemplo anterior en la Figura, en un momento dado podemos tener unas aristas (que en ese momento son mínimas anteriores) que forman un multigrafo con más de una arista en el mismo sentido entre dos nodos, algo que no puede representarse en una matriz de adyacencia. Esto no pasa con las aristas cero, pues al seleccionarlas solo permitimos una única arista entrante a cada nodo. Así que hemos de fabricarnos una nueva función para contraer un ciclo en el grafo representado por la lista de aristas mínimas anteriores, algunas con peso 0 y con más de una arista en el mismo sentido entre dos nodos.
function contract(edges=[], cycle=[], root=0) {
let minVertexCycle = cycle[0];
let newEdges = [];
for (let edge of edges) {
let [u, v, w] = edge;
if (cycle.includes(v) && !cycle.includes(u)) {
newEdges.push([u, minVertexCycle, w]);
} else if (cycle.includes(u) && !cycle.includes(v)) {
newEdges.push([minVertexCycle, v, w]);
} else if (!cycle.includes(u) && !cycle.includes(v)) {
newEdges.push([u, v, w]);
}
}
let newVertexs = [...new Set(newEdges.map(v => [v[0], v[1]]).flat())].toSorted((u,v) => u-v);
let newLabels = [];
for (let i=0; i<newVertexs.length; i++) {
if (newVertexs[i]===minVertexCycle) {
newLabels.push([...cycle]);
} else if (i===newVertexs[i]) {
newLabels.push([i]);
} else {
newLabels.push([newVertexs[i]]);
}
}
let k = newLabels.findIndex(v => v.includes(root));
if (k===-1 || newLabels[k].length>1) throw new Error(`Wrong root in contract()`);
return [newEdges, newVertexs, newLabels];
}En la primera parte iteramos por todas las aristas mínimas y vamos a traspasarlas a la nueva lista newEdges. Traspasamos las que entran y salen del ciclo, cambiando el vértice de entrada o salida por minVertexCycle, recordando que siempre en un ciclo el primer vértice es el de menor índice, como explicamos más arriba. También traspasamos las aristas externas al ciclo. Al finalizar este primer bucle habremos omitido las aristas del ciclo y sus vértices se sustituyen por el nuevo vértice minVertexCycle. La segunda parte es reetiquetar los vértices en newVertexs y las etiquetas en newLabels, variables que devolvemos y pasarán a ser las nuevas edges, vertexs y labels para el siguiente paso de la fase de contracción.
Al final de la función anterior hacemos una comprobación buscando la raiz en las nuevas etiquetas. La raíz nunca puede formar parte de un ciclo a contraer, puesto que cuando seleccionamos las aristas entrantes en cada nodo omitimos las entrantes al raíz. Así que en la nuevas etiquetas tras la contracción newLabels hacemos la comprobación de que la raíz anterior sigue estando en una etiqueta con solo ese vértice. En el ejemplo de la Figura vimos que la raíz "3" podría cambiar de posición en la lista de vértices que inicialmente era Vertexs: [0,1,2,3,4,5,6] con etiquetas Labels: [[0],[1],[2],[3],[4],[5],[6]] y que tras la contracción de [1,2] quedaba como Vertexs: [0,1,3,4,5,6], pero el número "3" de la raíz permanece invariable en una entrada [3] de las etiquetas tras la contracción Labels: [[0],[1,2],[3],[4],[5],[6]], aunque puede cambiar de posición como es el caso.
Cuando en la fase de contracción encontremos una arborescencia saldremos del bucle while e iniciaremos la fase de expansión.
...
// Expansion phase
for (let k=edgesItems.length-1; k>0; k--){
let edges = edgesItems[k-1];
let labels = labelsItems[k];
let cycle = labels.filter(v => v.length>1)[0];
let newEdgesTree = [];
let vertexInCycle = null;
let restEdges = [];
for (let [i,j] of edgesTree.values()) {
let u = labels.findIndex(x => x.length===1 && x[0]===i);
let v = labels.findIndex(x => x.length===1 && x[0]===j);
if (u>-1 && v===-1) {
u = labels[u][0];
let minEdge = edges.filter(x => x[0]===u && cycle.includes(x[1]));
minEdge = minEdge.toSorted((x,y) => x[2]-y[2])[0];
vertexInCycle = minEdge[1];
newEdgesTree.push([minEdge[0], minEdge[1]]);
} else if (u===-1 && v>-1) {
v = labels[v][0];
let minEdge = edges.filter(x => cycle.includes(x[0]) && x[1]===v);
minEdge = minEdge.toSorted((x,y) => x[2]-y[2])[0];
newEdgesTree.push([minEdge[0], minEdge[1]]);
} else {
restEdges.push([i, j]);
}
}
cycle.push(cycle[0]);
for (let i=1; i<cycle.length; i++) {
let [u, v] = [cycle[i-1], cycle[i]];
if (v!==vertexInCycle) {
newEdgesTree.push([u, v])
}
}
newEdgesTree.push(...restEdges);
edgesTree = newEdgesTree;
}
...Finalizamos la fase de contracción con la arborescencia obtenida en la variable edgesTree, como [[0,1],[1,5]], según vimos en un ejemplo anterior. Se trata de un bucle for que itera desde el último paso hasta k=1. En cada paso k recuperamos las aristas que teníamos almacenadas en el paso anterior edges = edgesItems[k-1] y las etiquetas labels = labelsItems[k] de ese paso. Si las etiquetas son como vimos en ese ejemplo anterior [[0],[1,4,2,3],[5]], donde [1,4,2,3] es un ciclo, entonces iteramos por edgesTree para seleccionar las aristas entrantes y salientes al ciclo . Así la primera arista de edgesTree es [0,1] encontrando [0] en las etiquetas pero no [1], es que "1" está en el ciclo, así que todas las aristas de la forma "0🡒1", "0🡒4", "0🡒2", "0🡒3" serán entrantes al ciclo, así que las buscamos en las aristas edges y seleccionamos la menor de ella que pasará a forma parte de la nueva arborescencia que estamos formando. Y de la misma forma hacemos para las ariastas salientes al ciclo. Si una arista de edgesTree no es entrante ni saliente al ciclo la guardamos en restEdges para incoporarlas también a la arborescencia final.
El siguiente paso es seleccionar las aristas interiores del ciclo, que con el ciclo [1,4,2,3] son "1🡒4", "4🡒2", "2🡒3", "3🡒1". Antes cuando seleccionamos la arista entrante al ciclo "u🡒v" ese "v" lo guardamos como vertexInCycle, así que de esas aristas interiores del ciclo desechamos la que tenga ese "v", guardando el resto en la arborescencia final.
Salimos de la fase de expansión devolviendo la arborescencia final en edgesTree, tras lo cual las pasamos a result.edges que devolverá el algoritmo, ordenándolas por los vértices, aunque no necesario nos permitirá una mejor visualización. También obtenemos el peso total en result.weight directamente desde la matriz inicial que se recibió en el algoritmo:
result.edges = edgesTree.toSorted((u,v) => u[0]===v[0] ? u[1]-v[1] : u[0]-v[0]); result.weight = edgesTree.reduce((p,v) => (p+=matrix[v[0]][v[1]], p), 0);
Arborescencia de mínimo coste en Wolfram
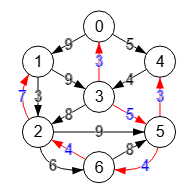
En la Figura vemos un grafo que ya hemos usado antes, aplicando ahora el algoritmo getMinimumCostArborescenceNoRoot() para obtener la arborescencia de mínimo coste sin especificar raíz, algoritmo voraz que no siempre consigue la solución óptima. Obtiene [[1,2],[3,0],[5,4],[4,3],[5,6],[0,1]] desde la raíz "5" con peso 26.
Arborescencia de mínimo coste sin raíz: {
"edges":[[1,2],[3,0],[5,4],[4,3],[5,6],[0,1]],
"weight":26,
"root":5,
"warnings":[],
"newEdges":[],
"trace":[]}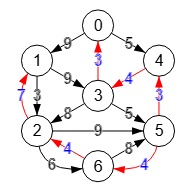
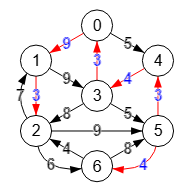
Si marcamos la opcion encontrar raíz mínima para este algoritmo (ver Figura), nos devolverá la arborescencia [[2,1],[3,0],[4,3],[5,4],[5,6],[6,2]] como vemos en la Figura, también con raíz "5" pero con menor peso total 25. Observe que en lugar de las aristas "0🡒1" y "1🡒2" con pesos 9+3=12 devuelve "6🡒2" y "2🡒1" con pesos 4+7=11 menor.
Arborescencia de mínimo coste sin raíz: {
"edges":[[2,1],[3,0],[4,3],[5,4],[5,6],[6,2]],
"weight":25,
"root":5,
"warnings":[],
"newEdges":[],
"trace":[]}
{"nodes":[
{"index":0,"nodeOffset":"19.17 11.78","parent":[{"index":-1},{"index":1,"value":9},{"index":4,"value":5}]},
{"index":1,"nodeOffset":"-5.27 0.89","parent":[{"index":3,"value":9},{"index":2,"value":3}]},
{"index":2,"nodeOffset":"3.06 4.11","parent":[{"index":5,"value":9},{"index":6,"lineType":"quadratic","lineOffset":"-2 2","value":6},{"index":1,"lineType":"quadratic","lineOffset":-2,"value":7}]},
{"index":3,"nodeOffset":"2.5 -10","parent":[{"index":2,"value":8},{"index":0,"value":3},{"index":5,"value":5}]},
{"index":4,"nodeOffset":"1.94 -24.11","parent":[{"index":3,"value":4}]},
{"index":5,"nodeOffset":"10.27 29.11","parent":[{"index":4,"value":3},{"index":6,"lineType":"quadratic","lineOffset":"2 2","value":4}]},
{"index":6,"nodeOffset":"-14.17 68.22","parent":[{"index":2,"value":4},{"index":5,"value":8}]}
],
"config":{
"markerEnd":"arrow",
"algorithm":"Minimum cost arborescence no root",
"findMinRoot":true
}}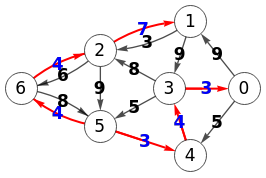
La aplicación exporta a Wolfram usando la función FindSpanningTree para lo que pasamos FindSpanningTree[g, Method -> "MinimumCostArborescence"], con el método para ejecutar una arborescencia de coste mínimo. Otros métodos pueden ser "Prim" y "Kruskal" que ya explicamos en el tema anterior para los árboles de recubrimiento mínimo. Observe que no especificamos ninguna raíz en esa función, con lo que Wolfram buscará la raíz para conseguir una arborescencia mínima.
En la Figura vemos que obtiene la misma arborescencia con peso 25 también con la raíz en el nodo "5". Si en el código quitamos el punto y coma final de la línea e = EdgeList[%] veremos la lista de aristas {3🡒2, 4🡒1, 5🡒4, 6🡒5, 6🡒7, 7🡒3}, que recordando que Wolfram inicia siempre las listas con índice "1", restando uno de cada posición resulta la misma que encontramos en nuestra aplicación: {2🡒1, 3🡒0, 4🡒3, 5🡒4, 5🡒6, 6🡒2}.
g = WeightedAdjacencyGraph[{{∞,9,∞,∞,5,∞,∞},{∞,∞,3,9,∞,∞,∞},{∞,7,∞,∞,∞,9,6},{3,∞,8,∞,∞,5,∞},{∞,∞,∞,4,∞,∞,∞},{∞,∞,∞,∞,3,∞,4},{∞,∞,4,∞,∞,8,∞}},
ImageSize -> 266, VertexSize -> {"Scaled", 0.12}, VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center], 3 -> Placed[2,Center], 4 -> Placed[3,Center],
5 -> Placed[4,Center], 6 -> Placed[5,Center], 7 -> Placed[6,Center]}, VertexLabelStyle -> Directive[Black,17.5], EdgeLabelStyle -> Directive[Black,17.5,Bold],
EdgeLabels -> {(1->2)->9, (1->5)->5, (2->4)->9, (2->3)->3, (3->6)->9, (3->7)->6, (3->2)->7, (4->3)->8, (4->1)->3,
(4->6)->5, (5->4)->4, (6->5)->3, (6->7)->4, (7->3)->4,
(7->6)->8}, VertexStyle -> White, DirectedEdges -> True, EdgeStyle -> {{Black,Thickness[0.005]}}];
FindSpanningTree[g, Method->"MinimumCostArborescence"];
e = EdgeList[%];
HighlightGraph[g,{Style[e, Red, Thick], Annotation[e, EdgeLabelStyle-Directive[Blue,17.5,Bold]]}]
Total[PropertyValue[{g, e}, EdgeWeight]]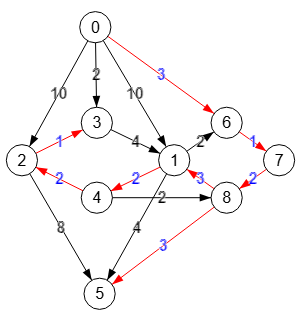
En la Figura vemos otro grafo donde aplicamos getMinimumCostArborescenceEdmonds() que implementa el algoritmo de Edmonds para encontrar una arborescencia de coste mínimo, especificando en este caso desde la raíz "0". Obtenemos la lista de aristas [[0,6],[1,4],[2,3],[4,2],[6,7],[7,8],[8,1],[8,5]] con suma de pesos 17.
Arborescencia de mínimo coste Edmonds: {
"edges":[[0,6],[1,4],[2,3],[4,2],[6,7],[7,8],[8,1],[8,5]],
"weight":17,
"warnings":[],
"trace":[]}
{"nodes":[
{"index":0,"nodeOffset":"18.07 -0.8","parent":[{"index":1,"value":10},{"index":2,"value":10},{"index":3,"value":2},{"index":6,"value":3}]},
{"index":1,"nodeOffset":"66.33 2.5","parent":[{"index":4,"value":2},{"index":5,"value":4},{"index":6,"value":2}]},
{"index":2,"nodeOffset":"-11.33 2.5","parent":[{"index":3,"value":1},{"index":5,"value":8}]},
{"index":3,"nodeOffset":"2 -12.5","parent":[{"index":1,"value":4}]},
{"index":4,"nodeOffset":"-14.67 17.5","parent":[{"index":2,"value":2},{"index":8,"value":2}]},
{"index":5,"nodeOffset":"-13.56 106","parent":[{"index":-1}]},
{"index":6,"nodeOffset":"20.67 -12.5","parent":[{"index":7,"value":1}]},
{"index":7,"nodeOffset":"75 -22.5","parent":[{"index":8,"value":2}]},
{"index":8,"nodeOffset":"54 42.5","parent":[{"index":1,"value":3},{"index":5,"value":3}]}
],
"config":{
"markerEnd":"arrow",
"algorithm":"Minimum cost arborescence Edmonds"
}}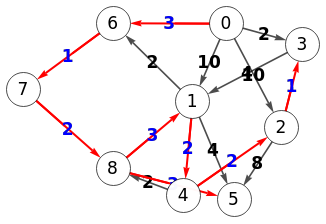
Con FindSpanningTree en Wolfram aplicando FindSpanningTree[{g, 1}, Method -> "MinimumCostArborescence"] donde ahora especificamos la raíz "1" con {g, 1}, que se corresponde con la raíz "0" en nuestra aplicación pues Wolfram inicia índices en 1, vemos que se obtiene el mismo resultado con peso total 17. Obtiene en e = EdgeList[%] la lista de aristas {1🡒7, 2🡒5, 3🡒4, 5🡒3, 7🡒8, 8🡒9, 9🡒2, 9🡒6}, que tras ajustar índices es la misma que la nuestra: {0🡒6, 1🡒4, 2🡒3, 4🡒2, 6🡒7, 7🡒8, 8🡒1, 8🡒5}.
g = WeightedAdjacencyGraph[{{∞,10,10,2,∞,∞,3,∞,∞},{∞,∞,∞,∞,2,4,2,∞,∞},{∞,∞,∞,1,∞,8,∞,∞,∞},{∞,4,∞,∞,∞,∞,∞,∞,∞},{∞,∞,2,∞,∞,∞,∞,∞,2},
{∞,∞,∞,∞,∞,∞,∞,∞,∞},{∞,∞,∞,∞,∞,∞,∞,1,∞},{∞,∞,∞,∞,∞,∞,∞,∞,2},{∞,3,∞,∞,∞,3,∞,∞,∞}}, ImageSize -> 326,
VertexSize -> {"Scaled", 0.1}, VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center], 3 -> Placed[2,Center], 4 -> Placed[3,Center],
5 -> Placed[4,Center], 6 -> Placed[5,Center], 7 -> Placed[6,Center], 8 -> Placed[7,Center], 9 -> Placed[8,Center]},
VertexLabelStyle -> Directive[Black,17.5], EdgeLabelStyle -> Directive[Black,17.5,Bold], EdgeLabels -> {(1->2)->10, (1->3)->10, (1->4)->2, (1->7)->3,
(2->5)->2, (2->6)->4, (2->7)->2, (3->4)->1, (3->6)->8, (4->2)->4, (5->3)->2, (5->9)->2, (7->8)->1, (8->9)->2,
(9->2)->3, (9->6)->3}, VertexStyle -> White,
DirectedEdges -> True, EdgeStyle -> {{Black,Thickness[0.005]}}];
FindSpanningTree[{g, 1}, Method->"MinimumCostArborescence"];
e = EdgeList[%];
HighlightGraph[g,{Style[e, Red, Thick], Annotation[e, EdgeLabelStyle->Directive[Blue,17.5,Bold]]}]
Total[PropertyValue[{g, e}, EdgeWeight]]