10 dic 2025

Caminos mínimos en grafos

Algoritmo de Dijkstra para buscar los caminos mínimos en un grafo `getShortestPathDijkstra()`

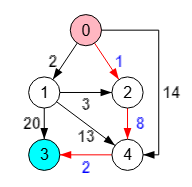
*Figura*. Camino mínimo Dijkstra entre nodos "0" y "3"

Encontrar los caminos mínimos en un grafo dirigido supone definir un nodo raíz y buscar los caminos al resto de nodos con suma de longitudes mínima. En la Figura vemos el camino mínimo entre los nodos "0" y "3" con suma de longitudes 11 obtenido con el algoritmo de Dijkstra de caminos mínimos, donde se resaltan el primer y último nodo así como las aristas del camino con diferentes colores. Las longitudes son los valores de las aristas, que según el problema puede denominarse pesos, capacidades o cualquier otra cosa. En principio se define para grafos dirigidos, pero luego veremos que también puede aplicarse a no dirigidos. Es imprescindible que las longitudes de las aristas no sean negativas. Para este caso se usa el algoritmo de Bellman-Ford que aún no he implementado.

Ya traté este problema en el año 2020 en el tema algoritmo de Dijkstra de caminos mínimos con ocasión de exponer un ejemplo de aplicación de algoritmos voraces. Ahora lo incorporo en la aplicación Grafos SVG con algunas mejoras en la presentación y trazado.

La aplicación devuelve el siguiente resultado con el camino que recorre los nodos "paths":[[0,2,4,3]] con suma de longitudes 11. Observamos en "pathLengths": [0, 2, 1, 11, 9] las longitudes de los caminos desde cada nodo, así desde el nodo "0" hasta "0" la longitud es cero, mientras que al resto de nodos 1, 2, 3, 4 vemos las longitudes mínimas 2, 1, 11, 9 con lo que la longitud mínima al nodo "3" es 11.

Camino mínimo (Dijkstra) desde el nodo 0 hasta 3: {
"paths":[[0,2,4,3]],
"pathLengths":[0,2,1,11,9],
"pointers":[0,0,0,4,2],
"trace":[]}

Con este JSON puede importar el ejemplo.

{"nodes":[
    {"index":0,"parent":[{"index":-1}]},
    {"index":1,"parent":[{"index":0,"value":2,"lineTextOffset":-0.8}]},
    {"index":2,"parent":[{"index":0,"value":1,"lineTextOffset":0.8},{"index":1,"value":3,"lineTextOffset":"0 0.8"}]},
    {"index":3,"parent":[{"index":1,"value":20,"lineTextOffset":-0.8},{"index":4,"value":2,"lineTextOffset":"0 0.8"}]},
    {"index":4,"parent":[{"index":1,"value":13,"lineTextOffset":"0 0.8"},{"index":2,"value":8,"lineTextOffset":0.8},{"index":0,"value":14,"lineOffset":"1","lineTextOffset":0.8}]}
],
"config":{
    "markerStart":"arrow",
    "algorithm":"Shortest path (Dijkstra)",
    "lastIndex":3
}}

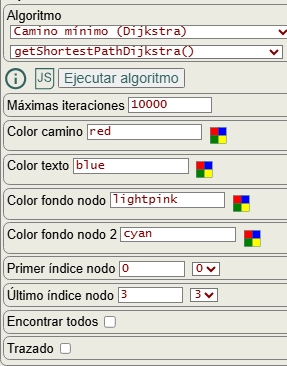
En la Figura vemos las opciones para ejecutar el algoritmo, con primer índice de nodo o nodo raíz y último índice de nodo. Si activamos encontrar todos se ignora el último índice de nodo y buscará todos los caminos mínimos entre la raíz y el resto de nodos, mostrándose en la aplicación por medio de los botones de navegación que encontrará en la parte superior derecha del SVG.

Con la opción trazado se devuelve una traza de la ejecución. Las otras opciones color camino, color texto, color fondo nodo y color fondo nodo 2 no se pasan al algoritmo y sólo sirven para, tras su ejecución, resaltar en el SVG mostrado en pantalla el color de las aristas del camino, color texto de las aristas y colores de los nodos de inicio y final del camino.

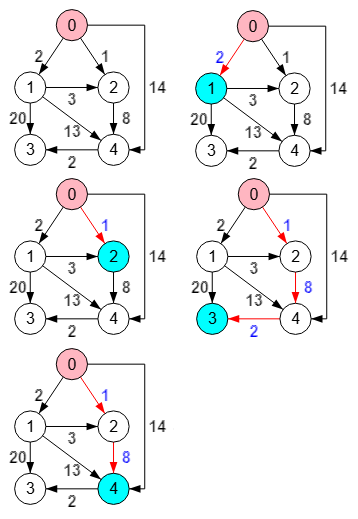
En la Figura vemos los caminos mínimos entre el nodo "0" y el resto de nodos del mismo ejemplo anterior. Observe que del nodo "0" al "0" la distancia es cero, con lo que no hay camino o mejor dicho, el camino es vacío. Los caminos devueltos son "paths":[[],[0,1],[0,2],[0,2,4,3],[0,2,4]] como se observa en la traza del siguiente resultado obtenido.

La ejecución es la misma independiente de si activamos encontrar todos, pues el algoritmo en cualquier caso encontrará las distancias mínimas "pathLengths": [0, 2, 1, 11 ,9] entre el nodo raíz y el resto de nodos. El resultado "pointers": [0, 0, 0, 4, 2] son unos punteros que permiten reconstruir los caminos entre la raíz "0" y el resto de nodos, como veremos después.

Ya explicamos el funcionamiento de este algoritmo en el tema con el algoritmo de Dijkstra pero vamos a exponer otra vez esa explicación sobre la siguiente traza.

Time: 0 ms

Camino mínimo (Dijkstra) desde el nodo 0 hasta todos: {
"paths":[[],[0,1],[0,2],[0,2,4,3],[0,2,4]],
"pathLengths":[0,2,1,11,9],
"pointers":[0,0,0,4,2],
"trace":"
INICIO:
edgeLengths = [
  [0,2,1,∞,14]
  [∞,0,3,20,13]
  [∞,∞,0,∞,8]
  [∞,∞,∞,0,∞]
  [∞,∞,∞,2,0]
]
pathLengths = [0,2,1,∞,14]
candidates = [1,2,3,4]
pointers = [0,0,0,0,0]

BUCLE VORAZ:
(1) k=2 
pathLengths = [0,2,1,∞,9]
candidates = [1,3,4]
pointers = [0,0,0,0,2]

(2) k=1 
pathLengths = [0,2,1,22,9]
candidates = [3,4]
pointers = [0,0,0,1,2]

(3) k=4 
pathLengths = [0,2,1,11,9]
candidates = [3]
pointers = [0,0,0,4,2]

(4) k=3 
pathLengths = [0,2,1,11,9]
candidates = []
pointers = [0,0,0,4,2]


CONSTRUIR CAMINOS:
From 0 to 0
    path = []
From 0 to 1
    path = [1]
    pointers[1] = 0
    path = [0,1]
From 0 to 2
    path = [2]
    pointers[2] = 0
    path = [0,2]
From 0 to 3
    path = [3]
    pointers[3] = 4
    path = [4,3]
    pointers[4] = 2
    path = [2,4,3]
    pointers[2] = 0
    path = [0,2,4,3]
From 0 to 4
    path = [4]
    pointers[4] = 2
    path = [2,4]
    pointers[2] = 0
    path = [0,2,4]"}

Con este JSON se puede importar el ejemplo:

{"nodes":[
    {"index":0,"parent":[{"index":-1}]},
    {"index":1,"parent":[{"index":0,"value":2,"lineTextOffset":-0.8}]},
    {"index":2,"parent":[{"index":0,"value":1,"lineTextOffset":0.8},{"index":1,"value":3,"lineTextOffset":"0 0.8"}]},
    {"index":3,"parent":[{"index":1,"value":20,"lineTextOffset":-0.8},{"index":4,"value":2,"lineTextOffset":"0 0.8"}]},
    {"index":4,"parent":[{"index":1,"value":13,"lineTextOffset":"0 0.8"},{"index":2,"value":8,"lineTextOffset":0.8},{"index":0,"value":14,"lineOffset":"1","lineTextOffset":0.8}]}
],
"config":{
    "markerStart":"arrow",
    "algorithm":"Shortest path (Dijkstra)",
    "lastIndex":3,
    "findAll":true,
    "tracing":true
}}

El primer paso es el INICIO donde preparamos las variables que intervendrán en el siguiente bucle voraz. En el algoritmo recibimos una matriz de adyacencia en modo valores "0/number" o "0/1", con lo que cada posición de la matriz es un número mayor o igual que cero. Obtenemos la matriz longitudes de aristas edgeLengths a partir de la matriz de adyacencia simplemente cambiando 0 por el número Infinity de JavaScript menos en la diagonal que aseguramos que haya un cero, eliminando así los autobucles si existieran. En la traza representamos infinito con el caracter "∞" sin olvidar que en el código JavaScript este valor es Infinity.

Iniciamos la variable longitudes de caminos pathLengths simplemente recuperando la primera fila de la matriz edgeLengths obteniendo pathLengths = [0,2,1,∞,14] que vienen a ser las distancias de las aristas directas desde el nodo raíz "0" al resto de nodos. La variable candidatos son el resto de nodos menos la raíz "0" obteniendo candidates = [1,2,3,4]. En los punteros pointers = [0,0,0,0,0] tenemos un Array con tantos ceros como nodos del grafo.

INICIO:
edgeLengths = [
  [0,2,1,∞,14]
  [∞,0,3,20,13]
  [∞,∞,0,∞,8]
  [∞,∞,∞,0,∞]
  [∞,∞,∞,2,0]
]
pathLengths = [0,2,1,∞,14]
candidates = [1,2,3,4]
pointers = [0,0,0,0,0]

A continuación ejecutamos el bucle voraz donde en cada iteración seleccionamos un nodo de los candidatos candidates = [1,2,3,4], aunque como veremos después, sólo es necesario iterar por los tres primeros. Veamos los pasos de la traza incluyendo en cada paso la situación de variables al finalizar el paso. Con este párrafo se incluyen las variables al inicio.

(1) k=2 
pathLengths = [0,2,1,∞,9]
candidates = [1,3,4]
pointers = [0,0,0,0,2]

En la iteración 1 seleccionamos el candidato que esté más cerca del nodo raíz "0", observando en las longitudes de caminos pathLengths = [0,2,1,∞,14] que es el nodo k=2 que está a una longitud pathLengths[2] = 1 del nodo raíz. Eliminamos ese k=2 de la lista de candidatos quedando candidates = [1,3,4]. Actualizamos las longitudes de caminos anterior pathLengths = [0,2,1,∞,14] y punteros anterior pointers = [0,0,0,0,0] para los índices j ∈ [1,3,4] de los candidatos faltantes (resaltados en amarillo). Para ello observamos la fila k=2 de la matriz longitudes aristas edgeLengths[2] = [∞,∞,0,∞,8] observando si pathLenghts[j] > pathLenghts[2] + edgesLength[2][j] siendo para los tres casos pathLengths[2] = 1:

j = 1 ⇒ pathLengts[1] = 2, edgesLength[2][1] = ∞ ⇒ 2 ≯ 1+∞ = ∞ donde el símbolo "≯ " signifca "no mayor que".
j = 3 ⇒ pathLengts[3] = ∞, edgesLength[2][3] = ∞ ⇒ ∞ ≯ 1+∞ = ∞
j = 4 ⇒ pathLengts[4] = 14, edgesLength[2][4] = 8 ⇒ 14 > 1+8 = 9, actualizamos pointers[j] = k quedando pointers[4] = 2. Entonces actualizamos pathLengths = [0,2,1,∞,9] y pointers = [0,0,0,0,2].

(2) k=1 
pathLengths = [0,2,1,22,9]
candidates = [3,4]
pointers = [0,0,0,1,2]

En la iteración 2 el nodo más cercano a la raíz "0" de los candidatos es k=1 pues pathLengths[1] = 2 quedando candidates = [3,4]. Observamos en pathLengths = [0,2,1,∞,9] y en edgesLengths[1] = [∞,0,3,20,13] comprobando pathLenghts[j] > pathLenghts[1] + edgesLength[1][j] lo que sucede para j=3 pues ∞ > 2+20 = 22 pero no para j=4 pues 9 < 2+13. Actualizamos pathLengths = [0,2,1,22,9] y pointers = [0,0,0,1,2].

(3) k=4 
pathLengths = [0,2,1,11,9]
candidates = [3]
pointers = [0,0,0,4,2]

En la iteración 3 el nodo más cercano a la raíz "0" de los candidatos es k=4 pues pathLengths[4] = 9 quedando candidates = [3]. Observamos en pathLengths = [0,2,1,22,9] y en edgesLengths[4] = [∞,∞,∞,2,0] comprobando pathLenghts[j] > pathLenghts[4] + edgesLength[4][j] lo que sucede para el único candidato j=3 pues 22 > 9+2 = 11. Actualizamos pathLengths = [0,2,1,11,9] y pointers = [0,0,0,4,2].

(4) k=3 
pathLengths = [0,2,1,11,9]
candidates = []
pointers = [0,0,0,4,2]

En la iteración 4 el nodo más cercano a la raíz "0" de los candidatos es el único que queda k=3 quedando candidates = []. Esto quiere decir que no vamos a modificar pathLengths ni pointers, por lo que este último paso puede omitirse en el algoritmo quedando esas variables como estaban en el paso anterior. Si los candidatos antes de iniciar el bucle voraz eran [1,2,3,4] en el algoritmo siempre podemos iterar por los tres primeros que se seleccionen finalizando cuando quede un candidato.

From 0 to 3
    path = [3]
    pointers[3] = 4
    path = [4,3]
    pointers[4] = 2
    path = [2,4,3]
    pointers[2] = 0
    path = [0,2,4,3]

Tras el bucle voraz tenemos otro para construir los caminos que se soliciten en el algoritmo. Para obtener un camino entre el nodo raíz y otro nodo usaremos la variable punteros pointers = [0,0,0,4,2] y longitudes de caminos pathLengths = [0,2,1,11,9]. Supongamos que hemos de recuperar el camino de "0" a "3" que recorre los nodos [0,2,4,3]. En un array declaramos el camino path = [3] con el último índice del camino a buscar. Si pathLengths[3] = 11 es finito sabemos que hay un camino desde el nodo "0" cuyo suma de longitudes es 11. Si fuera infinito no habría camino. Entonces iremos desreferenciando con un bucle hasta que lleguemos al nodo raíz "0" tal como vemos en el esquema adjunto.

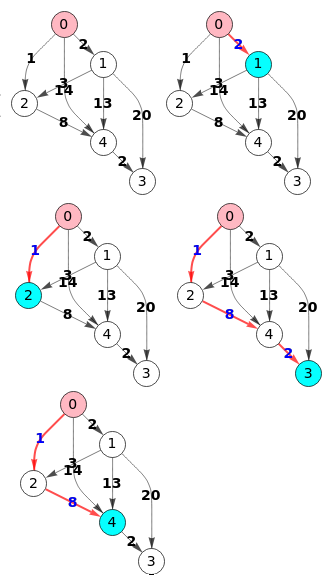
En Wolfram se usa la función FindShortestPath[g, s, t, m] para encontrar el camino mínimo entre "s" y "t" usando el método "m". Los argumentos "s" y "t" pueden ser los números desde 1 para los nodos o "All". En nuestra aplicación para este algoritmo Dijkstra sólo es posible que "t" pueda ser "All", aunque luego veremos el algoritmo de Floyd donde se buscan todos los caminos desde todos los nodos, presentándose en Wolfram usando ambos "All".

Los métodos "m" en Wolfram pueden ser "Dijkstra" o "BellmanFord", siendo este algoritmo de Bellman-Ford uno que no he implementado y que encuentra el camino mínimo con aristas con pesos negativos.

En la Figura vemos FindShortestPath[g, 1, All, Method -> "Dijkstra"] que encuentra los caminos mínimos desde el nodo "1" ("0" en nuestra aplicación) al resto de nodos, resultado igual que el que obtuvimos.

g = WeightedAdjacencyGraph[{{∞,2,1,∞,14},{∞,∞,3,20,13},{∞,∞,∞,∞,8},{∞,∞,∞,∞,∞},{∞,∞,∞,2,∞}}, ImageSize -> 150, VertexSize -> {"Scaled", 0.13}, 
VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center], 3 -> Placed[2,Center], 4 -> Placed[3,Center], 5 -> Placed[4,Center]}, VertexLabelStyle -> Directive[Black,14], 
EdgeLabelStyle -> Directive[Black,14,Bold], EdgeLabels -> {(1->2)->2, (1->3)->1, (2->3)->3, (2->4)->20, (5->4)->2, (2->5)->13, (3->5)->8, (1->5)->14}, 
VertexStyle -> White, DirectedEdges -> True, EdgeStyle -> {{Black,Thickness[0.005]}}];
f = FindShortestPath[g, 1, All, Method -> "Dijkstra"];
t = Table[PathGraph[f[i], DirectedEdges->True], {i, VertexList[g]}];
Table[HighlightGraph[g,{Style[First[VertexList[p]], RGBColor["lightpink"]], Style[Last[VertexList[p]], If[First[VertexList[p]]!=Last[VertexList[p]], Cyan]],Style[EdgeList[p], Red, Thick], Annotation[EdgeList[p], EdgeLabelStyle->Directive[Blue,14,Bold]]}], {p, t}]

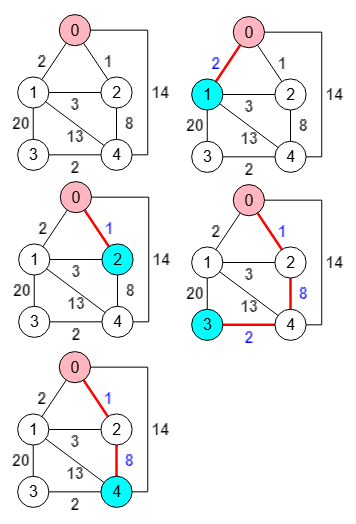
En principio encontrar los caminos mínimos con el algoritmo de Dijkstra se aplica a un grafo dirigido, pero también funcionará sobre un grafo no dirigido. En la Figura vemos todos los caminos mínimos para la versión no dirigida del mismo grafo que vimos en la Figura.

Time: 0 ms

Camino mínimo (Dijkstra) desde el nodo 0 hasta todos: {
"paths":[[],[0,1],[0,2],[0,2,4,3],[0,2,4]],
"pathLengths":[0,2,1,11,9],
"pointers":[0,0,0,4,2],
"trace":"
INICIO:
edgeLengths = [
  [0,2,1,∞,14]
  [2,0,3,20,13]
  [1,3,0,∞,8]
  [∞,20,∞,0,2]
  [14,13,8,2,0]
]
pathLengths = [0,2,1,∞,14]
candidates = [1,2,3,4]
pointers = [0,0,0,0,0]

BUCLE VORAZ:
(1) k=2 
pathLengths = [0,2,1,∞,9]
candidates = [1,3,4]
pointers = [0,0,0,0,2]

(2) k=1 
pathLengths = [0,2,1,22,9]
candidates = [3,4]
pointers = [0,0,0,1,2]

(3) k=4 
pathLengths = [0,2,1,11,9]
candidates = [3]
pointers = [0,0,0,4,2]

(4) k=3 
pathLengths = [0,2,1,11,9]
candidates = []
pointers = [0,0,0,4,2]


CONSTRUIR CAMINOS:
From 0 to 0
    path = []
From 0 to 1
    path = [1]
    pointers[1] = 0
    path = [0,1]
From 0 to 2
    path = [2]
    pointers[2] = 0
    path = [0,2]
From 0 to 3
    path = [3]
    pointers[3] = 4
    path = [4,3]
    pointers[4] = 2
    path = [2,4,3]
    pointers[2] = 0
    path = [0,2,4,3]
From 0 to 4
    path = [4]
    pointers[4] = 2
    path = [2,4]
    pointers[2] = 0
    path = [0,2,4]"}

Con este JSON puede importar el ejemplo.

{"nodes":[
    {"index":0,"parent":[{"index":-1}]},
    {"index":1,"parent":[{"index":0,"value":2,"lineTextOffset":-0.8}]},
    {"index":2,"parent":[{"index":0,"value":1,"lineTextOffset":0.8},{"index":1,"value":3,"lineTextOffset":"0 0.8"}]},
    {"index":3,"parent":[{"index":1,"value":20,"lineTextOffset":-0.8},{"index":4,"value":2,"lineTextOffset":"0 0.8"}]},
    {"index":4,"parent":[{"index":1,"value":13,"lineTextOffset":"0 0.8"},{"index":2,"value":8,"lineTextOffset":0.8},{"index":0,"value":14,"lineOffset":"1","lineTextOffset":0.8}]}
],
"config":{
    "algorithm":"Shortest path (Dijkstra)",
    "findAll":true
}}

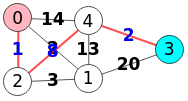
En la Figura vemos el resultado en Wolfram para ese grafo no dirigido con la misma función FindShortestPath[g, s, t, m], en este caso con s=1 y t=4 que se corresponde con los nodos "0" y "3" en nuestra aplicación, obteniéndose el mismo resultado.

g = WeightedAdjacencyGraph[{{∞,2,1,∞,14},{2,∞,3,20,13},{1,3,∞,∞,8},{∞,20,∞,∞,2},{14,13,8,2,∞}}, ImageSize -> 188, VertexSize -> {"Scaled", 0.17}, 
VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center], 3 -> Placed[2,Center], 4 -> Placed[3,Center], 5 -> Placed[4,Center]}, VertexLabelStyle -> Directive[Black,17.5], 
EdgeLabelStyle -> Directive[Black,17.5,Bold], EdgeLabels -> {(2->1)->2, (3->1)->1, (3->2)->3, (4->2)->20, (4->5)->2, (5->2)->13, (5->3)->8, (5->1)->14}, 
VertexStyle -> White, EdgeStyle -> {{Black,Thickness[0.005]}}];
f = FindShortestPath[g, 1, 4, Method -> "Dijkstra"];
p = PathGraph[f];
HighlightGraph[g,{Style[First[VertexList[p]], RGBColor["lightpink"]], Style[Last[VertexList[p]], If[First[VertexList[p]]!=Last[VertexList[p]], Cyan]],Style[EdgeList[p], Red, Thick], Annotation[EdgeList[p], EdgeLabelStyle->Directive[Blue,17.5,Bold]]}]

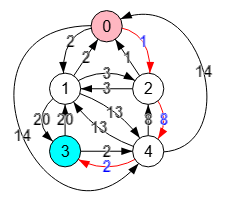
El motivo de que funcione el algoritmo en un grafo no dirigido es que podemos considerar cada arista "u-v" con un peso "w" no dirigida como la pareja "u🡒v" y "v🡒u" ambas con el mismo peso "w", como vemos en la Figura, grafo que consideramos como todo dirigido, con lo que el algoritmo tomará en consideración las aristas que forman camino desde el nodo raíz que se especifique al resto de los nodos.

{"nodes":[
    {"index":0,"nodeOffset":"25","parent":[{"index":-1},{"index":1,"lineType":"quadratic","value":2,"lineOffset":"-2 -2"},{"index":2,"lineOffset":"2 -2","value":1,"lineType":"quadratic"},{"index":4,"lineOffset":"-13 -5 -5 13","value":14,"lineType":"cubic"}]},
    {"index":1,"parent":[{"index":0,"value":2},{"index":2,"lineType":"quadratic","lineOffset":"0 -2","value":3},{"index":3,"lineType":"quadratic","lineOffset":-3,"value":20},{"index":4,"lineType":"quadratic","lineOffset":"1 -1","value":13}]},
    {"index":2,"parent":[{"index":0,"value":1},{"index":1,"value":3},{"index":4,"lineOffset":"2","lineType":"quadratic","value":8}]},
    {"index":3,"nodeOffset":"-16.67 50","parent":[{"index":1,"value":20},{"index":4,"value":2}]},
    {"index":4,"nodeOffset":"-8.33 50","parent":[{"index":1,"value":13,"lineType":"quadratic","lineOffset":"-1 1"},{"index":2,"value":8},{"index":0,"value":14,"lineOffset":"8 5 5 -8","lineType":"cubic"},{"index":3,"lineType":"quadratic","lineOffset":"0 2","value":2}]}
],
"config":{
    "markerEnd":"arrow",
    "algorithm":"Shortest path (Dijkstra)",
    "lastIndex":3
}}

El código JavaScript para ejecutar el algoritmo getShortestPathDijkstra() es el siguiente:

function getShortestPathDijkstra({matrix=[], firstIndex=0, lastIndex=0, findAll=false}){
    let result = {paths: [], pathLengths: [], pointers: []};
    try {
        let n = matrix.length;
        let edgeLengths = matrix.map((v,i) => v.map((w,j) => i===j ? 0 : w===0 ? Infinity : w));
        let pathLengths = matrix.map((v,i) => edgeLengths[firstIndex][i]);
        let candidates = matrix.map((v,i) => i).filter(v => v!==firstIndex);
        let pointers = matrix.map(() => firstIndex);
        let kPrev;
        // Greedy loop
        while (candidates.length>1) {
            if (iter++, iter>maxIter) return `Maximum iterations '${maxIter}' reached`;
            let k=null, min = Infinity;
            for (let j of candidates){
                if (pathLengths[j]<=min){
                    min = pathLengths[j];
                    k = j;
                }
            }
            if (k===null) return `Error k is null`;
            if (k===kPrev) return `Error k=${k} repeated`;
            kPrev = k;
            candidates = candidates.filter(v => v!==k);
            for (let j of candidates) {
                if (pathLengths[j] > pathLengths[k] + edgeLengths[k][j]){
                    pathLengths[j] = pathLengths[k] + edgeLengths[k][j];
                    pointers[j] = k;
                }
            }
        }
        result.pathLengths = pathLengths;
        result.pointers = pointers;
        // Build paths
        let lastIndices = findAll ? Array.from({length: n}, (v,i) => i) : [lastIndex];
        for (let index of lastIndices) {
            let path = [];
            if (Number.isFinite(pathLengths[index])) {
                let p = index;
                while (true) {
                    path.unshift(p);
                    if (p===firstIndex) break;
                    p = pointers[p];
                }
            }
            result.paths.push(path);
        }
    } catch(e) {result = e.message}
    return result;
}

Se basa en un algoritmo voraz, con el siguiente esquema con comentarios equiparándolo con el bucle while (candidates.length>1) con las variables edgeLenghts, pathLengths, candidates y pointers del código anterior:

function voraz(conjunto){ // conjunto ≡ edgeLengths y candidates
    let resultado = crear(conjunto); // resultado ≡  pathLenghts y pointers
    while (!esSolucion(resultado) && !esVacio(conjunto)){ // candidates.length > 1
        let candidato = seleccionar(conjunto); // seleccionar siguiente candidato k
        if (esCompletable(resultado, candidato)) { // siempre es completable
            resultado = guardar(resultado, candidato); // actualizar pathLengths y pointers
        }
    }
    return resultado; // pathLengths y pointers
}

El conjunto sobre el que aplicamos el algoritmo voraz son las longitudes de aristas edgeLengths y los candidatos son todos los vértices menos el raíz. El resultado que obtenemos al final del bucle son las longitudes de caminos pathLengths y los punteros pointers. La condición del bucle esSolucion(resultado) siempre es verdadera y con la condición !esVacio(conjunto) puede sustituirse por candidates.length > 1. El siguiente candidato se selecciona siempre de forma completable con el primer bucle for. Y guardar el resultado se realiza en el segundo bucle for actualizando pathLengths y pointers. La última parte para construir caminos (Build paths) no forma parte del voraz.

Algoritmo de Floyd para buscar los caminos mínimos en un grafo `getShortestPathFloyd()`

Ya traté este problema en el año 2020 en el tema algoritmo de Floyd caminos mínimos con ocasión de exponer un ejemplo de aplicación de programación dinámica. Ahora lo incorporo en la aplicación Grafos SVG con algunas mejoras.

Antes vimos el algoritmo de Dijkstra donde había que especificar un primer nodo y se encontraban los longitudes y punteros de caminos mínimos al resto de nodos. Si quisiéramos encontrar todos los caminos entre todos los nodos, habría que ejecutar este algoritmo de Dijkstra iterando el primer nodo por todos los nodos del grafo. El algoritmo de Floyd evita eso pues en una ejecución nos devuelve todos los resultados.

Como veremos en un ejemplo después, el algoritmo devuelve este resultado similar al de Dijkstra, pero ahora los caminos "paths", longitudes de caminos "pathLengths" y punteros "pointers" son matrices de n × n siendo n el número de nodos del grafo. Así la posición paths[1][4] = [1,2,4] contiene el camino mínimo entre los nodos "1" y "4" con longitud pathLengths[1][4] = 8.

Camino mínimo (Floyd) todos: {
"paths": [
    [[],[0,1],[0,2],[0,2,4,3],[0,2,4]],
    [[],[],[1,2],[1,2,4,3],[1,2,4]],
    [[],[],[],[2,4,3],[2,4]],
    [[],[],[],[],[]],
    [[],[],[],[4,3],[]]
],
"pathLengths":[
    [0,2,1,11,9],
    [Infinity,0,3,13,11],
    [Infinity,Infinity,0,10,8],
    [Infinity,Infinity,Infinity,0,Infinity],
    [Infinity,Infinity,Infinity,2,0]
],
"pointers":[
    [-1,0,0,4,2],
    [-1,-1,1,4,2],
    [-1,-1,-1,4,2],
    [-1,-1,-1,-1,-1],
    [-1,-1,-1,4,-1]
]

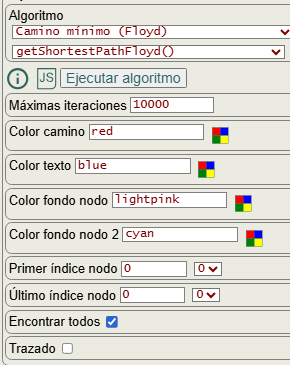
En la Figura vemos las opciones de algoritmo de Floyd. Si se marca la opción encontrar todos el resultado "paths" será una matriz como dijimos antes. Si está desmarcado entonces "paths" solo contendrá el camino entre primer índice nodo y último índice nodo, mientras que "pathLengths" y "pointers" serán iguales, pues el algoritmo siempre busca todas las longitudes de caminos y punteros.

A continuación vemos todos los caminos mínimos obtenidos con el algoritmo de Floyd del mismo grafo de ejemplo que hemos venido usando, recordando que en la aplicación se accede a cada grafo por medio de los botones de navegación que encontrará en la parte superior derecha del SVG.

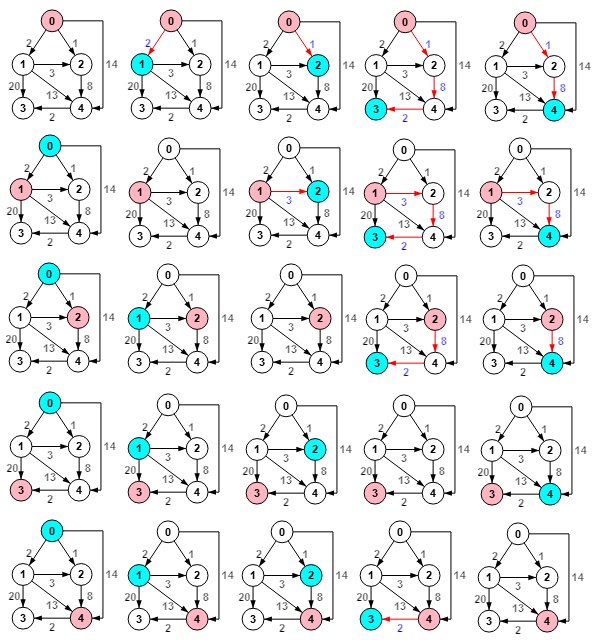
El color rosado del primer nodo y el azul del segundo se muestran en todos los casos, aunque no haya camino, menos para el camino al mismo nodo que sólo muestra el primer color. Este coloreado no forma parte del algoritmo y se aplica posteriormente a su ejecución.

Este es el resultado obtenido, observando que las posiciones paths[i][j] = [] supone que no hay camino entre "i,j", apareciendo entonces pathLengths[i][j] = Infinity.

Camino mínimo (Floyd) todos: {
"paths": [
    [[],[0,1],[0,2],[0,2,4,3],[0,2,4]],
    [[],[],[1,2],[1,2,4,3],[1,2,4]],
    [[],[],[],[2,4,3],[2,4]],
    [[],[],[],[],[]],
    [[],[],[],[4,3],[]]
],
"pathLengths":[
    [0,2,1,11,9],
    [Infinity,0,3,13,11],
    [Infinity,Infinity,0,10,8],
    [Infinity,Infinity,Infinity,0,Infinity],
    [Infinity,Infinity,Infinity,2,0]
],
"pointers":[
    [-1,0,0,4,2],
    [-1,-1,1,4,2],
    [-1,-1,-1,4,2],
    [-1,-1,-1,-1,-1],
    [-1,-1,-1,4,-1]
],
"trace":[]}

Con este JSON puede importar el ejemplo.

{"nodes":[
    {"index":0,"parent":[{"index":-1}]},
    {"index":1,"parent":[{"index":0,"value":2,"lineTextOffset":-0.8}]},
    {"index":2,"parent":[{"index":0,"value":1,"lineTextOffset":0.8},{"index":1,"value":3,"lineTextOffset":"0 0.8"}]},
    {"index":3,"parent":[{"index":1,"value":20,"lineTextOffset":-0.8},{"index":4,"value":2,"lineTextOffset":"0 0.8"}]},
    {"index":4,"parent":[{"index":1,"value":13,"lineTextOffset":"0 0.8"},{"index":2,"value":8,"lineTextOffset":0.8},{"index":0,"value":14,"lineOffset":"1","lineTextOffset":0.8}]}
],
"config":{
    "lineHeight":17.5,
    "nodeFontBold":true,
    "markerStart":"arrow",
    "algorithm":"Shortest path (Floyd)",
    "findAll":true
}}

A continuación vemos el mismo resultado en Wolfram usando la función FindShortestPath[g, s, t, m] para encontrar el camino mínimo entre "s" y "t" usando "All" en ambos casos pero con el método Dijkstra para "m", pues Wolfran no contempla Floyd. En el fondo Floyd es lo mismo que Dijkstra pero permite recuperar todos los caminos.

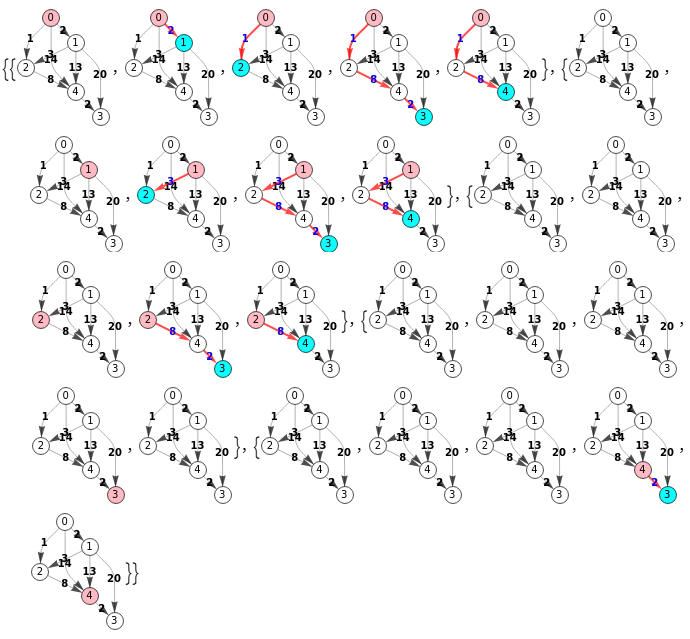
Por no liar más el código siguiente, no he aplicado los colores rosado y azul al primer y último nodo cuando no hay camino entre "u" y "v" y u≠v.

g = WeightedAdjacencyGraph[{{∞,2,1,∞,14},{∞,∞,3,20,13},{∞,∞,∞,∞,8},{∞,∞,∞,∞,∞},{∞,∞,∞,2,∞}}, ImageSize -> 95, VertexSize -> {"Scaled", 0.13}, 
VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center], 3 -> Placed[2,Center], 4 -> Placed[3,Center], 5 -> Placed[4,Center]}, 
VertexLabelStyle -> Directive[Black,10], EdgeLabelStyle -> Directive[Black,10,Bold], 
EdgeLabels -> {(1->2)->2, (1->3)->1, (2->3)->3, (2->4)->20, (5->4)->2, (2->5)->13, (3->5)->8, (1->5)->14}, 
VertexStyle -> White, DirectedEdges -> True, EdgeStyle -> {{Black,Thickness[0.005]}}];
f = FindShortestPath[g, All, All, Method -> "Dijkstra"];
t = Table[Table[PathGraph[f[i,j], DirectedEdges->True], {j, VertexList[g]}], {i, VertexList[g]}];
Table[Table[HighlightGraph[g,If[Length [VertexList[p]]>0,{ Style[First[VertexList[p]], RGBColor["lightpink"]], Style[Last[VertexList[p]], 
If[First[VertexList[p]]!=Last[VertexList[p]], Cyan]],Style[EdgeList[p],  Red, Thick], Annotation[EdgeList[p], EdgeLabelStyle->Directive[Blue,10,Bold]]}]], {p, q}], {q,t}]

Para el mismo grafo del ejemplo anterior desmarcamos la opción encontrar todos que vemos en la Figura, seleccionado "0" como primer índice nodo y "3" como último índice nodo y marcamos la opción trazado, obteniendo el camino mínimo [0, 2, 4, 3] que vemos en la Figura y el trazado que exponemos a continuación.

Ya explicamos este algoritmo en el tema algoritmo Floyd con un enfoque de programación dinámica, pero vamos a hacerlo nuevamente con esta traza. Es importante ver que Floyd hace lo mismo que Dijkstra, con la única ventaja de obtener en una ejecución todos los caminos mínimos del grafo con un enfoque basado en programación dinámica.

Tal como explicábamos en ese tema, la matriz longitudes de caminos (pathLengths) no es otra cosa que la tabla de resultados intermedios que veíamos en el tema sobre programación dinámica. En esa tabla está implícita la información para descubrir los caminos mínimos. Recordemos el principio de optimalidad que dice que en una secuencia de decisiones óptimas cualquier subsecuencia también es óptima.

Si observamos el grafo de la Figura, el camino óptimo "0" hasta "3" pasa por los nodos "2" y "4". Ese camino comprende los subcaminos "0→2", "2→4" y "4→3", subcaminos también óptimos.

INICIO:
pathLengths = [
  [0,2,1,∞,14]
  [∞,0,3,20,13]
  [∞,∞,0,∞,8]
  [∞,∞,∞,0,∞]
  [∞,∞,∞,2,0]
]
pointers = [
  [-1,0,0,-1,0]
  [-1,-1,1,1,1]
  [-1,-1,-1,-1,2]
  [-1,-1,-1,-1,-1]
  [-1,-1,-1,4,-1]
]

RESULTADOS INTERMEDIOS:

For {k,i,j} ∈ [0, 4] check pathLengths[i][k] + pathLengths[k][j] < pathLengths[i][j]
and if true update pathLengths[i][j] and pointers[i][j]

----------------------------------------------------------------------
For k=0 and {i,j} ∈ [0, 4]
check pathLengths[i][0] + pathLengths[0][j] < pathLengths[i][j]

----------------------------------------------------------------------
For k=1 and {i,j} ∈ [0, 4]
check pathLengths[i][1] + pathLengths[1][j] < pathLengths[i][j]

i=0 j=3
pathLengths[0][1]+pathLengths[1][3]<pathLengths[0][3] ⇒ 2+20<∞ ≡ true
pathLengths = [
  [0,2,1,22,14]
  [∞,0,3,20,13]
  [∞,∞,0,∞,8]
  [∞,∞,∞,0,∞]
  [∞,∞,∞,2,0]
]
pointers = [
  [-1,0,0,1,0]
  [-1,-1,1,1,1]
  [-1,-1,-1,-1,2]
  [-1,-1,-1,-1,-1]
  [-1,-1,-1,4,-1]
]

----------------------------------------------------------------------
For k=2 and {i,j} ∈ [0, 4]
check pathLengths[i][2] + pathLengths[2][j] < pathLengths[i][j]

i=0 j=4
pathLengths[0][2]+pathLengths[2][4]<pathLengths[0][4] ⇒ 1+8<14 ≡ true
pathLengths = [
  [0,2,1,22,9]
  [∞,0,3,20,13]
  [∞,∞,0,∞,8]
  [∞,∞,∞,0,∞]
  [∞,∞,∞,2,0]
]
pointers = [
  [-1,0,0,1,2]
  [-1,-1,1,1,1]
  [-1,-1,-1,-1,2]
  [-1,-1,-1,-1,-1]
  [-1,-1,-1,4,-1]
]

i=1 j=4
pathLengths[1][2]+pathLengths[2][4]<pathLengths[1][4] ⇒ 3+8<13 ≡ true
pathLengths = [
  [0,2,1,22,9]
  [∞,0,3,20,11]
  [∞,∞,0,∞,8]
  [∞,∞,∞,0,∞]
  [∞,∞,∞,2,0]
]
pointers = [
  [-1,0,0,1,2]
  [-1,-1,1,1,2]
  [-1,-1,-1,-1,2]
  [-1,-1,-1,-1,-1]
  [-1,-1,-1,4,-1]
]

----------------------------------------------------------------------
For k=3 and {i,j} ∈ [0, 4]
check pathLengths[i][3] + pathLengths[3][j] < pathLengths[i][j]

----------------------------------------------------------------------
For k=4 and {i,j} ∈ [0, 4]
check pathLengths[i][4] + pathLengths[4][j] < pathLengths[i][j]

i=0 j=3
pathLengths[0][4]+pathLengths[4][3]<pathLengths[0][3] ⇒ 9+2<22 ≡ true
pathLengths = [
  [0,2,1,11,9]
  [∞,0,3,20,11]
  [∞,∞,0,∞,8]
  [∞,∞,∞,0,∞]
  [∞,∞,∞,2,0]
]
pointers = [
  [-1,0,0,4,2]
  [-1,-1,1,1,2]
  [-1,-1,-1,-1,2]
  [-1,-1,-1,-1,-1]
  [-1,-1,-1,4,-1]
]

i=1 j=3
pathLengths[1][4]+pathLengths[4][3]<pathLengths[1][3] ⇒ 11+2<20 ≡ true
pathLengths = [
  [0,2,1,11,9]
  [∞,0,3,13,11]
  [∞,∞,0,∞,8]
  [∞,∞,∞,0,∞]
  [∞,∞,∞,2,0]
]
pointers = [
  [-1,0,0,4,2]
  [-1,-1,1,4,2]
  [-1,-1,-1,-1,2]
  [-1,-1,-1,-1,-1]
  [-1,-1,-1,4,-1]
]

i=2 j=3
pathLengths[2][4]+pathLengths[4][3]<pathLengths[2][3] ⇒ 8+2<∞ ≡ true
pathLengths = [
  [0,2,1,11,9]
  [∞,0,3,13,11]
  [∞,∞,0,10,8]
  [∞,∞,∞,0,∞]
  [∞,∞,∞,2,0]
]
pointers = [
  [-1,0,0,4,2]
  [-1,-1,1,4,2]
  [-1,-1,-1,4,2]
  [-1,-1,-1,-1,-1]
  [-1,-1,-1,4,-1]
]

CONSTRUIR CAMINOS
For i ∈ [0, 0], j ∈ [3, 3]
i = 0
    j = 3
        While pointer>-1
            pointer = pointers[i][j] = pointers[0][3] = 4
            path = [4]
            pointer = pointers[i][pointer] = pointers[0][4] = 2
            path = [2,4]
            pointer = pointers[i][pointer] = pointers[0][2] = 0
            path = [0,2,4]
            pointer = pointers[i][pointer] = pointers[0][0] = -1
        Add j=3 pathLengths[0][3] = 11 > 0 ⇒ path = [0,2,4,3]"}

INICIO:
pathLengths = [
  [0,2,1,∞,14]
  [∞,0,3,20,13]
  [∞,∞,0,∞,8]
  [∞,∞,∞,0,∞]
  [∞,∞,∞,2,0]
]
pointers = [
  [-1,0,0,-1,0]
  [-1,-1,1,1,1]
  [-1,-1,-1,-1,2]
  [-1,-1,-1,-1,-1]
  [-1,-1,-1,4,-1]
]

Veamos la parte INICIO de la traza anterior. Iniciamos las longitudes de caminos transformando la matriz de adyacencia con pesos que nos viene a la entrada del algoritmo con let pathLengths = matrix.map((v,i) => v.map((w,j) => i===j ? 0 : w===0 ? Infinity : w)), con un 0 en la diagonal cuando i===j e Infinity cuando no hay arista entre "i" y "j". En la traza se sustituye por "∞" para mayor legilibidad. En principio esa matriz refleja cada arista "u🡒v" con valor pathLengths[u][v], pero al final se convertirá en las longitudes de caminos de tal forma que pathLengths[u][v] será la distancia mínima que hay entre los nodos "u" y "v" pudiendo recorrer un camino de uno o más nodos.

La otra matriz que necesitamos son los punteros que formamos con let pointers = matrix.map((v,i) => v.map((w,j) => i===j || w===0 ? -1 : i)). Una posición pointers[u][v] = u significa que hay arista "u🡒v", en otro caso si es -1 es que no hay esa arista.

A partir de aquí se empieza a construir la tabla de resultados intermedios, con un triple bucle para {k,i,j} ∈ [0, 4]:

RESULTADOS INTERMEDIOS:

For {k,i,j} ∈ [0, 4] check pathLengths[i][k] + pathLengths[k][j] < pathLengths[i][j]
and if true update pathLengths[i][j] and pointers[i][j]

En la traza se hace la comprobación pathLengths[i][k] + pathLengths[k][j] < pathLengths[i][j] para todos los k, es decir, para todos los nodos del grafo, presentándose la actualización de la longitud de caminos pathLengths y los punteros pointers cuando se cumple esa condición. En esencia se trata de que en cada paso k extraemos la información del camino mínimo pathLengths_k[i][j] a partir de la información del paso anterior pathLenghts_k-1. Así si definimos C como la matriz de longitudes de caminos pathLengths. esa condición y la actualización viene a significar lo siguiente:

C_k[i][j] = Min(C_k-1[i][j], C_k-1[i][k] + C_k-1[k][j])

Se observa que para los nodos k=0 y k=3 no se producen actualizaciones:

For k=0 and {i,j} ∈ [0, 4]
check pathLengths[i][0] + pathLengths[0][j] <  pathLengths[i][j]
...
For k=3 and {i,j} ∈ [0, 4]
check pathLengths[i][3] + pathLengths[3][j] < pathLengths[i][j]

Para el nodo k=0 no hay aristas "i🡒0" que entren en el nodo "0" y por tanto pathLengths[i][0] = ∞, con lo que para cualquier valor de las aristas "0🡒j" e "i🡒j" sucede que ∞ + Distancia(0🡒j) no puede ser menor que Distancia(i🡒j). Vea que para un número a real cualesquiera, incluso infinito, ∞ + a = ∞ y si b ≠ ∞ entonces ∞ + a < b será falso, y si b = ∞ sucede que ∞ < ∞ será falso también (y también ∞ > ∞ pues sólo es cierto que ∞ = ∞). Para el nodo k=3 no hay aristas "3🡒j" que salgan del nodo "3", aplicándose el mismo planteamiento que antes con pathLengths[3][j] = ∞

Por lo tanto sólo los pasos de los nodos k con aristas entrantes y salientes producirán actualizaciones. Por ejemplo para el nodo k=1 tenemos:

For k=1 and {i,j} ∈ [0, 4]
check pathLengths[i][1] + pathLengths[1][j] < pathLengths[i][j]

i=0 j=3
pathLengths[0][1]+pathLengths[1][3]<pathLengths[0][3] ⇒ 2+20<∞ ≡ true
pathLengths = [
  [0,2,1,22,14]
  [∞,0,3,20,13]
  [∞,∞,0,∞,8]
  [∞,∞,∞,0,∞]
  [∞,∞,∞,2,0]
]

Vemos en las longitudes de caminos previa que Distancia(0🡒1) = 2, Distancia(1🡒3) = 20, Distancia(0🡒3) = ∞ así que 2+20 < ∞ es cierto, con lo que actualizamos pathLengths[0][3] = 22. Con esto si la longigud del camino "0,3" era inicialmente ∞ ahora hemos encontrado uno menor "0🡒1🡒3" con peso 22. Si seguimos la traza hasta k=4 i=0 j=3 veremos que tras encontrar el camino "0,4" mínimo con "0🡒2🡒4" y peso 9, ahora actualizamos el camino "0,3" con "0🡒2🡒4🡒3" y peso 11 menor que el anterior 22.

For k=4 and {i,j} ∈ [0, 4]
check pathLengths[i][4] + pathLengths[4][j] < pathLengths[i][j]

i=0 j=3
pathLengths[0][4]+pathLengths[4][3]<pathLengths[0][3] ⇒ 9+2<22 ≡ true
pathLengths = [
  [0,2,1,11,9]
  [∞,0,3,20,11]
  [∞,∞,0,∞,8]
  [∞,∞,∞,0,∞]
  [∞,∞,∞,2,0]

Siguiendo el proceso para el resto de nodos k al final tendremos pathLengths con la longitud mínima de caminos entre dos nodos cualesquiera del grafo y pointers que nos pemitirá reconstruir esos caminos. Este proceso es el mismo que hacíamos con el voraz en el algoritmo de Dijkstra que vimos en el apartado anterior. Allí sólo lo resolvíamos para un nodo k que era el primer índice de nodo que se pasaba al algoritmo. Ahora con Floyd hacemos lo mismo para todos los nodos.

La primera parte para construir los resultados intermedios se ejecuta siempre en cualquier caso para todos los nodos, aunque le solicitemos el algoritmo sólo el camino mínimo entre los nodos "0" y "3" como hicimos en esta traza, donde ahora la parte del trazado para construir caminos sólo devuelve la construcción del camino entre esos nodos:

CONSTRUIR CAMINOS
For i ∈ [0, 0], j ∈ [3, 3]
i = 0
    j = 3
        While pointer>-1
            pointer = pointers[i][j] = pointers[0][3] = 4
            path = [4]
            pointer = pointers[i][pointer] = pointers[0][4] = 2
            path = [2,4]
            pointer = pointers[i][pointer] = pointers[0][2] = 0
            path = [0,2,4]
            pointer = pointers[i][pointer] = pointers[0][0] = -1
        Add j=3 pathLengths[0][3] = 11 > 0 ⇒ path = [0,2,4,3]

La forma de construir caminos es similar a lo que vimos en Dijkstra. Si hay un puntero que no sea -1 vamos desferenciándolo y al final le agregamos el último nodo si es finitio y mayor que cero.

El JavaScript para ejecutar getShortestPathFloyd() se muestra a continuación, eliminando la parte del trazado:

function getShortestPathFloyd({matrix=[], firstIndex=0, lastIndex=0, findAll=false}){
    let result = {paths: [], pathLengths: [], pointers: []};
    try {
        let n = matrix.length;
        let pathLengths = matrix.map((v,i) => v.map((w,j) => i===j ? 0 : w===0 ? Infinity : w));
        let pointers = matrix.map((v,i) => v.map((w,j) => i===j || w===0 ? -1 : i));
        // Intermediate results
        for (let k=0; k<n; k++){
            for (let i=0; i<n; i++){
                for (let j=0; j<n; j++){
                    if (pathLengths[i][k] + pathLengths[k][j] < pathLengths[i][j]) {
                        pathLengths[i][j] = pathLengths[i][k] + pathLengths[k][j];
                        pointers[i][j] = pointers[k][j];
                    }
                }
            }
        }
        result.pathLengths = pathLengths;
        result.pointers = pointers;
        // Build paths
        let paths = [];
        let [ifrom, ito, jfrom, jto] = findAll ? [0, n-1, 0, n-1] : [firstIndex, firstIndex, lastIndex, lastIndex];
        for (let i=ifrom; i<=ito; i++){
            let pathsRow = [];
            for (let j=jfrom; j<=jto; j++){
                let path = [];
                let pointer = pointers[i][j];
                while (pointer > -1){
                    path.unshift(pointer);
                    pointer = pointers[i][pointer];
                }
                if (Number.isFinite(pathLengths[i][j]) && pathLengths[i][j]>0) path.push(j);
                pathsRow.push(path);
            }
            paths.push(pathsRow);
        }
        result.paths = findAll ? paths : paths[0];
    } catch(e) {result = e.message}
    return result;
}

No es más complejo que el que vimos de Dijkstra y poco más hay que explicar que ya no hayamos comentado.

Uso de caminos mínimos en otros algoritmos

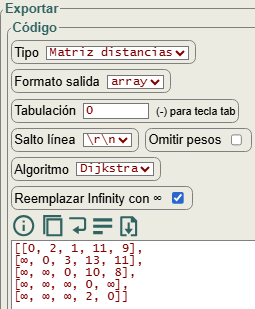
Usamos los algoritmos de Dijkstra o Floyd vistos antes en otras partes de la aplicación. En la Figura vemos que lo podemos usar para exportar el grafo en JSON a una matriz de distancias, que no es otra cosa que el resultado de la variable longitudes de caminos que hemos visto en este tema.

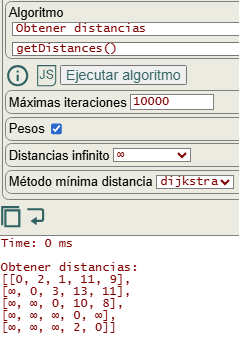
También para ejecutar el algoritmo getDistances() que nos devuelve la matriz de distancias a partir de una matriz de adyacencia de entrada, como se observa en la Figura.

Y para ejecutar el algoritmo findMaximumFlow() para encontrar el máximo flujo donde necesitamos encontrar un camino entre dos nodos, como se observa en la Figura, usándose findPath() pues no es necesario que el camino sea mínimo, pero también podemos usar el algoritmo de Dijkstra o Floyd que hemos visto en este tema.

Algoritmo de Dijkstra para buscar los caminos mínimos en un grafo getShortestPathDijkstra()

Algoritmo de Floyd para buscar los caminos mínimos en un grafo getShortestPathFloyd()

Uso de caminos mínimos en otros algoritmos

Algoritmo de Dijkstra para buscar los caminos mínimos en un grafo `getShortestPathDijkstra()`

Algoritmo de Floyd para buscar los caminos mínimos en un grafo `getShortestPathFloyd()`