Corte de aristas Stoer-Wagner
Encontrar corte mínimo aristas Stoer-Wagner findEdgeCutStoerWagner()
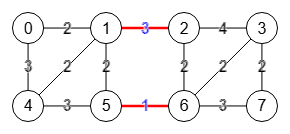
Encontrar un corte mínimo de aristas con el algoritmo de Stoer-Wagner en un grafo conectado y no dirigido con n nodos conlleva iterar n-1 veces identificando un corte en cada paso y almacenar el mínimo encontrado que, al final, será el mínimo del grafo.
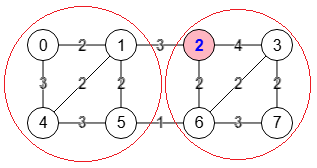
Se selecciona el nodo a=1 que se mantiene fijo en todos los pasos, que más abajo explicaremos el motivo de esa selección. En cada paso creamos un conjunto de vértices con ese nodo A=[1] y vamos agregando vértices restantes en el orden de los más fuertemente conectados con los vértices de A, quedando al final de esa lista los nodos "s" y "t", siendo "t" el menos fuertemente conectado. Esto nos permite obtener un corte parcial de "t" con respecto al resto con un cierto peso entre ambos componentes. Iremos almacenando siempre el menor de todos los cortes parciales que nos servirá al final para obtener el corte mínimo del grafo. En cada paso contraemos los nodos "t" y "s" y el grafo contraído servirá de base para el siguiente paso. Cuando lleguemos al paso n-1 el grafo contraído tendra 2 nodos y habremos finalizado estos pasos, tras lo cual recuperamos el corte mínimo almacenado que será el que se devuelva.
Find edge cut Stoer-Wagner: {
"edges":[[2,1],[6,5]],
"weight":4,
"a":1,
"components":[[2,3,6,7],[0,4,1,5]],
"trace":[]}Este es el resultado obtenido del grafo de la Figura, ejemplo que puede encontrar en Wikipedia y que también forma parte del documento original A Simple Min-Cut Algorithm de Stoer y Wagner. El corte mínimo tiene un peso 4 y lo conforman las aristas [[2,1],[6,5]], separando el grafo en dos componentes [[2,3,6,7],[0,4,1,5]]. Decimos 2 componentes y no más pues este algoritmo se aplica a grafos conectados, así que el corte mínimo producirá 2 componentes conectados.
Además el algoritmo sólo se aplica a grafos no dirigidos. Podemos forzar no dirigido con la opción para ejecutar el algoritmo que vemos en la Figura. La opción trazado nos devuelve una traza con los pasos seguidos que expondremos a continuación. Las opciones color camino y color texto no pertenecen al algoritmo y sirven para, posteriormente a su ejecución, presentar el resultado en pantalla.
Con el siguiente JSON puede importar ese ejemplo.
{"nodes":[
{"index":0,"nodeOffset":"-38.75 -1.25","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"9.17 -26.25","parent":[{"index":0,"value":2}]},
{"index":2,"nodeOffset":"40.42 -51.25","parent":[{"index":1,"value":3}]},
{"index":3,"nodeOffset":"71.67 -76.25","parent":[{"index":2,"value":4}]},
{"index":4,"nodeOffset":"-55.42 5","parent":[{"index":0,"value":3},{"index":1,"value":2}]},
{"index":5,"nodeOffset":"-24.17 -20","parent":[{"index":1,"value":2},{"index":4,"value":3}]},
{"index":6,"nodeOffset":"7.08 -45","parent":[{"index":2,"value":2},{"index":5,"value":1},{"index":3,"value":2}]},
{"index":7,"nodeOffset":"55 -70","parent":[{"index":3,"value":2},{"index":6,"value":3}]}
],
"config":{
"algorithm":"Find edge cut Stoer-Wagner"
}}
Veamos ahora el trazado de todos los pasos hasta llegar al resultado final. Al inicio tendremos el grafo de la Figura donde seleccionamos el nodo a=1, selección que se mantendrá en todo el algoritmo. Como iremos contrayendo el grafo hasta quedar dos nodos y como hay que mantener el mismo índice de "a" entonces o es cero o uno con objeto de que con el último grafo con dos nodos el índice sea correcto. Usamos 1 pues es el que selecciona el ejemplo del documento de los autores Stoer y Wagner aunque también podría ser 0. Aunque hay que advertir que en ese documento A Simple Min-Cut Algorithm de Stoer y Wagner seleccionan a=2 pues los nodos se inician en 1 en lugar de 0 y en nuestros algoritmos todos los grafos siempre se inician en 0. Todos los pasos que veremos a continuación coinciden exactamente con los de ese documento.
{"step":1,"s":4,"t":0,
"vertexs":[1,2,3,6,7,5,4,0],
"labels":[[0,4],[1],[2],[3],[5],[6],[7]],
"labelsAccumulated":[[0,4],[1],[2],[3],[5],[6],[7]],
"weight":5,"stepMin":1,"minWeight":5,
"matrix":
[[0,4,0,0,3,0,0],
[4,0,3,0,2,0,0],
[0,3,0,4,0,2,0],
[0,0,4,0,0,2,2],
[3,2,0,0,0,1,0],
[0,0,2,2,1,0,3],
[0,0,0,2,0,3,0]]}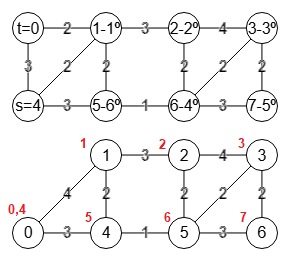
En el paso 1 construimos la lista de nodos "A" (vertexs en la traza anterior) iniciándose con A=[1], siendo el primero en orden "1-1º" como se observa en el grafo superior de la Figura. Se trata de ir agregando al conjunto A el resto de vértices siguiendo el orden de los mas fuertemente conectados primero.
De los tres nodos del grafo anterior de la Figura adyacentes a A=[1] que son 0,2,5 es el nodo "2" el que tiene una arista con mayor peso 3, con lo que A=[1,2]. De todas las aristas que inciden en A=[1,2] es el nodo 3 el que tiene las aristas incidentes con mayor peso, una en este caso 3-2 con peso 4, así que agregamos el nodo "3" quedando A=[1,2,3]. El siguiente es "6" pues tiene dos aristas incidentes en A=[1,2,3] con pesos 2+2=4 mayor que el resto de nodos, con lo que A=[1,2,3,6]. Seguimos ordenando de esta forma hasta que A=[1,2,3,6,7,5,4,0]. Los dos últimos nodos son s=4 y t=0 quedando este orden como el grafo superior de la Figura. Esa lista está ordenada por el grado de conexión de los pesos con lo que el último nodo t=0 es el más débilmente conectado y supone un corte mínimo de fase o parcial.
En ese grafo observamos el nodo t=0 con las dos aristas 0-1 y 0-4 con suma de pesos 2+3=5, guardando en cada paso el peso mínimo del corte de fase que separa "t" del resto comparándolo con los cortes previos. Finalmente en este paso contraemos los nodos t=0 y s=4 quedando como el grafo inferior de la Figura. Los números en color rojo son las correspondencias con los vértices del grafo inicial de la Figura.
En la traza de este paso 1 vemos los nodos s=4, t=0, el conjunto A en "vertexs", las etiquetas "labels" finales del grafo contraído, las etiquetas acumuladas "labelsAccumulated" con la correspondencia con el grafo inicial, ambas iguales por ser el primer paso, el peso "weight" del corte de fase o parcial t=0 siendo el mínimo pues es el primer paso y, finalmente, la matriz de adyacencia del grafo contraído.
{"step":2,"s":5,"t":6,
"vertexs":[1,0,4,2,3,5,6],
"labels":[[0],[1],[2],[3],[4],[5,6]],
"labelsAccumulated":[[0,4],[1],[2],[3],[5],[6,7]],
"weight":5,"stepMin":1,"minWeight":5,
"matrix":
[[0,4,0,0,3,0],
[4,0,3,0,2,0],
[0,3,0,4,0,2],
[0,0,4,0,0,4],
[3,2,0,0,0,1],
[0,0,2,4,1,0]]}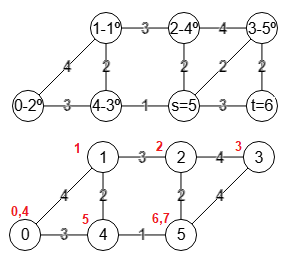
En el paso 2 partimos del grafo contraído en el paso anterior y componemos el conjunto A=[1] con resto de vértices, resultando A=[1,0,4,2,3,5,6] que puede ver en "vertexs" de la traza, quedando s=5 y t=6, tal como se observa en el grafo superior de la Figura. Las dos aristas 3-6 y 5-6 tiene suma de pesos 2+3=5 no siendo mayor que el peso de corte del paso anterior, por lo que en la traza seguimos manteniendo "stepMin":1 y "minWeight":5 del paso 1 anterior.
Contraemos t=6 y s=5 quedando como el grafo inferior de la Figura, siendo "labels" las etiquetas de este grafo contraído correspondiéndose con el de antes de contraer, y "labelsAccumulated" la correspondencia con respecto al grafo inicial, señalándose en color rojo en la Figura. La matriz de adyacencia de la traza es la del grafo contraído que servirá de base al siguiente paso.
{"step":3,"s":3,"t":5,
"vertexs":[1,0,4,2,3,5],
"labels":[[0],[1],[2],[3,5],[4]],
"labelsAccumulated":[[0,4],[1],[2],[3,6,7],[5]],
"weight":7,"stepMin":1,"minWeight":5,
"matrix":
[[0,4,0,0,3],
[4,0,3,0,2],
[0,3,0,6,0],
[0,0,6,0,1],
[3,2,0,1,0]]}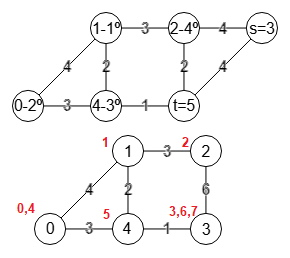
En el paso 3 y tomando como base el grafo contraído anterior, componemos A=[1] agregando el resto de vértices quedando A=[1,0,4,2,3,5] como se observa en "vertexs" de la traza y en el grafo superior de la Figura. Vemos que s=3 y t=5, siendo el peso de este corte la suma de 1+2+4=7 de las aristas 4-5, 2-5 y 3-5, siendo un peso mayor que el mínimo registrado antes "stepMin":1, "minWeight":5 quedando ese como mínimo hasta el momento.
Contraemos t=5 y s=3 quedando como el grafo inferior de la Figura con los números en rojo siendo la correspondencia con los vértices del grafo inicial y que vemos en "labelsAccumulated" de la traza.
{"step":4,"s":2,"t":3,
"vertexs":[1,0,4,2,3],
"labels":[[0],[1],[2,3],[4]],
"labelsAccumulated":[[0,4],[1],[2,3,6,7],[5]],
"weight":7,"stepMin":1,"minWeight":5,
"matrix":
[[0,4,0,3],
[4,0,3,2],
[0,3,0,1],
[3,2,1,0]]}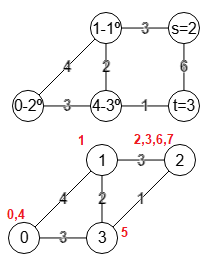
En el paso 4 tomando como base el grafo contraído en el paso anterior componemos A=[1,0,4,2,3] que puede observar en "vertexs" de la traza y en el grafo superior de la Figura. Vemos que s=2 y t=3, siendo el peso del corte 1+6=7 de las aristas 4-3 y 2-3, que también es mayor que el mínimo registrado "stepMin":1,"minWeight":5 del primer paso. Contraemos s=2 y t=3 quedando como el grafo inferior de la Figura con las etiquetas en correspondencia con el grafo inicial en color rojo obtenidas desde "labelsAccumulated" de la traza.
{"step":5,"s":3,"t":2,
"vertexs":[1,0,3,2],
"labels":[[0],[1],[2,3]],
"labelsAccumulated":[[0,4],[1],[2,3,6,7,5]],
"weight":4,"stepMin":5,"minWeight":4,
"matrix":
[[0,4,3],
[4,0,5],
[3,5,0]]}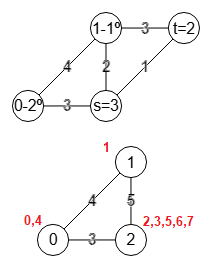
En el paso 5 partimos del grafo contraido en el paso anterior y conformamos A=[1,0,3,2] que puede ver en el grafo superior de la Figura y en "vertexs" de la traza. Vemos que s=3 y t=2, con el peso de este corte 3+1=4 de las aristas 1-2 y 3-2, siendo este peso 4 menor que el mínimo registrado que era 5, pasando a ser el peso de este corte ahora el mínimo "stepMin":5,"minWeight":4. En estos casos de peso mínimo se almacenan los datos t=2 y "labelsAccumulated" = [[0,4],[1],[2,3,6,7,5]] que son las etiquetas iniciales del grafo contraído en el paso anterior de donde se toma el nuevo peso mínimo 4, pues cuando finalicemos con un grafo contraído con dos nodos obtendremos el corte mínimo del grafo inicial a partir de esos datos. Contraemos t=2 y s=3 quedando como el grafo inferior de la Figura.
{"step":6,"s":2,"t":0,
"vertexs":[1,2,0],
"labels":[[0,2],[1]],
"labelsAccumulated":[[0,4,2,3,6,7,5],[1]],
"weight":7,"stepMin":5,"minWeight":4,
"matrix":[[0,9],[9,0]]}
En el paso 6 partimos del grafo contraido en el paso anterior componiendo A=[1,2,0] como se observa en el grafo superior de la Figura y en "vertexs" de la traza. Ahora s=2 y t=0, siendo el peso de corte 4+3=7 de las aristas 1-0 y 2-0, siendo mayor que el anterior mínimo "stepMin":5, "minWeight":4 del paso 5 permaneciendo como mínimo.
Contraemos t=0 y s=2 quedando finalmente un grafo con dos nodos como vemos en el inferior de la Figura. Observe que el nodo a=1 permanece independiente durante todo el proceso y que el resto de nodos se han contraído en un único nodo. Como el grafo contraído tiene 2 nodos habremos finalizado el proceso.
En el paso 5 habíamos encontrado un corte de fase o parcial mínimo con los datos t=2 y "labels"=[[0,4],[1],[2,3,6,7],[5]] que recordamos que eran los vértices del grafo contraido en el paso anterior 4 en el campo "labelsAccumulated". Buscamos 2 en "labels" y vemos que es el subconjunto [2,3,6,7] siendo un componente conectado del corte y el resto de vértices será el otro componente, como se observa en la Figura y en los campos "set1" y "set2" de la traza de este paso final que vemos a continuación:
{"t":2,
"labels":[[0,4],[1],[2,3,6,7],[5]],
"labelsAccumulated":[[0,4,2,3,6,7,5],[1]],
"set1":[2,3,6,7],
"set2":[0,4,1,5]}El corte mínimo final del grafo inicial son todas las aristas que comparten esos dos componentes, observando que son 1-2 y 5-6 con peso 3+1=4 como vemos en la Figura, devolviéndose esas aristas "edges":[[2,1],[6,5]] como vimos en el resultado del algoritmo al inicio de este apartado y que exponemos otra vez:
Find edge cut Stoer-Wagner: {
"edges":[[2,1],[6,5]],
"weight":4,
"a":1,
"components":[[2,3,6,7],[0,4,1,5]],
"trace":[]}El campo "labelsAccumulated" en la traza del paso final es la del último grafo contraído con dos nodos que en este ejemplo no la necesitamos para nada pero que servirá para un caso como el que expondremos en el siguiente apartado. Observe que en el resultado ponemos "a"=1 que es el vértice seleccionado al inicio y que permanece invariable en todo el proceso.
Consideraciones sobre la selección del vértice a=1
El último grafo contraído con dos nodos siempre finaliza con dos componentes conectados, uno de ellos con el único nodo [a] recordando que a=1 era el nodo inicialmente seleccionado y otro componente con el resto de nodos del grafo inicial. Dado que ese último grafo contraído tiene sólo 2 nodos es por lo que "a=0" o "a=1". Optamos por "a=1" pues es el que utiliza los autores Stoer y Wagner en su documento. Incluso dice que "a" puede ser cualquier nodo del grafo contraído previamente, pero en las pruebas que he realizado no he conseguido que funcionara adecuadamente. Aún hay algo más relacionado con la selección de "a" que veremos a continuación y que no me queda del todo claro.
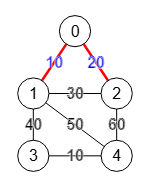
Finalmente optando por a=1 fijo en todas las fases, como ejemplo vemos el grafo de la Figura obteniendo el corte [[0,1],[0,2]] con peso 30, que visualmente se verifica que es el corte mínimo.
Find edge cut Stoer-Wagner: {
"edges":[[0,1],[0,2]],
"weight":30,
"a":1,
"components":[[0],[1,2,3,4]]
"trace":[]}En el resultado vemos los dos componentes del corte "components":[[0],[1,2,3,4]] con peso "weight":30 y a continuación se muestra la traza de la ejecución.
[{"step":1,"s":3,"t":0,"vertexs":[1,4,2,3,0],
"labels":[[0,3],[1],[2],[4]],"labelsAccumulated":[[0,3],[1],[2],[4]],
"weight":30,"stepMin":1,"minWeight":30,
"matrix":[[0,50,20,10],[50,0,30,50],[20,30,0,60],[10,50,60,0]]},
{"step":2,"s":3,"t":2,"vertexs":[1,0,3,2],
"labels":[[0],[1],[2,3]],"labelsAccumulated":[[0,3],[1],[2,4]],
"weight":110,"stepMin":1,"minWeight":30,
"matrix":[[0,50,30],[50,0,80],[30,80,0]]},
{"step":3,"s":2,"t":0,"vertexs":[1,2,0],
"labels":[[0,2],[1]],"labelsAccumulated":[[0,3,2,4],[1]],
"weight":80,"stepMin":1,"minWeight":30,
"matrix":[[0,130],[130,0]]},
{"t":0,
"labels":[[0],[1],[2],[3],[4]],
"labelsAccumulated":[[0,3,2,4],[1]],
"set1":[0],"set2":[1,2,3,4]}]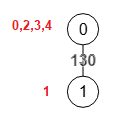
El último grafo contraído es el de la Figura importada desde la matriz del último paso, con dos nodos con los componentes de "labelsAccumulated": [[0,3,2,4],[1]] donde a=1 es uno de los componentes que no puede ser un corte mínimo del grafo, pues la suma de sus aristas 0-1, 2-1, 4-1 y 3-1 con pesos 10+30+50+40=130 es superior al peso 30 del corte [[0],[1,2,3,4]] obtenido. Pero en algún caso pudiera no ser así como veremos en el siguiente ejemplo.
{"nodes":[
{"index":0,"parent":[{"index":-1}]},
{"index":1,"parent":[{"index":0,"value":10}]},
{"index":2,"parent":[{"index":0,"value":20},{"index":1,"value":30}]},
{"index":3,"parent":[{"index":1,"value":40},{"index":4,"value":10}]},
{"index":4,"parent":[{"index":1,"value":50},{"index":2,"value":60}]}
],
"config":{
"nodeOffset":"-20",
"algorithm":"Find edge cut Stoer-Wagner"
}}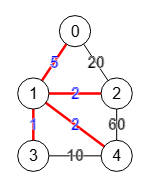
Este grafo es igual al anterior con menor peso en las aristas incidentes en a=1.
Find edge cut Stoer-Wagner: {
"edges":[[1,0],[1,2],[1,3],[1,4]],
"weight":10,
"a":1,
"components":[[0,2,3,4],[1]]
"trace":[]}Separar el nodo a=1 en los componentes [[0,2,3,4],[1]] tiene un peso 5+2+2+1=10, menor que cualquier otro corte. Y esos componentes son los que vemos resaltados en el campo "labelsAccumulated": [[0,2,3,4],[1]] del paso 3 y paso final de la traza siguiente:
[{"step":1,"s":4,"t":3,"vertexs":[1,0,2,4,3],
"labels":[[0],[1],[2],[3,4]],"labelsAccumulated":[[0],[1],[2],[3,4]],
"weight":11,"stepMin":1,"minWeight":11,
"matrix":[[0,5,20,0],[5,0,2,3],[20,2,0,60],[0,3,60,0]]},
{"step":2,"s":2,"t":3,"vertexs":[1,0,2,3],
"labels":[[0],[1],[2,3]],"labelsAccumulated":[[0],[1],[2,3,4]],
"weight":63,"stepMin":1,"minWeight":11,
"matrix":[[0,5,20],[5,0,5],[20,5,0]]},
{"step":3,"s":0,"t":2,"vertexs":[1,0,2],
"labels":[[0,2],[1]],"labelsAccumulated":[[0,2,3,4],[1]],
"weight":25,"stepMin":1,"minWeight":11,
"matrix":[[0,10],[10,0]]},
{"t":3,
"labels":[[0],[1],[2],[3],[4]],
"labelsAccumulated":[[0,2,3,4],[1]],
"weightB":10,
"edgesB":[[1,0],[1,2],[1,3],[1,4]]}]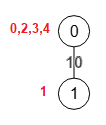
Así que al finalizar siempre hemos de comprobar si el nodo a=1 es uno de los dos componentes de un posible corte mínimo del grafo, como en este ejemplo que en el último grafo contraído vemos los componentes "labelsAccumulated": [[0,2,3,4],[1]] con un peso de corte 10, como vemos en la Figura importada desde la última matriz del tercer paso. Si no hiciéramos eso devolvería el seleccionado "stepMin":1, "minWeight":11 en el primer paso, que se corresponde con el corte [[3],[0,1,2,4]] que tiene un peso de 1+10=11 superior.
{"nodes":[
{"index":0,"parent":[{"index":-1}]},
{"index":1,"parent":[{"index":0,"value":5}]},
{"index":2,"parent":[{"index":0,"value":20},{"index":1,"value":2}]},
{"index":3,"parent":[{"index":1,"value":1},{"index":4,"value":10}]},
{"index":4,"parent":[{"index":1,"value":2},{"index":2,"value":60}]}
],
"config":{
"nodeOffset":"-20",
"algorithm":"Find edge cut Stoer-Wagner"
}}Algoritmo findEdgeCutStoerWagner()
function findEdgeCutStoerWagner({matrix=[], forceUndirected=false}){
let result = {edges: [], weight: 0, a:-1, components: null}, temp;
try {
let directed = isGraphDirected({matrix});
if (typeof directed==="string") throw new Error(directed);
if (directed) {
if (!forceUndirected) {
throw new Error(`The graph is directed and should be applied to undirected graphs or use the force undirected option`);
} else {
if (temp = operateDirectionGraph({matrix, edgesDirection:"undirected"}), temp.error) throw new Error(temp.error);
matrix = temp.matrix;
}
}
if (temp = isGraphConnected({matrix, forceUndirected:true}), typeof temp==="string") throw new Error(temp);
if (!temp) throw new Error(`The graph is not connected`);
if (temp = getMatrixModeValue({matrix}), typeof temp==="string") throw new Error(temp);
let [modeValue, nullValue] = temp;
let n = matrix.length;
let matrixCopy = JSON.parse(JSON.stringify(matrix));
if (["null/value", "false/true"].includes(modeValue)) {
for (let i=0; i<n; i++) {
matrixCopy[i][i] = 0;
for (let j=i+1; j<n; j++) {
if (matrixCopy[i][j]!==nullValue) {
matrixCopy[i][j] = 1;
matrixCopy[j][i] = 1;
} else {
matrixCopy[i][j] = 0;
matrixCopy[j][i] = 0;
}
}
}
}
let matrixReserve = JSON.parse(JSON.stringify(matrixCopy));
function minimumCutPhase({matrix=[], a=0}){
let n = matrix.length;
if (temp = getEdges({matrix:matrixCopy, edgesCompact:true, modeValue:"0/number"}), typeof temp==="string") throw new Error(temp);
let edges = temp;
let vertexs = [a];
let candidates = Array.from({length: n}, (v,i) => i).filter(v => v!==a);
let weight = 0;
while (candidates.length>0){
let maxVertex = -1;
let maxWeight = -1;
for (let vertex of candidates) {
let sumWeight = 0;
let edgesFilter = edges.filter(v => v[0]===vertex && vertexs.includes(v[1]) || v[1]===vertex && vertexs.includes(v[0]));
if (edgesFilter.length>0){
for (let edge of edgesFilter) {
let [i,j] = edge;
sumWeight += matrix[i][j];
}
if (sumWeight > maxWeight){
maxWeight = sumWeight;
weight = maxWeight;
maxVertex = vertex;
}
}
}
if (maxVertex===-1) throw new Error("maxVertex = -1");
vertexs.push(maxVertex);
let k = candidates.findIndex(v => v===maxVertex);
if (k===-1) throw new Error("k=-1")
candidates.splice(k, 1);
}
if (vertexs.length!==n) throw new Error("vertex.length!==n");
let s = vertexs[n-2];
let t = vertexs[n-1];
if (temp = operateContractionGraph({matrix, index1:t, index2:s, typeMergedValue:"sum", omitSelfLoops:true}), temp.error) throw new Error("(operateContractionGraph) " + temp.error);
matrix = temp.matrix;
let labels = temp.labels;
let arrReturn = [t, weight, labels, matrix];
return arrReturn;
}
function minimumCut({matrix=[]}){
let labelsAccumulated = Array.from({length: matrix.length}, (v,i) => [i]);
let min = {t:-1, weight:Infinity, labels:null, labelsAccumulated: null};
let a = 1;
result.a = a;
while (matrix.length>2) {
let t, weight, labels;
[t, weight, labels, matrix] = minimumCutPhase({matrix, a});
let tt = labelsAccumulated.findIndex(v => v.includes(t));
if (tt===-1) throw new Error("tt=-1");
if (weight<min.weight) {
min.weight = weight;
min.t = tt;
min.labels = JSON.parse(JSON.stringify(labelsAccumulated));
}
let arr = [];
for (let label of labels) {
arr.push(label.map(v => labelsAccumulated[v]).flat());
}
labelsAccumulated = arr;
min.labelsAccumulated = arr;
min.weightEnd = weight;
}
return min;
}
if (n>2) {
let min = minimumCut({matrix:matrixCopy});
let {t, weight, labels, labelsAccumulated} = min;
let weightB = 0;
let edgesB = []
let [b, arr] = labelsAccumulated[0].length===1 ? [labelsAccumulated[0][0], labelsAccumulated[1]] : [labelsAccumulated[1][0], labelsAccumulated[0]];
for (let i of arr) {
if (matrixReserve[b][i]>0) {
weightB += matrixReserve[b][i];
edgesB.push([b,i]);
}
}
if (weightB<weight) {
result.components = labelsAccumulated;
result.edges = edgesB;
result.weight = weightB;
} else {
let set1 = labels[t];
let set2 = labels.toSpliced(t, 1).flat();
result.components = [set1, set2];
for (let i of set1){
for (let j of set2) {
if (matrixReserve[i][j]!==0){
result.edges.push([i, j]);
}
}
}
result.weight = weight;
}
} else if (n===2) {
result.components = [[0], [1]];
result.edges.push([0,1]);
result.weight = matrixReserve[0][1];
}
} catch(e) {result = e.message}
return result;
}El algoritmo es una implementación del esquema que puede verser en Wikipedia y que procede del documento original A Simple Min-Cut Algorithm de Stoer y Wagner. El siguiente esquema en pseudocódigo es esa implementación:
M = matriz adyacencia ponderada de un grafo con n vértices
FUNCIÓN ACCESORIA PARA ENCONTRAR UN CORTE PARCIAL
Función minimumCutPhase(M, a)
A = [a]
Mientras A tenga menos de n vértices
Encontrar el vértice más fuertemente conectado
Agregar a A ese vértice
Fin Mientras
s,t son los dos últimos vértices de A
w es el peso de t con respecto a A
M,L = Contraer M con t y s
L son las etiquetas del grafo contraído con correspondencia con el original
Devolver M,L,t,w
Fin Función
FUNCIÓN ACCESORIA PARA ENCONTRAR EL CORTE MÍNIMO
Función minimumCut(M)
a = 1
minW es el peso mínimo
minT es el menor vértice de corte
minL es el etiquetado del menor corte
Mientras M tenga más de 2 nodos
M,L,t,w = minimumCutPhase(M, a)
Si w < minW entonces
minW = w
minT = t
minL = L
Fin si
Fin Mientras
Devolver M,minL,minT,minW
Fin Función
CUERPO PRINCIPAL DEL ALGORITMO
C = copia del grafo original M
Si n>2 entonces
M,L,minT,minW = minimumCut(M)
w = peso de corte de a=1
Si w<minW entonces
E = Obtener desde C aristas que cortan a=1
Devolver E
en otro caso
S1,S2 = Obtener componentes desde L y minT
E = Obtener desde C las aristas de corte entre S1 y S2
Devolver E
Fin Si
en otro caso si n=2
E = Arista de corte entre los dos nodos de C
Devolver E
en otro caso
No hay corte pues no hay aristas
Fin SiEn el algoritmo se usan las siguientes operaciones o algoritmos:
isGraphDirected()para saber si el grafo es dirigido pues Stoer-Wagner solo puede aplicar a grafos no dirigidos.operateDirectionGraph()para convertir en no dirigido un grafo dirigido en caso de que se establezca el argumentoforceUndirecteda verdadero.isGraphConnected()para saber si el grafo es conectado pues Stoer-Wagner solo puede aplicarse a grafos conectados.getMatrixModeValue()para obtener el modo valores de la matriz que puede ser "0/number", "0/1 ", "null/value" y "false/true", convirtiendo los dos últimos en el modo "0/1".getEdges()para obtener las aristas desde una matriz de adyacencia.operateContractionGraph()para contraer un grafo.
En el JavaScript hasta la línea function minimumCutPhase es el código que revisa que el grafo sea no dirigido y conectado y que la matriz de adyacencia sólo tenga ceros y números no negativos como los de un grafo ponderado.
Se declaran las dos funciones interiores minimumCutPhase() y minimumCut() y a continuación vemos el cuerpo principal de ejecución. Con el pseudocódigo anterior más lo que hemos explicado en la traza de los apartados anteriores creo que es suficiente para entenderlo.
Comparando algoritmos para encontrar corte mínimo de aristas

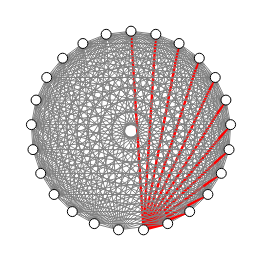
En la Figura vemos un grafo que hemos modificado a partir del grafo completo K12 con 12 nodos, donde cada nodo tiene aristas a los 11 restantes, pero que al nodo 5 le hemos eliminado 6 aristas a los nodos siguientes 6 a 11. Así que el corte mínimo serán las aristas del nodo 5 a los 5 nodos anteriores, como se observa en la Figura separando el nodo 5 del resto de nodos.
Vamos a comparar varios algoritmos ejecutándose para encontrar ese único corte de peso mínimo 5, pues el resto de cortes son de peso 11.
| Algoritmo | Tiempo ms | Iteraciones máximas | Permite dirigidos | Permite desconectados | Devuelve otros cortes |
|---|---|---|---|---|---|
| Corte aristas | 9170 | 50 000 000 | Sí | Sí | Sí, todos los cortes |
| Gomory-Hu | 3768 | 8 000 000 | No | No | Sí, todos los cortes mínimos |
| Karger | 10 | 10000 | No | No | No, sólo el primer mínimo que encuentre |
| Karger-Stein | 10 | 10000 | No | No | No, sólo el primer mínimo que encuentre |
| Stoer-Wagner | 1 | 10000 | No | No | No, sólo el primer mínimo que encuentre |
Ejecutamos los algoritmos que hemos visto en temas anteriores y este tema con este grafo obteniendo el mismo resultado de la Figura y los resultados de esta tabla. Hemos anotado el mínimo de tiempos en varias ejecuciones, ordenándolos por ese tiempo.
El primero es el corte aristas findEdgeCut() que se basa en iterar por todas las parejas de nodos "s" y "t" del grafo aplicando findSTEdgeCut() con objeto de recopilar todos los cortes posibles, ordenándolos al final de menor a mayor peso. Obviamente esto es una carga de ejecución importante cuando el grafo empieza a tener más de 10 nodos, pues con 10 nodos hay que ejecutar C(10, 2) = 45 veces findSTEdgeCut() y con 25 nodos hay que ejecutarlo C(25, 2) = 300 veces. Eso supone que por encima de 10 nodos sea poco eficiente. Sin embargo una ventaja de este algoritmo es que permite aplicarlo a grafos dirigidos y desconectados y devuelve todos los cortes.
El algoritmo Gomory-Hu necesita casi 4 segundos, de los que para la construcción previa de ese árbol Gomory-Hu se lleva unos 2 segundos. El resto se invierte en buscar las aristas con menor peso en el árbol y aplicar findSTEdgeCut() a los dos nodos de esas aristas, aunque para este ejemplo sólo hay una arista del árbol con corte mínimo.
Usar findSTEdgeCut() para encontrar el corte mínimo no es muy eficiente. Por eso los otros algoritmos que no lo usan son más eficientes.
Con este JSON se importa el ejemplo anterior.
{"nodes":[
{"index":0,"nodeOffset":"2.5","parent":-1},
{"index":1,"nodeOffset":"64.17 -19.64","parent":0},
{"index":2,"nodeOffset":"70.47 -5","parent":[0,1]},
{"index":3,"nodeOffset":"67.5 15","parent":[0,1,2]},
{"index":4,"nodeOffset":"53.81 35","parent":[0,1,2,3]},
{"index":5,"nodeOffset":"30.83 49.64","parent":[0,1,2,3,4]},
{"index":6,"nodeOffset":"2.5 55","parent":[0,1,2,3,4]},
{"index":7,"nodeOffset":"-25.83 49.64","parent":[0,1,2,3,4,6]},
{"index":8,"nodeOffset":"-48.81 35","parent":[0,1,2,3,4,6,7]},
{"index":9,"nodeOffset":"-62.5 15","parent":[0,1,2,3,4,6,7,8]},
{"index":10,"nodeOffset":"-65.47 -5","parent":[0,1,2,3,4,6,7,8,9]},
{"index":11,"nodeOffset":"-59.17 -19.64","parent":[0,1,2,3,4,6,7,8,9,10]}
],
"config":{
"algorithm":"Find edge cut Stoer-Wagner"
}}
En la tabla anterior vimos que los tiempos de ejecución de los algoritmos de Karger y de Karger-Stein son iguales, pues Karger-Stein consigue una mejora sobre Karger cuando el número de nodos es grande. Por ejemplo, el grafo de la Figura es también otro completo K25 donde hemos eliminado las aristas del nodo 12 hacia nodos superiores.
Como vemos en los resultados siguientes, Karger se ejecuta en 297 ms cuando Karger-Stein se ejecuta en 188 ms. Y cuanto más nodos y aristas tenga el grafo más eficiente es el segundo respecto al primero. Si lo ejecutamos con Stoer-Wagner sólo necesitamos 4 ms.
30000 iteraciones máximas, opción 1/n
Time: 297 ms
Encontrar corte aristas Karger: {
"edges":[[0,12],[4,12],[9,12],[8,12],[3,12],[6,12],[7,12],[11,12],[1,12],[2,12],[5,12],[10,12]],
"length":12,"repetitions":966,"successProbability":0.96,"contractions":22218,"warnings":[]}
------------------------
30000 iteraciones máximas
Time: 188 ms
Encontrar corte aristas Karger-Stein: {
"edges":[[0,12],[4,12],[2,12],[9,12],[7,12],[8,12],[11,12],[1,12],[10,12],[5,12],[6,12],[3,12]],
"length":12,"repetitions":11,"successProbability":0.96,"contractions":17468,"recursions":5621,"warnings":[]}
------------------------
10000 iteraciones máximas
Time: 4 ms
Find edge cut Stoer-Wagner: {"edges":[[12,0],[12,1],[12,2],[12,3],[12,4],[12,5],[12,6],[12,7],[12,8],[12,9],[12,10],[12,11]],
"weight":12,"a":1,"components":[[12],[0,1,2,3,4,5,6,7,8,9,10,11,13,14,15,16,17,18,19,20,21,22,23,24]],"trace":[]}
{"nodes":[
{"index":0,"nodeOffset":"2.5","parent":-1},
{"index":1,"nodeOffset":"58.45 -23.74","parent":0},
{"index":2,"nodeOffset":"63.77 -20.05","parent":[0,1]},
{"index":3,"nodeOffset":"67.88 -14.16","parent":[0,1,2]},
{"index":4,"nodeOffset":"70.27 -6.43","parent":[0,1,2,3]},
{"index":5,"nodeOffset":"70.54 2.64","parent":[0,1,2,3,4]},
{"index":6,"nodeOffset":"68.42 12.49","parent":[0,1,2,3,4,5]},
{"index":7,"nodeOffset":"63.79 22.5","parent":[0,1,2,3,4,5,6]},
{"index":8,"nodeOffset":"56.69 32.03","parent":[0,1,2,3,4,5,6,7]},
{"index":9,"nodeOffset":"47.32 40.5","parent":[0,1,2,3,4,5,6,7,8]},
{"index":10,"nodeOffset":"36.01 47.36","parent":[0,1,2,3,4,5,6,7,8,9]},
{"index":11,"nodeOffset":"23.22 52.19","parent":[0,1,2,3,4,5,6,7,8,9,10]},
{"index":12,"nodeOffset":"9.51 54.68","parent":[0,1,2,3,4,5,6,7,8,9,10,11]},
{"index":13,"nodeOffset":"-4.51 54.68","parent":[0,1,2,3,4,5,6,7,8,9,10,11]},
{"index":14,"nodeOffset":"-18.22 52.19","parent":[0,1,2,3,4,5,6,7,8,9,10,11,13]},
{"index":15,"nodeOffset":"-31.01 47.36","parent":[0,1,2,3,4,5,6,7,8,9,10,11,13,14]},
{"index":16,"nodeOffset":"-42.32 40.5","parent":[0,1,2,3,4,5,6,7,8,9,10,11,13,14,15]},
{"index":17,"nodeOffset":"-51.69 32.03","parent":[0,1,2,3,4,5,6,7,8,9,10,11,13,14,15,16]},
{"index":18,"nodeOffset":"-58.79 22.5","parent":[0,1,2,3,4,5,6,7,8,9,10,11,13,14,15,16,17]},
{"index":19,"nodeOffset":"-63.42 12.49","parent":[0,1,2,3,4,5,6,7,8,9,10,11,13,14,15,16,17,18]},
{"index":20,"nodeOffset":"-65.54 2.64","parent":[0,1,2,3,4,5,6,7,8,9,10,11,13,14,15,16,17,18,19]},
{"index":21,"nodeOffset":"-65.27 -6.43","parent":[0,1,2,3,4,5,6,7,8,9,10,11,13,14,15,16,17,18,19,20]},
{"index":22,"nodeOffset":"-62.88 -14.16","parent":[0,1,2,3,4,5,6,7,8,9,10,11,13,14,15,16,17,18,19,20,21]},
{"index":23,"nodeOffset":"-58.77 -20.05","parent":[0,1,2,3,4,5,6,7,8,9,10,11,13,14,15,16,17,18,19,20,21,22]},
{"index":24,"nodeOffset":"-53.45 -23.74","parent":[0,1,2,3,4,5,6,7,8,9,10,11,13,14,15,16,17,18,19,20,21,22,23]}
],
"config":{
"nodeValueAuto":"none",
"nodeRadius":2,
"lineColor":"gray",
"algorithm":"Find edge cut Stoer-Wagner",
"maxIter":30000
}}
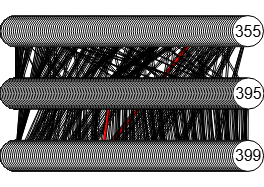
Con el grafo de la Figura con 400 nodos, donde todos los cortes mínimos son de 3 aristas, el algoritmo Stoer-Wagner encuentra un corte mínimo con un máximo de 90000 iteraciones en casi unos 20 segundos. Ya vimos en el tema del corte aristas usando findEdgeCut() y findSTEdgeCut() que resolver ese mismo grafo era impracticable.
Decíamos que en ese grafo todos los cortes mínimos son de 3 aristas, observando en este ejemplo y otros anteriores donde hay más de un corte mínimo que Stoer-Wagner siempre devuelve el último corte mínimo. A continuación se muestra el resultado obtenido donde omitimos con puntos suspensivos el resto de vértices del segundo componente. Vea que el corte separa el último vértice 399 del resto.
Time: 19920 ms
Encontrar corte aristas Stoer-Wagner: {
"edges":[[399,391],[399,392],[399,395]],
"weight":3,
"a":1,
"components":[[399],[0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,
25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,
...
377,378,379,380,381,382,383,384,385,386,387,388,389,390,391,392,393,394,395,396,397,398]],
"trace":[]}Puede abrir cfi-400-nodes.txt con la lista de aristas de ese grafo en formato de texto que puede copiar e importar en la aplicación tal como explicamos en un tema anterior sobre como importar una lista de aristas.
Los otros algoritmos tampoco lo resuelven en un tiempo razonable. El más eficiente Karger-Stein de los implementados lo resuelve con 50000000 iteraciones invirtiendo 173 segundos, un tiempo nada razonable. Observe en la Figura que Karger-Stein encuentra otro de los cortes mínimos con 3 aristas [[214,218], [213,218], [211,218]] que supone separar el vértice 218 del resto. Como Karger-Stein es un algoritmo probabilista, el corte mínimo que encuentre en cada ejecución puede ser diferente en estos casos cuando hay más de un corte mínimo.
Time: 173493 ms
Encontrar corte aristas Karger-Stein: {
"edges":[[214,218],[213,218],[211,218]],
"length":3,
"repetitions":36,
"successProbability":0.9975,
"contractions":15503040,
"recursions":4718556,
"warnings":[]}Todos los algoritmos que se implementan en la aplicación usan la matriz de adyacencia como estructura de datos del grafo. Y no siempre es la óptima. Por ejemplo, para ese grafo con 400 nodos la matriz tiene 400 × 400 = 160000 posiciones. Sin embargo el grafo tiene sólo 600 aristas. Así las diversas operaciones que se llevan a cabo podrían ser más eficientes ejecutarlas sobre la lista de aristas y no sobre la matriz de adyacencia. Pero como he dicho otras veces, mi primer intento es implementar estos algoritmos para ver cómo funcionan, pues es necesario entenderlos antes de hacerlos más eficientes.