Un sitio personal para aprender desarrollo web
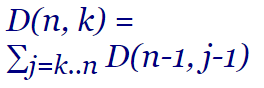
En este tema implementaremos un algoritmo para generar los desarreglos parciales usando la recurrencia D(n, k) = ∑j=k..n D(n-1, j-1) que calcula su valor numérico, tal como vimos en el tema anterior.
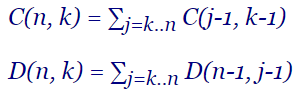
En temas anteriores hemos visto que el valor numérico de los desarreglos parciales se puede calcular con D(n, k) = C(n, k) × D(n-k) y también con D(n, k) = n/k D(n-1, k-1). En este tema buscaremos una tercera forma con similitud con la que ya habíamos visto para las combinaciones C(n, k) = ∑j=k..n C(j-1, k-1), como se observa en la imagen, aplicando D(n, k) = ∑j=k..n D(n-1, j-1)
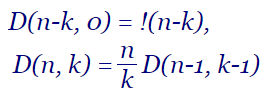
En el tema anterior vimos que la recurrencia D(n, k) = n/k D(n-1, k-1), como se observa en la imagen, también nos sirve para calcular el valor numérico de los desarreglos parciales. En este tema implementaremos un segundo algoritmo para generar los desarreglos parciales basándonos en esa recurrencia.
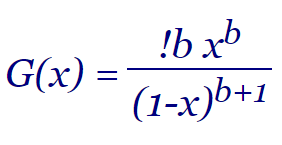
En el tema anterior vimos que el número de desarreglos parciales se calcula con la fórmula D(n, k) = C(n, k) × D(n-k, 0) donde D(n-k, 0) = !(n-k). En este tema vamos a deducir la fórmula recurrente D(n, k) = n/k D(n-1, k-1) para calcular también el valor numérico de los desarreglos parciales, pudiendo expresarse también con la función generadora G(x) = !b xb / (1-x)b+1.
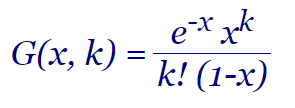
Los desarreglos parciales de una lista con n elementos distintos son todas las sublistas ordenadas con n elementos distintos que se pueden generar de tal forma que solo k elementos aparecen en su posición original. También se pueden definir como las permutaciones de n elementos con k puntos fijos. Las denotamos como D(n, k), correspondiendo con k=0 a los desarreglos sin puntos fijos que vimos en un tema anterior.
También se les denomina Rencontres numbers traducido como Problema de encuentros (o reencuentros). La función generadora de esta familia de funciones combinatorias es G(x, k) = e-x xk / (k! (1-x)). En este tema implementaremos un primer algoritmo para generar los desarreglos parciales.
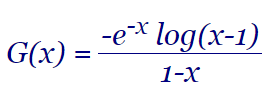
En un apartado del tema anterior que trataba sobre el coste de un algoritmo recursivo para generar desarreglos, habíamos llegado a una función sobre la que omitíamos obtener el término general en ese momento, pues contenía un logaritmo.
Era el producto de e-x/(1-x) que genera los subfactoriales y del logaritmo log(x-1), función que hasta ahora no habíamos tratado de obtener su serie asociada y término general. En este tema analizaremos esto.
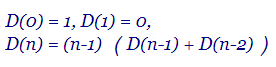
En este tema vamos a implementar un segundo algoritmo para generar los desarreglos de una lista con n elementos. Se basa en la primera recurrencia D(n) = (n-1) ( D(n-1) + D(n-2) ) que expusimos en un tema anterior.
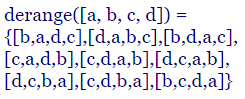
Los desarreglos (derangement) de una lista con n elementos distintos son todas las sublistas ordenadas con n elementos distintos que se pueden generar de tal forma que ninguno aparece en su posición original. Se denota como D(n). Y también como !n, el subfactorial de n.
Una permutación de n elementos tiene uno o más elementos que son puntos fijos si esos elementos se mantienen en su posición original. Desde esta definición un desarreglo es una permutación que no tiene ningún punto fijo.
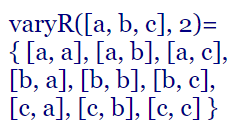
Las variaciones con repetición de una lista con n elementos distintos son todas las sublistas ordenadas con k elementos no necesariamente distintos que se pueden extraer. Su valor es VR(n, k) = nk. En este tema veremos un algoritmo para obtener las permutaciones con repetición.
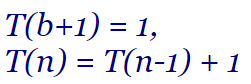
El caso base de una recurrencia condiciona la búsqueda de su solución. Lo más fácil es que sea un caso base particularizado en n=0 o algún valor superior de n. En el primer ejemplo de recurrencias que vimos en esta serie de temas, la del coste del algoritmo que calculaba el factorial cuya recurrencia era T(0) = 1, T(n) = T(n-1) + 1, tenía el caso base en n=0. En este tema veremos algunos ejemplos con un caso base genérico n=b+1, con lo que tendríamos una recurrencia como T(b+1) = 1, T(n) = T(n-1) + 1. Y veremos otra con T(b+1) = 0, T(n) = T(n-1) + n - b - 1. Aunque b es constante con respecto al desarrollo de la recurrencia, la solución del término general será T(n, b) dependiente también de b.
Resolver recurrencias con caso base genérico puede ser fácil usando la técnica del despliegue de la recurrencia. Pero puede complicarse usando la técnica de la función generadora, como sucedió en el tema anterior. Para ello veremos técnicas de actuación sobre el primer caso base y la de secuencia de primeros casos base que pueden ayudar a resolverlas de otra forma. En el tema anterior aplicamos esa última para resolver la recurrencia de las variaciones. En este tema usaremos esas utilidades para resolver partes del desarrollo de esa recurrencia con función generadora.
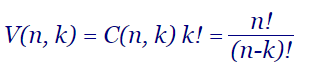
Las variaciones sin repetición de una lista con n elementos distintos son todas las sublistas ordenadas con k elementos distintos que se pueden extraer. Se denota como V(n, k). En este tema veremos varios algoritmos para generar las variaciones.
Al final del tema recopilamos la relación que hay entre las variaciones con los temas anteriores para generar permutaciones, K-tuplas y convolución exponencial de factoriales y potencias.
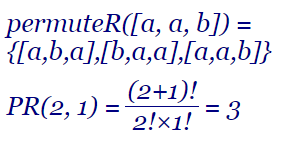
El algoritmo de Heap es un algoritmo de intercambio que supone la forma más eficiente de construir las permutaciones sin repetición. Ese mismo algoritmo lo usamos en el tema anterior para construir las permutaciones con repetición o multinomiales. Pero el coste parece excesivo. Por ejemplo, para el conjunto de partida A = { a, a, a, a, a, a, a } con 7 letras "a" repetidas, el coste es de 57638 iteraciones. Son muchas iteraciones en tanto que las permutaciones con repetición de A es una, el propio A. En este tema buscamos una forma de reducir este coste.
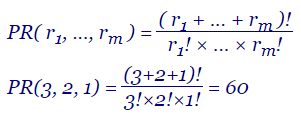
Las permutaciones con repetición, también denominado multinomial, de un conjunto de una lista A = { a1, ..., an } donde pueden producirse repeticiones y al quitar los elementos repetidos obtenemos otra lista { b1, ..., bm } con m≤n elementos distintos, donde cada elemento bi puede estar repetido ri veces, con 0 ≤ ri ≤ n, de tal forma que r1+...+rm = n, son todas las posibles ordenaciones de la lista A. Se denota como PR(r1, ..., rm). En este tema veremos varios algoritmos para generar permutaciones con repetición, uno de ellos usando el algoritmo de Heap que ya vimos en el tema de las permutaciones.
Finalizaremos el tema hablando de los coeficientes multinomiales y la pirámide de Pascal, concepto que amplía el de coeficientes binomiales con dos variables (x+y)n a más variables, como por ejemplo (x+y+z)n con 3 variables.

Exportar un trozo de HTML a una imagen se basa en la facultad de albergar un SVG (Scalable Vector Graphics) en un elemento imagen (IMG). Se usa la API Image(), que es un constructor del elemento imagen, conjuntamente con un Canvas para convertir el SVG en un formato de imagen, como PNG, JPG y otros. Un SVG no es otra cosa que un XML. Y yo empecé a estudiar HTML aprendido primero XHTML que debe ser escrito como XML. Es necesario respetar las reglas XHTML en el trozo de HTML que queremos convertir en imagen, pero no es nada complicado. La imagen adjunta es un archivo PNG que se extrae de un trozo de HTML, como veremos en un ejemplo interactivo en ese tama.
En este tema intentaré explicar cómo se hace, pues de paso recordaremos cosas que se relacionan como SVG, XML, XHTML, HTML-5, Base64, Canvas e Image. Y otras cosas relacionadas con la serialización de bytes, manejando Base64 con el uso de los métodos encodeURIComponent(), btoa() y atob(). O bien con TextEncoder y TextDecoder, donde se usa el array tipado (Typed Array) Uint8Array, que junto a Blob y objetos URL veremos también para la descarga de archivos, algo que explicaremos en el último apartado.

En este tema veremos las clases del módulo Math que nos permiten escribir HTML y CSS suficiente para presentar visualmente una fórmula matemática. Y, adicionalmente, poder extraerla como una expresión en lenguaje natural válida para usarla en aplicaciones como Wolfram Alpha.
En la imagen puede ver como presentamos la raíz cuadrada usando el símbolo UNICODE "√". El estilo en forma de clases con un guion bajo inicial y dos letras aplicarán lo necesario para incluir la línea superior que abarca la raíz, algo que el simple caracter "√" no incluye. En lenguaje natural la extraemos como sqrt(n), expresión que podemos usar en Wolfram Alpha y otras aplicaciones. Empecemos por listar las clases disponibles con la versión actual.