Subfactoriales y logaritmos
Función generadora con exponencial y logaritmo
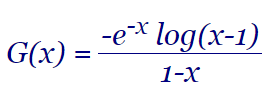
En un apartado del tema anterior que trataba sobre el coste de un algoritmo recursivo para generar desarreglos, habíamos llegado a una función sobre la que omitíamos obtener el término general en ese momento, pues contenía un logaritmo.
Era el producto de e-x/(1-x) que genera los subfactoriales y del logaritmo log(x-1), función que hasta ahora no habíamos tratado de obtener su serie asociada y término general:
| G(x) = | -e-x log(x-1) |
| 1-x |
De forma indirecta en ese tema anterior nos servimos de OEIS para descubrir que esa función generadora exponencial respondía a la secuencia siguiente:
Esa secuencia, que se inicia en n≥1, es la misma que obteníamos de forma indirecta en el tema anterior, aunque allí le agregábamos el término A(0) = 0. En OEIS también exponen este término general:
También en el tema anterior vimos otra fórmula equivalente, que fue la que usamos para la solución final de la recurrencia del coste del algoritmo que generaba los desarreglos, conteniendo H(n-j) que es el número armónico:
| A(n) = ∑j=0..n-1 | (-1) j n! | H(n-j) |
| j! |
En OEIS usa log(1-x) en lugar de log(x-1), luego volveremos sobre esto, con este desarrollo de Taylor:
| -e-x | log(1-x) | = | 1 x1 | + | 1 x2 | + | 5 x3 | + | 20 x4 | + | 109 x5 | + | 689 x6 | + | 5053 x7 | +... |
| 1-x | 1! | 2! | 3! | 4! | 5! | 6! | 7! |
Se observa que los numeradores son los mismos que los de la secuencia dada. Sin embargo si tratamos de obtener esto en Wolfram Alpha no lo vamos a encontrar. Cuando hacemos equivaler una función con una serie se suele condicionar a algo como |x|<1, de tal forma que x es un número real. Pero en la función tenemos log(x-1) con lo que para |x|<1 tendremos números negativos, para los que el logaritmo no está definido entre los reales, aunque si en los complejos. Podemos hacer esto:
Así (x-1)2 siempre tomará valores positivos para |x|<1. Y además (x-1)2 = (1-x)2. Entonces nuestra función queda así, cuyo desarrollo de Taylor podemos ver en WolframAlpha que ahora si produce la secuencia dada:
| -e-x | log(x-1) | = -e-x | log((1-x)2) | = | 1 x1 | + | 1 x2 | + | 5 x3 | + | 20 x4 | + | 109 x5 | + O(x6) |
| 1-x | 2 (1-x) | 1 | 2 | 6 | 24 | 120 |
En cualquier caso podemos obtener el desarrollo de Taylor de -e-x log(x-1) / (1-x) directamente, como se muestra en el siguiente desplegable.
Así que teniendo el término general y el desarrollo de Taylor podemos expresarlo como una función generadora exponencial usando cualquiera de los dos términos generales de A(n) que vimos en [1] o [2]:
| -e-x | log(x-1) | = ∑n≥0 ( ∑k=1..n (-1)n-k C(n, k) k! H(k) ) | xn | = |
| 1-x | n! |
| = ∑n≥0 ( ∑j=0..n-1 | (-1) j n! | H(n-j) ) | xn |
| j! | n! |
Verificando la corrección de los términos generales
El asunto ahora es verificar matemáticamente que eso es cierto, pues de serlo estamos seguros que podemos usar A(n) en nuestra solución de la recurrencia del tema anterior. En primer lugar veamos que relación hay entre log(x-1) y log(1-x), pues como vimos más arriba, OEIS usaba esta segunda forma.
En el desplegable anterior vimos porque log(-1) = i π. Y además que podíamos despreciar la parte compleja pues lo que estamos buscando son las partes reales. Así que a nuestros efectos es equivalente usar log(1-x) en nuestra función puesto que ignoraremos la parte compleja:
| G(x) = -e-x | log(x-1) | = -e-x | (log(1-x) + i π) | = - | e-x log(1-x) | - i | π e-x |
| 1-x | 1-x | 1-x | 1-x |
Observe que la parte imaginaria tiene la función e-x / (1-x) que es la función generadora del subfactorial, cuya secuencia es !n = 1, 0, 1, 2, 9, 44, 265, 1854, ... como vimos en el desplegable anterior. Vamos a buscar la serie con su término general de la parte real:
| G(x) = | e-x | × (- log(1-x)) |
| 1-x |
Intencionadamente hemos separado esto en dos partes, por un lado la primera que es el subfactorial que vimos en el tema de los desarreglos:
| G1(x) = | e-x | = ∑n≥0 !n | xn |
| 1-x | n! |
Y la segunda que contiene el logaritmo:
Intentemos encontrar la serie asociada a este logaritmo usando Taylor:
| f(x) = ∑n≥0 | f n(0) | xn |
| n! |
Empecemos
| f 1(x) = | d | (- log(1-x)) | = | 1 | ⇒ f 0(0) = 1 |
| dx | 1-x |
| f 2(x) = | 1 | ⇒ f 1(0) = 1 |
| (1-x)2 |
| f 3(x) = | 2 | ⇒ f 2(0) = 2 |
| (1-x)3 |
| f 4(x) = | 6 | ⇒ f 3(0) = 6 |
| (1-x)4 |
| f 5(x) = | 24 | ⇒ f 4(0) = 24 |
| (1-x)5 |
| f 6(x) = | 120 | ⇒ f 4(0) = 120 |
| (1-x)6 |
Entonces
| f(x) = ∑n≥0 | f n(0) | xn | = | 0 | x0 + | 1 | x1 + | 1 | x2 + | 2 | x3 + | 6 | x4 + | 24 | x5 + ... = |
| n! | 0! | 1! | 2! | 3! | 4! | 5! |
| = | 0! | x1 + | 1! | x2 + | 2! | x3 + | 3! | x4 + | 4! | x5 + ... = |
| 1! | 2! | 3! | 4! | 5! |
| = | x | + | x2 | + | x3 | + | x4 | + | x5 | = |
| 1 | 2 | 3 | 4 | 5 |
| =∑n≥1 | 1 | xn | = ∑n≥1 | n! | xn | = ∑n≥1 (n-1)! | xn |
| n | n | n! | n! |
El número armónico
Entonces la segunda función con el logaritmo da lugar a una serie armónica:
| G2(x) = -log(1-x) = ∑n≥1 (n-1)! | xn | = ∑n≥1 | 1 | xn |
| n! | n |
Como para n=0 lo anterior no estaría definido, vamos a reformularlo pues necesitamos el producto de dos series que se inician en cero (ver en WolframAlpha):
| = ∑n≥0 ( | ⎧ | ⎰ | 1/n | n≥1 | ⎫ | xn ) |
| ⎩ | ⎱ | 0 | n=0 | ⎭ |
El n-ésimo número armónico se define como la suma de los recíprocos de los primeros n números naturales, con esta serie para n≥1:
Genera la secuencia con términos fraccionarios siguiente:
Si ajustamos la fracción para que se corresponda con un denominador con n! tendremos la secuencia
También puede obtenerse de forma recurrente:
| H(n) = H(n-1) + | 1 |
| n |
Otra alternativa es usando los números de Stirling de primera clase, que exponemos en el siguiente apartado:
| H(n) = | S(n+1, 2) |
| n! |
Los valores sin signo para n≥1 son los siguientes:
Por lo tanto los primeros valores de los números armónicos son los que resultan dividiendo Stirling por subfactorial, partiendo de n≥1:
| H(n) = | S(n+1, 2) | = 1/1!, 3/2!, 11/3!, 50/4!, 274/5!, 1764/6!, ... |
| n! |
Números de Stirling de primera clase
S(n, k) o bien [nk] son los números de Stirling de primera clase sin signo pueden definirse como el número permutaciones de n elementos en k ciclos disjuntos, contando las permutaciones cíclicas que veremos en un tema posterior. Obedecen a la siguiente recurrencia:
n=0 ∨ k=0 ∨ n<k ⇒ S(n, k) = 0,
S(n, k) = (n-1) S(n-1, k) + S(n-1, k-1)
Los primeros valores pueden obtenerse en la aplicación Combine Tools, en la pestaña "Numéricos":
| n↓k→ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0 | 2 | 3 | 1 | 0 | 0 | 0 | 0 |
| 4 | 0 | 6 | 11 | 6 | 1 | 0 | 0 | 0 |
| 5 | 0 | 24 | 50 | 35 | 10 | 1 | 0 | 0 |
| 6 | 0 | 120 | 274 | 225 | 85 | 15 | 1 | 0 |
| 7 | 0 | 720 | 1764 | 1624 | 735 | 175 | 21 | 1 |
No debemos confundirlos con los que tienen signo que obedece a la recurrencia
n=0 ∨ k=0 ∨ n<k ⇒ s(n, k) = 0,
s(n, k) = - (n-1) s(n-1, k) + s(n-1, k-1)
con estos valores numéricos
| n↓k→ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | -1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0 | 2 | -3 | 1 | 0 | 0 | 0 | 0 |
| 4 | 0 | -6 | 11 | -6 | 1 | 0 | 0 | 0 |
| 5 | 0 | 24 | -50 | 35 | -10 | 1 | 0 | 0 |
| 6 | 0 | -120 | 274 | -225 | 85 | -15 | 1 | 0 |
| 7 | 0 | 720 | -1764 | 1624 | -735 | 175 | -21 | 1 |
Ambas se equiparan así:
Los números de Stirling de primera clase son los coeficientes s(n, k) (con signo) del factorial descendente (o falling factorial):
Por ejemplo:
siendo los coeficientes s(3, 3) = 1, s(3, 2) = -3, s(3, 1) = 2 tal como se observa en la tabla de valores anterior.
Por otro lado, los números de Stirling sin signo S(n, k) se corresponden con los coeficientes del factorial ascendente (o símbolo de Pochhammer):
El producto de Cauchy o convolución de exponenciales y logaritmos
Antes en [3] habíamos presentado este producto de funciones exponencial y logarítmica:
| G(x) = | e-x | × (- log(1-x)) |
| 1-x |
Como ya conocemos las series asociadas a ambas funciones, vamos a realizar ese producto o convolución de funciones, pero antes recordamos el producto de Cauchy:
Lo anterior es cierto si p0 = 0, pues vamos a tomar pn como el término de la serie armónica [7] que proviene del logaritmo. Y además la suma ∑k=1..0 es cero al tener un rango invertido.
Así que tomando pn como el término de la serie [7] y qn como el término de la serie [4], entonces el producto [3] queda así:
| G(x) = G1(x) × G2(x) = ( ∑n≥0 | !n | xn | ) × ( ∑n≥0 | 1 | xn | ) = |
| n! | n |
| = ∑n≥1 | ( ∑k=1..n | !(n-k) | × | 1 | ) xn |
| (n-k)! | k |
Veamos el término de la serie, al que denominaremos B(n), usando la definición del subfactorial que era !n = ∑j=0..n (-1) j n! / j!
| B(n) = ∑k=1..n | !(n-k) | × | 1 | = |
| (n-k)! | k |
| = ∑k=1..n ( ∑j=0..n-k | (-1) j (n-k)! | ) × | 1 | = |
| j! (n-k)! | k |
| = ∑k=1..n ( ∑j=0..n-k | (-1) j | ) × | 1 |
| j! | k |
Al incluir este término en la función generadora [8] nos quedará:
| G(x) = ∑n≥1 B(n) xn | = ∑n≥1 B(n) n! | xn | = ∑n≥0 A(n) | xn |
| n! | n! |
Hemos definido A(n) = B(n) n! Observe que podemos reajustar el rango a n≥0 pues hemos redefinido el caso n=0 en [7] donde forzamos p0 = 0 al desarrollar el producto de Cauchy. Se observa que podemos modificar el rango del sumatorio exterior, pues llegamos a un sumatorio con rango invertido cuya suma es cero:
Entonces A(n) pueden ser las dos ya vistas en [1] y [2] (cuya equivalencia ya demostramos en un apartado del tema anterior) a su vez supuestamente equivalentes también con esta última que acabamos de obtener:
| = ∑j=0..n-1 | (-1) j n! | H(n-j) = |
| j! |
| = ∑k=1..n ( ∑j=0..n-k n! | (-1) j | ) × | 1 |
| j! | k |
Para asegurarnos de que la tercera es equivalente a las otras dos, calcularemos los primeros valores, desde n = 1 hasta n = 8
Hemos resuelto lo anterior con ayuda, como por ejemplo para el último caso, en WolframAlpha. Vemos que esta secuencia A(n) = 1, 1, 5, 20, 109, 689, 5053, 42048, ... es precisamente la que obteníamos con las dos primera fórmulas equivalentes. Veamos si podemos demostrar que esto es cierto. Para ello tomemos esta expresión genérica:
Si aj = (-1) j n! / j! y, por otro lado, bk = 1/k entonces si:
| = ∑k=1..n ( ∑j=0..n-k n! | (-1) j | ) × | 1 |
| j! | k |
sucederá que es equivalente a esta
| = ∑j=0..n-1 | (-1) j n! | ( ∑k=1..n-j | 1 | ) = |
| j! | k |
| = ∑j=0..n-1 | (-1) j n! | H(n-j) |
| j! |
Hemos identificado H(n-j) como vemos en WolframAlpha, como el (n-j)-ésimo número armónico, pues el n-ésimo número armónico es H(n) = ∑k=1..n 1/k, con lo que demostramos la equivalencia de la tercera con la segunda fórmula en [10] y, a su vez, con la primera pues ya se demostró la equivalencia de las dos primeras.