Caso base genérico en una recurrencia
Caso base genérico para la recurrencia del factorial
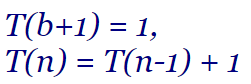
El caso base de una recurrencia condiciona la búsqueda de su solución. Lo más fácil es que sea un caso base particularizado en n=0 o algún valor superior de n. En el primer ejemplo de recurrencias que vimos en esta serie de temas, la del coste del algoritmo que calculaba el factorial cuya recurrencia era T(0) = 1, T(n) = T(n-1) + 1, tenía el caso base en n=0 con este algoritmo:
function factorial(n){
if (n===0){
return 1;
} else {
return n*factorial(n-1);
}
}| T(n) = { | 1 | si n=0 |
| T(n-1) + 1 | si n>0 |
Para esta recurrencia que podemos expresar como T(0) = 1, T(n) = T(n-1) + 1 encontramos la función generadora, serie y solución siguiente:
| G(x) = | 1 | = ∑n≥0 (n+1) xn |
| (1-x)2 |
Si es un caso base genérico en n = b+1 con -1 ≤ b ≤ n-1, tendríamos esta definición:
| T(n) = { | 1 | si n=b+1 |
| T(n-1) + 1 | si n>b+1 |
O bien expresada T(b+1) = 1, T(n) = T(n-1) + 1 tiene por solución la siguiente tal como se observa en WolframAlpha:
Aunque b es constante con respecto al desarrollo de la recurrencia, la solución del término general debería ponerse como T(n, b) = n - b, pues es dependiente también del valor de b.
Apliquemos la técnica de la función generadora para llegar a esa solución. Sea la función generadora en serie de potencias, recordando lo que vimos en el tema sobre desplazamiento del caso base:
que aplicaremos a la recurrencia desplazando el índice para evitar negativos:
Quedando:
Trabajamos sobre el término de la izquierda en [3], observando que la condición inicial es:
Entonces
| = | 1 | ∑n≥b+1 T(n+1) xn+1 | = | 1 | ∑n≥b+2 T(n) xn | = |
| x | x |
| = | 1 | ( - T(b+1) xb+1 + ∑n≥b+1 T(n) xn ) = |
| x |
| = | 1 | ( - Gb+1(x) + G(x) ) = |
| x |
| = - xb + | G(x) |
| x |
Se observa donde interviene la condición inicial. Por otro lado tenemos el término de la derecha en [3]:
| = | xb+1-1 | + | 1 | = | xb+1 |
| 1-x | 1-x | 1-x |
Vease que esto no es otra cosa que la aplicación de la serie geométrica, donde se observa la suma parcial de la serie:
| ∑n=0..b xn = | 1-xb+1 |
| 1-x |
Entonces [3] nos queda así:
| -xb + | G(x) | = G(x) + | xb+1 |
| x | 1-x |
Despejando G(x)
| G(x) = | xb+1 |
| (1-x)2 |
Buscar una serie para esta expresión no es tan obvio como aparenta, pues si lo resolvemos en Wolfram Alpha obtenemos series que nada se parecen con la inicial que hemos utilizado en [2] (aunque suponemos son equivalentes).
La primera idea es usar el Desarrollo de Taylor, pero tanto la función como las primeras b+1 derivadas resultarán cero si particularizamos en x=0. Aunque podríamos usar un atajo para resolverlo (ver un apartado más abajo), a continuación mostraremos el uso de otros medios para resolverlo.
Resolver actuando sobre el primer caso base
La primera alternativa es ver que ya tenemos demostrada la solución vista en [1] para la recurrencia T(0)=1, T(n)=T(n-1)+1:
| G(x) = | 1 | = ∑n≥0 (n+1) xn |
| (1-x)2 |
Entonces haremos lo siguiente:
| 1 | = ∑n≥0 (n+1) xn | = | xb+1 | ∑n≥0 (n+1) xn | = |
| (1-x)2 | xb+1 |
| = | 1 | ∑n≥0 (n+1) xn xb+1 | = | 1 | ∑n≥0 (n+1) xn+b+1 | = |
| xb+1 | xb+1 |
| = | 1 | ∑n≥b+1 (n-b) xn |
| xb+1 |
En lo anterior ajustamos índice inicial del rango para llegar a una suma que se inicia en n=b+1, de donde se deduce
| xb+1 | = ∑n≥b+1 (n-b) xn |
| (1-x)2 |
Por lo que la solución general a la recurrencia T(b+1)=1, T(n)=T(n-1)+1 partiendo de la función generadora usada G(x) = ∑n≥b+1 T(n) xn es:
Para b = - 1 con caso base T(b+1) = 1 ⇒ T(0) = 1 tenemos la solución esperada T(n) = n + 1.
Resolver usando una secuencia de primeros casos base
La segunda alternativa se deduce a partir de b = -1, 0, 1, 2, 3,..., tratando de obtener una solución general a partir de esta secuencia. Esto fue lo que usamos en el tema anterior sobre las variaciones.
Veamos para nuestra recurrencia T(b+1)=1, T(n)=T(n-1)+1, donde no es díficil resolver cada recurrencia tal y como hicimos antes para b=-1 ⇒ T(0) = 1. O bien usar Wolfram Alpha para resolverla:
Siguiendo la secuencia hacemos suposiciones para valores iguales o mayores que b. Con el valor b, que produce la recurrencia objeto de este apartado, podemos suponer que el término general es:
Aplicando inducción, si es cierto para b=-1 y la hipótesis de inducción es:
debemos obtener el término general T(n) = n - (b+1) para b+1, con lo que partimos de la función generadora
Hemos llegado al término general esperado, por lo que se demuestra la corrección de la solución T(n) = n-b.
En la serie de recurrencias que resolvimos antes con WolframAlpha hemos supuesto lo siguiente para el caso b+c, de tal forma que cuando c=0 estamos en la recurrencia de este apartado que tiene el caso base en b+1 y tenemos la expresión [5]:
| xb+c+1 | =∑n≥b+c+1 (n-b-c) xn |
| (1-x)2 |
Esto nos va a servir para cuando tengamos una función generadora cuyo numerador sea de la forma xb+c+1 siendo b un valor indeterminado y c un valor concreto.
Otra recurrencia con caso base genérico
Veamos ahora esta otra recurrencia:
| T(n) = { | 0 | si n=b+1 |
| T(n-1) + n - b - 1 | si n>b+1 |
Esta recurrencia se puede expresar como T(b+1) = 0, T(n) = T(n-1) + n - b - 1 y tiene por solución general tal como se observa en WolframAlpha
Si aplicamos valores desde b=0 a la recurrencia y las resolvemos con WolframAlpha (o resolverlas directamente pues no es díficil) se observa que se puede deducir esa solución:
Si aplicamos la función generadora G(x) = ∑n≥b+1 T(n) xn en serie de potencias para llegar a esa solución obtenemos la siguiente función, lo que puede comprobar en el desplegable:
| G(x) = | xb+2 |
| (1-x)3 |
Por lo tanto la solución debe ser
| xb+2 | = ∑n≥b+1 1/2 (n-b)(n-b-1) xn |
| (1-x)3 |
De esta función no se deduce directamente la solución general anterior en WolframAlpha, por lo que lo deduciremos de los primeros valores:
Resolviendo las sumas con WolframAlpha vemos que podemos deducir que el término general es el que genera esa función, pudiéndose demostrar por inducción como hicimos en el apartado anterior. O bien usar la misma técnica que en el segundo apartado, partiendo del primer caso particular en el despligue anterior:
de donde se deduce lo que que queremos demostrar:
Como hicimos en el apartado anterior, en la serie de recurrencias que resolvimos antes con WolframAlpha hemos supuesto lo siguiente en la última línea para el caso b+c, de tal forma que cuando c=0 estamos en la recurrencia de este apartado que tiene el caso base en b+1 y tenemos la expresión [7]:
| xb+c+2 | =∑n≥b+c+1 (n-b-c)(n-b-c-1) xn |
| (1-x)3 |
Esto nos va a servir para cuando tengamos una función generadora cuyo numerador sea de la forma xb+c+2 siendo b un valor indeterminado y c un valor concreto.
Resolver aplicando Desarrollo de Taylor en x=0
Con las dos funciones generadoras que vimos en apartados anteriores:
| xb+1 | = ∑n≥b+1 (n-b) xn |
| (1-x)2 |
| xb+2 | = ∑n≥b+1 1/2 (n-b)(n-b-1) xn |
| (1-x)3 |
Para usar el Desarrollo de Taylor, como las derivadas iniciales resultarán cero, haremos esto. Empezando por la primera:
| G(x) = xb+1 × | 1 | = xb+1 × f(x) |
| (1-x)2 |
Y aplicaremos el Desarrollo de Taylor a f(x) = 1/(1-x)2, algo que ya hemos obtenido en un tema anterior y cuya solución general usaremos a continuación:
| G(x) = xb+1 f(x) = | xb+1 | = xb+1 ∑n≥0 | f n(0) | xn | = xb+1 ∑n≥0 (n+1)! | xn | = |
| (1-x)2 | n! | n! |
Al ajustar el índice del sumatorio vemos que alcanzamos la solución esperada. Haciendo lo mismo para f(x) = 1/(1-x)2 cuyo Desarrollo de Taylor también obtuvimos en un tema anterior:
| G(x) = xb+2 f(x) = | xb+2 | = xb+2 ∑n≥0 | f n(0) | xn | = xb+2 ∑n≥0 (n+1)! ½ (n+2) | xn | = |
| (1-x)3 | n! | n! |
Se observa que podemos hacer el último ajuste en el índice del sumatorio, dado que en la posición b+1 vale cero.
Resolver la recurrencia de las variaciones con caso base genérico
En el tema anterior teníamos la siguiente recurrencia con caso base genérico para resolver el algoritmo que generaba las variaciones:
| T(n) = | { | 1 | n = b + 1 |
| n T(n-1) + n2 + n + 1 + ((n-b)/b!) n! | n > b + 1 |
En ese tema no usamos la técnica de la función generadora para obtener la solución. Utilizamos la técnica de ver los primeros casos particulares y de ahí deducir la solución general, como hicimos en apartados anteriores de este tema. Con ayuda de los apartados anteriores, intentemos ahora aplicar la función generadora a la recurrencia que podemos expresar así:
Incrementamos índices:
Dividimos entre n+1:
Operando algunas cosas queda:
Aplicamos la función generadora exponencial
| G(x) = ∑n≥b+1 T(n) | xn |
| n! |
La condición inicial es
| Gb+1(x) = | xb+1 |
| b+1! |
Aplicando a [9] vamos resolviendo cada término empezando por la izquierda:
- ∑n≥b+1 T(n+1)/(n+1) xn/n! = ∑n≥b+1 T(n+1) xn/(n+1)! == ∑n≥b+1 T(n+1) xn+1 x-1/(n+1)! == 1/x ∑n≥b+1 T(n+1) xn+1/(n+1)! == 1/x ∑n≥b+2 T(n) xn/n! == 1/x (- T(b+1) xb+1/(b+1)! + ∑n≥b+1 T(n) xn/n! ) == 1/x (- xb+1/(b+1)! + G(x) ) == - xb/(b+1)! + 1/x G(x)
Vease que en el penúltimo paso anterior se aplica la condición inicial.
- ∑n≥b+1 T(n) xn/n! = G(x)
- ∑n≥b+1 n xn/n! == - ∑n=0..b n xn/n! + ∑n≥0 n xn/n! == - ∑n=0..b xn/(n-1)! + x ex == - ∑n=0..b xn-1 x1/(n-1)! + x ex == - x ∑n=0..b xn-1/(n-1)! + x ex == - x ∑n=-1..b-1 xn/n! + x ex == - x ( x-1/(-1)! - xb/b! + ∑n=0..b xn/n! ) + x ex == - x ( 0 - xb/b! + ∑n=0..b xn/n! ) + x ex == xb+1/b! - x ∑n=0..b xn/n! + x ex
En lo anterior usamos ∑n≥0 n xn/n! = x ex algo que ya hemos visto en temas anteriores, pero que es fácil deducir de la propia definición de ex = ∑n≥0 xn/n! pues:
x ex = x ∑n≥0 xn/n! = ∑n≥0 xn+1/n! = ∑n≥1 xn/(n+1)! == ∑n≥1 n/n xn/(n+1)! = ∑n≥1 n xn/n! == - 0 x0/0! + ∑n≥0 n xn/n! = ∑n≥0 n xn/n!Y también resolvemos x-1/(-1)! = 0 pues el factorial negativo en el denominador hace que la fracción sea cero, tal como vimos en un tema anterior 1/(-n)!=0.
- ∑n≥b+1 2 xn/n! == - 2 ∑n=0..b xn/n! + 2 ∑n≥0 xn/n! == - 2 ∑n=0..b xn/n! + 2 ex
- ∑n≥b+1 1/(n+1) xn/n! = ∑n≥b+1 xn/(n+1)! == ∑n≥b+1 xn+1 x-1/(n+1)! == 1/x ∑n≥b+1 xn+1/(n+1)! == 1/x ( - ∑n=0..b xn+1/(n+1)! + ∑n≥0 xn+1/(n+1)! ) == 1/x ( - ∑n=0..b xn+1/(n+1)! + ex - 1 ) == 1/x ( - ∑n=1..b+1 xn/n! + ex - 1 ) == 1/x ( - ( -x0/0!+xb+1/(b+1)!+ ∑n=0..b xn/n! ) + ex - 1 ) == 1/x ( - (-1+xb+1/(b+1)!+ ∑n=0..b xn/n! ) + ex - 1 ) == 1/x ( 1 - xb+1/(b+1)! - ∑n=0..b xn/n! + ex - 1 ) == 1/x ( - xb+1/(b+1)! - ∑n=0..b xn/n! + ex ) =
= - xb - 1 ∑n=0..b xn + ex (b+1)! x n! x En la línea quinta hemos aplicado esta resolución:
∑n≥0 xn+1/(n+1)! = ∑n≥1 xn/n! = -x0/0! + ∑n≥0 xn/n! = ex-1 - ∑n≥b+1 1/b! n n! xn/n! = ∑n≥b+1 1/b! n xn == 1/b! (- ∑n=0..b n xn + ∑n≥0 n xn ) == 1/b! (- ∑n=0..b n xn + x/(1-x)2 ) =
= 1 ( - b xb+2 + (b+1) xb+1 - x + x ) = b! (1-x)2 (1-x)2 = - b xb+2 + b+1 xb+1 b! (1-x)2 b! (1-x)2 En la cuarta línea hemos resuelto ∑n=0..b n xn de esta forma:
∑n=0..b n xn = x + 2 x2 + 3 x3 + ... + b xbPor otro lado
x ∑n=0..b n xn = x2 + 2 x3 + 3 x4 + ... + (b-1) xb + b xb+1Restando nos queda
∑n=0..b n xn - x ∑n=0..b n xn = x + x2 + x3 + ... + xb - b xb+1 == ∑n=1..b xn - b xb+1 = - x0 + ∑n=0..b xn - b xb+1 == -1 + (1-xb+1)/(1-x) - b xb+1En lo anterior observamos la suma de la serie geométrica es ∑n=0..b xn = (1-xb+1)/(1-x). Entonces
(1-x) ∑n=0..b n xn = -1 + (1-xb+1)/(1-x) - b xb+1De donde obtenemos lo que estamos buscando:
∑n=0..b n xn = -1/(1-x) + (1-xb+1)/(1-x)2 - b xb+1/(1-x) == b xb+2 - (b+1) xb+1 + x (1-x)2 - ∑n≥b+1 (b-1)/b! n! xn/n! == (b-1)/b! (- ∑n=0..b xn + ∑n≥0 xn ) == (b-1)/b! ( - (1-xb+1)/(1-x) + 1/(1-x) ) =
= b-1 xb+1 b! 1-x Aquí también hemos aplicado la suma que vimos antes ∑n=0..b xn = (1-xb+1)/(1-x)
Una vez resueltos los pasos de A) hasta G) los tenemos que poner en [9].
| - | xb | + | 1 | G(x) = |
| (b+1)! | x |
| + | xb+1 | - x ∑n=0..b | xn | + x ex - |
| b! | n! |
| - 2 ∑n=0..b | xn | + 2 ex - |
| n! |
| - | xb | - | 1 | ∑n=0..b | xn | + | ex | - |
| (b+1)! | x | n! | x |
| - | b | xb+2 | + | b+1 | xb+1 | - |
| b! | (1-x)2 | b! | (1-x)2 |
| - | b-1 | xb+1 |
| b! | 1-x |
Los términos en color rojo se anulan. Por otro lado podemos agrupar los 3 términos que multiplican a ex y también los 3 que multiplican a ∑n=0..b xn/n!
| + | xb+1 | - | b | xb+2 | + | b+1 | xb+1 | - | b-1 | xb+1 |
| b! | b! | (1-x)2 | b! | (1-x)2 | b! | 1-x |
Despejando G(x) tras simplificar queda:
| G(x) = | (1+x)2 | ( ex - ∑n=0..b xn/n! ) | + | (x2 - 3x + 3) xb+2 |
| (1-x) | b! (1-x)3 |
Resolviendo el término exponencial
Veamos el primer sumando en [10]:
Observe la anulación de los sumatorios con rango n=0..b. Más abajo volveremos sobre esto. Ya resolvimos esa expresión final en el tema de las Permutaciones para n≥0:
| (1+x)2 | ∑n≥0 | xn | = | (1+x)2 | ex | = |
| 1-x | n! | 1-x |
| = ∑n≥0 ( 4 ( ∑j=0..n | n! | ) - n - 3 ) | xn |
| j! | n! |
Ajustamos el inicio del sumatorio externo en n≥b+1 y también el del sumatorio interno j=b+1, pues su inicio está condicionado al del sumatorio externo:
| (1+x)2 | (ex-∑n=0..b xn/n!) = ∑n≥b+1 ( 4 ( ∑j=b+1..n | n! | ) - n - 3 ) | xn |
| 1-x | j! | n! |
En el tema de permutaciones hacíamos algunos ajustes de índices de sumatorios apareciendo términos que se anulaban. Por un lado aparecía -1-4x que se anulaba con otro 1+4x al hacer un ajuste en el sumatorio externo. Y por otro aparecía -10 n! que se anulaba con otro 10 n! al hacer un ajuste en el índice del sumatorio interno. Dado que la recurrencia de las permutaciones es una particularización de la de las variaciones que estamos viendo aquí, en el desplegable siguiente podemos ver de donde salen esas anulaciones, con lo que de alguna forma probamos la corrección de [11].
Resolviendo el término en potencias
Veamos el segundo sumando en [10]:
| (x2 - 3x + 3) xb+2 | = | xb+2 | × | (2-x)(1-x) + 1 | = | xb+2 | ( | 2-x | + | 1 | ) = |
| b! (1-x)3 | b! | (1-x)3 | b! | (1-x)2 | (1-x)3 |
| = | 2 xb+2 | - | xb+3 | + | xb+2 |
| b! (1-x)2 | b! (1-x)2 | b! (1-x)3 |
Usaremos [5], expresión que era xb+1/(1-x)2 = ∑n≥b+1 (n-b) xn que vimos en los primeros apartados y cambiando b por b+1 :
| 2 | xb+2 | = | 2 | ∑n≥(b+1)+1 (n-(b+1)) xn | = | 2 | ∑n≥b+2 (n-b-1) xn | = |
| b! | (1-x)2 | b! | b! |
| = | 2 | ( - ∑n=b+1..b+1 (n-b-1) xn + ∑n≥b+1 (n-b-1) xn ) = |
| b! |
| = | 2 | ( - 0 + ∑n≥b+1 (n-b-1) xn ) = |
| b! |
| = | 2 | ∑n≥b+1 (n-b-1) xn |
| b! |
Resolvemos el segundo término también con [5] xb+1/(1-x)2 = ∑n≥b+1 (n-b) xn cambiando b por b+2
| 1 | xb+3 | = | 1 | ∑n≥(b+2)+1 (n-(b+2)) xn | = | 1 | ∑n≥b+3 (n-b-2) xn | = |
| b! | (1-x)2 | b! | b! |
| = | 1 | ( - ∑n=b+1..b+2 (n-b-2) xn + ∑n≥b+1 (n-b-2) xn ) = |
| b! |
| = | 1 | ( - (-1) xb+1 - 0 + ∑n≥b+1 (n-b-2) xn ) = |
| b! |
| = | 1 | ( xb+1 + ∑n≥b+1 (n-b-2) xn ) | = |
| b! |
| = | 1 | ∑n≥b+1 (n-b-2) xn |
| b! |
En lo anterior obtenemos el término xb+1 por fuera del sumatorio, un problema que en principio no sé como resolver. Pues se intenta obtener una serie de sumatorios como ∑n≥b+1 para poder obtener el término general partiendo de la definición que utilizamos para la función generadora. He revisado repetidas veces los cálculos anteriores por si hubiera algo que hiciera desaparecer ese término, pero no he encontrado nada al respecto ¿Podemos ignorar ese término y tomar sólo el sumatorio?
Dejemos un momento este problema que veremos en el siguiente apartado y veamos el último término donde usamos [7] directamente xb+2/(1-x)3 = ∑n≥b+1 1/2 (n-b-1)(n-b) xn sin más transformaciones:
| 1 | xb+2 | = | 1 | ∑n≥b+1 1/2 (n-b-1)(n-b) xn |
| b! | (1-x)3 | b! |
Sumando [13], [14] y [15], en [12] queda:
| (x2 - 3x + 3) xb+2 | = | 2 | ∑n≥b+1 (n-b-1) xn | - |
| b! (1-x)3 | b! |
| - | 1 | ∑n≥b+1 (n-b-2) xn | + | 1 | ∑n≥b+1 1/2 (n-b-1)(n-b) xn | = |
| b! | b! |
Por lo tanto esta parte queda así:
| (x2 - 3x + 3) xb+2 | = ∑n≥b+1 | 1 | ( (n-2b+1)n -b+b2 ) xn |
| b! (1-x)3 | 2 b! |
Ignorar un término de una serie y la delta de Kronecker
En el apartado anterior obtuvimos [13] y [15] con sumatorios que se inician en n≥b+1, algo necesario para poder obtener el término general de la función generadora que estamos utilizando. Pero con [14] apareció el término xb+1 por fuera del sumatorio y no sabemos si podemos ignorarlo y tomar sólo el sumatorio. Veamos esto prescindiendo de 1/b! en [14]:
| xb+3 | = xb+1 + ∑n≥b+1 (n-b-2) xn |
| (1-x)2 |
Particularicemos para un valor concreto b=3:
| x6 | = x4 + ∑n≥4 (n-5) xn |
| (1-x)2 |
Si resolvemos con Wolfram Alpha la parte izquierda (ver WA) o la parte dererecha (ver WA y WA) nos devolverá literalmente estas soluciones, exactamente iguales:
| x6 |
| (1-x)2 |
| = ∑n=-∞∞ | ⎧ | ⎰ | n-5 | n>4 | ⎫ | xn |
| ⎩ | ⎱ | 0 | otherwise | ⎭ |
| = ∑n=-∞∞ | ⎧ | ⎰ | n-5 | n>4 | ⎫ | xn |
| ⎩ | ⎱ | 0 | otherwise | ⎭ |
Esto quiere decir que para n<5 vale cero y para n≥5 vale n-5, con lo que podemos expresarlo así limitando el rango a n≥5:
| x6 | = ∑n≥5 (n-5) xn |
| (1-x)2 |
Se observa que el término general n-5 es el mismo, pero los sumatorios empiezan en n=5 y el nuestro debe empezar en n=4, para poder equipararlo con el sumatorio de la función generadora en n≥b+1, siendo b+1=3+1=4.
En la solución de Wolfram Alpha para el primer valor del rango tenemos:
Mientras que en la nuestra para el primer valor del rango tenemos:
Por lo tanto ambas soluciones parecen equivalentes siempre que no ignoremos x4. Pero vamos a hacer un supuesto ignorándolo y tomando solo el sumatorio ∑n≥4 (n-5) xn en la expresión [17], en tanto que el término general n-5 es el mismo. Y de la misma forma ignorar xb+1 y tomar solo el sumatorio ∑n≥b+1 (n-b-2) xn al obtener la expresión general [14].
El supuesto es que se puede ignorar x4 pues sólo actúa cuando n = 4 = 3+1 = b+1 en el caso base. Para asegurar esta decisión hemos de verificar que no afecta al resto de la suma de la serie. Para ello tenemos que ver como podemos convertir x4 en una serie, para lo que necesitamos el concepto de Delta de Kronecker.
La delta de Kronecker es una función de dos variables, enteros no negativos en este caso, que vale 1 si las dos variables son iguales y 0 en otro caso:
| δi,j = { | 0 | si i≠j |
| 1 | si i=j |
Si tenemos una serie como ∑n≥0 xn = 1 + x + x2 + x3 + ... e introducimos un delta de Kronecker δn,2 con lo que cuando n=2 vale 1 y 0 cuando n≠2, obtendremos:
Podemos aplicar esto a nuestro caso:
Como δn,4 = 1 cuando n=4, entonces n-5+δn,4 = 0 como habíamos obtenido antes. Y cuando n≠4 la delta no tiene ningún efecto sobre el término n-5 pues vale cero. Por lo tanto tal como dijimos antes, el término x4 sólo actua para el valor inicial del rango n=4 y podemos (supuestamente) prescindir del mismo y tomar solo el sumatorio de [17] o [14], para el caso general.
Digo "supuestamente" pues en el siguiente apartado obtendremos la solución final que, si es la que esperamos, entonces este supuesto parece correcto. De no ignorarlo tendríamos que incluir la delta de Kronecker en [16], para lo cual primero revisaremos [14]:
| 1 | ( xb+1 + ∑n≥b+1 (n-b-2) xn ) | = |
| b! |
| = | 1 | ( ∑n≥b+1 δn,b+1 xn + ∑n≥b+1 (n-b-2) xn ) | = |
| b! |
| = | 1 | ∑n≥b+1 (n-b-2+δn,b+1) xn |
| b! |
Quedaría entonces el término general de [16] así:
En el último apartado comprobaremos que tenemos que ignorar ese añadido de la delta de Kronecker.
Componiendo la solución final
En [10] componemos [11] y [16] quedando:
| G(x) = | (1+x)2 | ( ex - ∑n=0..b xn/n! ) | + | (x2 - 3x + 3) xb+2 | = |
| (1-x) | b! (1-x)3 |
| = ∑n≥b+1 ( 4 ( ∑j=b+1..n | n! | ) - n - 3 ) | xn | + |
| j! | n! |
| + ∑n≥b+1 | 1 | ( (n-2b+1)n -b+b2 ) n! | xn | = |
| 2 b! | n! |
| = ∑n≥b+1 ( | 1 | ( (n-2b+1)n -b+b2 ) n! | - (n+3) + 4 ∑j=b+1..n | n! | ) | xn |
| 2 b! | j! | n! |
Extraemos el término general y hacemos un ajuste en el rango del sumatorio con rango j=b+1..n para ponerlo como j=0..n
| T(n, b) = | 1 | ( (n-2b+1)n-b+b2) n! | - (n+3) + 4 ∑j=b+1..n | n! | = |
| 2 b! | j! |
| = | 1 | ( (n-2b+1)n-b+b2) n! | - (n+3) - 4 ∑j=0..b | n! | + 4 ∑j=0..n | n! | = |
| 2 b! | j! | j! |
| = | 1 | ( (n-2b+1)n-b+b2) n! | - (n+3) - | 8 n! | ∑j=0..b | b! | + ∑j=0..n | n! | = |
| 2 b! | 2 b! | j! | j! |
Pasando el término con el sumatorio j=0..b dentro del paréntesis de la iquierda nos queda exactamente la misma solución que alcanzamos en el tema anterior usando otra técnica:
| T(n, b) = | 1 | ( (n-2b+1)n-b+b2-8 ∑j=0..b | b! | ) n! | - (n+3) + 4 ∑j=0..n | n! |
| 2 b! | j! | j! |
En el tema de las variaciones donde obtuvimos esa misma solución usamos la técnica de usar una secuencia de primeros casos base, como expusimos en los primeros apartados. Y la deducción de la solución general con esa técnica en ese tema resultó más fácil de conseguir que todo el desarrollo con función generadora en este tema.
Comprobación del supuesto de ignorar la delta de Kronecker
Si en la solución [19] resolvemos para n=b+1 debemos obtener el resultado T(n, b) = T(b+1, b) = 1 tal como establece el caso base de la recurrencia de partida. Vamos a hacerlo por partes. En el grupo de paréntesis tenemos esto:
El sumatorio de la derecha nos da esto:
| ∑j=0..n | n! | ⇒ ∑j=0..b+1 | (b+1)! | = | (b+1)! | + ∑j=0..b | (b+1)! | = 1 + (b+1) ∑j=0..b | b! |
| j! | j! | (b+1)! | j! | j! |
Poniendo eso en [19]:
| T(b+1, b) = | 1 | ( 2 - 8 ∑j=0..b | b! | ) (b+1)! | - (b+4) + 4 (1 + (b+1) ∑j=0..b | b! | ) = |
| 2 b! | j! | j! |
| = ( 1 - 4 ∑j=0..b | b! | ) (b+1) | - (b+4) + 4 + 4 (b+1) ∑j=0..b | b! | = |
| j! | j! |
| = b + 1 - 4 (b+1) ∑j=0..b | b! | - b + 4 (b+1) ∑j=0..b | b! | = 1 |
| j! | j! |
Hemos obtenido el resultado esperado T(b+1, b) = 1
Al final del apartado anterior dijimos que "supuestamente" debíamos ignorar el término xb+1 que aparecía al obtener [14]. Y dado que sólo afectaba para el caso n=b+1, vemos que estábamos en lo cierto, pues ignorándolo hemos obtenido el resultado esperado. Si no lo hubiésemos ignorado tendríamos que tomar -2 δn,b+1 que vemos en [18] e incluirlo en la solución general [19], formando parte de la expresión que resolvimos en [20], quedando ahora así teniendo en cuenta que δb+1,b+1 = 1
Si esto da cero, el 2 y el 1 con fondo azul del desarrollo anterior resultan cero, con lo que b+1 con fondo azul será también cero y el resultado final será T(b+1, b) = -b, valor no consistente con la recurrencia de partida que declara que T(b+1, b) = 1.