Desarreglos recursivo
Generar desarreglos usando un recursivo
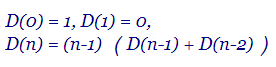
Ya vimos en un tema anterior que los desarreglos (derangement) de una lista con n elementos distintos son todas las sublistas ordenadas con n elementos distintos que se pueden generar de tal forma que ninguno aparece en su posición original. O bien que no tienen puntos fijos. Se denota como D(n). Y también como !n, el subfactorial de n.
En este tema vamos a implementar un segundo algoritmo para generar los desarreglos de una lista con n elementos. Se basa en la primera recurrencia que expusimos en ese tema:
| D(n) = { | 1 | n=0 |
| 0 | n=1 | |
| (n-1) (D(n-1) + D(n-2)) | n≥2 |
De forma compacta podemos poner la recurrencia así:
Intentemos usar este modelo de recurrencia con la lista inicial list = [ a, b, c, d ] con letras, exigiendo que las permutaciones generadas no deben tener ninguna letra en su posición inicial. En algunos caso presentamos para abreviar las listas sin comas para facilitar la escritura, siendo la inicial abcd.
Los desarreglos de esa lista son 9 permutaciones sin puntos fijos siguientes, los mismos que los de la
El objetivo es ver como podemos generar esos desarreglos. Para ello modificaremos algo la recurrencia anterior de esta forma:
Agregamos el caso base D(2)=1, pues con una lista de dos elementos tenemos que D(ab) = ba, por lo que iteramos por la lista inicial abcd tomando como pivote la primera letra y la vamos intercambiando con el resto de letras a la derecha hasta que lleguemos a una lista con dos elementos. Esto produce un bucle en la llamada inicial de n-1 intercambios. Con 4 letras se produce 3 intercambios de la primera letra con las 3 restantes. En el esquema siguiente tenemos el primer intercambio que produce los tres primeros desarreglos de [1]:
list = abcd Call 1 bacd ⇒ D(acd) ⇒ cad ⇒ D(ad) = da ⇒ bcda dca ⇒ D(ca) = ac ⇒ bdac Call 2 bacd ⇒ D(cd) = dc ⇒ badc
En cada iteración del bucle se producen 2 llamadas. En color verde tenemos la primera letra que hace de pivote. Y en rojo la de intercambio. En la primera llamada (Call 1) se produce otra llamada D(acd) con n-1 elementos. Tras lo cual repetimos recursivamente el proceso llegando a una lista con dos elementos D(ad) y D(ca) que los intercambiamos. Finalmente componemos el resultado parcial que es un deasrreglo con las letra pivote, la de intercambio y resultado que aparecen subrayados. Esos dos desarreglos que se obtienen en este paso no tiene ningún punto fijo, es decir, sus letras no ocupan las posiciones iniciales.
En la segunda llamada (Call 2) dentro del mismo primer intercambio tomamos las dos letras restantes (n-2) llamando a D(cd), que tras intercambiarlas nos da otro desarreglo. En esta parte marcamos la letra intercambiada con un sobrerayado a pues esa letra debe mantener su posición en el resultado. En este caso está en segundo lugar al inicio y al final. Nuevamente el resultado parcial no tiene puntos fijos.
El segundo intercambio tiene el siguiente esquema, donde se observa como la letra a mantiene la tercera posición al inicio y al final de Call 2, con lo que queda intercalada en el resultado parcial db:
list = abcd Call 1 cbad ⇒ D(bad) ⇒ abd ⇒ D(bd) = db ⇒ cadb dab ⇒ D(ab) = ba ⇒ cdba Call 2 cbad ⇒ D(bd) = db ⇒ cdab
Y el último intercambio, con a manteniendo la cuarta posición al inicial y al final de la llamada Call 2:
list = abcd Call 1 dbca ⇒ D(bca) ⇒ cba ⇒ D(ba) = ab ⇒ dcab acb ⇒ D(cb) = bc ⇒ dabc Call 2 dbca ⇒ D(bc) = cb ⇒ dcba
Al final obtenemos los desarreglos que vimos en [1]. Este proceso recursivo, que puede hacerse manualmente, podemos convertirlo en un algoritmo como veremos a continuación.
Segundo algoritmo para generar desarreglos derange2(list)
En los esquemas que vimos antes llegábamos al caso base cuando teníamos una lista con 2 elementos para simplificar la exposición, sin contemplar que podríamos llegar a casos base con menos elementos que son los que vemos en la recurrencia matemática que ya expusimos:
| D(n) = { | 1 | n=0 |
| 0 | n=1 | |
| (n-1) (D(n-1) + D(n-2)) | n≥2 |
Y de forma compacta:
Teniendo en cuenta esto, el primer esquema que produce los tres primeros resultados bcda, bdac, badc de los desarreglos de una lista abcd debería ser así:
list = abcd Call 1 bacd ⇒ D(acd) cad ⇒ D(ad) da ⇒ D(a) = [] ⭢ da ⭢ cda ⭢ bcda dca ⇒ D(ca) ac ⇒ D(c) = [] ⭢ ac ⭢ dac ⭢ bdac Call 2 bacd ⇒ D(cd) dc ⇒ D(∅) = [[]] ⭢ dc ⭢ badc
Se observa que en la primera llamada llegamos a casos base con 1 elemento, como D(a) y D(c). En la segunda llamada en cambio llegamos a un caso base con 0 elementos con lo que la última llamada será D(∅). Los retornos en color azul de las llamadas se producen con estas últimas, componiéndose finalmente los tres resultados esperados para este primer esquema. De igual forma haríamos con los otros dos esquemas.
Esto se implementa en este algoritmo:
// D(0)=1, D(1)=0, D(n) = (n-1) × (D(n-1) + D(n-2))
function derange2(list=[]){
let n = list.length;
let result = [];
if (n===0) {
//iter += 1;
result = [[]];
} else if (n===1) {
//iter += 1;
result = [];
/*} else if (n===2) {
result = [[list[1], list[0]]];*/
} else {
//iter += 1;
for (let j=1; j<n; j++){
//iter += 1;
let pivot = list[j];
let swap = list[0];
//iter += (n-2);
let listMinor = [...list.slice(1, j), swap,
...list.slice(j+1)];
let subResult = derange2(listMinor);
/* subResult.length = !(n-1) */
for (let i=0; i<subResult.length; i++){
/* subResult[i].length = (n-1) */
//iter += 1 + subResult[i].length;
result.push([pivot, ...subResult[i]]);
}
//iter += (n-2);
listMinor = [...list.slice(1, j), ...list.slice(j+1)];
subResult = derange2(listMinor);
/* subResult.length = !(n-2) */
for (let i=0; i<subResult.length; i++){
/* subResult[i].length = (n-2) */
//iter += 1 + subResult[i].length;
result.push([pivot, ...subResult[i].slice(0, j-1), swap,
...subResult[i].slice(j-1)]);
}
}
}
return result;
}Como siempre aparecen comentadas las sentencias con iter, que son las que cuentan las iteraciones y que en la aplicación Combine Tool las descomento. Además tenemos también comentado el caso base n=2, en cuyo caso devolverá la lista con 2 elementos invertida, cuyo coste también podemos considerar unitario. Ejecutando el algoritmo sin y con el caso base n=2 obtenemos el siguiente conteo de iteraciones:
| n | !n | Iter n≤1 | Iter n≤2 | % reducción |
|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 0.00 |
| 1 | 0 | 1 | 1 | 0.00 |
| 2 | 1 | 5 | 1 | 80.00 |
| 3 | 2 | 25 | 17 | 32.00 |
| 4 | 9 | 139 | 103 | 25.90 |
| 5 | 44 | 897 | 721 | 19.62 |
| 6 | 265 | 6771 | 5711 | 15.65 |
| 7 | 1854 | 58 789 | 51 373 | 12.61 |
| 8 | 14 833 | 575 821 | 516 489 | 10.30 |
| 9 | 133 496 | 6 263 633 | 5 729 649 | 8.53 |
| 10 | 1 334 961 | 74 771 353 | 69 431 509 | 7.14 |
La reducción en % que se consigue agregando el caso base n=2 es alto para valores bajos de n, pero en números absolutos representan muy pocas iteraciones. A medida que incrementamos el tamaño de la lista inicial baja muy rapidamente este porcentaje, aunque en valor absoluto no es despreciable. Por ejemplo, para n=10 tenemos una diferencia de 5 339 844 iteraciones pero solo representa un 7.14 %. Con objeto de seguir la recurrencia matemática que vimos y luego analizar mejor el coste del algoritmo, finalmente implementamos omitiendo este caso base n=2. Pero para un uso final en producción podría usarse también ese caso base, especialmente si vamos a trabajar con valores mayores de n.
El algoritmo usa el mismo principio de recorte de lista con el método de JavaScript slice que ya habíamos usado en el primer algoritmo de las permutaciones. Este recorte con slice es costoso, pero la ventaja es que no modifica la lista inicial y además no es necesario copiar los resultados, pues slice crea siempre un nuevo Array.
El bucle itera en n-1 elementos en el rango j=1..n-1. Intercambiamos el primer elemento con swap = list[0], mientras que el pivote es pivot = list[j]. La primera llamada se hace con la lista recortada de tamaño n-1, intercambiando pivote (pivot) por intercambio (swap). A la vuelta componemos los subresultados anteponiendo el pivote al subresultado.
Para la segunda llamada recortamos quitando el intercambio, lo que producirá una lista menor de tamaño n-2. A la vuelta componemos con pivote (pivot) al inicio e intercambio (swap) entre las partes de cada subresultado delimitadas por el índice j.
Planteamiento del Coste del algoritmo para generar desarreglos
Basándonos en los comentarios iter que cuentan iteraciones en el algoritmo, para n≥1 pasamos a plantear la recurrencia. Explicamos este coste (ver más en el coste de los recursivos) observando las instrucciones iter y comentarios en el algoritmo que se corresponde con el orden izquierda a derecha de la expresión anterior, observando todo lo que está en la parte recursiva dentro de la alternativa else:
- Sumamos 1 a la entrada por cada vez que ejecutemos este trozo
else - Multiplicamos n-1 iteraciones que tiene el bucle externo
for (let j=1; j<n; j++), cuyo interior tiene este coste:- Sumamos 1 a la entrada del bucle (siempre a la entrada de un bucle sumaremos uno)
- Sumamos n-2 que es el coste de recortar y propagar la lista en dos trozos
...list.slice(1, j)y...list.slice(j+1)que supone iterar en total n-2 posiciones. Consideramos que insertar la variableswapen el Array y componer ese Array tiene coste unitario, que se combina en secuencia con el+1de la cabecera del bucle. Vea que esa línea de códigolet listMinor = [...list.slice(1, j), swap, ...list.slice(j+1)]puede ser sustituido por esto:let listMinor = []; for (let k=1; k<=j-1; k++){ iter += 1; listMinor.push(list[k]); } listMinor.push(swap); for (let k=j+1; k<=n-1; k++){ iter += 1; listMinor.push(list[k]); }El primer bucle tiene una longitud de (j-1)-1+1=j-1 y el segundo de (n-1)-(j+1)+1=n-j-1. Declarar el Array y elpush()exterior tienen costes unitarios que se combinan en secuencia con su cabecera (eliter += 1al inicio del bucle exterior) y lo podemos omitir aquí. Usarpush()dentro de los bucles tienen costes unitarios, con lo que el coste final es es (j-1) × 1 + (n-j-1) × 1 = n-2 - Sumamos T(n-1) de la primera llamada recursiva
- Sumamos !(n-1) n, pues en
subResulttendremos un subresultado cuya longitud es el subfactorial !(n-1), pues es la devolución a la llamada que hicimos con T(n-1) que tendrá que devolver ese número de desarreglos. Por cada subresultado o desarreglo componemos un Array con la variablepivotpropagandosubResult[i]que tiene una longitud n-1. Insertarpivoten el nuevo Array no aportará coste. Podemos comprobar este trozo/* subResult.length = !(n-1) */ for (let i=0; i<subResult.length; i++){ /* subResult[i].length = (n-1) */ //iter += 1 + subResult[i].length; result.push([pivot, ...subResult[i]]); }si lo expresamos así:// subResult.length = !(n-1) for (let i=0; i<=subResult.length; i++) iter += 1; let arr = [pivot]; // subResult[i].length = n-1 for (let k=0; k<subResult[i].length; k++ { iter += 1; arr.push(subResult[i][k]); }) }Como declarar un array con un número definido y constante de posiciones y usarpushtienen costes unitarios que se acumulan en secuencia con la cabeceraiter += 1, entonces el coste total es !(n-1) × (1 + ((n-1) × 1)) = !(n-1) n. - Para no extendernos, la segunda parte relacionada con la segunda llamada se analiza de forma similar teniendo el coste (n-2) + T(n-2) + !(n-2) (n-1)
Agrupando todo y poniendo los casos bases llegamos a esta recurrencia:
T(n) = 1 + (n-1) ( 1 + (n-2) + T(n-1) + !(n-1) n + (n-2) + T(n-2) + !(n-2) (n-1) )
Hay veces que conseguimos que WolframAlpha resuelva las recurrencias. Al menos si no devolviendo la solución (con la versión gratuita), si al menos la secuencia de resultados, pues devuelve para n≥0 la secuencia siguiente:
que coincide con la que obtuvimos en la tabla de valores del apartado anterior, valores obtenidos ejecutando este algoritmo derange2(list) en la herramienta Combine Tool.
Con la tranquilidad de que la recurrencia traduce correctamente el contaje de interaciones del algoritimo, pasamos a simplificarla. Empezamos pasando n-1 dentro del paréntesis:
(n-1) ( !(n-1) n + !(n-2) (n-1) )
Expandimos el polinomio central
T(n) = (n-1) T(n-1) + (n-1) T(n-2) + 2n2-5n+4 + (n-1)(!(n-1) n + !(n-2) (n-1))
Puede comprobarse en WolframAlpha su corrección al obtener la misma secuencia obtenida T(n) = 1, 1, 5, 25, 139, ...
Coste del algoritmo para generar desarreglos
Partiendo de la recurrencia obtenida antes incrementamos 2 índices para evitar negativos
(n-1)(!(n-1) n + !(n-2) (n-1))
Dividimos todo por n+1 y obtenemos la recurrencia de partida para aplicar la técnica de la función generadora:
| T(n+2) | = T(n+1) + T(n) + | 2n2 + 3n + 2 | + !(n+1) (n+2) + !n (n+1) |
| n+1 | n+1 |
Puede comprobarse en WolframAlpha su corrección al obtener la misma secuencia obtenida T(n) = 1, 1, 5, 25, 139, ...
Usaremos la función generadora exponencial:
| G(x) = ∑n≥0 T(n) | xn |
| n! |
El índice del sumatorio empieza en el menor caso base que alcance la recurrencia cuando partimos de valores de n que no sean casos base, tal como explicamos en el tema desplazamiento de caso base. Por lo tanto aquí será n=0.
Las condiciones particulares son las siguientes, recordando que T(0) = 1 y T(1) = 1
| G0(x) = ∑n=0..0 T(n) | xn | = T(0) | x0 | = 1 × 1 = 1 |
| n! | 0! |
| G1(x) = ∑n=1..1 T(n) | xn | = T(1) | x1 | = 1 × x = x |
| n! | 1! |
Aplicamos la fución generadora a la recurrencia término a término desde la izquierda:
El primero en [2] es:
∑n≥0 T(n+2) xn = ∑n≥0 T(n+2) xn = n+1 n! (n+1)! = ∑n≥0 T(n+2) (n+2) xn = (n+2)! = ∑n≥0 T(n+2) (n+2) xn+2 x-2 = (n+2)! = 1 ∑n≥0 T(n+2) (n+2) xn+2 = x2 (n+2)! = 1 ∑n≥2 T(n) n xn = x2 n! = 1 ( - ∑n=1..1 T(n) n xn + ∑n≥1 T(n) n xn ) = x2 n! n! = 1 ( - T(1) 1 x1 + ∑n≥1 T(n) n xn ) = x2 1! n! = 1 ( - x + ∑n≥1 T(n) n xn ) = x2 n! = 1 ( - x + x G'(x) ) = x2 = 1 ( - 1+ G'(x) ) x Para resolver [4] echamos mano de derivadas e integrales de una serie que dice que si A(x) es la función generadora de la serie ∑n≥0 an xn, donde A'(x) es su derivada, entonces se cumple x A'(x) = ∑n≥1 n an xn. Por lo tanto podemos identificar an = T(n)/n! así como su función generadora G(x) = ∑n≥0 T(n)/n! xn con lo que estaremos en el caso dado.
El segundo en [2] es:
∑n≥0 T(n+1) xn = ∑n≥0 (n+1) T(n+1) xn= G'(x) n! (n+1)! Esto es parecido a lo visto en la entrada anterior. Además ya lo resolvimos un el tema anterior en el párrafo derivadas de una serie y que también explicamos en derivadas e integrales de una serie. Se basa en el principio de que si A(x) es la función generadora de la serie ∑n≥0 an xn, donde A'(x) es su derivada, entonces se cumple: A'(x) = ∑n≥0 (n+1) an+1 xn
Solo basta multiplicar y dividir por n+1 e identificar an = T(n)/n!, siendo su función generadora G(x) = ∑n≥0 T(n)/n! xn la que estamos usando, con lo que podemos equipararlo con lo anterior.
El tercero en [2] es la propia función generadora de la que partimos:
∑n≥0 T(n) xn = G(x) n! El cuarto en [2] es:
∑n≥0 2n2 + 3n + 2 × xn = ex (2x2+x+1) - 1 n+1 n! x Lo hemos obtenido directamente desde WolframAlpha, pudiendo ver como se obtiene también en el siguiente desplegable.
Y para ver el último en [2] antes vemos esto, que se basa en los subfactoriales:
!(n+1) = ∑k=0..n+1 (-1)k (n+1)! = k! = (n+1) ∑k=0..n+1 (-1)k n! = k! = (n+1) (-1)n+1 n! + (n+1) ∑k=0..n (-1)k n! = (n+1)! k! = (-1)n+1 + (n+1) !nEntonces usamos esto para resolver la parte de la derecha en [2] que contiene los subfactoriales
∑n≥0 (!(n+1) (n+2) + !n (n+1)) xn = n! = ∑n≥0 (!(n+1) (n+1) + !(n+1) + (n+1) !n) xn = n! = ∑n≥0 (!(n+1) (n+1) + (-1)n+1 + (n+1) !n + (n+1) !n) xn = n! = ∑n≥0 (!(n+1) (n+1) + (-1)n+1 + 2(n+1) !n) xn = n! = ∑n≥0 (!(n+1) (n+1) + (-1)n+1 + 2 n !n + 2 !n) xn n! Veamos cada parte empezando por el más sencillo, empezando por la derecha:
La cuarta
2 ∑n≥0 !n xn = 2 e-x n! 1-x Esto es así como vimos en el tema anterior al definir el subfactorial.
La tercera
2 ∑n≥0 n !n xn = 2 e-x x2 n! (1-x)2 Aquí aplicamos lo que vimos antes sobre derivadas de una serie. Si tenemos el término general an de una sucesión y A(x) = ∑n≥0 an xn es su función generadora, entonces se cumple x A'(x) = ∑n≥1 n an xn. Identificamos:
an = !n/n!A(x) = ∑n≥0 an xn ⇒ e-x/(1-x) = ∑n≥0 !n/n! xnx A'(x) = ∑n≥1 n an xn ⇒Por un lado
x ( d e-x ) = e-x x2 dx 1-x (1-x)2 Entonces
e-x x2 = ∑n≥1 n !n xn =- 0 !0 x0 + ∑n≥0 n !n xn (1-x)2 n! 0! n! La segunda
∑n≥0 (-1)n+1 xn = - ∑n≥0 (-1)n xn = - ∑n≥0 (-x)n = - e-x n! n! n! La primera
∑n≥0 (n+1) !(n+1) xn = e-x (x3-x2+2x) n! (1-x)3 Esto es así porque antes vimos en [11] que
e-x x2 = ∑n≥0 n !n xn = ∑n≥0 !n xn (1-x)2 n! (n-1)! Por lo tanto si tenemos el término general an = !n/(n-1)! y su función generadora es A(x) = e-x x2 / (1-x)2, aplicando derivadas e integrales de una serie que dice que si A'(x) es la derivada de la función generadora de la serie ∑n≥0 (n+1) an+1 xn entonces se cumple A'(x) = ∑n≥0 (n+1) an+1 xn. Aplicando a nuestro caso
∑n≥0 (n+1) !(n+1) xn = ∑n≥0 (n+1) !(n+1) xn n! n! donde se observa que si an = !n/(n-1)! entonces an+1 = !(n+1)/n! entonces la solución es A'(x)
A'(x) = d e-x x2 = e-x (x3-x2+2x) dx (1-x)2 (1-x)3
Agrupando desde [6] a [13] en la disposición de [2]
| 1 | (G'(x) - 1) = G'(x) + G(x) + | 1 | ( ex (2x2+x+1) - 1 ) + | 2 e-x | + |
| x | x | 1-x |
| + | 2 e-x x2 | - e-x + | e-x (x3-x2+2x) |
| (1-x)2 | (1-x)3 |
Pasando x al otro lado
| G'(x) - 1 = x G'(x) + x G(x) + ex (2x2+x+1) - 1 + | 2 x e-x | + |
| 1-x |
| + | 2 x e-x x2 | - x e-x + | x e-x (x3-x2+2x) |
| (1-x)2 | (1-x)3 |
Pasando G'(x) a la izquierda y anulando -1 en ambos lados:
| (1-x) G'(x) = x G(x) + ex (2x2+x+1) + | 2 x e-x | + |
| 1-x |
| + | 2 x e-x x2 | - x e-x + | x e-x (x3-x2+2x) |
| (1-x)2 | (1-x)3 |
Dividiendo todo por 1-x y pasando G(x) a la izquierda
| G'(x) - | x | G(x) = | ex (2x2+x+1) | + | e-x 2x | + |
| 1-x | 1-x | (1-x)2 |
| + | e-x 2x3 | - | e-x x | + | e-x (x4-x3+2x2) |
| (1-x)3 | 1-x | (1-x)4 |
Esto es una ecuación diferencial lineal ordinaria con coeficientes variables de primer orden, no homogénea en este caso. La homogénea ya la vimos en el tema anterior para el subfactorial, con solución:
| G'(x) - | x | G(x) = 0 ⇒ G(x) = | e-x | = | 1 |
| 1-x | 1-x | ex (1-x) |
Si la parte derecha de [14] la denominamos g(x) y multiplicamos por la recíproca de esa solución homogénea que es ex (1-x)
Como la derivada de la recíproca multiplicado por G(x) resulta
| d | ex (1-x) G(x) = ex (1-x) G'(x) - ex x G(x) |
| dx |
en algo que es igual que la parte izquierda de [15], entonces igualamos la derivada con la parte derecha que contiene g(x) queda
| d | ex (1-x) G(x) = ex (1-x) g(x) |
| dx |
Así que integrando ambos lados podemos obtener G(x):
Integramos cada parte de g(x) (parte derecha de [14]) multiplicado por ex (1-x)
| ∫( | 2x | ) dx | = - 2x - 2 log(x-1) + c |
| 1-x |
| ∫( | 2x3 | ) dx | = x2 + 4x + | 2 | + 6 log(x-1) + c |
| (1-x)2 | 1-x |
| ∫( | x4-x3+2x2 | ) dx | = - 1/2 x2 - 2x - | 5 | + | 1 | - 5 log(x-1) + 5/2 + c |
| (1-x)3 | 1-x | (1-x)2 |
Sustituyendo en [16] a la vez que simplificamos, agregando una constante que acumula la de las integrales:
| ex (1-x) G(x) = 1/4 e(2x) (4x2 - 2x + 3) - | 3 | + | 1 | - log(x-1) + 5/2 + c |
| 1-x | (1-x)2 |
Despejando G(x) y agrupando 5/2 + c como una constante tenemos la función generadora
| G(x) = | ex (4x2 - 2x + 3) | + | 1 | - | 3 e-x | + | e-x | - | e-x log(x-1) | + | e-x (5/2+c) |
| 4(1-x) | 1-x | (1-x)2 | (1-x)3 | 1-x | 1-x |
Busquemos las series de cada término:
ex (4x2 - 2x + 3) = ex x2 - 1/2 ex x + 3/4 ex = 4(1-x) 1-x 1-x 1-x = ∑n≥0 ( ∑j=0..n-2 n! ) xn + j! n! - 1/2 ∑n≥0 ( ∑j=0..n-1 n! ) xn + j! n! + 3/4 ∑n≥0 ( ∑j=0..n n! ) xn = j! n! = ∑n≥0 ( - 1/2 (2n+1) + 5/4 ∑j=0..n n! ) xn j! n! Se obtiene centrándonos en el término general que se puede simplificar así:
∑j=0..n-2 n! - 1/2 ∑j=0..n-1 n! + 3/4 ∑j=0..n n! = j! j! j! = ( 1 - 1 + 3 ) ∑j=0..n n! - ∑j=n-1..n n! + 1 ∑j=n..n n! = 2 4 j! j! 2 j! = - 1/2 (2n+1) + 5/4 ∑j=0..n n! j! En el tema de las permutaciones resolvimos una expresión que contenía la misma descomposición en fracciones. En el fondo se basa en lo que vimos en el tema de las K-Tuplas:
G(x, k) = xk ex = ∑n≥0 ( ∑j=0..n-k n! ) xn 1-x j! n! -3 e-x = ∑n≥0 -3 ( !n + !(n+1) ) xn (1-x)2 n! Esto lo obtuvimos en el tema anterior sobre generando subfactoriales
e-x = ∑n≥0 ( ½ (n+2) !n + ½ (n+3) !(n+1) ) xn (1-x)3 n! Esto también lo obtuvimos en ese tema anterior
- e-x log(x-1) = ∑n≥0 A(n) xn 1-x n! Esta función generadora con un logaritmo es un reto díficil. Por el momento supongamos que existe el término general A(n), que después intentaremos encontrar de una forma indirecta. En el tema siguiente sobre subfactoriales y logaritmos volveremos sobre esto.
(5/2+c) e-x = (5/2+c) ∑n≥0 !n xn (1-x) n! Esto lo obtuvimos en el tema del subfactorial.
Sumando todo:
| T(n) = - 1/2 (2n+1) + 5/4 ∑j=0..n | n! | - 3 !n - 3 !(n+1) + |
| j! |
Con lo que tenemos una primera fórmula del coste de la recurrencia, aunque aún pendiente de determinar la constante c y el término A(n):
| 5/4 ∑j=0..n | n! | + 1/2 (n+1) !n + 1/2 (n-3) !(n+1) + c !n + A(n) |
| j! |
Descubriendo la constante
En la resolución de recurrencias donde aparecen ecuaciones diferenciales como esta que hemos visto, aparecerán constantes que hemos de determinar. Además en este caso tenemos el término A(n) desconocido, pues la función contenía un logaritmo que por ahora estamos evitando resolver. En este apartado buscaremos una forma indirecta de resolverlo, aunque en un siguiente tema sobre subfactoriales y logaritmos nos enfrentaremos con eso.
Si definimos T(n) = T1(n) + T2(n) tenemos la parte conocida
| T1(n) = -1/2 (2n+1) + 5/4 ∑j=0..n | n! | + 1/2 (n+1) !n + 1/2 (n-3) !(n+1) |
| j! |
y la parte desconocida
En WolframAlpha obtenemos la secuencia para n≥1 siguiente para T1(n)
Le agregamos el valor n=0 que resulta ser 5/4, viéndose que todos los términos dividen por 4:
Con el planteamiento de la recurrencia habíamos obtenido la secuencia para n≥0 siguiente también en WolframAlpha, que coincidía con el recuento de iteraciones en nuestro algoritmo, con lo que esta secuencia es la que debemos obtener en la solución:
Como A(n) es un término desconocido hagámos la suposición que A(0) = 0, con objeto de determinar la constante c usando los valores iniciales T(0) = 1 y T1(0) = 5/4 que conocemos:
Con esto también debe cumplirse la segunda condición inicial T(1) = 1 y T1(1) = 0/4, con lo que podemos determinar el segundo término A(1)
Así que hemos de encontrar el término desconocido como una secuencia que empieza con A(n) = 0, 1, ... Vamos a incluir la constante c = -1/4 en la fórmula de T1(n) que denominaremos Tc(n) = T1(n) + c
| -1/2 (2n+1) + 5/4 ∑j=0..n | n! | + 1/2 (n+1) !n + 1/2 (n-3) !(n+1) - 1/4 !n |
| j! |
Obtenemos en WolframAlpha la secuencia siguiente, a la que hemos agregado el valor para n=0
La diferencia entre ambos términos T(n)-Tc(n) es A(n)
n T(n) Tc(n) A(n)=T(n)-Tc(n)
----------------------------------
0 1 1 0
1 1 0 1
2 5 4 1
3 25 20 5
4 139 119 20
5 897 788 109
6 6771 6082 689
7 58789 53736 5053
8 575821 533773 42048
Entonces tenemos la secuencia
para la que hemos de encontrar una fórmula. Se observa que cumple lo que impusimos A(0) = 0 y A(1) = 1. Usando OEIS encontramos precisamente esa secuencia con el término general siguiente:
donde H(j) es el j-ésimo número armónico. En Wikipedia vemos que
Da lugar a esta secuencia:
Wolfram Alpha no expande en valores la fórmula de A(n), al menos con la versión gratuita. Pero podemos obtener valores individuales en WolframAlpha, como, por ejemplo, A(3) = 3 H(1) - 6 H(2) + 6 H(3) que podemos resolver en un segundo paso en WolframAlpha resultando A(3) = 5, pues tomando los números armónicos H(n) como vimos antes, tenemos 3 H(1) - 6 H(2) + 6 H(3) = 3×1/1 - 6×3/2 + 6×11/6 = 5
Usando lo mismo que hicimos con A(3) buscamos los primeros valores, donde observamos que obtenemos la secuencia esperada A(n) = 0, 1, 1, 5, 20, 109, 689, 5053, 42048, ...
n A(n) ------------------ 0 0 1 1 = H(1) 2 1 = 2 H(2) - 2 H(1) 3 5 = 3 H(1) - 6 H(2) + 6 H(3) 4 20 = -4 H(1) + 12 H(2) - 24 H(3) + 24 H(4) 5 106 = 5 H(1) - 20 H(2) + 60 H(3) - 120 H(4) + 120 H(5) 6 689 = -6 H(1) + 30 H(2) - 120 H(3) + 360 H(4) - 720 H(5) + 720 H(6) 7 5053 = 7 H(1) - 42 H(2) + 210 H(3) - 840 H(4) + 2520 H(5) - 5040 H(6) + 5040 H(7) 8 42048 = -8 H(1) - 56 H(2) + 336 H(3) - 1680 H(4) + 6720 H(5) - 20160 H(6) + 40320 H(7) - 40320 H(8)
Volviendo a [18] donde ponemos c = - 1/4 y el término A(n) que vimos en [19] nos queda la solución buscada de la recurrencia:
| T(n) = -1/2 (2n+1) + 5/4 ∑j=0..n | n! | + 1/2 (n+1) !n + |
| j! |
Intentaremos simplifcarlo agrupando lo que multiplica a !n quedando
| + 5/4 ∑j=0..n | n! | + ∑j=1..n (-1)n-j C(n, j) j! H(j) |
| j! |
y a continuación reagrupamos los dos términos que tienen el factor 2n+1
| + 5/4 ∑j=0..n | n! | + ∑j=1..n (-1)n-j C(n, j) j! H(j) |
| j! |
Intentaremos unificar los dos sumatorios, tomando el sumatorio de la derecha
| = ∑j=1..n (-1)n-j | n! | j! H(j) = |
| j! (n-j)! |
| = ∑j=1..n | (-1)n-j n! | H(j) = |
| (n-j)! |
| = | (-1)n-1 n! H(1) | + | (-1)n-2 n! H(2) | +... | + | (-1)1 n! H(n-1) | + | (-1)0 n! H(n) | = |
| (n-1)! | (n-2)! | 1! | 0! |
| = | (-1)0 n! H(n) | + | (-1)1 n! H(n-1) | +... | + | (-1)n-2 n! H(2) | + | (-1)n-1 n! H(1) | = |
| 0! | 1! | (n-2)! | (n-1)! |
| = ∑j=0..n-1 | (-1) j n! | H(n-j) |
| j! |
Al desplegar e invertir los términos de la suma vemos que es lo mismo que la última expresión. Entonces con esto
| 5/4 ∑j=0..n | n! | + ∑j=1..n (-1)n-j C(n, j) j! H(j) | = |
| j! |
| = 5/4 ∑j=0..n | n! | + ∑j=0..n-1 | (-1) j n! | H(n-j) = |
| j! | j! |
| = 5/4 + 5/4 ∑j=0..n-1 | n! | + ∑j=0..n-1 | (-1) j n! | H(n-j) = |
| j! | j! |
| = 5/4 + ∑j=0..n-1 | n! | ( 5/4 + (-1) j H(n-j)) |
| j! |
| = 5/4 + 1/4 ∑j=0..n-1 | n! | ( 5 + 4 (-1) j H(n-j)) |
| j! |
Hemos ajustado el primer sumatorio para que tenga el mismo rango que el segundo, para poder unificar los dos. Finalmente poniendo esto en la última expresión de T(n) en [20] nos queda la solución de la recurrencia
| T(n) = | (2n+1) (!n-2) + 5 | + | (n-3) !(n+1) | + | 1 | ∑j=0..n-1 | n! | ( 5 + 4 (-1) j H(n-j)) |
| 4 | 2 | 4 | j! |
Esta fórmula es la que usamos en la aplicación Combine Tools generando la secuencia T(n) = 1, 1, 5, 25, 139, 897, 6771, 58789, 575821, 6263633, ... que coincide con el contaje de iteraciones.
Como en el caso de las permutaciones, el algoritmo usa el método de recorte de Arrays con slice() que evita tener que hacer copias de los subresultados, con lo que el coste con copia y sin copia es el mismo.
Analizando coste de algoritmos derange1(list) y derange2(list)
Para generar desarreglos hemos implementado derange1(list) que utilizaba directamente el algoritmo de intercambio de Heap permute3(list). Y en este tema derange2(list) que está basado en el algoritmo permute1(list), el primero que implementamos para generar permutaciones y que se basa en recortar listas.
La siguiente tabla muestra el coste de ambos algoritmos:
| n | T(n) | |
|---|---|---|
derange1(list) | derange2(list) | |
| 0 | 3 | 1 |
| 1 | 4 | 1 |
| 2 | 11 | 5 |
| 3 | 39 | 25 |
| 4 | 173 | 139 |
| 5 | 943 | 897 |
| 6 | 6115 | 6771 |
| 7 | 45993 | 58789 |
| 8 | 393433 | 575821 |
| 9 | 3770283 | 6263633 |
El que usa el algoritmo de Heap derange1(list) mejora el de recorte de listas derange2(list) para n≥6. Y cuanto más grande es la lista, mayor es la mejora.