Multinomiales mejorado
Mejorar el coste del algoritmo de Heap para construir permutaciones con repetición
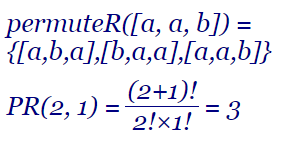
El algoritmo de Heap es un algoritmo de intercambio que supone la forma más eficiente de construir las permutaciones sin repetición. Ese mismo algoritmo lo usamos en el tema anterior para construir las permutaciones con repetición o multinomiales.
Pero el coste parece excesivo. Por ejemplo, para el conjunto de partida A = { a, a, a, a, a, a, a } con 7 letras "a" repetidas, el coste es de 57638 iteraciones. Son muchas iteraciones en tanto que las permutaciones con repetición de A es una, el propio A. Tiene que haber alguna forma de reducir este coste.
Analizando el algoritmo de Heap observamos los intercambios que se producen dentro del bucle. Itera por la lista de partida y va intercambiando elementos, lo que está ideado para elementos distintos. Podríamos evitar intercambio cuando los dos elementos a intercambiar son iguales, pues va a producir una permutación que ya existe. Para ello filtramos con if (j===n-1 || list[j]!==list[n-1]) para intercambiar sólo el primer elemento consigo mismo o cuando son distintos. En cada bucle intercambiamos el elemento de la derecha en la lista consigo mismo con objeto de permutar ese resultado parcial. La comparación del resto de elementos solo se permutan si son distintos, en cuyo caso se intercambian.
function permuteR2(list=[], n=list.length, result=[]){
if (n<=1) {
//iter += 1;
if (!includesArray(result, list)) {
//if (withCopyCost) iter += list.length;
result.push(copy(list));
}
} else {
//iter += 1;
for (let j=n-1; j>-1; j--){
//iter += 1;
if (j===n-1 || list[j]!==list[n-1]) {
[list[j], list[n-1]] = [list[n-1], list[j]];
permuteR2(list, n-1, result);
[list[j], list[n-1]] = [list[n-1], list[j]];
}
}
}
return result;
}Al igual que en el algoritmo que vimos en el tema anterior, necesitaremos la función auxiliar includesArray() para comprobar si ya tenemos un resultado parcial almacenado en los resultados:
// Implement Array.includes() function to count iterations.
function includesArray(result=[], list=[]){
let included = false;
//iter += list.length;
let listString = list.join(",");
if (!Array.isArray(result.value)) result.value = [];
for (let i=0; i<result.value.length; i++){
//iter += 1;
if (result.value[i]===listString){
included = true;
break;
}
}
if (!included) result.value.push(listString);
return included;
}Además ahora vamos a necesitar otra función auxiliar más. Se trata de ordenar una lista inicial como { a, a, a, a, b, b, c } en orden de elementos repetidos ascendente quedando { c, b, b, a, a, a, a }:
function sortRepAsc(list=[]){
//iterSort++;
let obj = {};
for (let item of list) {
iterSort++;
if (!obj.hasOwnProperty(item)) obj[item] = 0;
obj[item]++;
}
let keys = Object.keys(obj).sort((v, w) => {
//iterSort++;
return obj[v]<obj[w] ? -1 : 1;
});
list = [];
for (let key of keys) {
//iterSort++;
for (let i=1; i<=obj[key]; i++) {
//iterSort++;
list.push(key);
}
}
return list;
}Aplicaríamos este ordenamiento antes de ejecutar permuteR2(list). Es un ordenamiento que mejora el coste, pues si empezamos por las elementos que menos se repiten almacenaremos resultados parciales con anticipación. Consideremos como ejemplo que la lista inicial es { a, a, c } y que debe producir las permutaciones con repetición { {a,a,c}, {a,c,a}, {c,a,a} }. Si no ordenamos inicialmente tendríamos esta traza, donde se observa que si el resultado parcial list no existe en la lista final result entonces la incluimos:
| list | result | includesArray (result, list) |
|---|---|---|
| [a,a,c] | [] | false ⇒ result.push(list) = [[a,a,c]] |
| [a,c,a] | [[a,a,c]] | false ⇒ result.push(list) = [[a,a,c], [a,c,a]] |
| [c,a,a] | [[a,a,c], [a,c,a]] | false ⇒ result.push(list) = [[a,a,c], [a,c,a], [c,a,a]] |
| [c,a,a] | [[a,a,c], [a,c,a], [c,a,a]] | true |
| [a,c,a] | [[a,a,c], [a,c,a], [c,a,a]] | true |
En cambio, si ordenamos inicialmente como { c, a, a } tendremos esta traza, evitando los dos últimos resultados parciales que ya existen en la lista final:
| list | result | includesArray (result, list) |
|---|---|---|
| [c,a,a] | [] | false ⇒ result.push(list) = [[c,a,a]] |
| [a,c,a] | [[c,a,a]] | false ⇒ result.push(list) = [[c,a,a], [a,c,a]] |
| [a,a,c] | [[c,a,a], [a,c,a]] | false ⇒ result.push(list) = [[c,a,a], [a,c,a], [a,a,c]] |
El coste del ordenamiento inicial no es muy alto comparado con el coste total, como veremos después. Hay otro efecto que considerar y es que la lista final sale ordenada al revés, pues en el primer caso sin ordenar obtenemos { {a,a,c}, {a,c,a}, {c,a,a} } y en el segundo ordenado obtenemos { {c, a, a}, {a, c, a}, {a, a, c} }.
Tomando algunas listas de muestra ejecutamos permuteR1(list) que vimos en el tema anterior con el coste obtenido de la fórmula y las iteraciones que resultan en la aplicación Combine Tools para permuteR2(list):
| Muestra | permuteR1 (fórmula) | Iteraciones | % reducción | ||||
|---|---|---|---|---|---|---|---|
| permuteR2 sin includes | +includes | Suma | +sort | Suma | |||
| a,a,a,a,a,a,a | 57638 | 34 | 7 | 41 | 16 | 57 | 99.9 % |
| a,a,a,a,a,a,b | 72752 | 105 | 70 | 175 | 18 | 193 | 99.7 % |
| a,a,a,a,a,b,b | 108018 | 354 | 727 | 1081 | 18 | 1099 | 99.0 % |
| a,a,a,a,b,b,b | 143284 | 1188 | 5346 | 6534 | 18 | 6552 | 95.4 % |
| a,a,a,a,a,b,c | 160917 | 354 | 1156 | 1510 | 22 | 1532 | 99.0 % |
| a,a,a,a,b,b,c | 319614 | 1221 | 13567 | 14788 | 20 | 14808 | 95.4 % |
| a,a,a,a,b,c,d | 584109 | 1251 | 26847 | 28098 | 25 | 28123 | 95.2 % |
| a,a,a,b,c,d,e | 2171079 | 4324 | 486158 | 490482 | 28 | 490510 | 77.4 % |
| a,a,b,c,d,e,f | 6402999 | 11053 | 4218898 | 4229951 | 32 | 4229983 | 33.9 % |
| a,b,c,d,e,f,g | 12750879 | 17319 | 12733560 | 12750879 | 28 | 12750907 | 0.0 % |
Se observa una reducción muy significativa. El coste de ordenar es insignificante con respecto al resto. A medida que la muestra contiene más elementos distintos la reducción es menor, de tal forma que con todos los elementos distintos se reduce a cero y el coste es el de permuteR1 más el de ordenar.
Dificultad para encontrar la recurrencia asociada y un término general
En los temas anteriores he podido deducir un término general del coste de cada algoritmo. Para ello fue necesario contar previamente con una definición de la recurrencia. Sin embargo en este caso ni siquiera he conseguido esta definición. En el tema anterior pudimos definirla así:
| T(n) = | { | m+1 | si n≤1 |
| n T(n-1) + n + 1 | si n> 1 |
En esa definición m tenía que ver con el coste de la función auxiliar includesArray(). Además de eso ahora el problema es que tenemos un condicional dentro de la recurrencia, reduciendo el número de llamadas. Antes se produción n llamadas a T(n-1) y ahora se producen esas o menos. Pero cuántas menos no queda claro.
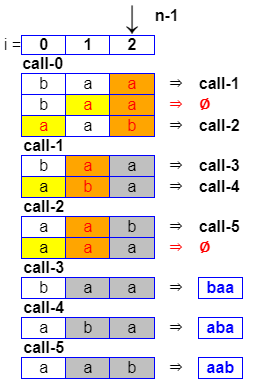
En la Figura podemos ver un esquema de la evolución del algoritmo para el simple ejemplo con una lista inicial con sólo tres términos { b, a, a }. Cada llamada itera por el número de elementos, inicialmente tres. Se itera desde la derecha del Array, en la columna con color naranja que hace las veces de pivote, comparando ese valor con el resto. Cuando es el inicial o son diferentes produce una nueva llamada. Vemos que en la segunda fila se comparan iguales y no produce llamada. Al final vemos en color azul las permutaciones con repetición que se generan { {b,a,a}, {a,b,a}, {a,a,b} }.
Vemos que, aparte de la llamada inicial, se producen cinco llamadas de siete posibles. Y esto se puede complicar más para los múltiples casos distintos de listas inciales. En este caso hay dos letras que se repiten y una que no. Pero la forma de combinar repeticiones complica la búsqueda de una definición del problema, algo que por ahora no he conseguido.
Mejora generando multinomiales usando Set() de JavaScript
Una última mejora que podemos hacer con el algoritmo anterior es usar el objeto Set() de JavaScript. Si lo que generamos es un conjunto de permutaciones con repetición, la estructura Set() es la adecuada, pues se agregará un nuevo elemento con su método add() si no existe previamente. Con esto evitamos usar la función auxiliar includesArray() del algoritmo anterior:
function permuteR3(list=[]){
function permuteSet(list=[], n=list.length, res=new Set()) {
if (n<=1) {
//iter += list.length;
res.add(list.join(","));
} else {
//iter += 1;
for (let j=n-1; j>-1; j--){
//iter += 1;
if (j===n-1 || list[j]!==list[n-1]) {
[list[j], list[n-1]] = [list[n-1], list[j]];
permuteSet(list, n-1, res);
[list[j], list[n-1]] = [list[n-1], list[j]];
}
}
}
return res;
}
let result = [...permuteSet(list)];
//iter += result.length;
result = result.map(v => v.split(","));
//iter += result.length*list.length;
return result;
}Almacenamos los resultados parciales como String usando el método list.join(","), pues Set necesitará compararar valores, no objetos. Esto tiene un coste de la longitud del resultado parcial list.length. En lo anterior estamos considerando que el coste de agregar un elemento con add() es unitario, que en serie con list.length tomaremos el máximo que es este último.
Cuando obtengamos todas las permutaciones hemos de convertir Set en un Array, a la vez que deshacemos list.join(","). Aún con estos costes adicionales se observa en la siguiente tabla con algunas muestras como se reducen significativamente los tiempos de ejecución. Las muestras tienen la estructura de 2 letras repetidas y el resto distintas, con lo que la fórmula de la permutaciones con repetición es p = n! / (2!×1!×···×1!).
| n | p | Muestra | permuteR1 | permuteR2 | permuteR3 | |||
|---|---|---|---|---|---|---|---|---|
| Iter | ms | Iter | ms | Iter(*) | ms | |||
| 6 | 360 | a,a,b,c,d,e | 136393 | 4 | 83526 | 3 | 6100 | 1 |
| 7 | 2520 | a,a,b,c,d,e,f | 6402999 | 65 | 4229951 | 46 | 49621 | 7 |
| 8 | 20160 | a,a,b,c,d,e,f,g | >2×107 | - | >2×107 | - | 454242 | 29 |
| 9 | 181440 | a,a,b,c,d,e,f,g,h | >2×107 | - | >2×107 | - | 4613071 | 212 |
| 10 | 1814400 | a,a,b,c,d,e,f,g,h,i | >2×107 | - | >2×107 | - | >2×107 | - |
Además observamos que puede ejecutar muestras de tamaño 8 y 9 sin superar el máximo de 20 millones de iteraciones que hemos impuesto en la aplicación. Por supuesto que no podemos considerar que el coste de add() sea unitario, pero en cualquier caso es bastante inferior a usar includesArray() del algoritmo anterior. Si observamos la segunda fila vemos que el factor de reducción de tiempos está entre 65/7 = 9.3 y 46/7 = 6.6, con lo que podríamos considerar un factor próximo a un promedio de 8, así que los valores de la columna de las iteraciones de permuteR3 marcados con (*) se podrían multiplicar por 8, estimándose iteraciones que seguirián siendo inferiores a los otros dos algoritmos.
Con n = 11 el número de permutaciones con repetición es p = 19958400 ≈ 1.996×107. Antes de superar el límite de 2×107 iteraciones que hemos impuesto en la aplicación obtenemos el error de JavaScript Set maximum size exceeded. En la página de Stackoverflow sobre el límite de tamaño para un objeto Set de JavaScript he visto un test, que también he comprobado con Chrome-Windows que el máximo está en 224 = 16777216 ≈ 1.68×107, valor inferior al que necesitamos para n = 11.