Desarreglos parciales recursivo
Desarreglos parciales: Otra forma de calcular el valor numérico
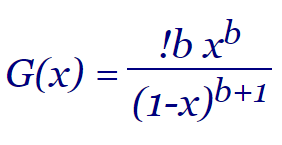
En el tema anterior vimos que los desarreglos parciales de una lista con n elementos distintos son todas las sublistas ordenadas con n elementos distintos que se pueden generar de tal forma que solo k elementos aparecen en su posición original. También se pueden definir como las permutaciones de n elementos con k puntos fijos. Las denotamos como D(n, k), correspondiendo con k=0 a los desarreglos sin puntos fijos que vimos en un tema anterior.
En ese tema anterior vimos que el número de desarreglos parciales se calcula con la siguiente fórmula, donde D(n-k, 0) = !(n-k)
Haciendo uso de la recurrencia del Triángulo de Pascal
Sustituyendo en [1]
| = D(n-1, k-1) + | C(n-1, k) | C(n, k) D(n-k, 0) = |
| C(n, k) |
| = D(n-1, k-1) + (1- | k | ) C(n, k) D(n-k, 0) = |
| n |
| = D(n-1, k-1) + C(n, k) D(n-k, 0) - | k | C(n, k) D(n-k, 0) = |
| n |
| = D(n-1, k-1) + D(n, k) - | k | D(n, k) |
| n |
En [2] vemos que C(n-1, k) / C(n, k) = 1-k/n pues
| = | C(n-1, k) | = | (n-1)! | = |
| k! (n-1-k)! | ||||
| C(n, k) | n! | |||
| k! (n-k)! |
| = | (n-1)! k! (n-k)! | = | n-k | = 1 - | k |
| k! (n-1-k)! n! | n | n |
Volviendo a [3] nos queda
| D(n, k) = D(n-1, k-1) + D(n, k) - | k | D(n, k) |
| n |
Despejando queda esta otra fórmula recurrente para obtener el número de desarreglos parciales:
| D(n, k) = | n | D(n-1, k-1) |
| k |
Como n≥k, el caso base está en k=0 en cuyo momento n será n-k = n, obteniéndose el valor base D(n-k, 0) = !(n-k) = !n
En el tema anterior obtuvimos los primeros valores para la fórmula [1]
| n | D(n, k) = C(n, k) D(n-k, 0) | ||||||
|---|---|---|---|---|---|---|---|
| k=0 | k=1 | k=2 | k=3 | k=4 | k=5 | k=6 | |
| 0 | 1 | ||||||
| 1 | 0 | 1 | |||||
| 2 | 1 | 0 | 1 | ||||
| 3 | 2 | 3 | 0 | 1 | |||
| 4 | 9 | 8 | 6 | 0 | 1 | ||
| 5 | 44 | 45 | 20 | 10 | 0 | 1 | |
| 6 | 265 | 264 | 135 | 40 | 15 | 0 | 1 |
Si aplicamos [4] a la tabla anterior obtenemos los mismos valores para n≥1, k≥1
| n | D(n, k) = n/k D(n-1, k-1) | |||||
|---|---|---|---|---|---|---|
| k=1 | k=2 | k=3 | k=4 | k=5 | k=6 | |
| 1 | 1/1×D(0,0)=1 | |||||
| 2 | 2/1×D(1,0)=0 | 2/2×D(1,1)=1 | ||||
| 3 | 3/1×D(2,0)=3 | 3/2×D(2,1)=0 | 3/3×D(2,2)=1 | |||
| 4 | 4/1×D(3,0)=8 | 4/2×D(3,1)=6 | 4/3×D(3,2)=0 | 4/4×D(3,3)=1 | ||
| 5 | 5/1×D(4,0)=45 | 5/2×D(4,1)=20 | 5/3×D(4,2)=10 | 5/4×D(4,3)=0 | 5/5×D(4,4)=1 | |
| 6 | 6/1×D(5,0)=264 | 6/2×D(5,1)=135 | 6/3×D(5,2)=40 | 6/4×D(5,3)=15 | 6/5×D(5,4)=0 | 6/6×D(5,5)=1 |
Desplegando la recurrencia
Desplegamos la recurrencia [4]
| D(n, k) = | n | D(n-1, k-1) = |
| k |
| = | n | ( | n-1 | D(n-2, k-2) ) = | n(n-1) | D(n-2, k-2) = |
| k | k-1 | k(k-1) |
| = | n(n-1) | ( | n-2 | D(n-3, k-3) )= | n(n-1)(n-2) | D(n-3, k-3) = |
| k(k-1) | k-2 | k(k-1)(k-2) |
| = | n(n-1)(n-2)···(n-(k-1)) | D(n-k, k-k) = |
| k(k-1)(k-2)···1 |
| = | nk | D(n-k, 0) = | n! | !(n-k) | = C(n, k) !(n-k) |
| k! | k! (n-k)! |
Hemos obtenido la solución esperada D(n, k) = C(n, k) !(n-k) tras haber identificado el factorial descendente
| n(n-1)(n-2)···(n-k+1) = nk = | n! |
| (n-k)! |
Resolviendo la recurrencia con secuencia de primeros casos
Vamos a solucionar la recurrencia
| D(n, k) = { | !(n-k) | si k=0 |
| n/k D(n-1, k-1) | si k>0 |
Como vimos en caso base genérico, suponiendo que los valores iniciales son n0, k0, esta recurrencia se desplaza también en k con los valores k0, k0-1, k0-2,..., 2, 1, 0 y en n con los valores n0, n0-1, n0-2,..., n0-(k0-1), n0-k0
Si designamos b=n0-k0 vemos que esta diferencia permanece constante pues
Entonces para todo n,k tenemos que b=n-k es constante, pudiéndose modificar la recurrencia con una sola variable, teniendo en cuenta que b=n-k ⇒ k = n-b
| D(n) = { | !b | si n-b=0 |
| n/(n-b) D(n-1) | si n-b>0 |
que es lo mismo que
| D(n) = { | !b | si n=b |
| n/(n-b) D(n-1) | si n>b |
De forma compacta
En un tema anterior también vimos como resolver recurrencias con caso base genérico, mostrando que una forma de resolverlo es obteniendo una secuencia de primeros casos base para ver si deducimos un término general:
En lo anterior hemos usado Wolfram Alpha para resolver las recurrencias y obtener el término general y la función generadora, como por ejemplo para el último caso. Por otro lado tomamos los valores del subfactorial !b = 1, 0, 1, 2, 9, 44, ..., valores que se replican en las funciones generadoras, por lo que podemos suponer la general así:
| G(x) = | !b xb |
| (1-x)b+1 |
Para suponer el término general observamos primero el factorial descendente que ya vimos en [5] y que suponemos que esta parte se generaliza así
| n(n-1)(n-2)···(n-(b-1)) = nb = | n! |
| (n-b)! |
Observamos ahora que la secuencia 1, 0, 1/2, 1/3, 3/9, 11/30, ... es el resultado de diviir la secuencia del subfactorial !b = 1, 0, 1, 2, 9, 44, ... entre la del factorial b! = 1, 1, 2, 6, 24, 120, ... pues
Por lo tanto el término general suponemos que es así:
| D(n) = | !b n! | = !b C(n, b) |
| b! (n-b)! |
Entonces
| G(x) = | !b xb | = ∑n≥b !b C(n, b) xn |
| (1-x)b |
Si deshacemos el cambio b=n-k observamos que C(n, b) = C(n, k)
| D(n, k) = | !(n-k) n! | = !(n-k) | n! | = C(n, k) !(n-k) |
| (n-k)! (n-(n-k))! | k! (n-k)! |
Obteniendo la solución general esperada
Resolviendo la recurrencia con función generadora
Resolvemos la misma recurrencia aplicando la técnica de la función generadora
| D(n) = { | !b | si n=b |
| n/(n-b) D(n-1) | si n>b |
De forma compacta
Incrementamos índices
Usaremos esta función generadora
Estas son las condiciones iniciales
Aplicando la función generadora a la recurrencia
| ∑n≥b D(n+1) xn | = ∑n≥b | n+1 | D(n) xn |
| n-b+1 |
Veamos la parte izquierda de [12]
| = | 1 | ∑n≥b D(n+1) xn+1 | = | 1 | ∑n≥b+1 D(n) xn | = |
| x | x |
| = | 1 | ( - Gb(x) + ∑n≥b D(n) xn ) = |
| x |
| = | 1 | ( - !b xb + G(x) ) = - !b xb-1 + | G(x) |
| x | x |
Veamos la parte derecha de [12]
| ∑n≥b | n+1 | D(n) xn | = ∑n≥b ( | b | + 1 ) D(n) xn | = |
| n-b+1 | n-b+1 |
| = b ∑n≥b | 1 | D(n) xn | + ∑n≥b D(n) xn = |
| n-b+1 |
| = b ∑n≥b | D(n) | xn | + G(x) |
| n-b+1 |
Veamos la serie en [14]
| ∑n≥b | D(n) | xn | =∑n≥1 | D(n+b-1) | xn+b-1 | = |
| n-b+1 | n |
| = xb-1 ∑n≥1 | D(n+b-1) | xn |
| n |
Para seguir resolviendo primero vemos que:
Ahora supongamos lo siguiente:
- a(n) = D(n+b)
- a(n-1) = D(n+b-1)
- ∑n≥1 (an-1 / n) xn = ∑n≥1 (D(n+b-1)/n) xn que es el sumatorio en [15]
- A(x) = ∑n≥0 D(n+b) xn = G(x)/xb tal como vimos antes
- ∫ A(x) dx = ∑n≥1 (an-1 / n) xn por el principio de integrales de una serie que ya hemos visto en un tema anterior
Por lo tanto la serie en [15] queda así:
| ∑n≥1 | D(n+b-1) | xn = ∫ | G(x) | dx |
| n | xb |
Actualizando [14] con [15] y [16] y agrupando con [13] en [12] nos queda:
| - !b xb-1 + | G(x) | = b xb-1 ∫ | G(x) | dx + G(x) |
| x | xb |
Reagrupando G(x)
| - !b xb-1 + G(x) | 1-x | = b xb-1 ∫ | G(x) | dx |
| x | xb |
Dejando solo la integral en la parte derecha
| - | !b | + G(x) | 1-x | = ∫ | G(x) | dx |
| b | b xb | xb |
Derivando en ambos lados
| G'(x) | 1-x | + G(x) | d | ( | 1-x | ) = | G(x) |
| b xb | dx | b xb | xb |
quedando
| G'(x) | 1-x | + G(x) ( | bx-b-x | ) = | G(x) |
| b xb | b xb+1 | xb |
Tras simplificaciones que puede ver en el desplegable siguiente, queda finalmente la siguiente ecuación diferencial lineal ordinaria con coeficientes variables de primer orden, homogénea en este caso:
| G'(x) | = | (x+b) |
| G(x) | x (1-x) |
Se resuelve integrando en ambos lados:
| ∫ | G'(x) | dx = ∫ | (x+b) | dx |
| G(x) | x (1-x) |
Resultando:
Tras manipular los logaritmos y la constante, exponenciamos en ambos lados para obtener finalmente la función generadora:
| G(x) = | c xb |
| (1-x)b+1 |
Obteniendo la solución general
Lo que acabamos de obtener en el apartado anterior es como [6] a excepción de la constante c = !b que hemos de validar tras obtener el término general de la función generadora genérica sin la constante:
| G(x) = | xb |
| (1-x)b+1 |
Cuando tenemos una función generadora y queremos buscar la solución o término general podemos hacer uso del Desarrollo de Taylor. Pero esta función tiene el problema de que hay que valorar en x=0 y ahí la función y sus derivadas iniciales valen cero, pues:
| G0(0) = | 0b | =0 |
| (1-0)b+1 |
Las primeras derivadas son:
| G1(x) = | b xb-1 + xb |
| (1-x)b+2 |
| G2(x) = | b(b-1) xb-2 + 4 b xb-1 + 2 xb |
| (1-x)b+3 |
| G3(x) = | b(b-1)(b-2) xb-3 + 9 b(b-1) xb-2 + 18 b xb-1 + 6 xb |
| (1-x)b+4 |
Se observa que para las derivadas G0(0) hasta Gb-1(0) resultarán cero y sólo a partir de la derivada Gb(0) = b(b-1)(b-2)···3·2·1 para ver la primera distinta de cero. Por lo tanto no parece fácil usar esta técnica a menos que hagamos lo siguiente:
| G(x) = | xb | = xb | 1 | = xb f(x) |
| (1-x)b+1 | (1-x)b+1 |
Y trataremos de obtener el desarrollo de Taylor de f(x), tal como hicimos en un tema anterior cuando tratamos los casos base genéricos:
| f(x) = | 1 | ⇒ f 0(0) = 1 |
| (1-x)b+1 |
| f 1(x) = | b+1 | ⇒ f 1(0) = b+1 |
| (1-x)b+2 |
| f 2(x) = | (b+1)(b+2) | ⇒ f 2(0) = (b+1)(b+2) |
| (1-x)b+3 |
| f 3(x) = | (b+1)(b+2)(b+3) | ⇒ f 3(0) = (b+1)(b+2)(b+3) |
| (1-x)b+4 |
Parece que no es necesario seguir pues se supone el término general para n≥1
| f n(x) = | (b+1)(b+2)···(b+n) | ⇒ f n(0) = (b+1)(b+2)···(b+n) |
| (1-x)b+n+1 |
Como pochhammer genera la secuencia para n≥0 siguiente
Entonces podemos generalizar para n≥0
Entonces
| f(x) = | 1 | = ∑n≥0 (b+1)n | xn |
| (1-x)b+1 | n! |
Y nuestra función es
| G(x) = xb f(x) = | xb | = ∑n≥0 (b+1)n | xn+b | = |
| (1-x)b+1 | n! |
| = ∑n≥b | (b+1)n-b | xn |
| (n-b)! |
Como vimos en pochammer que nk = k! C(n+k-1, k) entonces el término general queda así:
| (b+1)n-b | = | (n-b)! C(b+1+n-b-1, n-b) | = C(n, n-b) = C(n, b) |
| (n-b)! | (n-b)! |
Se observa que hemos aplicado C(n, n-b) = n!/((n-b)! b!) = C(n, b) con lo que hemos alcanzado lo mismo que obtuvimos en [8] a falta de la constante c que aún hemos de determinar en [17]:
| G(x) = c | xb | = c ∑n≥b C(n, b) xn |
| (1-x)b |
Resolviendo la constante
Para resolver la constante volvemos a recordar la recurrencia:
| D(n) = { | !b | si n=b |
| n/(n-b) D(n-1) | si n>b |
Y el caso base junto a [11] que se obtenía de la definición de esa recurrencia:
Entonces y, como era de esperar, tras ver que C(b, b) =1 obtenemos c = !b
Con lo que obtenemos la misma solución con la técnica de la función generadora que con las otras dos usando el despliegue o una secuencia de primeros casos base:
| G(x) = | !b xb | = ∑n≥b !b C(n, b) xn |
| (1-x)b |