Permutaciones con repetición o Multinomiales
Las permutaciones con repetición o multinomiales
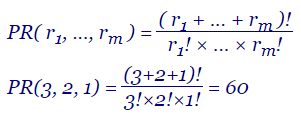
Las permutaciones con repetición, también denominado multinomial, de un conjunto de una lista A = { a1, ..., an } donde pueden producirse repeticiones y al quitar los elementos repetidos obtenemos otra lista { b1, ..., bm } con m≤n elementos distintos, donde cada elemento bi puede estar repetido ri veces, con 0 ≤ ri ≤ n, de tal forma que r1+...+rm = n, son todas las posibles ordenaciones de la lista A. Se denota como PR(r1, ..., rm).
Se obtiene el valor numérico con la siguiente fórmula:
| PR( r1, ..., rm ) = | ( r1 + ... + rm )! |
| r1! × ... × rm! |
Si el conjunto de entrada es {a, a, a, b, b, c}, el resultado será el siguiente, donde se observa que "a" se repite tres veces, "b" dos veces y "c" una vez:
| PR(3, 2, 1) = | (3+2+1)! | = 60 |
| 3!×2!×1! |
Se observa que el número de elementos del conjunto anterior es n = 6, cumpliéndose que r1 + ... + rm = 3+2+1 = 6 y que 6! = 720, que dividido entre 3!×2!×1! = 6×2×1 = 12 resultan los 60 obtenidos. El caso cuando se produce una única repetición de cada elemento, teniendo en el denominador 1!×1!×···×1! = 1, resulta en las permutaciones normales, es decir:
| PR(1, ··n··, 1) = | (1+··n··+1)! | = | n! | = n! = P(n) |
| 1!×··n··×1! | 1 |
El algoritmo permuteR1({a0, a1, ...}) genera las permutaciones con repetición (o multinomiales) del conjunto que se le pase, aunque hay que pasarlo como un Array. Por ejemplo con el conjunto anterior:
permuteR1(["a", "a", "a", "b", "b", "c"])se obtiene una Array de 60 términos, con cada uno de ellos siendo a su vez un Array. El primero es ["a", "a", "a", "b", "b", "c"] una copia de la entrada. Con la opción de la herramienta Combine Tools podemos presentar los resultados de forma compacta así:
aaabbc aababc abaabc baaabc aabbac ababac baabac abbaac babaac bbaaac aaabcb aabacb abaacb baaacb aaacbb aacabb acaabb caaabb aacbab acabab caabab aabcab abacab baacab abcaab bacaab acbaab cabaab cbaaab bcaaab aacbba acabba caabba aabcba abacba baacba abcaba bacaba acbaba cababa cbaaba bcaaba aabbca ababca baabca abbaca babaca bbaaca abcbaa bacbaa acbbaa cabbaa cbabaa bcabaa abbcaa babcaa bbacaa bbcaaa bcbaaa cbbaaaAclarando términos permutaciones con repetición y multinomial
Como ya hemos dicho muchas veces en temas anteriores, en esta serie de temas y en la utilidad Combine Tools diferenciamos entre permutaciones y variaciones, pues en mucha documentación sólo hablan de k-permutaciones P(n, k) ignorando las variaciones. Ambas se equiparan con P(n, k) = V(n, k) y P(n, n) = V(n, n) = n! En estos temas sólo se contempla P(n) para las permutaciones y PR( r1, ..., rm ) para las permutaciones con repetición. Mientras que, como veremos en siguientes temas, las variaciones son V(n, k) y las variaciones con repetición VR(n, k).
Debido a eso en dichos otros documentos las permutaciones con repetición es PR(n, k) = nk, algo distinto a lo que estamos viendo en este tema, pues para nosotros esas serían las variaciones con repetición. Por eso podemos ver escrito las permutaciones con repetición de este tema como multinomial, o más específicamente como coeficientes multinomiales. Con este ejemplo podrá acceder a la ejecución en Wolfram Alpha, que usa la función multinomial() en lenguaje natural. Recuerde que ese enlace también está disponible usando el recurso Copy Math:
A las combinaciones sin repetición se les denomina también binomiales, pues se obtienen los coeficientes binomiales del desarrollo de Newton en dos variables (x+y)n. Las permutaciones con repetición también se les denomina multinomiales, pues se obtienen los coeficientes multinomiales en múltiples variables, desarrollando (x+y+z+...)n. En el último apartado veremos más sobre esto.
Dada la similitud entre ambos conceptos, a veces se representan las permutaciones con repetición de forma parecida a las combinaciones, donde cabían estas representaciones ampliamente reconocidas:
Así para las permutaciones con repetición o multinomiales podemos encontrar:
En las dos últimas n podría sobrar, pues la suma de r1+ ...+ rm = n obligatoriamente. La forma PR() no es ampliamente conocida, dado que no suele usarse la denominación permutaciones con repetición sino multinomiales.
Primera implementación de un algoritmo para construir las permutaciones con repetición (o multinomiales)
Para una primera implementación de un algoritmo que genere las permutaciones con repetición podemos partir de las permutaciones normales. Por ejemplo, las permutaciones del conjunto A = { a, b, c } son PA = { abc, acb, bac, bca, cab, cba }. Si en cambio el conjunto de partida es A = { a, a, c } donde se repite la "a", el resultado es el mismo sustituyendo "b" por "a", es decir PA = { aac, aca, aac, cca, caa, caa }. Obviamente como debe ser un conjunto no puede haber elementos repetidos, así que las permutaciones con repetición debe ser PRA = { aac, aca, cca }.
En las permutaciones normales no se permiten (o no deberían permitirse) elementos repetidos. Pero esto no quita para que podamos usar algunos de los algoritmos que las generan, como el algoritmo de Heap que vimos en el tema anterior. Este sería el algoritmo planteado:
// Heap algorithm to generate permutations with repetition (multinomial)
function permuteR1(list=[], n=list.length, result=[]){
if (n<=1) {
//iter += 1;
if (!includesArray(result, list)) {
//if (withCopyCost) iter += list.length;
result.push(copy(list));
}
} else {
//iter += 1;
for (let j=n-1; j>-1; j--){
//iter += 1;
[list[j], list[n-1]] = [list[n-1], list[j]];
permuteR1(list, n-1, result);
[list[j], list[n-1]] = [list[n-1], list[j]];
}
}
return result;
}Necesitaremos además la función auxiliar includesArray() para comprobar si ya tenemos un resultado parcial almacenado en los resultados:
// Implement Array.includes() function to count iterations.
function includesArray(result=[], list=[]){
let included = false;
//iter += list.length;
let listString = list.join(",");
if (!Array.isArray(result.value)) result.value = [];
for (let i=0; i<result.value.length; i++){
//iter += 1;
if (result.value[i]===listString){
included = true;
break;
}
}
if (!included) result.value.push(listString);
return included;
}El algoritmo es igual al visto en Heap en la parte del condicional n>1. La diferencia está en el caso base, donde antes de guardar cada resultado parcial en result comprobamos si ya existe en result.value. Cada resultado parcial es un Array. Por ejemplo ["a", "a", "c"]. En result.value los vamos almacenando como un String "a,a,c", con objeto de ir comprobando si ya existe previamente en cuyo caso lo descartaremos.
Hay que entender que es mejor usar el método includes() o indexOf() de Array, pues serán más eficientes. Pero no es posible de forma directa comprobar si un elemento Array está incluido en otro Array usando este método, pues sólo comprueba tipos primitivos (number, string, boolean, symbol, null, undefined). Por ejemplo, probando
[[1, 2], [3, 4]].includes([1, 2])en la consola del navegador observará que se obtiene falso. Sin embargo con
["1,2", "3,4"].includes("1,2")se obtiene verdadero. Si queremos comprobar la existencia de tipos no primitivos podríamos usar el método findIndex() de Array, pasando un callBack con el Array que queremos buscar pasado en el argumento thisArg. Puede probar este código en la consola:
function callBack(v) {
return v.join(",")===this.w.join(",")
}
[[1, 2], [3, 4], [5, 6]].findIndex(callBack, {w: [3, 4]});
// Se obtiene la posición 1, si no lo encuentra se obtiene -1En cualquier caso aquí vamos a analizar el coste tomando la función auxiliar dada includesArray(), pues nos permite incluir las sentencias con iter que cuentan las iteraciones. Aparecen comentadas en el código, pero en la ejecución se incluyen para llevar a cabo ese contaje de iteraciones.
Analizando el coste de permuteR1()
Analicemos el coste (por ahora sin coste de copia) del algoritmo permuteR1() con esta definición de la recurrencia:
| T(n) = | { | m+1 | si n≤1 |
| n T(n-1) + n + 1 | si n> 1 |
Con n>1 la definición es la misma que la que vimos para el algoritmo permute3() que resolvíamos aplicando el Algoritmo de Heap: T(n) = n T(n-1) + n + 1. Para n≤1 el coste entonces era T(n) = 1. Pero ahora le vamos a dar el valor T(n) = m+1, de tal forma que cuando m=0 estamos en el caso de permutaciones de Heap. El objetivo de la variable m es tener en cuenta el coste de la función auxiliar includesArray().
Partiendo de la definición y aplicando la técnica de la función generadora exponencial llegamos al siguiente término general, igual que el visto en el tema anterior para el caso m=0:
| T(n) = - m n! + 2 n! - 1 + 2 ∑j=2..n | n! |
| j! |
En el desplegable siguiente puede observar el proceso de obtención, que es similar al visto en el tema anterior.
Para ver cuál es el termino de m partimos de la fórmula [1] que vimos para obtener el valor númerico de las permutaciones con repetición, que también podemos expresar así, puesto que ∑j=1..m rj = n:
| p = | n! |
| ∏j=1..m rj! |
Con este valor de p la fórmula que involucra m es:
| -m n! = | n! | ∑j=0..p-1 (j+1) - p + n n! |
| p |
Trataremos de explicar como se obtuvo esa expresión en el siguiente apartado. Podemos resolver la suma anterior para expresarlo de una forma compacta (Wolfram Alpha):
| -m n! = | 1 | (p+1) n! - p + n n! |
| 2 |
Esta fórmula es lo que aporta la función includesArray() al algoritmo de Heap, incrementando su coste como veremos en el siguiente apartado. Es fruto de la observación de ese algoritmo y de pruebas experimentales, como explicaremos en un siguiente apartado.
Despejando la m obtenemos:
| m = - | 1 | (p+1) + | p | - n n! |
| 2 | n! |
Para nuestro algoritmo de Heap, que siempre usará la función auxiliar includesArray(), esta expresión dará valores negativos como se observa en Wolfram Alpha para el caso p = n!, con lo que el componente -m n! resultará positivo, incrementando el coste del algoritmo de Heap.
Finalizamos sustituyendo el valor -m n! del componente [5] en [2] llegando a la solución final siguiente:
| T(n) = | 1 | (p+1) n! - p + n n! + 2n! - 1 + 2 ∑j=2..n | n! |
| 2 | j! |
Aplicamos una simplificación para obtener una sola aparición de la variable p:
| T(n) = | n!-2 | p + | 2n+1 | n! + 2n! - 1 + 2 ∑j=2..n | n! |
| 2 | 2 | j! |
Los tres últimos términos son el coste del algoritmo de Heap que vimos en el tema anterior, coste que se incrementa de forma significativa con los dos primeros términos. Podríamos definir la expresión como T(n) = TM(n) + TH(n) de tal forma que:
| TM(n) = | n!-2 | p + | 2n+1 | n! |
| 2 | 2 |
| TH(n) = 2n! - 1 + 2 ∑j=2..n | n! |
| j! |
Coste de la función para incluir un resultado parcial
En el apartado anterior usábamos la función auxiliar includesArray() que volvemos a repetir aquí:
// Implement Array.includes() function to count iterations.
function includesArray(result=[], list=[]){
let included = false;
//iter += list.length;
let listString = list.join(",");
if (!Array.isArray(result.value)) result.value = [];
for (let i=0; i<result.value.length; i++){
//iter += 1;
if (result.value[i]===listString){
included = true;
break;
}
}
if (!included) result.value.push(listString);
return included;
}Expusimos sin demostrarlo que el coste de esta función era lo visto en las expresiones equivalentes [4], [5] y [8]:
| TM(n) = | n! | ∑j=0..p-1 (j+1) - p + n n! = |
| p |
| = | 1 | (p+1) n! - p + n n! = |
| 2 |
| = | n!-2 | p + | 2n+1 | n! |
| 2 | 2 |
Usaremos la primera de las tres expresiones para intentar explicarlo a partir del uso de la función para buscar si un resultado parcial ya existe en el resultado final. Partimos de las permutaciones con repetición de un conjunto sin repeticiones, como A = { a, b, c } cuyo valor numérico es PR(1, 1, 1) = 3! = 6 puesto que obedece a la fórmula que vimos en [1]:
| PR(1, 1, 1) = | (1+1+1)! | = 3! = 6 |
| 1!×1!×1! |
Son en este caso las permutaciones normales del conjunto de partida cuyo valor numérico es 3! = 6. A la función buscar llegan los resultados parciales en list, de tal forma que cada uno de ellos no existirá previamente en el Array result, finalizando con este proceso acumulativo:
| call | list | result | includesArray (result, list) | list.length + i |
|---|---|---|---|---|
| 0 | [a,b,c] | [] | false | 3+0=3 |
| 1 | [b,a,c] | [[a,b,c]] | false | 3+1=4 |
| 2 | [a,c,b] | [[a,b,c], [b,a,c]] | false | 3+2=5 |
| 3 | [c,a,b] | [[a,b,c], [b,a,c], [a,c,b]] | false | 3+3=6 |
| 4 | [c,b,a] | [[a,b,c], [b,a,c], [a,c,b], [c,a,b]] | false | 3+4=7 |
| 5 | [b,c,a] | [[a,b,c], [b,a,c], [a,c,b], [c,a,b], [c,b,a]] | false | 3+5=8 |
El número de iteraciones finales en la función para este caso es el siguiente, donde se observa que en cada ejecución de la función hay que sumar 3 que es el coste de convertir en String el resultado parcial con let listString = list.join(","):
Si comprobamos en la aplicación Combine Tools el valor de permute3(["a", "b", "c"]) para las permutaciones de Heap de ese conjunto, obtendremos el valor de coste TH(3) = 19. Entonces el coste total será de T(3) = TM(3) + TH(3) = 33 + 19 = 52, valor que es conforme con el que obtendríamos con el algoritmo permuteR3(["a", "b", "c"]).
Es obvio llegar a esta conclusión:
De donde tenemos una primera expresión general para el caso de conjuntos sin repeticiones:
Podemos generalizar lo anterior viendo que para el caso de un conjunto sin repeticiones { a, b, c, ... } tenemos que n! = p puesto que las permutaciones con repetición en este caso son p = n! / (1!×1!× ··· ×1!×1!). Con esto lo anterior también podemos expresarlo así, aún para el caso de conjuntos sin repeticiones:
Tenemos algo muy parecido a lo que vemos en [10]. Como sin repetición p = n! y viendo que p = ∑j=0..p-1 1 podemos manipular lo anterior:
| = | n! | ∑j=0..p-1 j + n n! = |
| p |
| = | n! | ( ∑j=0..p-1 j ) + ( ∑j=0..p-1 1 ) - p + n n! = |
| p |
| = | n! | ∑j=0..p-1 (j+1) - p + n n! |
| p |
Esta expresión, que es igual que [10], es válida para conjuntos sin repetición como A = { a, b, c }. Pero resulta que también lo es para conjuntos con repetición.Y no es fácil ver lo que pasa para los casos con repeticiones, que pueden ser muy diferentes. Veamos el caso más simple cuando A = { a, a, c }, cuyas permutaciones con repetición producen los resultados { {a,a,c}, {a,c,a}, {c,a,a} }. La evolución en la función buscar es la siguiente:
| call | list | result | includesArray (result, list) | list.length + i |
|---|---|---|---|---|
| 0 | [a,a,c] | [] | false | 3+0=3 |
| 1 | [a,a,c] | [[a,a,c]] | true | 3+1=4 |
| 2 | [a,c,a] | [[a,a,c]] | false | 3+1=4 |
| 3 | [c,a,a] | [[a,a,c], [a,c,a]] | false | 3+2=5 |
| 4 | [c,a,a] | [[a,a,c], [a,c,a], [c,a,a]] | true | 3+3=6 |
| 5 | [a,c,a] | [[a,a,c], [a,c,a], [c,a,a]] | true | 3+2=5 |
Se observa ahora que en algunos casos el resultado parcial ya existe y en otros no. Sumando las iteraciones de la tabla anterior y, por otro lado, calculando el valor de TH(3) usando Combine Tools para las permutaciones de Heap para un conjunto de 3 elementos sin repeticiones tenemos:
Y este valor es el resultado correcto del coste de obtención de las permutaciones con repetición para el conjunto A = { a, a, c }. Usando la fórmula [10] llegaremos al mismo valor TM(3) = 27, viendo que p = 3!/(2!×1!) = 3
| TM(3) = | 3! | ∑j=0..3-1 (j+1) - 3 + 3×3! = 27 |
| 3 |
La verdad es que no he podido demostrar matemáticamente que [10] es cierto para todos los casos con repetición. En el apartado siguiente probaremos valores tratando de estructurar los distintos conjuntos con repetición, algo que puede confirmarnos experimentalmente que podríamos estar en lo cierto.
Estructurando los distintos conjuntos con repetición
Los algoritmos que hemos visto en temas anteriores tienen una clara estructura de ejecución, con una lista de elementos necesariamente distintos sobre los que generamos un conjunto de sublistas. Por ejemplo, con combine({a,b,c}, 2) generamos las combinaciones de 3 elementos distintos tomados en subconjuntos de 2 elementos. Con permute({a,b,c}) generamos las permutaciones de un conjunto de 3 elementos necesariamente distintos. Pero ahora con las pemutaciones con repetición o multinomiales los elementos no son necesariamente distintos.
Y esto nos obliga a estructurar los tipos de conjuntos con los que nos podemos enfrentar. Supongamos que tenemos el siguiente conjunto con n elementos iguales o distintos, donde cada elemento αi puede ser una letra a, b, c, ...
Lo estructuramos de tal forma que el subconjunto de los n-s primeros elementos son necesariamente iguales y que los restantes no son necesariamente iguales. Y que ambos subconjuntos son disjuntos, es decir, que en un subconjunto no hay elementos que se repitan en el otro:
Observe que la variable s viene a ser el número de elementos no necesariamente distintos que intervienen en el conjunto, pues en el subconjunto S2 hay s elementos no necesariamente distintos y en el subconjunto S1 hay n-s elementos necesariamente iguales.
Con esta definición podríamos construir algunos ejemplos. Si partimos de un tamaño de conjunto 7 y todos son distintos tendríamos el conjunto {a, b, c, d, e, f, g} utilizando letras como elementos. Si son todos iguales tendríamos {a, a, a, a, a, a, a}. Si, por ejemplo hay s=3 elementos en S2 que no se repiten en los n-s elementos de S1, entonces solo cabrían estos casos:
Observe que son conjuntos y por tanto no importa el orden ni las letras que se utilicen. Así da lo mismo usar { a, a, a, a, b, b, c } que { a, a, a, a, c, c, b }, pues lo que importa es que hay 4 letras repetidas y 3 letras distintas de esas 4. Y de las 3 tenemos que 2 se repiten y 1 no se repite.
Recordando la fórmula que cuenta las permutaciones con repetición que vimos en [3]
| p = | n! |
| ∏j=1..m rj! |
Podemos calcular el valor para el conjunto { a, a, a, a, b, b, b } siendo n=7:
| p = | n! |
| (n-3)! 3! |
Y para { a, a, a, a, b, b, c }
| p = | n! |
| (n-3)! 2! 1! |
Y finalmente para { a, a, a, a, b, c, d }
| p = | n! |
| (n-3)! 1! 1! 1! |
Estos ejemplos nos permiten generalizar por casos de la variable s y para cualquier valor de n, obteniendo finalmente esta expresión general, donde ∑i=1..k ri = s cumpliéndose que (n-s) + ∑i=1..k ri = (n-s) + s = n pues es condición indispensable para aplicar la fórmula que cuenta las permutaciones con repetición:
| p = | n! |
| (n-s)! r1!···rk! |
En base a esto construimos esta tabla de ejemplos para s = 0, 1, 2, 3, n elementos no necesariamente distintos siguiente para muestras con n=1 hasta n=7, con la solución que obtuvimos en apartados anteriores y que volvemos a repetir:
| T(n) = | n!-2 | p + | 2n+1 | n! + 2n! - 1 + 2 ∑j=2..n | n! |
| 2 | 2 | j! |
| s | p | Sample (n=7) | T(n) | Link | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||||
| 0 | n! / ((n-0)! 0!) = 1 | a,a,a,a,a,a,a | 2 | 10 | 42 | 200 | 1130 | 7512 | 57638 | WA |
| 1 | n! / ((n-1)! 1!) = n | a,a,a,a,a,a,b | 2 | 10 | 46 | 233 | 1366 | 9307 | 72752 | WA |
| 2 | n! / ((n-2)! 1! 1!) = n2-n | a,a,a,a,a,b,c | 5/2 | 10 | 52 | 321 | 2251 | 17923 | 160917 | WA |
| 2 | n! / ((n-2)! 2!) = (n2-n)/2 | a,a,a,a,a,b,b | 5/2 | 10 | 46 | 255 | 1661 | 12538 | 108018 | WA |
| 3 | n! / ((n-3)! 1! 1! 1!) = n3-3n2+2n | a,a,a,a,b,c,d | 5/2 | 10 | 52 | 453 | 4611 | 50233 | 584109 | WA |
| 3 | n! / ((n-3)! 2! 1!) = (n3-3n2+2n)/2 | a,a,a,a,b,b,c | 5/2 | 10 | 46 | 321 | 2841 | 28693 | 319614 | WA |
| 3 | n! / ((n-3)! 3!) = (n3-3n2+2n)/6 | a,a,a,a,b,b,b | 5/2 | 10 | 42 | 233 | 1661 | 14333 | 143284 | WA |
| n | n! / ((n-n)! 1!···n···1!) = n! | a,b,c,d,e,f,g | 2 | 10 | 52 | 453 | 8151 | 265633 | 12750879 | WA |
En la tabla anterior exponemos los valores calculados para s = 0, 1, 2, 3, n incluyéndose una muestra con 7 elementos, cuyo coste es el de la columna n=7. Se pueden comprobar los valores en el enlace a Wolfram Alpha usando la fórmula de T(n) para cada valor de p.
Los valores fraccionarios, en las celdas con fondo gris, son los calculados por esa fórmula, pero no son aplicables dado que para s≥2 tiene que haber 2 o más elementos, es decir, si s≥2 ⇒ n≥2. Vease que en otro caso para n=1 siempre tendremos el conjunto de partida A = { a } y por tanto T(1) = 2. Además sucede que para n=2 siempre resultará T(2) = 10, tanto para la posibilidad de partir del conjunto A = { a, b } como para la única alternativa A = { a, a } cuando se repiten elementos. A partir de n≥3 según como sea el conjunto se obtendrán costes distintos.
He comprobado que todos los valores enteros obtenidos en la tabla anterior con la fórmula matemática que calcula T(n) coinciden con el contaje de iteraciones en el algoritmo ejecutado en Combine Tools.
Coste con copia del algoritmo para construir permutaciones con repetición
Para el caso de coste con copia y con listas con todos los elementos distintos hacemos lo mismo que vimos para el algoritmo de Heap, sumando n n! que es el coste de la sentencia
if (withCopyCost) iter += list.lengthPues cada resultado parcial en list tiene una longitud n y como hay n! resultados parciales, hemos de sumar n n!:
| T(n) = | n!-2 | p + | 2n+1 | n! + n n! + 2n! - 1 + 2 ∑j=2..n | n! |
| 2 | 2 | j! |
Pero lo anterior no sirve para el caso de repeticiones. Si comparamos el coste sin copia T1(n) con las iteraciones que cuenta el algoritmo en Combine Tools marcando la opción de incluir coste de copiar resultados parciales, usando las muestras que vimos en el apartado anterior, tenemos el siguiente comparativo
| Muestra n=7 | T1(n) | Iter con coste copia | Diferencia |
|---|---|---|---|
| a,a,a,a,a,a,a | 57638 | 57645 | 7 = 7×1 = 7 × PR(7) |
| a,a,a,a,a,a,b | 72752 | 72801 | 49 = 7×7 = 7 × PR(6, 1) |
| a,a,a,a,a,b,b | 108018 | 108165 | 147 = 7×21 = 7 × PR(5, 2) |
| a,a,a,a,b,b,b | 143284 | 143529 | 245 = 7×35 = 7 × PR(4, 3) |
| a,a,a,a,a,b,c | 160917 | 161211 | 294 = 7×42 = 7 × PR(5, 1, 1) |
| a,a,a,a,b,b,c | 319614 | 320349 | 735 = 7×105 = 7 × PR(4, 2, 1) |
| a,a,a,a,b,c,d | 584109 | 585579 | 1470 = 7×210 = 7 × PR(4, 1, 1, 1) |
| a,b,c,d,e,f,g | 12750879 | 12786159 | 35280 = 7×7! = 7 × PR(1, 1, 1, 1, 1, 1, 1) |
Observamos que en lugar de n n! debemos usar n p siendo p las permutaciones con repetición cuyo valor se calcula con PR(), pues dado que hay p permutaciones totales y copiar esos resultados parciales supone n p:
| T(n) = | n!-2 | p + | 2n+1 | n! + n p + 2n! - 1 + 2 ∑j=2..n | n! |
| 2 | 2 | j! |
Coeficientes multinomiales
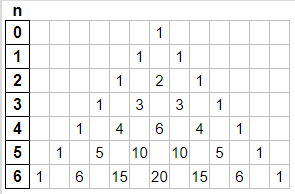
En el tema combinaciones sin repetición vimos el triángulo de Pascal y los coeficientes binomiales. Por ejemplo, para desarrollar (x+y)3 usamos los coeficientes binominales C(3, j) con el índice 0 ≤ j ≤ 3, que son también los que están en la fila 3 del triángulo de Pascal 1, 3, 3, 1, como se observa en la Figura.
El desarrollo sería el siguiente:
Si los coeficientes binomiales anteriores desarrollan el Binomio de Newton para dos variables { x, y }, los coeficientes multinomiales generalizan a cualquier número de variables { x, y, z, ... }. Por ejemplo, para desarrollar (x+y+z)4 partimos de tres variables { x, y, z }, tomando ese conjunto de partida con 3 letras distintas permutándolas con repetición en grupos de n=4 letras, veremos que se generan los coeficientes multinomiales { 1, 4, 6, 12 }:
En el primer paso ponemos todas las posibilidades de escribir con las letras { x, y, z } en 4 posiciones, repitiendo letras siempre, pues hay más posiciones que letras. Así tenemos {xxxx, yyyy, zzzz, xxxy, xxxz, xyyy, ...} como vemos en lo anterior, donde separamos las letras con un espacio para indicar que implica un operador producto. A cada caso le aplicamos la fórmula de las permutaciones con repetición, recordando como era en [1] o, expresado de otra forma, en [3] que volvemos a repetir a continuación, donde ∑i=1..m ri = n, con 0 ≤ ri ≤ n:
| PR(r1, r2, ..., rm) = | n! |
| ∏j=1..m rj! |
Para (x+y+z)4 tenemos que m=3 y n=4, donde r1+r2+r3 = 4
| PR(r1, r2, r3) = | 4! |
| ∏j=1..3 rj! |
Con la permutación "xxxx" tenemos PR(4, 0, 0) = PR(4) = 1, pues hay 4 "x", 0 "y", 0 "z". Solo hay una forma de permutar con repetición cuatro letras repetidas. Para el último caso "xyzz" tenemos:
| PR(1, 1, 2) = | 4! | = 12 |
| 1! 1! 2! |
Resolviendo todos los valores como PR(1, 1, 2), para lo cual puede usar la calculadora con esa misma expresión, y también expresando las multiplicaciones de variables con exponentes nos queda:
Expresión que finalmente podemos poner de forma compacta así, separando en cada línea por coeficiente del conjunto que ya habíamos comentado { 1, 4, 6, 12 }:
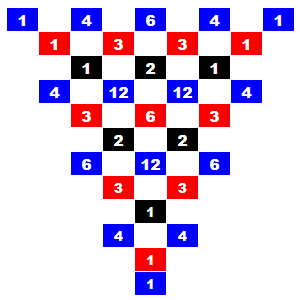
Para ver como se generan los coeficientes multinomiales, puede consultar en Wikipedia el tema Pascal's pyramid. En lugar de un triángulo de Pascal para desarrollar dos variables { x, y } ahora hablamos de una pirámide de Pascal para desarrollar tres variables { x, y, z }.
En la Figura puede ver una representación de la pirámide de Pascal con presentación de las capas 2 a 4. Al ser la pirámide un objeto de 3 dimensiones no es fácil representarlo en 2 dimensiones. Lo que se representa son capas o rodajas horizontales de la pirámide como si la viésemos desde arriba. Una capa de una pirámide es, por supuesto, un triángulo. Y suele ponerse invertido para no confundirlo con el triángulo de Pascal.
En la imagen vemos desde la parte de arriba de la pirámide tres capas: la negra es la capa 2 que estaría más arriba, la roja es la capa 3 intermedia y al fondo la azul es la capa 4. Es esta la que contiene los coeficientes del desarrollo (x+y+z)4 que vimos antes. Cada capa es, individualmente, como sigue:
Capa 0: 1
Capa 1: 1 1
1
Capa 2: 1 2 1
2 2
1
Capa 3: 1 3 3 1
3 6 3
3 3
1
Capa 4: 1 4 6 4 1
4 12 12 4
6 12 6
4 4
1La primera línea en cada capa conforma el triángulo de Pascal:
Capa 0: 1 Capa 1: 1 1 Capa 2: 1 2 1 Capa 3: 1 3 3 1 Capa 4: 1 4 6 4 1
La pirámide de Pascal representa los coeficientes para desarrollar 3 variables { x, y, z }. De igual forma podríamos hablar de desarrollar más variables, pero no es fácil representar gráficamente más dimensiones. Puede ver más en el tema de Wikipedia Pascal's simplex. En cualquier caso el proceso para desarrollarlo sería como hicimos antes. Por ejemplo, para el sencillo caso con 4 variables (v+x+y+z)2 tendríamos los coeficientes { 1, 2 }: