Funciones generadoras en una variable
Funciones generadoras para resolver recurrencias
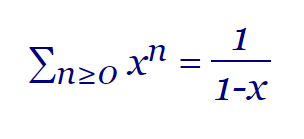
Para analizar el coste de un recursivo de una variable vimos varias posibilidades, como desarrollar la recurrencia hasta el caso trivial o equipararla a una ecuación característica. Son técnicas básicas para recurrencias simples como T(n). Pero si la recurrencia es más compleja o incluye dos variables T(n, k), entonces hemos de aplicar la técnica de la función generadora que veremos en estos temas.
En el tema siguiente veremos recurrencias de dos variables como T(n, k) que resolveremos con la función generadora. Previamente para practicar esta técnica resolveré algunos ejemplos simples con una variable, tomando los mismos problemas expuestos en los temas de recursivos que señalamos antes.
Dado que no resulta fácil escribir fórmulas matemáticas directamente en HTML, en lo que sigue abreviaremos expresiones como las series, expresando el rango n ∈ [a, b] como n=a..b
Por otro lado el rango [0, ∞] se puede abreviar en las series con n≥0
Y también con dos variables:
Con estas simplificaciones mantenemos un HTML no demasiado extenso y lo más legible posible.
Como vemos en Wikipedia, la función generadora o generatriz es una serie formal de potencias cuyos coeficientes codifican información sobre una sucesión an cuyo índice corre sobre los enteros no negativos
. Una definición que podemos entender mejor con la función generadora que vemos en la Figura:
| ∑n≥0 xn = | 1 |
| 1-x |
Esta es una serie geométrica sobre la que entraremos con más detalle en un apartado más abajo. Por ahora observe que
donde tenemos la sucesión de coeficientes an = 1, 1, 1, ... que se pueden generar con la serie ∑n≥0 1 xn, serie que se obtiene a partir del desarrollo de la función generadora. Este desarrollo puede hacerse usando la fórmula Taylor:
| f(x) = | 1 | = ∑n≥0 | f n(0) | xn |
| 1-x | n! |
donde las derivadas f n(x) son las siguientes:
| f 0(x) = | 1 |
| 1-x |
| f 1(x) = | 1 |
| (1-x)2 |
| f 2(x) = | 2 |
| (1-x)3 |
| f 3(x) = | 6 |
| (1-x)4 |
| f 4(x) = | 24 |
| (1-x)5 |
Con sólo estos términos podemos ver que particularizando para x=0 solo nos queda la secuencia de numeradores 1, 1, 2, 6, 24, ... = 0!, 1!, 2!, 3!, 4!, ... = n!, así que para todo n tenemos
| f n(0) | = 1 |
| n! |
de tal forma que
| 1 | = ∑n≥0 1 xn |
| 1-x |
Si tuviéramos una recurrencia como la siguiente
La función generadora y su serie serían precisamente esas. Y el término general an = 1 en la serie es la solución a la recurrencia, es decir, T(n) = 1 es la solución, lo que puede parecer obvio, pero es lo que se deduce de esta técnica. En los problemas siguientes veremos soluciones no tan obvias.
Pasos para aplicar la función generadora a una recurrencia
Resumimos los pasos para aplicar la función generadora para resolver una recurrencia. Pondremos como ejemplo los obtenidos en el problema del factorial que veremos en el apartado siguiente:
- Plantear la recurrencia: T(n) = T(n-1) + 1, definiendo las condiciones iniciales T(0)= 1.
- Ajustar la recurrencia para evitar índices negativos: T(n+1) = T(n) + 1, T(0) = 1.
- Definir la función generadora: Gn(x) = ∑n≥0 T(n) xn.
- Determinar las condiciones iniciales de la función generadora: G0(x) = 1.
- Multiplicar por xn y sumar todos los términos de la recurrencia:∑n≥0 T(n+1) xn = ∑n≥0 T(n) xn + ∑n≥0 xn
- Identificar Gn(x) así como también expresando T(n+1) en función de T(n) y a su vez en función de Gn(x).
- Identificar series directamente como la geométrica que vimos en el primer apartado:
∑n≥0 xn = 1 1-x - Finalmente llegaremos a una expresión que nos permitirá despejar Gn(x):
1 (Gn(x) - 1) = Gn(x) + 1 x 1-x - Despejaremos Gn(x) para obtener siempre un cociente de polinomios:
Gn(x) = 1 (1-x)2 - Expresar Gn(x) = ∑n≥0 f(n) xn como una serie. Cuando lo tengamos podemos deducir que el término general f(n) de este serie es igual que el que estamos buscando T(n). Para determinar esa serie es recomendable simplificar Gn(x) en fracciones simples y buscar una serie para cada término más fácilmente. Una forma de determinar una serie es usando el desarrollo de Taylor que ya vimos en el apartado anterior:
f(x) = ∑n≥0 f n(0) xn n! - Finalmente tendremos la solución:Gn(x) = ∑n≥0 (n+1) xn ⇒ T(n) = n+1
El factorial: resolver con función generadora
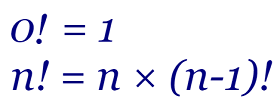
En la serie de temas sobre los recursivos vimos cómo calcular el coste de la función recursiva factorial. Este recursivo es muy simple, pues n! = n × (n-1)! con la condición inicial 0! = 1. Su simplicidad nos pemitirá exponer la técnica de la función generadora para calcular el coste.
Empecemos por recordar el algoritmo y la recurrencia:
function factorial(n){
if (n===0){
return 1;
} else {
return n*factorial(n-1);
}
}| T(n) = { | 1 | si n=0 |
| T(n-1) + 1 | si n>0 |
O puesta de manera compacta podemos expresarla así:
No debe confundirse esta recurrencia del algoritmo recursivo que implementa el cálculo del factorial con el del propio factorial que obedece a la recurrencia que vemos en la Figura y que podemos expresar como P(0)=1, P(n) = n × P(n-1).
Todas las recurrencias que vemos en este tema son recurrencias lineales con coeficientes constantes, pues con el término recursivo (1) × T(n-1) se acompaña una constante, un 1 en este caso. Mientras que la del cálculo del factorial n × P(n-1) tenemos la variable n. Estas recurrencias las veremos en el tema posterior recurrencias con coeficientes variables. Volveremos a ella también en el tema caso base genérico.
Esta recurrencia también podemos expresarla así para evitar el índice n-1 (más abajo explicaremos el motivo):
Definimos una función generadora
Para ser coherentes deberíamos denominar Gn(x) a la función generadora. También lo he visto escrito como G(an; x). Pero para simplificar omitimos la n. A veces necesitaremos expresarlo así, como con las condiciones iniciales:
Multiplicamos la recurrencia T(n+1) = T(n) + 1 en ambos lados por xn:
Y sumamos ambos lados
Antes de seguir, vea que si no hubiésemos evitado el índice n-1 podríamos tener un problema al aplicar la función generadora, pues tendríamos un término T(-1) que no está definido en la recurrencia ni, por tanto, en el algoritmo:
En la parte derecha de [1] tenemos ∑n≥0 T(n) xn = G(x). Y el otro sumando es una serie geométrica que converge para |x|<1:
| ∑n≥0 xn = | 1 |
| (1-x) |
Veamos el lado izquierdo
Multiplicando por x/x
| ∑n≥0 T(n+1) xn = | x | ( T(1) + T(2) x + T(3) x2 + ... ) = |
| x |
| = | 1 | ( T(1) x + T(2) x2 + T(3) x3 + ... ) |
| x |
Sumamos y restamos T(0)
| ∑n≥0 T(n+1) xn = | 1 | ( T(0) + T(1) x + T(2) x2 + T(3) x3 + ... - T(0) ) |
| x |
Lo resaltado es G(x) y como T(0) = 1 queda finalmente
| ∑n≥0 T(n+1) xn = | 1 | (G(x) - 1) |
| x |
Con esto la expresión final [1] queda como sigue:
| 1 | (G(x) - 1) = G(x) + | 1 | ⇒ |
| x | 1-x |
| G(x) = | x | + | 1 |
| (1-x)2 | 1-x |
Para encontrar el término general para T(n) hemos de expandir G(x) usando series. Podemos descomponer en fracciones simples el primer término de la expresión de la derecha:
| x | = - | 1 | + | 1 |
| (1-x)2 | 1-x | (1-x)2 |
Con lo que finalmente nos queda:
| G(x) = - | 1 | + | 1 | + | 1 | = | 1 |
| 1-x | (1-x)2 | 1-x | (1-x)2 |
Una vez que tengamos la función generadora tenemos que expresarla como una serie
| G(x) = | 1 |
| (1-x)2 |
A partir de aquí tenemos varias posibilidades. Una de ellas es usando el desarrollo de Taylor que ya vimos en el primer apartado:
| G(x) = | 1 | = ∑n≥0 | G n(0) | xn |
| (1-x)2 | n! |
Calculamos las primeras derivadas:
| G 0(x) = | 1 |
| (1-x)2 |
| G 1(x) = | 2 |
| (1-x)3 |
| G 2(x) = | 6 |
| (1-x)4 |
| G 3(x) = | 24 |
| (1-x)5 |
| G 4(x) = | 120 |
| (1-x)6 |
Con sólo estos términos podemos ver que particularizando para x=0 solo nos queda la secuencia de numeradores 1, 2, 6, 24, 120, ... = 1!, 2!, 3!, 4!, 5!, ... = (n+1)!, así que para todo n≥0 tenemos
| G n(0) | = | (n+1)! | = | (n+1) n! | = n+1 |
| n! | n! | n! |
Esta hipótesis habría que demostrarla usando alguna técnica, como la demostración por inducción. Puede ver un ejemplo en el siguiente apartado. Una vez demostrado podemos asegurar que la serie que le corresponde a G(x) es:
| G(x) = | 1 | = ∑n≥0 (n+1) xn |
| (1-x)2 |
Alternativamente podemos usar otras técnicas como la siguiente. Ya vimos que la suma geométrica era
| 1 | = ∑n≥0 xn = 1 + x + x2 + x3 + ... |
| 1-x |
Si derivamos las expresiones tenemos:
| d | ( | 1 | ) = | 1 | = |
| dx | 1-x | (1-x)2 |
| = | d | (1 + x + x2 + x3 + ...) = 0 + 1 + 2x + 3x2 + ... = ∑n≥0 (n+1) xn |
| dx |
Por lo tanto
| ∑n≥0 (n+1) xn | = | 1 | = G(x) |
| (1-x)2 |
Sea de una forma u otra, finalmente hemos obtenido la solución de la recurrencia:
Como partimos definiendo G(x) = ∑n≥0 T(n) xn resulta que el término general de la recurrencia que buscamos es:
Y este es el mismo resultado que encontramos usando la ecuación característica.
Las torres de Hanoi: resolver con función generadora
Veamos ahora la recurrencia de las torres de Hanoi, otro problema que ya resolvimos usando la técnica de la ecuación característica.
El problema se basa en que tenemos 3 postes y un número n de discos de diferentes radios en uno de los postes, de tal forma que están ordenados de mayor a menor. Tenemos que pasar esos discos a otro poste pero con la restricción de que en cada movimiento sólo podemos pasar un disco. Y que en ningún caso podrá haber un disco de mayor radio sobre otro menor, es decir, siempre tendrán que estar ordenados de forma decreciente.
Este era el algoritmo que utilizábamos:
function hanoi(postes, i=0, j=1, n=postes[i].length){
if (n===0) {
//caso trivial
} else {
let p = n-1;
let k = 3-i-j;
hanoi(postes, i, k, p);
postes[j].push(postes[i].pop());
hanoi(postes, k, j, p);
}
}Y así definíamos la recurrencia:
| T(n) = | { | 1 | si n=0 |
| 2 T(n-1) + 1 | si n>0 |
Esta recurrencia también podemos expresarla así para evitar el índice n-1, cuya necesidad ya explicamos en el apartado anterior:
Definimos una función generadora:
Determinamos las condiciones iniciales:
Multiplicamos la recurrencia por xn y sumamos
| = 2 ∑n≥0 T(n) xn + ∑n≥0 xn = 2 G(x) + | 1 |
| 1-x |
Veamos la parte izquierda ∑n≥0 T(n+1) xn como hicimos en el desplegable del primer apartado
De donde
| ∑n≥0 T(n+1) xn = | 1 | ( G(x) - 1 ) |
| x |
| 1 | ( G(x) - 1 ) | = 2 G(x) + | 1 |
| x | 1-x |
Despejando obtenemos:
| G(x) = | 1 |
| (1-x)(1-2x) |
Descomponemos el cociente de polinomios
| 1 | = | 2 | - | 1 |
| (1-x)(1-2x) | 1-2x | 1-x |
Por lo que
| G(x) = | 2 | - | 1 |
| 1-2x | 1-x |
Una vez obtenida la función generadora, hemos de equipararla a una serie para localizar el término general. En la parte derecha tenemos la función generadora de la suma geométrica, cuya serie conocemos:
| 1 | = ∑n≥0 xn |
| 1-x |
Desarrollemos con Taylor el otro componente que denominaremos f(x):
| f(x) = | 2 | = ∑n≥0 | f n(0) | xn |
| 1-2x | n! |
Calculamos las primeras derivadas:
| f 0(x) = | 2 |
| 1-2x |
| f 1(x) = | 4 |
| (1-2x)2 |
| f 2(x) = | 16 |
| (1-2x)3 |
| f 3(x) = | 96 |
| (1-2x)4 |
Particularizadas para x=0 tenemos
En la sucesión anterior 2, 4, 16, 96,... hemos hecho una suposición para el término general 2n+1 n!, pudiendo demostrarse por inducción matemática el término general de la derivada n-ésima:
| f n(x) = | 2n+1 n! |
| (1-2x)n+1 |
Y este término particularizado para n=0 es:
Entonces el desarrollo de Taylor queda:
| f(x) = | 2 | = ∑n≥0 | f n(0) | xn | = ∑n≥0 | 2n+1n! | xn = ∑n≥0 2n+1 xn |
| 1-2x | n! | n! |
Tomando [5] y [6] y sustituyendo en [4] y operando la suma de series:
| G(x) = | 2 | - | 1 | = ∑n≥0 2n+1 xn - ∑n≥0 xn = |
| 1-2x | 1-x |
Como partimos definiendo G(x) = ∑n≥0 T(n) xn resulta que el término general de la recurrencia que buscamos es:
Y este es el mismo resultado que encontramos usando la ecuación característica.
Fibonacci: resolver con función generadora
En el tema de Fibonacci vimos esta función recursiva que se define como f(0)=0, f(1)=1 y f(n) = f(n-1) + f(n-2) para n≥2. Los primeros téminos de la sucesión son 0, 1, 1, 2, 3, 5, 8, 13, 21,... La espiral de Fibonacci de la Figura representa esta sucesión como arcos de cuadrante inscritos en rectángulos cuyos lados siguen esta sucesión.
En ese tema usamos la técnica de la ecuación característica para obtener la solución. Repetimos este problema usando la técnica de la función generadora. El algoritmo usado era el siguiente:
function fibonacci(n){
if (n<2){
return n;
} else {
return fibonacci(n-1) + fibonacci(n-2);
}
}Definíamos la recurrencia así:
| T(n) = | { | 1 | si n<2 |
| T(n-1) + T(n-2) + 1 | si n≥2 |
Evitamos los índices negativos, pudiendo entonces expresar la recurrencia así:
Usamos la misma función generadora que en los ejemplos anteriores:
Las condiciones iniciales son:
Aplicamos xn a la recurrencia y sumamos:
Como en casos anteriores, en la derecha tenemos la suma geométrica:
| ∑n≥0 xn = | 1 |
| 1-x |
Expresemos el término T(n+2) en función de T(n):
Obteniendo el término T(n+2)
| ∑n≥0 T(n+2) xn = | 1 | (G(x) - x - 1) |
| x2 |
Y ahora el término T(n+1)
Por lo tanto
| ∑n≥0 T(n+1) xn = | 1 | (G(x) - 1) |
| x |
Sustituyendo [7], [9], [10] y [11] en [8]
| 1 | (G(x) - x - 1) = | 1 | (G(x) - 1) + | G(x) + | 1 |
| x2 | x | 1-x |
Obteniendo la función generadora siguiente:
| G(x) = | x2-x+1 | = | x2-x+1 |
| (x-1)(x2+x-1) | (1-x)(1-x-x2) |
No parece fácil aplicar el desarrollo de Taylor a esta expresión para deducir su serie. Intentemos simplificar:
| x2-x+1 | = | A | + | B | = |
| (1-x)(1-x-x2) | 1-x | 1-x-x2 |
| = | A-Ax-Ax2+B-Bx | = | -Ax2-(A+B)x+(A+B) |
| (1-x)(1-x-x2) | (1-x)(1-x-x2) |
Entonces
Por lo tanto de la primera ecuación A = -1 y de la segunda B = 1-A = 2, valores que cumplen la tercera ecuación A+B = 2-1 = 1. Entonces la función generadora [12] nos queda así:
| G(x) = - | 1 | + | 2 |
| 1-x | 1-x-x2 |
El primer término ya sabemos que es la serie geométrica ∑n≥0 xn. Hemos de obtener una serie para el segundo término. Como 1-x-x2 = -(x2+x-1) buscaremos las raíces de la ecuación de segundo grado x2+x-1:
| r1 = - | 1 + √5 | , |
| 2 |
| r2 = - | 1 - √5 |
| 2 |
Sea
| Φ = -r1 = | 1 + √5 | , |
| 2 |
| δ = -r2 = | 1 - √5 |
| 2 |
Observe estas propiedades de Φ y δ, pues algunas de ellas nos servirán posteriormente:
- Φ+δ = 1
- Φ-δ = √5
- Φδ = -1 ⇒ Φ = - ⅟δ ∧ δ = - ⅟Φ
Entonces
| = -(x+Φ)(x+δ) | δΦ | = - | δ(x+Φ) Φ(x+δ) | = |
| Φδ | Φδ |
| = - | (δx+δΦ) (Φx+Φδ) | = (δx-1) (Φx-1) | = |
| Φδ |
Con esto el segundo término de la función generadora [13] nos queda así, donde nuevamente desarrollamos en fracciones:
| 2 | = | 2 | = | 2 | ( | Φ | - | δ | ) |
| 1-x-x2 | (1-Φx)(1-δx) | Φ-δ | 1-Φx | 1-δx |
Ahora estamos en condiciones de encontrar una serie para cada uno de los términos entre paréntesis. Vease que una serie geométrica de razón ax es:
| 1 | = ∑n≥0 (ax)n |
| 1-ax |
Viendo que Φ-δ = √5 nos queda
| 2 | = | 2 | ( | Φ | - | δ | ) = |
| 1-x-x2 | Φ-δ | 1-Φx | 1-δx |
| = | 2 | ( ∑n≥0 Φn+1 xn - ∑n≥0 δn+1 xn ) = |
| √5 |
| = ∑n≥0 | 2 | ( Φn+1 - δn+1 ) xn |
| √5 |
Sin usar el "truco" que nos permitió obtener 1-Φx y 1-δx que nos facilitó el uso de series geométricas, podemos aplicar cálculos usando Taylor y desarrollando hasta alcanzar el mismo resultado, aunque con más esfuerzo, como se muestra en el siguiente desplegable.
Finalmente, volviendo a la función generadora [13]:
| G(x) = - | 1 | + | 2 | = |
| 1-x | 1-x-x2 |
| = - ∑n≥0 xn + ∑n≥0 | 2 | ( Φn+1 - δn+1 ) xn = |
| √5 |
| = ∑n≥0 ( | 2 | ( Φn+1 - δn+1 ) - 1) xn |
| √5 |
Por lo tanto el término general es
| T(n) = | 2 | ( Φn+1 - δn+1 ) - 1 |
| √5 |
Y este el mismo resultado que obtuvimos con la ecuación característica, aunque con mucho más trabajo.
Recurrencia de la función Fibonacci
No debe confundirse nuestra recurrencia que se define a partir del algoritmo como:
| T(n) = | { | 1 | si n<2 |
| T(n-1) + T(n-2) + 1 | si n≥2 |
con la recurrencia para resolver la función de Fibonacci:
| F(n) = | { | 0 | si n=0 |
| 1 | si n=1 | ||
| F(n-1) + F(n-2) | si n≥2 |
Ajustamos esta función para evitar índices negativos:
Con esta función las condiciones iniciales son diferentes:
Vea que G0 es cero cuando en nuestro problema era uno. Además esta recurrencia no tiene el término 1 señalado más arriba, con lo que la expresión [8] que vimos en nuestro problema quedaría así:
Haciendo el mismo proceso para obtener F(n+2) y F(n+1) como hicimos en nuestro problema, pero ahora teniendo en cuenta que la condición inicial G0(x) = 0 es distinta, llegaríamos a la expresión siguiente, ligeramente diferente a la que obtuvimos:
| 1 | (G(x) - x) = | 1 | G(x) + G(x) |
| x2 | x |
Al resolverla obtenemos esto, también algo diferente, aunque con el mismo polinomio en el denominador 1-x-x2:
| G(x) = | x | = |
| 1-x-x2 |
| = | x | = |
| -(x+Φ)(x+δ) |
| = | 1 | ( | 1 | - | 1 | ) |
| Φ - δ | 1-Φx | 1-δx |
Con esa expresión aplicando las mismas raíces Φ, δ como hicimos en el apartado anterior llegaríamos a obtener esta solución, también diferente en algunas cosas con la nuestra:
| F(n) = | 1 | ( Φn - δn ) |
| √5 |
Relación entre la función generadora y la ecuación característica
En este apartado vamos a analizar para los tres ejemplos lo que resolvimos con la ecuación característica y como lo resolvimos en este tema con la función generadora. Intentaré saber cuál es el motivo de que no siempre aparezca exactamente la misma ecuación característica en el denominador de la función generadora. Si es que hay alguna relación entre ambas cosas.
El factorial
Empecemos por el tema del factorial, donde obtuvimos la ecuación característica siguiente:
cuyas raices r = 1 de multiplicidad 2 nos permitían obtener la solución general
Obteníamos las constantes a partir de las condiciones iniciales, obteniendo finalmente la solución exacta siguiente
Esa solución es la misma que la obtenida con la técnica de la función generadora
| G(x) = | x | + | 1 | = | 1 |
| (1-x)2 | 1-x | (1-x)2 |
Observe que la ecuación característica es "casi" la misma que el polinomio del denominador. Es la misma pues (x-1)2 = (1-x)2 es una potencia par, donde se iguala el posible signo negativo interior. Pero esa "leve" diferencia entre x-1 y 1-x tiene una razón de ser que explicaremos mejor con el siguiente ejemplo.
Torres de Hanoi
En el ejemplo torres de Hanoi obteníamos esta ecuación característica que vamos a denominar R(x):
Las raíces r = 1, r = 2, ambas de multiplicidad uno, nos daban la solución general y la solución exacta al aplicar las condiciones iniciales:
Esa solución exacta es la misma que la que obtuvimos con la función generadora:
| G(x) = | 2 | - | 1 | = | 1 | = | P(x) |
| 1-2x | 1-x | (1-x)(1-2x) | Q(x) |
Al estar esta fracción de polinomios ya en un estado de irreducible, P(x) es necesariamente de un grado inferior a Q(x). Entonces ¿qué relación hay entre R(x) y Q(x)? Las raíces de Q(x) son q = 1, q = ½ ambas de multiplicidad uno, pero diferente una de ellas de las de R(x). Para resolverlo necesitamos la siguiente definición.
Dos polinomios Q(x) y R(x) son polinomios recíprocos o reflejados si para cada término se cumple que ai xi = an-i xi lo que supone invertir los coeficientes:
Dos polinomios Q(x) y R(x) recíprocos cumplen estas propiedades:
- d = deg R = deg Q (El operador deg es el grado del polinomio)
- R(x) = xd Q(⅟x)
- r es raíz de R ⇔ ⅟r es raíz de Q
- Si R(x)≠x ⇒ R es irreducible ⇔ Q es irreducible
- R es primitivo ⇔ Q es primitivo
Nuestros dos polinomios son recíprocos, pues tienen los coeficientes invertidos:
Se cumple que ambos tienen el mismo grado:
Se cumple que las raíces de uno son las recíprocas del otro:
También se cumple R(x) = xd Q(⅟x), pues aplicándolo a Q(x) = 1-3x+2x2
| x2 Q(⅟x) = x2 (1- | 3 | + | 2 | ) = x2-3x+2 = R(x) |
| x | x2 |
También podemos aplicarlo a cada término de Q(x) = (1-x)(1-2x) así:
| x2 Q(⅟x) = x (1- | 1 | ) x (1- | 2 | ) = (x-1)(x-2) = x2-3x+2 = R(x) |
| x | x |
En estas condiciones podemos decir que R(x) = (x-2)(x-1) = x2-3x+2 es la única ecuación característica de la recurrencia de las Torres de Hanoi que habíamos planteado. Cada recurrencia tiene una única ecuación característica y, al revés, a cada ecuación característica le corresponde una única recurrencia. En el polinomio del denominador de la función generadora tenemos el recíproco de la ecuación característica.
Fibonacci
Lo mismo sucede con el problema de Fibonacci, donde teníamos la siguiente ecuación característica:
Con tres raíces de multiplicidad uno:
Siendo
| Φ = | 1 + √5 | , |
| 2 |
| δ = | 1 - √5 |
| 2 |
En este tema hemos obtenido la siguiente función generadora:
| G(x) = - | 1 | + | 2 | = | x2-x+1 | = | x2-x+1 | = | P(x) |
| 1-x | 1-x-x2 | (1-x)(1-x-x2) | x3-2x+1 | Q(x) |
Obteníamos la misma solución con ambas técnicas:
| T(n) = | 2 | ( Φn+1 - δn+1 ) - 1 |
| √5 |
El cociente de polinomios P(x) / Q(x) está ya expresado de una forma irreducible, con el grado del numerador deg P(x) = 2 menor que el del denominador deg Q(x) = 3:
Vemos que Q(x) y R(x) son recíprocos pues tienen los coeficientes invertidos. Se observa mejor si los ponemos así:
Las raíces de Q(x) son q1 = 1, q2 = -Φ = ⅟δ , q3 = -δ = ⅟Φ que son las recíprocas de las de R(x). Recuerde que vimos en el apartado de la función generadora de Fibonacci las propiedades de Φ y δ.
Ademas se cumple R(x) = xd Q(⅟x):
| x3 Q(⅟x) = x3 ( | 1 | - | 2 | +1 ) = 1-2x2+x3 = R(x) |
| x3 | x |
Al ser R(x) y Q(x) recíprocos entonces R(x) es la única ecuación característica que le corresponde a la recurrencia dada en nuestro problema.