Desarreglos parciales
Calcular el valor numérico de los desarreglos parciales
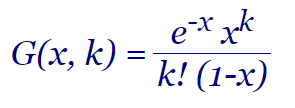
Los desarreglos parciales (partial derangements) de una lista con n elementos distintos son todas las sublistas ordenadas con n elementos distintos que se pueden generar de tal forma que solo k elementos aparecen en su posición original. También se pueden definir como las permutaciones de n elementos con k puntos fijos. Las denotamos como D(n, k), correspondiendo con k=0 a los desarreglos sin puntos fijos que vimos en un tema anterior.
También se les denomina Rencontres numbers traducido como Problema de encuentros (o reencuentros). La función generadora de esta familia de funciones combinatorias es como sigue:
| G(x, k) = | e-x xk |
| k! (1-x) |
Como hemos dicho, el caso k=0 ya lo vimos en los temas desarreglos y desarreglos recursivo, con lo que D(n, 0) = D(n), donde implementamos sendos algoritmos para su generación. Los primeros ejemplos hasta n=4 de desarreglos D(n, 0), que ya expusimos en el primer tema señalado, son:
| List | n | Result | D(n, 0) |
|---|---|---|---|
| [] | 0 | {[]} | 1 |
| [a] | 1 | {} | 0 |
| [a, b] | 2 | {[b, a]} | 1 |
| [a, b, c] | 3 | {[c, a, b], [b, c, a]} | 2 |
| [a, b, c, d] | 4 | {[b,a,d,c],[d,a,b,c],[b,d,a,c],[c,a,d,b],[c,d,a,b],[d,c,a,b],[d,c,b,a],[c,d,b,a],[b,c,d,a]} | 9 |
Observamos que en cada desarreglo o permutación ningún elemento aparece en su posición original.
Veamos el caso k=1 donde habrá un único elemento en su posición original que hemos resaltado en color azul:
| List | n | Result | D(n, 1) |
|---|---|---|---|
| [] | 0 | {} | 0 |
| [a] | 1 | {[a]} | 1 |
| [a, b] | 2 | {} | 0 |
| [a, b, c] | 3 | {[a,c,b], [c,b,a], [b,a,c]} | 3 |
| [a, b, c, d] | 4 | {[a,c,d,b], [a,d,b,c], [c,b,d,a], [d,b,a,c], [b,d,c,a],[d,a,c,b], [b,c,a,d], [c,a,b,d]} | 8 |
En el siguiente apartado veremos que el número de desarreglos con k puntos fijos de una lista con n elementos se calcula con la siguiente fórmula:
Recurrencia que calcula el número de desarreglos parciales
Partiendo de la recurrencia de los desarreglos sin puntos fijos que vimos en un tema anterior D(n) = (n-1) D(n-1) + (n-1) D(n-2) planteamos que la recurrencia para calcular el número de desarreglos parciales de n elementos con k puntos fijos es la siguiente, lo que demostraremos como cierto si a partir de ella se consigue obtener el término general D(n, k) = C(n, k) × D(n-k, 0)
| D(n, k) = | n(n-k-1) | D(n-1, k) + | n(n-1) | D(n-2, k) |
| n-k | n-k |
Cuando k=0 estamos en el caso de desarreglos sin puntos fijos, cuya recurrencia vimos en ese tema de los desarreglos, cuya solución es el subfactorial D(n) = !n
D(n) = (n-1) D(n-1) + (n-1) D(n-2)
Veamos si podemos resolver la recurrencia [2], donde k no es una variable de la recurrencia, sino un parámetro, pues mantiene su valor en las sucesivas llamadas. Por lo tanto a efectos de realizar desarrollos matemáticos la expresamos así, como una recurrencia de una única variable n:
| D(n) = | n(n-k-1) | D(n-1) + | n(n-1) | D(n-2) |
| n-k | n-k |
Podríamos fiarnos de WolframAlpha para llegar a obtener el resultado esperado (cambiando D(n, k) por a(n, k) para que no lo confunda con derivadas), obteniéndose en Wolfram Alpha lo siguiente sabiendo que Γ(n+1) = n! es la funcion Gamma:
| D(n, k) = !(n-k) | Γ(n+1) | = !(n-k) | n! | = !(n-k) C(n, k) |
| Γ(k+1) Γ(n-k+1) | k! (n-k)! |
Nos tranquiliza pensar que la recurrencia planteada es correcta, pues Wolfram Alpha obtiene lo esperado. Pero aún así vamos a aplicar la técnica de la función generadora para demostrarlo.
| G(x) = ∑n≥k D(n) | xn |
| n! |
Estas son las condiciones iniciales:
| Gk(x) = ∑n=k..k D(n) | xn | = D(k) | xk | = | xk |
| n! | k! | k! |
| Gk+1(x) = ∑n=k+1..k+1 D(n) | xn | = D(k+1) | xk+1 | = 0 |
| n! | (k+1)! |
Incrementando índices la recurrencia [4]
| D(n+2) = | (n+2)(n-k+1) | D(n+1) + | (n+2)(n+1) | D(n) |
| n-k+2 | n-k+2 |
Operando para dejar libre D(n)
| n-k+2 | D(n+2) = | n-k+1 | D(n+1) + D(n) |
| (n+2)(n+1) | n+1 |
Aplicando la función generadora a esta recurrencia
| ∑n≥k | n-k+2 | D(n+2) | xn | = ∑n≥k | n-k+1 | D(n+1) | xn | + ∑n≥k D(n) | xn |
| (n+2)(n+1) | n! | n+1 | n! | n! |
Resolviendo el término de la izquierda
| ∑n≥k | n-k+2 | D(n+2) | xn | = |
| (n+2)(n+1) | n! |
| = ∑n≥k (n-k+2) D(n+2) | xn | = |
| (n+2)! |
| = ∑n≥k (n-k+2) D(n+2) | xn+2 x-2 | = |
| (n+2)! |
| = | 1 | ∑n≥k (n-k+2) D(n+2) | xn+2 | = |
| x2 | (n+2)! |
| = | 1 | ( ∑n≥k (n+2) D(n+2) | xn+2 | - k ∑n≥k D(n+2) | xn+2 | ) = |
| x2 | (n+2)! | (n+2)! |
| = | 1 | ( ∑n≥k+2 n D(n) | xn | - k ∑n≥k+2 D(n) | xn | ) = |
| x2 | n! | n! |
| = | 1 | ( (- 0 + ∑n≥k+1 n D(n) | xn | ) - (- 0 + k ∑n≥k+1 D(n) | xn | ) ) = |
| x2 | n! | n! |
| = | 1 | ( ∑n≥k+1 n D(n) | xn | - k ∑n≥k+1 D(n) | xn | ) |
| x2 | n! | n! |
En el penúltimo paso hemos ajustado el índice de los sumatorios desde n≥k+2 a n≥k+1, con lo que restamos un término que contiene D(k+1) = 0 pues este es el segundo caso base, así que tenemos esos dos ceros resaltados.
Resolviendo el término de la derecha en [8]
| ∑n≥k | n-k+1 | D(n+1) | xn | = |
| n+1 | n! |
| = ∑n≥k (n-k+1) | D(n+1) | xn | = |
| (n+1)! |
| = ∑n≥k (n-k+1) | D(n+1) | xn+1 x-1 | = |
| (n+1)! |
| = | 1 | ( ∑n≥k (n-k+1) | D(n+1) | xn+1 | ) = |
| x | (n+1)! |
| = | 1 | ( ∑n≥k (n+1) | D(n+1) | xn+1 | - k ∑n≥k D(n+1) | xn+1 | ) = |
| x | (n+1)! | (n+1)! |
| = | 1 | ( ∑n≥k+1 n | D(n) | xn | - k ∑n≥k+1 D(n) | xn | ) |
| x | n! | n! |
| 1-x | ( ∑n≥k+1 n D(n) | xn | - k ∑n≥k+1 D(n) | xn | ) = ∑n≥k D(n) | xn |
| x2 | n! | n! | n! |
Vemos que la parte derecha es G(x) y ajustamos índices de los otros sumatorios:
| 1-x | ( - k D(k) | xk | + ∑n≥k n D(n) | xn | - k ( - D(k) | xk | + ∑n≥k D(n) | xn | ) ) = G(x) |
| x2 | k! | n! | k! | n! |
Como D(k)=1 del primer caso base y el segundo sumatorio también es G(x)
| 1-x | ( - | k xk | + ∑n≥k n D(n) | xn | + | k xk | - k G(x) ) = G(x) |
| x2 | k! | n! | k! |
entonces nos queda
| 1-x | ( x G'(x) - k G(x) ) = G(x) |
| x2 |
expresión que podemos poner así
| G'(x) | = | k | + | x |
| G(x) | x | 1-x |
Esto es una ecuación diferencial lineal ordinaria con coeficientes variables de primer orden, homogénea en este caso. Se resuelve integrando en ambos lados:
| ∫ | G'(x) | dx = ∫ | k | + | x | dx |
| G(x) | x | 1-x |
Pasando a la izquierda los logaritmos
Agrupando logaritmos
| log(G(x) | 1-x | ) = -x+c |
| xk |
Aplicando exponenciales
| G(x) | 1-x | = e-x ec |
| xk |
obteniendo finalmente la función generadora, tras generalizar la constante ec = c, constante que aún tenemos que determinar:
| G(x, k) = c | e-x xk |
| 1-x |
Para buscar el término general recordamos que es una recurrencia con caso base genérico, por lo que aplicaremos la técnica de actuar sobre el primer caso base [3], que ya hemos demostrado en el tema de desarreglos que su función generadora era:
| G(x, 0) = | e-x | = ∑n≥0 ( ∑j=0..n | (-1) j n! | ) | xn | = ∑n≥0 !n | xn |
| 1-x | j! | n! | n! |
Partiendo de eso
| e-x | = ∑n≥0 !n | xn | = | c xk | ∑n≥0 !n | xn | = | 1 | ∑n≥0 c !n | xn+k | = |
| 1-x | n! | c xk | n! | c xk | n! |
| = | 1 | ∑n≥k c !(n-k) | xn | = | 1 | ∑n≥k c !(n-k) | n! | xn | = |
| c xk | (n-k)! | c xk | n! | (n-k)! |
| = | 1 | ∑n≥k c !(n-k) | n! | xn |
| c xk | (n-k)! | n! |
Pasando c xk desde el denominador de la última expresión hasta el númerador de la primera obtenemos el término general para G(x, k):
| G(x, k) = c | e-x xk | = ∑n≥k c !(n-k) | n! | xn |
| 1-x | (n-k)! | n! |
Siendo el término general
| D(n, k) = c !(n-k) | n! |
| (n-k)! |
Para obtener la constante tenemos en cuenta las condiciones iniciales vistas en [6] y [7], teniendo en cuenta que !0 = 1:
| Gk(x, k) = | xk | = ∑n=k..k c !(n-k) | n! | xn | = c !(k-k) | k! | xk | = c xk |
| k! | (n-k)! | n! | (k-k)! | k! |
Entonces xk/k! = c xk ⇒ c = 1/k! obteniendo la constante con el primer caso base. Veamos que también cumple el segundo caso base teniendo en cuenta que !1 = 0:
| Gk+1(x, k) = 0 | = ∑n=k+1..k+1 c !(n-k) | n! | xn | = c !1 | (k+1)! | xk+1 | = c 0 = 0 |
| (n-k)! | n! | 1! | (k+1)! |
Se observa que se cumple que sea igual a cero pues !1 = 0, independientemente del valor de la constante. Entonces la función generadora es
| G(x, k) = | e-x xk | = ∑n≥k ( !(n-k) | n! | ) | xn |
| k! (1-x) | k! (n-k)! | n! |
Veáse que n!/(k! (n-k)!) = C(n, k) = V(n, k)/k! = nk/k! con lo que tenemos estas fórmulas equivalentes para el término general de los desarreglos parciales:
| D(n, k) = | V(n, k) | !(n-k) |
| k! |
| D(n, k) = | nk | !(n-k) |
| k! |
Como D(n, 0) = !n son los desarreglos sin puntos fijos entonces también podemos expresarlo así:
Se obtiene la siguiente tabla de primeros valores
| n | D(n, k) | ||||||
|---|---|---|---|---|---|---|---|
| k=0 | k=1 | k=2 | k=3 | k=4 | k=5 | k=6 | |
| 0 | 1 | ||||||
| 1 | 0 | 1 | |||||
| 2 | 1 | 0 | 1 | ||||
| 3 | 2 | 3 | 0 | 1 | |||
| 4 | 9 | 8 | 6 | 0 | 1 | ||
| 5 | 44 | 45 | 20 | 10 | 0 | 1 | |
| 6 | 265 | 264 | 135 | 40 | 15 | 0 | 1 |
Primer algoritmo para generar desarreglos parciales derangeP1(list, k)
Implementaremos el primer algoritmo para obtener los desarregos parciales basándonos en la última expresión del apartado anterior:
Veamos un ejemplo con la lista list = [a, b, c, d] que a veces escribiremos de forma compacta como list = abcd. Vamos a obtener los desarreglos parciales de esa lista que tiene una longitud n = 4 manteniendo dos puntos fijos k = 2. Vamos a obtener las desarreglos parciales o permutaciones con dos puntos fijos, cuyo número calculado es
En primer lugar vamos a transformar la lista list = abcd por otra listn = 0123. Dado que la lista inicial tiene un orden, lo que viene a ser un Array, vamos a gestionar sus posiciones más que sus valores. Así que las combinaciones de esta lista son:
Recuerde que esta forma compacta realmente quiere decir 01 ≡ [0, 1]. Siempre podremos recuperar los valores originales, pues por ejemplo
Por otro lado vamos a contemplar otra lista m = n-k = 4-2 = 2 elementos, creando la lista listm = 01. Los desarreglos o permutaciones sin puntos fijos de esta lista es de un único elemento D(2) = 1 con este único resultado
Vea que con la lista [0, 1] sólo hay una permutación sin puntos fijos que es [1, 0]. A continuación vamos a realizar el producto
derange(listm) × combine(listn, 2) = [ 10 ] × [ 01, 02, 03, 12, 13, 23 ]
Debemos obtener estos desarreglos parciales:
Observe que los que aparecen en negrita son los 2 puntos fijos o elementos que están en su posición original con respecto a la lista inicial abcd. El siguiente esquema genera el producto anterior:
list = [a, b, c, d] listn = [0, 1, 2, 3] listm = [0, 1] C = combine(listn, 2) D = derange(listm) Loop D = [[1, 0]] D[0] = [1, 0] Loop C = [[0,1], [0,2], [0,3], [1,2], [1,3], [2,3]] C[0] = [0, 1] subresult = [list[0], list[1], ?, ?] = [a, b, ?, ?] dnk = list - subresult = [c, d] subresult = [a, b, dnk[1], dnk[0]] = [a, b, d, c] C[1] = [0, 2] subresult = [list[0], ?, list[2], ?] = [a, ?, c, ?] dnk = list - subresult = [b, d] subresult = [a, dnk[1], c, dnk[0]] = [a, d, c, b] C[2] = [0, 3] subresult = [list[0], ?, ?, list[3]] = [a, ?, ?, d] dnk = list - subresult = [b, c] subresult = [a, dnk[1], dnk[0], d] = [a, c, b, d] C[3] = [1, 2] subresult = [?, list[1], list[2], ?] = [?, b, c, ?] dnk = list - subresult = [a, d] subresult = [dnk[1], b, c, dnk[0]] = [d, b, c, a] C[4] = [1, 3] subresult = [?, list[1], ?, list[3]] = [?, b, ?, d] dnk = list - subresult = [a, c] subresult = [dnk[1], b, dnk[0], d] = [c, b, a, d] C[5] = [2, 3] subresult = [?, ?, list[2], list[3]] = [?, ?, c, d] dnk = list - subresult = [a, b] subresult = [dnk[1], dnk[0], c, d] = [b, a, c, d] End Loop End Loop
Iteramos por las combinaciones construyendo cada desarreglo con la combinación que nos da la posición de los dos elementos fijos. Por ejemplo, en la primera iteración tenemos C[0] = [0, 1] con lo que el elemento "a" aparecerá en la posición cero y el "b" en la uno. Rellenamos el resto de posiciones "?" con el resto de elementos que son dnk = [c, d] en las posiciones que obtenemos del desarreglo D[0] = [1, 0], con lo que insertamos [d, c] en ese orden en cada "?", quedando finalmente [a, b, d, c], como el primer desarreglo parcial o permutación con los dos primeros puntos fijos.
Este algoritmo implementa lo anterior:
// D(n, k) = C(n, k) × D(n-k, 0)
function derangeP1(list=[], k=0){
iter +=1;
let result = [];
let n = list.length;
iter += n;
let listn = Array.from({length: n}, (v,i) => i);
let c = combine2(listn, k);
let m = Math.max(0, n-k);
iter += m;
let listm = Array.from({length: m}, (v,i) => i);
let d = derange1(listm);
for (let i=0; i<d.length; i++) {
iter += 1;
for (let p=0; p<c.length; p++){
iter += 1;
iter += n;
let dnkprev = [...list];
iter += n;
let subresult = Array.from({length: n}, () => "?");
for (let j=0; j<c[p].length; j++) {
iter += 1;
let pos = c[p][j];
subresult[pos] = list[pos];
dnkprev[pos] = "";
}
//let dnk = dnkprev.filter(v => v!=="");
//let dnk = list.filter(v => !subresult.includes(v));
let dnk = [];
for (let j=0; j<dnkprev.length; j++){
iter += 1;
if (dnkprev[j]!==""){
dnk.push(dnkprev[j]);
}
}
let q = -1;
for (let j=0; j<subresult.length; j++) {
iter += 1;
if (subresult[j]==="?") {
q++;
let pos = d[i][q];
subresult[j] = dnk[pos];
}
}
result.push(subresult);
}
}
return result;
}Vea que usamos los algoritmos vistos en temas anteriores combine2(list, k) para generar las combinaciones y derange1(list) para generar los desarreglos, que a su vez usaba permute3(list) para generar permutaciones.
Para obtener la lista dnk de elementos pendientes de insertar en los huecos "?", en lugar de usar el bucle que itera por dnkprev podemos usar dos alternativas que aparecen comentadas en el código anterior antes de ese bucle:
- Usar
let dnk = dnkprev.filter(v => v!=="") - Usar
let dnk = list.filter(v => !subresult.includes(v))en cuyo caso no es necesario usar las sentencias que manejen la variablednkprev
Eso no mejorá el coste, pero quizás resulte más eficiente. En cualquier caso he preferido dejarlo como está a fin de contar más fácilmente las iteraciones.
Analicemos ahora el coste:
- m = Max(0, n-k), aunque es de esperar que n≥k, hacemos esto para dar posibilidad de los casos n<k, en cuyo caso el número de desarreglos es cero, pero el algoritmo ejecutará algunas iteraciones.
- 1+n+Tc(n, k)+m+Td(m), pues antes de entrar en el primer bucle encontramos un
iter += 1, uniter += npara construir la listalistn, el coste Tc(n, k) de ejecutarcombine2(listn, k), uniter += mpara construir la listalistmy el coste Td(m) de ejecutarderange1(listm). - !m × pues el primer bucle tiene esa logitud que el número de desarreglos de la lista
listmal ejecutarderange1(listm), multiplicándose por lo que viene a continuación.- 1 + C(n, k) × sumando 1 antes de entrar al segundo bucle, que tiene una longitud de las combinaciones C(n, k) al ejecutar
combine2(listn, k), multiplicándose por lo que viene a continuación.- 1+n+n+k+n+n = 1+4n+k sólo basta observar el código para revelar que las distintas partes tienen una longitud n a excepción del bucle que itera por una combinación
for (let j=0; j<c[p].length; j++)que tiene una longitud k pues esa es la longitud de una combinación.
- 1+n+n+k+n+n = 1+4n+k sólo basta observar el código para revelar que las distintas partes tienen una longitud n a excepción del bucle que itera por una combinación
- 1 + C(n, k) × sumando 1 antes de entrar al segundo bucle, que tiene una longitud de las combinaciones C(n, k) al ejecutar
El algoritmo para generar combinaciones tiene el coste visto en combine2(n, k)
Y el que genera desarreglos con derange1(m) tiene este coste
Que a su vez usa este que genera permutaciones permute3(m)
| Tp(m) = m m! + 2 m! - 1 + 2 ∑j=2..m | m! |
| j! |
En caso de coste con copia se agregará lo resaltado en amarillo.
Unificando todo tenemos esta fórmula general que es igual que el contaje de iteraciones en el algoritmo derangeP1(list, k) para generar desarreglos parciales:
T(n, k) = 1 + n + m + Tc(n, k) + Td(m) + !m (1 + C(n, k) (1+4n+k))
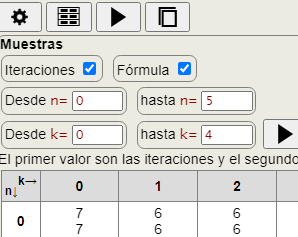
En la aplicación Combine Tools he agregado una nueva funcionalidad para verificar que las fórmulas del coste coinciden con el contaje de iteraciones, como se observa en la Figura.
Se generará una tabla con dos valores en cada celda, donde el primero es el contaje de iteraciones y el segundo el valor calculado según la fórmula, debiendo ser ambos iguales, como se comprueba para este algoritmo derangeP1(list, k) con esa fórmula obtenida.
| n↓k→ | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | 7 7 | 6 6 | 6 6 | 6 6 | 6 6 |
| 1 | 8 8 | 15 15 | 7 7 | 7 7 | 7 7 |
| 2 | 27 27 | 13 13 | 23 23 | 8 8 | 8 8 |
| 3 | 75 75 | 67 67 | 20 20 | 31 31 | 9 9 |
| 4 | 345 345 | 202 202 | 152 152 | 29 29 | 39 39 |
| 5 | 1923 1923 | 1193 1193 | 539 539 | 299 299 | 40 40 |