Desarreglos
Desarreglos
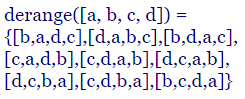
Los desarreglos (derangement) de una lista con n elementos distintos son todas las sublistas ordenadas con n elementos distintos que se pueden generar de tal forma que ninguno aparece en su posición original. Se denota como D(n). Y también como !n, el subfactorial de n.
Una permutación de n elementos tiene uno o más elementos que son puntos fijos si esos elementos se mantienen en su posición original. Desde esta definición un desarreglo es una permutación que no tiene ningún punto fijo.
Los primeros ejemplos hasta n=4 de desarreglos son:
| List | n | Result | D(n) |
|---|---|---|---|
| [] | 0 | {[]} | 1 |
| [a] | 1 | {} | 0 |
| [a, b] | 2 | {[b, a]} | 1 |
| [a, b, c] | 3 | {[c, a, b], [b, c, a]} | 2 |
| [a, b, c, d] | 4 | {[b,a,d,c],[d,a,b,c],[b,d,a,c],[c,a,d,b],[c,d,a,b],[d,c,a,b],[d,c,b,a],[c,d,b,a],[b,c,d,a]} | 9 |
Los distintos resultados se presentan como un Array entre corchetes como [c, a, b], lo que viene a ser una lista, pues el orden si importa. En cambio el conjunto total de resultados se encierra en llaves { }, pues se trata de un conjunto, donde el orden no importa.
Para la lista inicial con n=1 elemento [a] no hay ninguna permutación, pues la única es igual que la lista inicial y su elemento ocuparía la misma posición inicial, así que produce {} que contiene cero resultados.
Para la lista inicial con n=2 elementos [a, b] solo hay una forma de producir una permutación donde sus elementos no ocupen la posición inicial, y es {[b, a]} produciendo 1 resultado.
Sin embargo parece extraño que para una lista inicial con n=0 elementos [] produzca una permutación vacía {[]}, con lo que se produce 1 resultado. Pero vemos que se cumple el principio de que ningún elemento de las permutaciones de la lista final ocupa la misma posición que en la lista inicial, pues la única lista final está vacía al igual que la inicial.
El número de desarreglos de una lista con n elementos obedece a la siguiente recurrencia:
| D(n) = { | 1 | n=0 |
| 0 | n=1 | |
| (n-1) (D(n-1) + D(n-2)) | n≥2 |
De forma compacta podemos poner la recurrencia así:
!1 = 0,
!n = (n-1) !(n-1) + (n-1) !(n-2)
Se observa en WolframAlpha que la solución es D(n) = !n (el subfactorial de n). Intentemos llegar a esa solución aplicando la función generadora exponencial a esa recurrencia:
| G(x) = ∑n≥0 D(n) | xn |
| n! |
Las condiciones iniciales son las dos existentes, pues ambas intervienen en la recurrencia dados los términos D(n-1) y D(n-2):
| G0(x) = ∑n=0..0 D(n) | xn | = D(0) | x0 | = 1 |
| n! | 0! |
| G1(x) = ∑n=1..1 D(n) | xn | = D(1) | x1 | = 0 |
| n! | 1! |
Desplazamos 2 índices en la recurrencia para evitar negativos:
quedando
Multiplicamos ambos lados por 1/(n+1)
Apliquemos la función generadora a la recurrencia:
| ∑n≥0 | D(n+2) | xn | = ∑n≥0 D(n+1) | xn | + ∑n≥0 D(n) | xn |
| n+1 | n! | n! | n! |
Esta expresión es parecida a la que vimos para calcular los números de Fibonacci que era ∑n≥0 F(n+2) xn = ∑n≥0 F(n+1) xn + ∑n≥0 F(n) xn, que habíamos resuelto ajustando índices de los sumatorios. Sin embargo ahora tenemos un n! dividiendo que complica las cosas. Intentemos desde otra perspectiva, empezando por el término de la izquierda:
| ∑n≥0 | D(n+2) | xn | = ∑n≥0 D(n+2) | xn | = |
| n+1 | n! | (n+1)! |
| = ∑n≥0 D(n+2) | xn+1 x-1 | = | 1 | ∑n≥0 D(n+2) | xn+1 | = | 1 | ∑n≥1 D(n+1) | xn | = |
| (n+1)! | x | (n+1)! | x | n! |
| = | 1 | ( - D(1) | x0 | + ∑n≥0 D(n+1) | xn | ) = | 1 | ( - 0 + ∑n≥0 D(n+1) | xn | ) = |
| x | 0! | n! | x | n! |
| = | 1 | ∑n≥0 D(n+1) | xn |
| x | n! |
Sustituyendo esto en [2] y viendo que el término de la derecha es G(x) nos queda:
| 1 | ∑n≥0 D(n+1) | xn | = ∑n≥0 D(n+1) | xn | + G(x) |
| x | n! | n! |
Que tras agrupar los sumatorios nos queda:
| 1-x | ∑n≥0 D(n+1) | xn | = G(x) |
| x | n! |
El siguiente paso es identificar ese sumatorio. Para ello recordamos lo que vimos en derivadas e integrales de una serie en un tema anterior y que volvemos a repetir. Sin demostrarlo se presentan las siguientes identidades, siendo A(x) la función generadora de la serie ∑n≥0 an xn, donde A'(x) es su derivada:
- A'(x) = ∑n≥0 (n+1) an+1 xn
- x A'(x) = ∑n≥1 n an xn
- ∫ A(x) dx = ∑n≥1 (an-1 / n) xn
Para hacer uso de la primera identidad modificamos la apariencia del sumatorio en [3]:
| ∑n≥0 D(n+1) | xn | = ∑n≥0 (n+1) | D(n+1) | xn | = G'(x) |
| n! | (n+1)! |
Hemos identificado G'(x), pues si an = D(n)/n! entonces aquí tenemos exactamente lo que nos pide la primera identidad (n+1) an+1 = (n+1) D(n+1)/(n+1)! y el resultado es A'(x), que denominaremos G'(x). Por lo tanto [3] queda así:
| 1-x | G'(x) = G(x) |
| x |
que podemos poner así:
| G'(x) | = | x |
| G(x) | 1-x |
Esto es una ecuación diferencial lineal ordinaria con coeficientes variables de primer orden, homogénea en este caso. Se resuelve integrando en ambos lados:
| ∫ | G'(x) | dx = ∫ | x | dx |
| G(x) | 1-x |
Es obvio que la integral de la parte izquierda es:
Y la de la parte derecha es
Con lo que [5] queda así:
Agrupando logaritmos y constantes (pues en cualquier caso c2-c1 es una constante), aunque en otro apartado volveremos sobre esto:
Aplicando exponenciales en ambos lados y actuando otra vez sobre la constante
Despejamos
| G(x) = c | e-x |
| 1-x |
Vamos a prescindir de la constante que vale 1, pero lo calcularemos en otro apartado como dijimos antes.
Con lo que finalmente tenemos la función generadora de la recurrencia que calcula el valor numérico de los desarreglos equivalente a la serie G(x) = ∑n≥0 D(n) xn/n! = ∑n≥0 !n xn/n!
| G(x) = | e-x |
| 1-x |
La página OEIS, que trata la secuencia de valores de los desarreglos, vemos que la función generadora exponencial o E.g.f coincide con esa.
El subfactorial
En este apartado vamos a intentar obtener su serie y el término general de la función generadora [6]. Esa solución será la que cuenta el número de desarreglos de una lista con n elementos y que se denomina subfactorial.
Primero recordamos que en un apartado de un tema anterior que trataba sobre el producto de series, de Cauchy o convolución, donde trabajábamos con una recurrencia con coeficientes variables que denominábamos K-Tuplas, habíamos obtenido una función generadora exponencial parecida a esa:
| G(x) = | ex |
| 1-x |
Vea que sólo cambia el signo negativo del exponente. En ese tema obtuvimos la solución usando el producto de series. Aquí haremos lo mismo. Sean estas dos funciones:
| A(x) = | 1 | = ∑n≥0 xn |
| 1-x |
| B(x) = e-x = ∑n≥0 | (-x)n | = ∑n≥0 | (-1)n xn |
| n! | n! |
Vea que si ex = ∑n≥0 xn/n! entonces es obvio que e-x = ∑n≥0 (-x)n/n!
Entonces si G(x) = A(x) B(x), siendo aj = 1 y bj = (-1) j/j! solo tenemos que obtener el producto de esas series para obtener la solución. Se aplica el producto de series (de Cauchy o convolución):
Entonces siendo aj = 1 y bn-j = (-1)n/(n-j)!
| G(x) = A(x) B(x) = ( ∑n≥0 xn ) × ( ∑n≥0 | (-1)n xn | )= |
| n! |
| = ∑n≥0 ( ∑j=0..n | (-1)n-j | ) xn |
| (n-j)! |
Como para el rango n=0..j sucede esto (podemos hacer lo mismo que en ese enlace del tema anterior desplegando ambas sumas, o bien verificarlo en WolframAlpha):
| ∑j=0..n | (-1)n-j | = ∑j=0..n | (-1) j |
| (n-j)! | j! |
Entonces nos queda así, introduciendo n! para equipararlo a la función generadora:
| e-x | = ∑n≥0 ( ∑j=0..n | (-1) j n! | ) | xn | = ∑n≥0 !n | xn |
| 1-x | j! | n! | n! |
Asi que el término general que nos da la solución de la recurrencia que calcula el valor numérico de los desarreglos es esta fórmula que se designa como subfactorial:
| D(n) = !n = ∑j=0..n | (-1) j n! |
| j! |
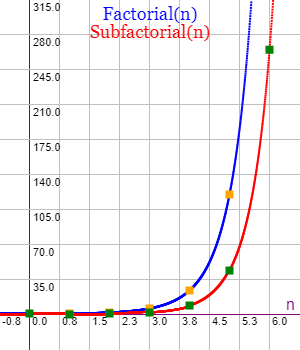
En la Figura puede ver la representación gráfica del subfactorial en rojo frente al factorial en azul. Puede visualizarlo en la herramienta Gráficas matemáticas usando esta definición de texto, para importar en la pestaña I/O de ese graficador.
Los valores del subfactorial se obtienen aplicando la fórmula [7]. Y aunque es válida solo para enteros no negativos, la gráfica pinta más puntos intermedios con objeto de visualizar la tendencia.
Los puntos de color diferente indican los valores enteros de n. Se observa que el subfactorial se mantiene por debajo del factorial, pues como dijimos, sólo computa las permutaciones sin puntos fijos, es decir, permutaciones donde sus elementos no ocupan sus posiciones iniciales.
Podemos expresar [7] de otra forma usando el concepto de función gamma incompleta:
| Γ(n, x) = (n-1)! e-x ∑j=0..n-1 | xj |
| j! |
Particularizando para n+1 y x = -1:
| Γ(n+1, -1) = n! e ∑j=0..n | (-1) j |
| j! |
Por lo tanto tenemos otra forma de presentar el subfactorial:
| D(n) = !n = | Γ(n+1, -1) |
| e |
Como vemos en la página de Wikipedia, hay otra expresión también pero para n≥1, donde [x] es el redondeo al entero más cercano:
| D(n) = !n = [ | n! | ] |
| e |
Y otra solución para calcular el subfactorial para n≥1:
Además de la recurrencia que vimos
!1 = 0,
!n = (n-1) !(n-1) + (n-1) !(n-2)
también esa página expone esta otra recurrencia alternativa:
!n = n !(n-1) + (-1)n
Podemos probar esto, que es lo mismo que D(n) = n D(n-1) + (-1)n, a partir de [7]:
Calculando la constante de la función generadora
Resolvimos la recurrencia siguiente con una función generadora:
En [6] obtuvimos la función generadora, pero habíamos prescindido temporalmente de una constante (dándole el valor 1 como un supuesto). Más bien era una suma de constantes de tal forma que c = c1 + c2, por lo que la función debería ser así:
| G(x) = (c1 + c2) | e-x |
| 1-x |
Se trata de obtenter esas constantes. Tras obtener la serie en el apartado anterior, tenemos esto incluyendo las constantes:
| G(x) = (c1 + c2) ∑n≥0 ( ∑j=0..n | (-1) j n! | ) | xn |
| j! | n! |
Como una de las condiciones iniciales era G0(x) = 1 entonces
| 1 = G0(x) = (c1 + c2) ∑n=0..0 ( ∑j=0..n | (-1) j n! | ) | xn | = |
| j! | n! |
| = (c1 + c2) ∑j=0..0 | (-1) j 0! | x0 | = (c1 + c2) | (-1)0 | = (c1 + c2) | |
| j! | 0! | 0! |
La suma es c = c1 + c2 = 1 tal como habíamos supuesto, por lo que en principio no necesitamos nada más. Pero veamos si se cumple la segunda condición G1(x) = 0
| 0 = G1(x) = (c1 + c2) ∑n=1..1 ( ∑j=0..n | (-1) j n! | ) | xn | = |
| j! | n! |
| = (c1 + c2) ( ∑j=0..1 | (-1) j 1! | ) | x1 | = (c1 + c2) 0 x |
| j! | 1! |
Esta segunda condición será cero independientemente de las constantes, con lo que sólo nos queda la primera condición que ha de ser c = c1 + c2 = 1, tal como habíamos supuesto.
Primer algoritmo para obtener desarreglos derange1(list)
El primer algoritmo para obtener los desarreglos lo planteamos a partir de las permutaciones quitando aquellas que tengan puntos fijos:
function derange1(list=[]){
//iter += 1;
let result = [];
let p = permute3(list);
for (let res of p){
//iter += 1;
/* if (res.every((v, i) => v!==list[i])){
result.push(res);
}*/
let ok = true;
for (let i=0; i<res.length; i++) {
//iter += 1;
if (res[i]===list[i]) {
ok = false;
break;
}
}
if (ok) result.push(res);
}
return result;
}Utilizamos el algoritmo permute3(list) que vimos en Permutaciones de Heap. Como se observa en el código sin comentar, primero obtenemos todas las permutaciones. Luego iteramos por ellas seleccionando aquellas que no tienen puntos fijos, es decir, donde no se produzca la coincidencia res[i]===list[i] que indica que el elemento en la permutación ocupa la misma posición que en la lista inicial.
Podemos definir matemáticamente este algoritmo como el siguiente conjunto:
Usamos el bucle interno para contar las iteraciones, lo que hacemos con las sentencias iter += ..., pero a efectos de una implementación más eficiente lo reemplazaríamos por el trozo de código comentado:
if (res.every((v, i) => v!==list[i])){
result.push(res);
}Veamos el coste de este algoritmo siendo n el tamaño de la lista inicial:
- +1 de entrada al algoritmo.
- +Tp que es el coste del algoritmo
permute3(list)y que tal como vimos en ese tema era (coste sin copiar resultados parciales):Tp(n) = 2n! - 1 + 2 ∑j=2..n n! j! Y con coste de copiar resultados parciales había que sumar n n!.
Tp(n) = n n! + 2n! - 1 + 2 ∑j=2..n n! j! - +n! por cada iteración del bucle externo, sumando +1 resulta en total del bucle con longitud n! que es el total de permutaciones en
p. - +(!n n + S(n)), pues por cada iteración del bucle externo tenemos +1 por cada iteración del bucle interno, teniendo este bucle una longitud que será máxima cuando la permutación sea un desarreglo sin puntos fijos, que sucede en !n veces, pues en esos casos deberá recorrerse todo el bucle interno cuya longitud es n (el tamaño de una permutación
res) y resultando !n n. Designamos S(n) la suma del restos de los casos donde se recorrerá n o menos elementos en permutaciones con uno o más puntos fijos.
Por lo tanto nos queda:
Sólo falta resolver para S(n), que podemos definir como suma de todas las posiciones del primer punto fijo en cada permutación con uno o más puntos fijos para las permutaciones de n elementos. Veamos varios ejemplos:
P(0)-D(0) = ∅
0
S(0) = 0
P(1)-D(1) = ∅
1
S(1) = 1
P(2)-D(2) = ab
1
S(2) = 1
P(3)-D(3) = abc bac acb cba
1 3 1 2
S(3) = 7
P(4)-D(4) = abcd abdc acbd acdb adbc adcb bacd bcad bdca cabd cbad cbda dacb dbac dbca
1 1 1 1 1 1 3 4 3 4 2 2 3 2 2
S(4) = 31
P(5)-D(5) = abcde abced abdce abdec abecd abedc acbde acbed acdbe acdeb acebd acedb adbce
1 1 1 1 1 1 1 1 1 1 1 1 1
adbec adcbe adceb adebc adecb aebcd aebdc aecbd aecdb aedbc aedcb bacde baced
1 1 1 1 1 1 1 1 1 1 1 3 3
badce baedc bcade bcdae bceda bdace bdcae bdcea beadc becad becda cabde cadbe
5 4 4 5 4 5 3 3 4 3 3 4 5
caedb cbade cbaed cbdae cbdea cbead cbeda cdabe cdbae ceadb cebda dabce dacbe
4 2 2 2 2 2 2 5 5 4 4 5 3
daceb dbace dbaec dbcae dbcea dbeac dbeca dcabe dcbae decab decba eabdc eacbd
3 2 2 2 2 2 2 5 5 3 3 4 3
eacdb ebacd ebadc ebcad ebcda ebdac ebdca ecadb ecbda edcab edcba
3 2 2 2 2 2 2 4 4 3 3
S(5) = 191
Se trata de usar la herramienta Combine Tools para obtener las permutaciones P(n) con, por ejemplo, permute3(list). Y los desarreglos D(n) con este algoritmo derange1(list). Manualmente quitamos de P(n) todas las permutaciones que estén en D(n), quedándonos el conjunto P(n)-D(n).
Tenemos entonces que P(n) - D(n) son las permutaciones con puntos fijos, que representamos de forma compacta. Anotamos en que posición se produce el primer punto fijo, pues es lo que hace el bucle interno del algoritmo, saliendo del mismo cuando encuentra el primer punto fijo. Sumamos todas esas anotaciones para cada n para obtener S(n). Se observa la secuencia 0, 1, 1, 7, 31, 191 que, con suerte, encontramos en OEIS que literalmente denomina:
"Smallest fixed point summed over all non-derangement permutations of {1,2,...,n}".
Podemos traducirlo como "El punto fijo más pequeño sumado sobre todas las permutaciones sin desarreglo de {1,2,...,n}". La traducción de "non-derangement permutations" con "permutaciones sin desarreglo" debería redactarse mejor como "permutaciones con puntos fijos" que se traduciría como "permutations with fixed points". En cualquier caso se están refiriendo a lo mismo, pues pone el ejemplo a(3) = 7 porque las permutaciones con puntos fijos de {1, 2, 3} son 123, 132, 213, 321 con los puntos fijos más pequeños 1, 1, 3, 2 (que suman 7). Y esto es lo mismo que obtuvimos contando los casos de P(3)-D(3). OEIS expone además estas dos soluciones equivalentes:
Son equivalentes, pues partiendo de la recurrencia !n = n !(n-1) + (-1)n que vimos en [11] tenemos lo siguiente incrementando un índice:
sustituyendo en [14] llegamos [13]:
Esa página de OEIS expone que obedece a la recurrencia siguiente:
Si la resolvemos con WolframAlpha obtenemos otra solución que, supuestamente, es equivalente:
Es esquivalente a las anteriores, pues tal como hicimos antes partiendo de la misma expresión !n = n !(n-1) + (-1)n que vimos en [11] particularizada para n+1:
sustituyendo en [15] obtenemos lo mismo que [14]:
Tras resolver S(n) volvemos al coste de nuestro algoritmo en [12], usando [14] para S(n):
Entonces tenemos la primera solución:
Usando [13] para S(n) obtenemos la segunda solución equivalente:
Y esta es la segunda solución equivalente para el coste de nuestro algoritmo que genera los desarreglos:
Coste de copia y análisis de iteraciones
El coste de copiar los resultados parciales queda integrado en Tp, dentro del algoritmo de permute3(list), que analizamos en un apartado del tema sobre el algoritmo de Heap.
...
if (n<=1) {
iter += 1;
if (withCopyCost) iter += list.length;
result.push(copy(list));
} else {
...En ciertos algoritmos tenemos que copiar el resultado parcial, pues en JavaScript los objetos se pasan por referencia en las llamadas a funciones. Pero para facilitar el análisis matemático de las recurrencias omitíamos el coste de copiar los resultados parciales, de tal forma que tras obtener la solución final agregábamos el coste de copia. En el caso del algoritmo de Heap el coste es n n! pues hay n! resultados parciales (permutaciones) cada uno con una longitud n.
Para analizar las iteraciones usamos Combine Tools, donde extraemos valores para los dos algoritmos permute3(list), basado en algoritmo de Heap, y derange1(list):
| n | permute3(list) | derange1(list) | ||||||
|---|---|---|---|---|---|---|---|---|
| n! | max Iter | Tp(n) | Iterp | !n | max Iter | T(n) | Iter | |
| 0 | 1 | 2×107 | 1 | 1 | 1 | 2×107 | 3 | 3 |
| 1 | 1 | 2×107 | 1 | 1 | 0 | 2×107 | 4 | 4 |
| 2 | 2 | 2×107 | 5 | 5 | 1 | 2×107 | 11 | 11 |
| 3 | 6 | 2×107 | 19 | 19 | 2 | 2×107 | 39 | 39 |
| 4 | 24 | 2×107 | 81 | 81 | 9 | 2×107 | 173 | 173 |
| 5 | 120 | 2×107 | 411 | 411 | 44 | 2×107 | 943 | 943 |
| 6 | 720 | 2×107 | 2473 | 2473 | 265 | 2×107 | 6115 | 6115 |
| 7 | 5040 | 2×107 | 17 319 | 17 319 | 1854 | 2×107 | 45 993 | 45 993 |
| 8 | 40 320 | 2×107 | 138 561 | 138 561 | 14 833 | 2×107 | 393 433 | 393 433 |
| 9 | 362 880 | 2×107 | 1 247 059 | 1 247 059 | 133 496 | 2×107 | 3 770 283 | 3 770 283 |
| 10 | 3 628 800 | 2×107 | 12 470 601 | 12 470 601 | 1 334 961 | 2×108 | 39 996 671 | 39 996 671 |
| 11 | 39 916 800 | 2×108 | 137 176 623 | CRASH | 14 684 570 | 2×108 | 465 195 613 | CRASH |
| 12 | 479 001 600 | 0 | 1 646 119 489 | - | 176 214 841 | 0 | 5 885 134 117 | - |
| 13 | 6 227 020 800 | 0 | 21 399 553 371 | - | 2 290 792 932 | 0 | 8 044 2971 391 | - |
La configuración de Combine Tool se establece por defecto en 20 millones de iteraciones (2×107), observando que el contaje de iteraciones Iter en el algoritmo coincide con el de las fórmulas T(n) para ambos hasta n=9.
Para n=10 hemos de incrementarlo a 200 millones (2×108) para poder obtener derange1. Con n=11 el navegador Chrome 119 sobre Windows 10 no lo soporta ocasionando un CRASH para ambos algoritmos. A partir de ahí se indican en color azul los valores de n!, !n así como los de las fórmulas T(n) de ambos algoritmos usando 2×107 o menos, incluso cero iteraciones, pues aunque no se complete el algoritmo nos devuelve esos valores calculados.