K-Tuplas
K-Tuplas
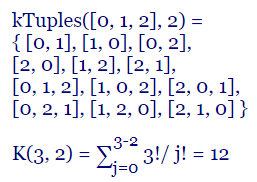
Definimos las K-Tuplas de un conjunto A con n elementos distintos a todas las sublistas ordenadas que podemos generar con las permutaciones aplicadas sobre todos los subconjuntos de orden k hasta n que se obtienen desde el conjunto A.
En el tema anterior vimos el caso particular con k=0, que nos sirvió como tema introductorio para ahora generalizarlo con valores superiores. Vimos un ejemplo de las K-Tuplas del conjunto A = {0, 1, 2} con k=0 que volvemos a repetir aquí pues es ilustrativo de las sublistas generadas:
[∅],
[0], [1], [2],
[0, 1], [1, 0], [0, 2], [2, 0], [1, 2], [2, 1],
[0, 1, 2], [1, 0, 2], [2, 0, 1], [0, 2, 1], [1, 2, 0], [2, 1, 0]
}
Se separan en líneas con el objetivo de ver lo siguiente: Los posibles subconjuntos de A se generan con C(n, k) usando el algoritmo combine(list, k) que usamos en la aplicación, iterando desde k=0 hasta k=n, incluyéndose el conjunto vacío ∅:
Para obtener las K(3, 0) K-Tuplas de A sólo tenemos que hallar las permutaciones de todos estos subconjuntos. Y su número es K(3, 0) = 16.
Para valores superiores de k las sublistas generadas son las de longitud k o superior. Así K(3, 1) son las anteriores a partir de las que tienen longitud 1, es decir, se quita la de longitud cero que es el conjunto vacío, K(3, 2) son las de orden 2 y superior y K(3, 2) son las de orden 3, que no es otra cosa que las permutaciones de {0, 1, 2}.
Para valores de k=0 hasta k=n=3 tenemos estos conjuntos de resultados que se ejecutan con el algoritmo kTuples(list, k) en la aplicación. Empecemos con k=0 donde tenemos K(3, 0) = 16 resultados:
Para k=1 tenemos K(3, 1) = 15 resultados:
Para k=2 tenemos K(3, 2) = 12 resultados (como se observa en la Figura):
Para k=3 tenemos K(3, 3) = 6 resultados, los mismos que P(3) = 3! = 6
Algoritmo para generar la K-Tuplas
Una generalización del algoritmo K-Tuplas puede establecerse así, donde k ∈ ℤ, k≥0:
// K(n, k) = n * K(n-1, k) + (n!/(n-k)!)
function K(n, k){
if (n<k){
return 0;
} else if (n===k) {
return factorial(k);
} else {
return n * K(n-1) + (factorial(n) / factorial(n-k));
}
}Esta sería la definición de la recurrencia para este algoritmo:
| K(n, k) = { | 0 | n<k |
| kk = k! | n=k | |
| n K(n-1, k) + nk | n>k |
Donde, tal como vimos en el tema anterior, el factorial descendente nk es:
| nk = | n! |
| (n-k)! |
De forma compacta la recurrencia de las K-Tuplas es así:
| K(n, k) = n K(n-1, k) + | n! |
| (n-k)! |
El caso base n=k es K(k, k) = kk = k! / (k-k)! = k!/0! = k! tal como se define el factorial descendente. Así que en general para cualquier n tenemos que K(n, n) = n! La similitud con las k-permutaciones o variaciones es obvia, dado que V(n, k) = P(n, k) = nk de tal forma que V(n, n) = P(n, n) = nn = n! también.
Vea que cuando k=0 entonces k0 = 1, teniendo la recurrencia que hemos visto en este tema en los apartados anteriores. La función generadora para esta nueva recurrencia es:
| G(x, k) = | xk ex |
| 1-x |
Cuando k=0 tenemos la serie ya vista G(x, 0) = ex / (1-x). La serie exponencial para esta recurrencia es:
| G(x, k) = | xk ex | = ∑n≥0 K(n, k) | xn |
| 1-x | n! |
donde K(n, k) es cualquiera de las siguientes pues son equivalentes (al final de este apartado veremos algunas más equivalentes):
Es obvio que podemos modificar en [2] el índice del sumatorio quedando como [3]. La siguiente tabla resume las ejecuciones en Wolfram Alpha (WA) para valores de 0 a 3. Las secuencias de 0 a 2 pueden observase en la página OEIS.
| k | Secuencia | ∑j=0..n-k n!/ j! | nk e Γ(n+1-k, 1) | nk 2F0(1, k-n; ; -1) | nk U(1, n+2-k, 1) |
|---|---|---|---|---|---|
| 0 | (OEIS) 1, 2, 5, 16, 65, 326 | WA | WA | WA | WA |
| 1 | (OEIS) 0, 1, 4, 15, 64, 325 | WA | WA | WA | WA |
| 2 | (OEIS) 0, 0, 2, 12, 60, 320, 1950 | WA | WA | WA | WA |
| 3 | 0, 0, 0, 6, 48, 300, 1920, 13650 | WA | WA | WA | WA |
Usando el despliegue de la recurrencia para hallar el término general de las K-Tuplas
Deduciremos K(n, k) usando la técnica del despliegue de la recurrencia para llegar a la solución K(n, k) = ∑j=0..n-k n!/j! vista en [2]. Iteramos desde n hasta el caso base k:
| = n (n-1)(n-2)···(k+1) k! + ∑j=0..n-(k+1) | n! |
| (n-j-k)! |
| = n! + ∑j=0..n-(k+1) | n! | = ∑j=0..n-k | n! |
| (n-j-k)! | (n-j-k)! |
Las partes en rojo son las recurrentes, observando que en i=k+1 tenemos ya el caso base K(k, k) = k! que nos permite resolver la recurrencia. Para deducir el sumatorio observamos que las iteraciones descendentes son i = n, n-1, n-2, ..., n-j+1, n-j, ..., k+1 con 1 ≤ j ≤ n-k, así que para la iteración i = n-j+1 tenemos el término j-ésimo del sumatorio:
| n(n-1)(n-2)···(n-j+1) (n-j)k = n(n-1)(n-2)···(n-j+1) | (n-j)! | = | n! |
| (n-j-k)! | (n-j-k)! |
El paso final es agregar n! dentro del sumatorio, dado que es como n!/0! y es el que corresponde al índice j=n-k.
Vea que los denominadores de cada sumando del sumatorio final anterior son los siguientes:
Mientras que para la solución K(n, k) = ∑j=0..n-k n!/j! vista en [2] los denominadores son los mismos aunque en orden inverso:
Por lo tanto el despliegue da como resultado la solución vista en [2] y, al mismo tiempo, tenemos otra solución equivalente (comprobar en Wolframalpha donde la resta resulta cero):
| K(n, k) = ∑j=0..n-k | n! |
| (n-j-k)! |
De esta es fácil deducir otra solución, que es la equivalente a la que obtuvimos con k=0 que expresa en que se basan las K-Tuplas, tal como expusimos en el tema anterior, en el apartado la función exponencial y las combinaciones K(n) = ∑j=0..n P(j) C(n, j):
Podemos cambiar el índice del sumatorio y ponerlo así:
Y también a partir de la misma deducimos otra que nos recuerda a la que obtuvimos para k=0 que era K(n) = ∑j=0..n n j usando el factorial descendente.
En [4], [5] y [6] presentamos soluciones equivalentes que tenían el factor nk. Podemos expresar también la solución ∑j=0..n-k n!/j! vista en [2] con este factor:
| K(n, k) = ∑j=0..n-k | n! | = | ∑j=0..n-k | (n-k)! | n! |
| j! | j! | (n-k)! |
Y por lo tanto con la definición del factorial descendente:
| K(n, k) = ∑j=0..n-k | (n-k)! nk |
| j! |
Función generadora de las K-Tuplas
Vamos a demostrar que la función generadora [1] se obtiene a partir de la serie exponencial aplicada al término general [2]:
| G(x, k) = | xk ex | = ∑n≥0 ( ∑j=0..n-k | n! | ) | xn |
| 1-x | j! | n! |
En el apartado producto de series del tema anterior vimos que G(x, 0) = ex / (1-x) se podía obtener multiplicando la serie exponencial con la geométrica, obteniéndose el término general K(n, 0) = ∑j=0..n n!/j!
| G(x, 0) = | ex | = ( ∑n≥0 | xn | ) × ( ∑n≥0 xn )= ∑n≥0 ( ∑j=0..n | n! | ) | xn |
| 1-x | n! | j! | n! |
Lo anterior se puede generalizar si multiplicamos la función por xk, lo que se puede comprobar en Wolframalpha
| G(x, k) = | xk ex | = ( ∑n≥0 | xn | ) × ( ∑n≥k xn ) |
| 1-x | n! |
Esta operación no es otra cosa que el producto de series o producto de Cauchy o convolución. Ahora sólo nos falta deducir el término general K(n, k). Vea que
Y que el producto anterior queda ahora así:
| G(x, k) = | xk ex | = ( ∑n≥0 | xn | ) × ( ∑n≥0 xn - ∑n=0..k-1 xn) = |
| 1-x | n! |
| = ( ∑n≥0 | xn | ) × ( ∑n≥0 xn ) - ( ∑n≥0 | xn | ) × ( ∑n=0..k-1 xn) |
| n! | n! |
| = G(x, 0) - ( ∑n≥0 | xn | ) × ( ∑n=0..k-1 xn) |
| n! |
Aquí tenemos dos productos de series, cuyo resultado igual que la función generadora G(x, k) puede comprobar en Wolframalpha. El primer producto es G(x, 0) = ex / (1-x) que hemos obtenido en el tema anterior en relación con el producto de series. Y sobre el segundo vemos que el multiplicando es una suma geométrica parcial:
| ∑n=0..k-1 xn = | 1-xk |
| 1-x |
Y por lo tanto ese producto es el siguiente, denotando como H(x, k) a esta parte:
| H(x, k) = ( ∑n≥0 | xn | ) × ( ∑n=0..k-1 xn) = | ex (1-xk) |
| n! | 1-x |
Así que la resta de ambos es precisamente G(x, k):
| G(x, k) = G(x, 0) - H(x, k) = | ex | - | ex (1-xk) | = ex ( | 1 | - | 1-xk | ) = | ex xk |
| 1-x | 1-x | 1-x | 1-x | 1-x |
Primer algoritmo para construir las K-Tuplas
En [7] vimos una solución equivalente para las K-Tuplas:
Vea que es igual que decir lo siguiente, lo que responde perfectamente a la definición de las K-Tuplas que vimos en el primer apartado de este tema:
Entonces haciendo uso de los algoritmos combine2(list, k) y permute2(list) podemos implementar el algoritmo para generar las K-Tuplas:
// K(n, k) = ∑j=k..n C(n, j) P(j)
function kTuples1(list, k=0){
iter += 1;
let result = [];
let n = list.length;
for (let j=k; j<=n; j++) {
iter += 1; // + cost combine2
let c = combine2(list, j);
for (let i=0; i<c.length; i++){
iter += 1 + j; // + cost permute2
result.push(...permute2(c[i]));
}
}
return result;
}El coste de este algoritmo (sin coste de copia) en función de los costes de combine2 y permute2 es el siguiente:
El coste que vimos en un tema anterior para generar combinaciones con el algoritmo combine2(n, k) que implementamos en la aplicación era:
El coste del algortimo permute2(n) lo veremos en un tema posterior permutar con Heap:
| TP2(n) = 1 + 2 n! ∑j=2..n | 1 |
| (n-j+1)! |
El coste con copia tiene la misma fórmula
pues se usarán los costes con copia correspondientes:
| T'P2(n) = n n! + 1 + 2 n! ∑j=2..n | 1 |
| (n-j+1)! |
Lo he denominado primer algoritmo por si pudiera encontrar otro segundo directo, es decir, sin hacer uso de algoritmos accesorios combine(list, k) o permute(list). Sin embargo no he podido encontrarlo.