30 may 2023

Convolución exponencial de factoriales y potencias

Convoluciones exponenciales de factoriales y potencias

*Figura*. Convolución exponencial de factoriales y potencias

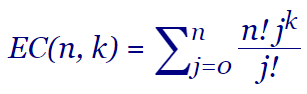
En la página OEIS podemos ver la secuencia 1, 6, 27, 124, 645, ... que denomina Convolución exponencial de factoriales y cuadrados (Exponential convolution of factorials and squares), con una referencia a Vladimir Reshetnikov. Es el resultado de la recurrencia a(n) = n a(n-1) + n² con a(0)=0. Expone entre otras la solución a(n) = ∑_j=0..n (n! j²) / j! que es como la que aparece en la Figura para k=2. Podemos encontrar OEIS con factoriales y cubos, que también se ajusta a la general con k=3.

Con un k ≥ 0 genérico podríamos estar hablando de convolución exponencial de factoriales y potencias que denominaré EC(n, k) (de Exponential Convolution). El asunto es demostrar que la solución general estimada de la Figura es correcta, tomando como partida la recurrencia para cualquier k ≥ 0 entero:

EC(n, k) = {	0	si n=0
EC(n, k) = {	n EC(n-1, k) + n^k	si n>0

Desarrollamos la recurrencia hasta llegar al caso base:

i=n ⇒ EC(n, k) = n EC(n-1, k) + n^k

i=n-1 ⇒ EC(n, k) = n ( (n-1) EC(n-2, k) + (n-1)^k ) + n^k =

= n(n-1) EC(n-2, k) + n(n-1)^k + n^k

i=n-2 ⇒ EC(n, k) = n(n-1) ( (n-2) EC(n-3, k) + (n-2)^k ) + n(n-1)^k + n^k

= n(n-1)(n-2) EC(n-3, k) + n(n-1)(n-2)^k + n(n-1)^k + n^k

i=2 ⇒ EC(n, k) = n(n-1)(n-2)···3 ( 2 EC(1, k) + 2^k ) +

+ n(n-1)···4·3^k + ... + n(n-1)(n-2)^k + n(n-1)^k + n^k =

= n(n-1)(n-2)···3·2 EC(1, k) + ∑_j=0..n-2 (n-j)^k (n!/(n-j)!)

i=1 ⇒ EC(n, k) = n(n-1)(n-2)···3·2 ( 1 EC(0, k) + 1^k ) +

+ ∑_j=0..n-2 (n-j)^k (n!/(n-j)!) =

= n(n-1)(n-2)···3·2·1 EC(0, k) + ∑_j=0..n-1 (n-j)^k (n!/(n-j)!)

= n(n-1)(n-2)···3·2·1·0 + ∑_j=0..n-1 (n-j)^k (n!/(n-j)!)

= 0 + ∑_j=0..n-1 (n-j)^k (n!/(n-j)!)

= ∑_j=0..n (n-j)^k (n!/(n-j)!)

Entonces


EC(n, k) = ∑_j=0..n	(n-j)^k n!
	(n-j)!

Vease que

(n-j)^k ∧ 0≤j≤n ⇒ n^k, (n-1)^k, ..., 1^k, 0^k

(n-j)! ∧ 0≤j≤n ⇒ n!, (n-1)!, ..., 1!, 0!

Mientras que

j^k ∧ 0≤j≤n ⇒ 0^k, 1^k, ..., (n-1)^k, n^k

j! ∧ 0≤j≤n ⇒ 0!, 1!, ..., (n-1)!, n!

Son los mismos términos aunque en orden inverso, por lo que podemos expresar la solución como


EC(n, k) = ∑_j=0..n	n! j^k
	j!

Similitud de estas convoluciones exponenciales con las K-Tuplas

En el tema anterior vimos la recurrencia de las K-Tuplas:

K(n, k) = {	0	si n<k
	k^k = k!	si n=k
	n K(n-1, k) + n^k	si n>k

Donde n^k es el factorial descendente:


n^k =	n!
	(n-k)!

La función generadora y una solución genral para las K-Tuplas era:


G(x, k) =	x^k e^x	= ∑_n≥0 K(n, k)	xⁿ
	1-x		n!

donde K(n, k) tenía esta solución (entre otras equivalentes):


K(n, k) = ∑_j=0..n-k	n!
	j!

Y la recurrencia de las convoluciones exponenciales de factoriales y potencias que estamos viendo en este tema es:

EC(n, k) = {	0	n=0
EC(n, k) = {	n EC(n-1, k) + n^k	n>0

con solución general que obtuvimos en el apartado anterior:


EC(n, k) = ∑_j=0..n	n! j^k
	j!

Hay una cierta similitud entre ambas recurrencias en la medida en que en una tenemos n^k y en la otra n^k. Y cierta similitud también en las soluciones. En los siguientes apartados analizaremos EC(n, k) para valores k = 0, 1, 2, 3, relacionándolo con las K-Tuplas.

Convolución exponencial de factoriales

Con k=0 tenemos que EC(n, 0) son las K-Tuplas K(n) o, lo que es lo mismo, las K-Tuplas generalizadas K(n, 0):


EC(n, 0) = ∑_j=0..n	n!	= K(n, 0) = K(n)
	j!

Con lo que resulta:

EC(n, 0) = K(n, 0)

La función generadora de EC(n, 0) es la misma que la de K(n, 0) al ser ambas iguales:


G_EC (x, 0) =	e^x
	1-x

Convolución exponencial de factoriales y potencias lineales

Con k=1 teniendo en cuenta que n! / (-1)! = 0 según se observa en Wolframalpha


EC(n, 1) = ∑_j=0..n	n! j	= ∑_j=0..n	n!	=	n!	+ ∑_j=1..n	n!	=
	j!		(j-1)!		(-1)!		(j-1)!


= 0 + ∑_j=1..n	n!	= ∑_j=1..n	n!	= ∑_j=0..n-1	n!	= K(n, 1)
	(j-1)!		(j-1)!		j!

Así que

EC(n, 1) = K(n, 1)

Vea que en el penúltimo paso podemos cambiar el índice a 0≤j≤n-1 precisamente porque n! / (-1)! = 0. En Wolframalpha se obtiene con ∑_j=0..n n! j / j! la misma secuencia 1, 4, 15, 64, 325, ... que vimos en la tabla de secuencias para K(n, 1). Puede comprobar que la resta de ambas expresiones resultan cero en Wolframalpha.

Podemos expresar EC(n, 1) también así, con lo que tenemos una recurrencia con respecto al valor de k anterior:

EC(n, 1) = EC(n, 0) - 1

observándose en Wolframalpha que se obtiene la misma secuencia 1, 4, 15, 64, 325, ... que también es la de K(n, 1) como dijimos antes.

No hay que confundir esa recurrencia con respecto a k con la del tema que es con respecto a n y que para k=1 es EC(n, 1) = n EC(n-1, 1) + n¹.

La función generadora se obtiene de la igualdad EC(n, 1) = K(n, 1) que vimos antes, siendo entonces la misma que la vista para las K-Tuplas K(n, 1):


G_EC (x, 1) =	x e^x
	1-x

También podríamos obtenerla de la expresión EC(n, 1) = EC(n, 0) - 1. Para ello aplicamos sumas exponenciales a cada término:


G_EC (x, 1) = ∑_n≥0 EC(n, 1)	xⁿ	=
	n!


= ∑_n≥0 EC(n, 0)	xⁿ	- ∑_n≥0	xⁿ	=
	n!		n!


= ∑_n≥0 K(n, 0)	xⁿ	- ∑_n≥0	xⁿ	=
	n!		n!


=	e^x	- e^x	=	x e^x
	1-x			1-x

Convolución exponencial de factoriales y cuadrados

Veamos ahora k=2


EC(n, 2) = ∑_j=0..n	n! j²	= ∑_j=0..n	n! j	= ∑_j=0..n	n! (j-1+1)	=
	j!		(j-1)!		(j-1)!


= ∑_j=0..n	n! (j-1)	+ ∑_j=0..n	n!	= ∑_j=0..n	n!	+ K(n, 1) =
	(j-1)!		(j-1)!		(j-2)!


=	n!	+	n!	+ ∑_j=2..n	n!	+ K(n, 1) =
	(-2)!		(-1)!		(j-2)!


= 0 + 0 + ∑_j=2..n	n!	+ K(n, 1) = ∑_j=0..n-2	n!	+ K(n, 1)
	(j-2)!		j!

Con lo que tenemos finalmente

EC(n, 2) = K(n, 2) + K(n, 1)

En Wolframalpha puede comprobar esto restando EC(n, 2) - K(n, 2) - K(n, 1) = 0 resulta cero. La secuencia que se obtiene es 1, 6, 27, 124, 645, ... que puede observarse en Wolframalpha. Vease que en el cuadro de secuencias teníamos K(n, 1) y K(n, 2), que si los sumamos término a término obtenemos esta secuencia:

n=	1	2	3	4	5
K(n, 1) =	1	4	15	64	325
K(n, 2) =	0	2	12	60	320
EC(n, 2) = K(n, 1) + K(n, 2) =	1	6	27	124	645

En la página OEIS puede comprobar esa secuencia 1, 6, 27, 124, 645, ..., obteniéndose la recurrencia a(n) = n a(n-1) + n², a(0) = 0 que es la misma que estamos usando para k=2. Se observa la misma solución general a(n) = ∑_k=0..n (n!/k!) k². Denomina a esa secuencia convolución exponencial de factoriales y cuadrados (Exponential convolution of factorials and squares), motivo por el cual he decidido usar ese nombre convoluciones exponenciales para este algoritmo.

Vease que podemos expresar EC(n, 2) también de esta forma:

EC(n, 2) = 2 EC(n, 1) - n

observándose en Wolframalpha que se obtiene la misma secuencia.

Recordemos que la función generadora de K(n, k) era:


G_K (x, k) =	x^k e^x
	1-x

Entonces si EC(n, 2) = K(n, 1) + K(n, 2) podemos obtener su función:


G_EC (x, 2) = G_K (x, 2) + G_K (x, 1) =	x² e^x	+	x e^x	=	(x²+x) e^x
	1-x		1-x		1-x

Entonces:


G_EC (x, 2) =	(x²+x) e^x
	1-x

Y esta es la misma que la observada en la página de OEIS comentada.

Si lo hacemos a partir de EC(n, 2) = 2 EC(n, 1) - n aplicando sumas y exponenciales a cada término y haciendo uso de G_EC (x, 1) que obtuvimos en el apartado anterior:


G_EC (x, 2) = ∑_n≥0 EC(n, 2)	xⁿ	=
	n!


= 2 ∑_n≥0 EC(n, 1)	xⁿ	- ∑_n≥0 n	xⁿ
	n!		n!


= 2 G_EC (x, 1) - ∑_n≥0 n	xⁿ	=
	n!


=	2 x e^x	- x e^x	=	(x²+x) e^x
	1-x			1-x

La última serie en el desarrollo anterior se resuelve así:


∑_n≥0 n	xⁿ	= ∑_n≥0	xⁿ	= ∑_n≥0	x^n-1 x	=
	n!		(n-1)!		(n-1)!


= x ∑_n≥0	x^n-1	= x ∑_n=-1..∞	xⁿ	=
	(n-1)!		n!


= x (	x^-1	+ ∑_n≥0	xⁿ	) =
	(-1)!		n!

= x ( 0 + e^x ) = x e^x

Obtenemos este resultado


∑_n≥0 n	xⁿ	= x e^x
	n!

donde hemos usado x^-1 / (-1)! = 0, como explicamos en el siguiente apartado, donde veremos que 1/(-n)! = 0 para n>0.

La función Gamma y 1/(-n)!

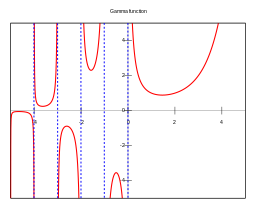
Para entender que 1/(-n)! = 0 con n>0 hemos de conocer el comportamiento de la Función Gamma, función que extiende los factoriales a los números reales y complejos. Se define de forma general como Γ(n) = (n-1)!, que se obtiene de su expresión como recursiva Γ(n) = (n-1) Γ(n-1).

En la página de Wikipedia sobre la Función Gamma se puede descargar la gráfica de la Figura, imagen original sin modificar cuya licencia se especifica.

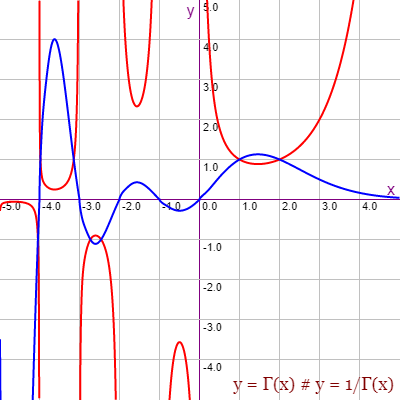
He podido también representar esa función como se observa en Figura, generada en mi aplicación Gráficas matemáticas. Usa la definición en formato de texto plot-gamma.txt, para lo cual debe copiar ese texto y pegarlo en la pestaña I/O para importarlo en ese graficador de funciones matemáticas si quisiera observar su generación.

La gráfica en color rojo coincide con la que se muestra en Wikipedia para la función Γ(x). En color azul se muestra la recíproca 1 / Γ(x).

En la parte positiva se observa en la gráfica roja que Γ(1) = 1, Γ(2) = 1, Γ(3) = 2 y, aunque no se observa, Γ(4) = 6. Es decir en los valores de x enteros positivos vemos que Γ(x) = (x-1)!. Observe como la gráfica azul coincide con la roja en la parte positiva en los puntos (1, 1) y (2, 1), valores correspondientes a Γ(1) = 1 y Γ(2) = 1 y al mismo tiempo a las recíprocas 1 / Γ(1) = 1 y 1 / Γ(2) = 1.

En cambio para cero y enteros negativos vemos que la gráfica roja toma valores ±∞. Mientras que la gráfica azul cruza exactamente por cero y los enteros negativos. Esto es un aspecto clave para resolver la duda de este apartado 1/(-n)! = 0 con n≥0, como veremos después.

Para graficar la función Gamma en los valores positivos podemos usar una aproximación como la que se expone en Wikipedia: Versions suitable for calculators:


Γ(x) ≈ √(	2π	) ( (	x	) √(	x sinh(	1	) +	1	) ) ^x

	x		e			x		810 x⁶

La recurrencia que vimos antes Γ(n) = (n-1) Γ(n-1) para enteros positivos puede extenderse a los reales con Γ(x) = (x-1) Γ(x-1), que también podemos expresar así Γ(x+1) = x Γ(x) o bien así Γ(x) = Γ(x+1) / x. Esta última nos permite extender la función para valores negativos y, por tanto, representarla gráficamente tal como explicamos en el despleglable siguiente.

Graficar función Gamma

Para graficar la función Gamma usando la función


Γ(x) ≈ √(	2π	) ( (	x	) √(	x sinh(	1	) +	1	) ) ^x

	x		e			x		810 x⁶

me he apoyado en parte en lo que expone una página de physics.uoguelph. Se trata de graficar recursivamente cada segmento entre dos enteros negativos. Preparamos cinco segmentos para cubrir el eje -5 < x ≤ 0.

Primer segmento -1< x ≤ 0: En la función en lugar de usar x usaremos x+1, de tal forma que si -1< x ≤ 0 ⇒ 0 < (x+1) ≤ 1 , con lo que la variable toma un valor mayor que cero y por tanto podemos aplicar la función que solo puede aplicarse para x > 0. El valor a obtener se divide entre x para obtener el valor correcto en el eje negativo, es decir, estaremos operando lo siguiente:


Γ(x) =	Γ(x+1)
	x

de donde se deduce que Γ(x+1) = x Γ(x) como ya sabemos.

Segundo segmento -2< x ≤ -1: Cambiamos ahora x por x+2, de tal forma que si -2< x ≤ -1 ⇒ 0 < (x+2) ≤ 1:


x Γ(x) = Γ(x+1) =	Γ(x+2)
	x+1

de donde


Γ(x) =	Γ(x+2)
	x(x+1)

Entonces usamos x+2 en la función y dividimos por x(x+1).

Tercer segmento -3< x ≤ -2: Cambiamos ahora x por x+3, de tal forma que si -3< x ≤ -2 ⇒ 0 < (x+3) ≤ 1. Vease que siempre usamos el segmento (0, 1] para calcular el valor de la función. Y luego al dividir por un polinomio en x recuperamos el valor correcto en el eje negativo:


Γ(x) =	Γ(x+3)
	x(x+1)(x+2)

Y así seguiríamos sucesivamente de forma recursiva cuántos segmentos necesitáramos para cubrir la gráfica negativa, en nuestro caso hasta cinco segmentos. Mi aplicación de gráficas matemáticas usa JavaScript básico (con limitaciones) para definir las funciones, siendo esta la parte que dibuja Γ(x) tanto para valores positivos como negativos:

if (x<=0) {
    v = (x>-1 && x<=0) ? 1 : 
        (x>-2 && x<=-1) ? 2 : 
        (x>-3 && x<=-2) ? 3 : 
        (x>-4 && x<=-3) ? 4 :
        5;
    u = x+v;
    w = (x>-1 && x<=0) ? x : 
        (x>-2 && x<=-1) ? x*(x+1) : 
        (x>-3 && x<=-2) ? x*(x+1)*(x+2) : 
        (x>-4 && x<=-3) ?  x*(x+1)*(x+2)*(x+3) :
        x*(x+1)*(x+2)*(x+3)*(x+4);
} else {
    u = x;
    w = 1;
}
color = 'red';
y = (sqrt(2*PI/u)*pow((u/E)*sqrt(u*sinh(1/u)+(1/(810*pow(u, 6)))), u))/w;

Básicamente la aplicación itera x por cada píxel horizontal de la pantalla y obtiene y, con lo que "pintará" ese punto (x, y) usando el recurso Canvas de JavaScript. El código JavaScript que puede incluir el usuario para definir las funciones es muy básico, debido a que he puesto varias limitaciones para usar JavaScript, pero se observa que ese código responde a la descripción dada.

La recíproca 1 / Γ(x) se obtiene de la misma forma, pues el valor resultante es simplemente al revés:


1	=	x
Γ(x)		Γ(x+1)


1	=	x(x+1)
Γ(x)		Γ(x+2)


1	=	x(x+1)(x+2)
Γ(x)		Γ(x+3)

y así sucesivamente.

Se observa en las gráficas que para enteros positivos está definida en todos los puntos, pero no para cero y los enteros negativos, como se ve que tiende a infinito en cada uno de esos puntos. Por lo tanto (-n)! → ±∞ para n≥0. Sin embargo como se expone al final del apartado de residuos de la Función Gamma de la página anterior, 1/Γ(z) es una función entera con ceros en z = 0, -1, -2, ... Entonces para n entero no negativo tenemos lo siguiente:


n≥0 ⇒	1	= 0
	Γ(-n)

Como Γ(n) = (n-1)! entonces Γ(-n+1) = (-n)! así que


n>0 ⇒	1	=	1	=0
	Γ(-n+1)		(-n)!

Mientras que para n=0 tenemos 1/(-0)! = 1/1 = 1 pues (-0)! = 1. Entonces podemos resumir que: (como se observa en Wikipedia)


1	,	1	,	1	,	1	... = 1, 0, 0, 0, ...
(-0)!		(-1)!		(-2)!		(-3)!

Un efecto adicional de lo anterior es el que exponemos en el siguiente desplegable, aunque nada tiene que ver con este apartado, puede ser intersante para usarlo en otros contextos.

Expresar una constante como una serie

Dicho sea de paso y aunque no tiene nada que ver con este tema, esto nos permite expresar una constante como una serie, donde a es un término constante respecto al índice j del sumatorio (ver en Wolframalpha):


∑_j=0..n	a	= a (1+0+0+0+...) = a
	(-j)!

Y si embebemos esta serie en una de potencias se obtiene la que representa la serie geométrica multiplicada por a (Wolframalpha):


∑_n≥0 ( ∑_j=0..n	a	) xⁿ	=	a
	(-j)!			1-x

Y si usamos la exponencial obtenemos, como era de esperar, lo siguiente: (Wolframalpha)


∑_n≥0 ( ∑_j=0..n	a	)	xⁿ	= a e^x
	(-j!)		n!

Una vez hecho este inciso en el tema, seguimos en el siguiente apartado con la convolución exponencial de factoriales y potencias.

Convolución exponencial de factoriales y cubos

Y ahora con k=3


EC(n, 3) = ∑_j=0..n	n! j³	= ∑_j=0..n	n! j²	=
	j!		(j-1)!


=	n! 0	+ ∑_j=1..n	n! j²	= 0 + ∑_j=0..n-1	n! (j+1)²	=
	(-1)!		(j-1)!		j!


= -	n! (n+1)²	+ ∑_j=0..n	n! (j+1)²	=
	n!		j!


= -(n+1)² + ∑_j=0..n	n! j²	+ ∑_j=0..n	n! 2 j	+ ∑_j=0..n	n!	=
	j!		j!		j!

= EC(n, 2) + 2 EC(n, 1) + EC(n, 0) - (n+1)² =

= ( K(n, 2) + K(n, 1) ) + 2 K(n, 1) + K(n, 0) - (n+1)² =

= K(n, 2) + 3 K(n, 1) + K(n, 0) - (n+1)²

Hemos aplicado n! 0 / (-1)! = 0 como puede comprobarse en Wolframalpha llegando a esta conclusión:

EC(n, 3) = K(n, 2) + 3 K(n, 1) + K(n, 0) - (n+1)²

Tomando datos de la tabla de secuencias de las K-Tuplas podemos obtener la secuencia resultante:

n=	0	1	2	3	4	5
K(n, 2) =	0	0	2	12	60	320
3 K(n, 1) =	0	3	12	45	192	975
K(n, 0) =	1	2	5	16	65	326
-(n+1)² =	-1	-4	-9	-16	-25	-36
EC(n, 3) = K(n, 2) + 3 K(n, 1) + K(n, 0) -(n+1)² =	0	1	10	57	292	1585

Vease que también EC(n, 3) es así:

EC(n, 3) = EC(n, 2) + 2 EC(n, 1) + EC(n, 0) - (n+1)²

Como EC(n, 2) = 2 EC(n, 1) - n entonces EC(n, 1) = ½ (EC(n, 2) + n). Y como por otro lado EC(n, 1) = EC(n, 0) - 1 entonces EC(n, 0) = EC(n, 1) + 1 = ½ (EC(n, 2) + n) + 1, entonces sustituyendo en lo anterior:

EC(n, 3) = EC(n, 2) + 2 (½ (EC(n, 2) + n)) + ½ (EC(n, 2) + n) + 1 - (n+1)² =

= EC(n, 2) + EC(n, 2) + n + ½ EC(n, 2) + ½ n + 1 - (n+1)² =

= (5/2) EC(n, 2) + n + ½ n + 1 - (n+1)² =

= (5/2) EC(n, 2) - (n²+n/2)

Entonces cabe esta forma recurrente con respecto a k anterior:

EC(n, 3) = (5/2) EC(n, 2) - (n²+n/2)

Si usamos la serie equivalente que obtuvimos en el desarrollo en el momento [3]


EC(n, 3) = ∑_j=0..n	n! j³	= ∑_j=0..n-1	n! (j+1)²
	j!		j!

podemos obtener con esta expresión una secuencia de esa serie en Wolframalpha, o bien usando la propia recurrencia en Wolframalpha, nos devuelve 1, 10, 57, 292, 1585, 9726, 68425, 547912, 4931937 para n≥1, que coincide con la anterior a partir de n=1.

En la página OEIS encontramos también esta secuencia denominándola Convolución exponencial de cubos y factoriales (Exponential convolution of cubes and factorial numbers). La recurrencia que expone es exactamente la misma que usamos a(0) = 0; a(n) = n a(n-1) + n³. Como solución expone la misma a(n) = ∑_j=0..n n! j³/j! que hemos usado. Expone como función generadora


G_EC (x, 3) =	(x³+3x²+x) e^x
	1-x

Podemos obtenerla a partir de [21] EC(n, 3) = K(n, 2) + 3 K(n, 1) + K(n, 0) - (n+1)², aplicando sumas y exponenciales a cada término, tras lo cual quedaría así:


G_EC (x, 3) = G_K (x, 2) + 3 G_K (x, 1) + G_K (x, 0) - ∑_n≥0	(n+1)² xⁿ	=
	n!


=	x² e^x	+ 3	x e^x	+	e^x	- e^x (x²+3x+1)	=
	1-x		1-x		1-x


=	e^x(x²+3x+1)	- e^x (x²+3x+1)	=
	1-x


= (x²+3x+1) e^x (	1	-1 )	=
	1-x


= (x²+3x+1) e^x (	x	)	=
	1-x


=	(x³+3x²+x) e^x
	1-x

Llegamos al resultado esperado resolviendo la serie implicada así:


∑_n≥0	(n+1)² xⁿ	= ∑_n≥0	n² xⁿ	+ 2 ∑_n≥0	n xⁿ	+ ∑_n≥0	xⁿ	=
	n!		n!		n!		n!

= (x²+x) e^x + 2 x e^x + e^x = (x²+3x+1) e^x

El primer término de la derecha en [6] se puede resolver así:


∑_n≥0	n² xⁿ	= ∑_n≥0	n xⁿ	= ∑_n≥0	n x^n-1 x	=
	n!		(n-1)!		(n-1)!


= x ∑_n≥0	n x^n-1	= x ∑_n=-1..∞	(n+1) xⁿ	=
	(n-1)!		n!


= x (	0 x^-1	+ ∑_n≥0	(n+1) xⁿ	) =
	(-1)!		n!


= x ( 0 + ∑_n≥0	n xⁿ	+ ∑_n≥0	xⁿ	) =
	n!		n!

= x (x e^x + e^x) = (x²+x) e^x

En [6] y [7] el término ∑_n≥0 n xⁿ / n! se resuelve aplicando el principio de derivadas de una serie. Si A(x) es la función generadora de la serie ∑_n≥0 a_n xⁿ entonces si A'(x) es la derivada de aquella función tenemos que x A'(x) = ∑_n≥1 n a_n xⁿ. Entonces si a_n = 1/n! y A(x) = ∑_n≥0 xⁿ/n! = e^x, con A'(x) = e^x entonces por ese principio:


∑_n≥0	n xⁿ	=	0 x⁰	+ ∑_n≥1	n xⁿ	= x e^x
	n!		0!		n!

Resumen de convoluciones exponenciales de factoriales y potencias

En la siguiente tabla se resume para valores k= 0, 1, 2, 3. La segunda columna nos da la equivalencia de EC(n, k) en función de K(n, k), las K-Tuplas que vimos en el tema anterior. En la tercera columna se expone la recurrencia de EC(n, k) en relación con EC(n, k-1). No hay que confundirla con la recurrencia respecto a n que define las convoluciones exponenciales y que es EC(n, k) = n EC(n-1, k) + n^k.

k	EC(n, k)			G(x, k)	Secuencia
0	∑_j=0..n n!/j!	K(n, 0)		e^x/(1-x)	(OEIS) 1, 2, 5, 16, 65, 326
1	∑_j=0..n n! j/j!	K(n, 1)	EC(n, 0) - 1	x e^x/(1-x)	(OEIS) 0, 1, 4, 15, 64, 325
2	∑_j=0..n n! j²/j!	K(n, 2) + K(n, 1)	2 EC(n, 1) - n	(x²+x) e^x/(1-x)	(OEIS) 1, 6, 27, 124, 645
3	∑_j=0..n n! j³/j!	K(n, 2) + 3 K(n, 1) + K(n, 0) - (n+1)²	(5/2) EC(n, 2) - (n²+n/2)	(x³+3x²+x) e^x/(1-x)	(OEIS) 1, 10, 57, 292, 1585

Serie y término general de la convolución exponencial de factoriales y potencias

Podemos suponer que el término general es de la forma:


EC(n, k) = ∑_j=0..n	n! j^k
	j!

Intentaremos demostrarlo a continuación.

La serie exponencial de factoriales que vimos en un tema anterior no es otra cosa que la serie geométrica, donde el término general es a_n = n!:


∑_n≥0 n!	xⁿ	= ∑_n≥0 xⁿ	=	1
	n!			1-x

Una serie exponencial de potencias k es de la forma


∑_n≥0 n^k	xⁿ
	n!

donde el término general es una potencia a_n = n^k. Si resolvemos para k = 0, 1, 2, 3 (puede comprobarlo en Wolframalpha para el valor k=3 por ejemplo):


∑_n≥0	n⁰ xⁿ	= e^x
	n!


∑_n≥0	n¹ xⁿ	= e^x x
	n!


∑_n≥0	n² xⁿ	= e^x (x²+x)
	n!


∑_n≥0	n³ xⁿ	= e^x (x³+3x²+x)
	n!

Ya vemos que el producto de las funciones en x de ambas series produce los resultados alcanzados en los apartados anteriores de forma indirecta usando las K-Tuplas. El producto, que también puede denominarse convolución, de las series [8] y [9] resulta


G(x, k) = ( ∑_n≥0 n!	xⁿ	) × ( ∑_n≥0 n^k	xⁿ	)	=
	n!		n!


= ( ∑_n≥0 xⁿ	) × ( ∑_n≥0	n^k	xⁿ	)
		n!

Recordamos el producto de series, de Cauchy o convolución que vimos en un tema anterior

A(x) B(x) = ( ∑_n≥0 a_n xⁿ ) × ( ∑_n≥0 b_n xⁿ ) = ∑_n≥0 ( ∑_j=0..n a_j b_n-j ) xⁿ

Entonces si tomamos a_n = n^k/n! que es el término general de la segunda serie en [10] y b_n = 1 que es el término general de la primera serie en [10] y como b_n-j = 1 para todo subíndice, tenemos


G(x, k) = ∑_n≥0 ( ∑_j=0..n	j^k	) xⁿ
	j!

Si multiplicamos y dividimos por n! para equipararlo con la exponencial tenemos finalmente la serie de la convolución exponencial de factoriales y potencias:


G(x, k) = ∑_n≥0 ( ∑_j=0..n	n! j^k	)	xⁿ
	j!		n!

Y confirmamos el término general que habíamos supuesto en el apartado anterior:


EC(n, k) = ∑_j=0..n	n! j^k
	j!

No parece que Wolfram Alpha resuelva [11] incluso particularizando k a un valor concreto. Pero si resuelve [10] aunque con valores concretos, por ejemplo, con k=3, lo que puede comprobarse en Wolframalpha, obteniendo (x³+3x²+x) e^x/(1-x) como se espera.

Resolviendo la recurrencia con la técnica de la función generadora exponencial

Como último ejercicio resolvermos la recurrencia directamente, al menos hasta llegar a obtener G(x, k):

EC(0, k) = 0

EC(n, k) = n EC(n-1, k) + n^k

La variable k se considera constante respecto a la recurrencia, puesto que no se modifica en cada llamada. Sumamos un índice para evitar negativos:

EC(n+1, k) = (n+1) EC(n, k) + (n+1)^k

Dividimos entre n+1:


EC(n+1, k)	= EC(n, k) + (n+1)^k-1
n+1

Aplicamos la funcion generadora exponencial:


G_n(x, k) = ∑_n≥0 EC(n, k)	xⁿ
	n!

La condición inicial es:


G₀(x, k) = ∑_n=0..0 EC(n, k)	xⁿ	= EC(0, k) = 0
	n!

Aplicamos xⁿ/n! a [12] y sumamos


∑_n≥0	EC(n+1, k)	xⁿ	= ∑_n≥0 EC(n, k)	xⁿ	+ ∑_n≥0 (n+1)^k-1	xⁿ
	(n+1)	n!		n!		n!

Veamos el término de la izquierda en [13]:


∑_n≥0	EC(n, k) xⁿ	= ∑_n=0..0	EC(n, k) xⁿ	+ ∑_n≥1	EC(n, k) xⁿ	=
	n!		n!		n!


=	EC(0, k) x⁰	+ ∑_n≥0	EC(n+1, k) xⁿ⁺¹	=
	0!		(n+1)!


= 0	+ x ∑_n≥0	EC(n+1, k) xⁿ	=
		(n+1) n!

Despejando obtenemos


∑_n≥0	EC(n+1, k) xⁿ	=	1	∑_n≥0	EC(n, k) xⁿ	=	G(x, k)
	(n+1) n!		x		n!		x

El primer término después del signo igual en [13] es G(x). Veamos el de la derecha:


∑_n≥0 (n+1)^k-1	xⁿ	= ∑_n≥0	(n+1)^k xⁿ	= ∑_n≥0	(n+1)^k xⁿ⁺¹ x^-1	=
	n!		(n+1)!		(n+1)!


=	1	∑_n≥0	(n+1)^k xⁿ⁺¹	=	1	∑_n≥1	n^k xⁿ	=
	x		(n+1)!		x		n!


=	1	( -	0^k x⁰	+ ∑_n≥0	n^k xⁿ	) =	1	∑_n≥0	n^k xⁿ	=
	x		0!		n!		x		n!


=	e^x P_k(x)
	x

Vemos que se obtiene la serie exponencial de potencias que vimos en [9] del apartado anterior ∑_n≥0 n^k xⁿ / n! Como vimos en ese apartado y aunque no obtuvimos una solución general para cualquier valor de k, si vimos valores para k = 0, 1, 2, 3 con los resultados e^x P_k(x), donde P_k(x) es un polinomio de orden k tal como vimos en ese apartado anterior, donde obtuvimos los primeros valores:

P₀(x) = 1

P₁(x) = x

P₂(x) = (x²+x)

P₃(x) = (x³+3x²+x)

Sustituyendo [14] y [15] en [13] queda lo siguiente:


G(x, k)	= G(x, k) +	e^x P_k(x)
x		x

obteniéndose:


G(x, k) =	e^x P_k(x)
	1-x

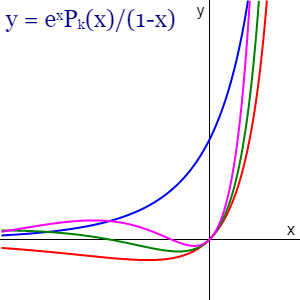
En la Figura se observa la representación gráfica para k = 0, 1, 2, 3, donde para k>0 todas las funciones pasan por el origen.

Puede usar la aplicación Gráficas matemáticas para generar esa representación usando la definición plot-exponential-convolution.txt, importándola en la pestaña I/O de esa herramienta.

Así que este resultado nos da la la función generadora genérica pero con el inconveniente de que no hemos encontrado un término general para P_k(x), pero si particularizamos para k = 0, 1, 2, 3 obtenemos las funciones esperadas:


G(x, 0) =	e^x
	1-x


G(x, 1) =	e^x x
	1-x


G(x, 2) =	e^x (x²+x)
	1-x


G(x, 3) =	e^x (x³+3x²+x)
	1-x