Variaciones
Variaciones sin repetición
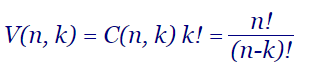
Las variaciones sin repetición de una lista con n elementos distintos son todas las sublistas ordenadas con k elementos distintos que se pueden extraer. Se denota como V(n, k). Las variaciones es un concepto que matemáticamente se considera como un caso particular de las permutaciones P(n, k) = n! / (n-k)!, denominadas como permutación parcial o k-permutación, con k≤n, siendo P(n, n) = n! / (n-n)! = n! Pero dado que aún sigue apareciendo como una figura distinta, mantenemos las variaciones en un apartado diferenciado de las permutaciones.
Por ejemplo, para la lista de elementos [a, b, c, d] las variaciones V(4, 2) es el conjunto de sublistas siguiente:
Observe que representamos las sublistas como Arrays, pues el orden si importa en este caso. Por ejemplo, un resultado es [a, b] que es distinto de [b, a]. El número de sublistas es V(4, 2) = 4!/(4-2)! = 4!/3! = 12.
Las variaciones sin repetición también pueden definirse como V(n, k) = C(n, k) × P(k), producto de combinaciones y permutaciones. Y es lo mismo que hablar de factorial descendente V(n, k) = nk tal como exponemos a continuación:
| V(n, k) = C(n, k) P(k) = C(n, k) k! = | n! | = |
| (n-k)! |
| = | n·(n-1)·(n-2)···(n-k+1)·(n-k)! | = |
| (n-k)! |
Algoritmo para generar variaciones vary1()
El primer algoritmo que usamos para generar las variaciones es muy simple, pues sigue la definición que vemos en la Figura:
| V(n, k) = C(n, k) P(k) = C(n, k) k! = | n! | k! = | n! |
| k! (n-k)! | (n-k)! |
Utilizando la parte resaltada y los algoritmos combine1(list, k) que vimos en el tema combinaciones sin repetición y permute1(list) que vimos en el tema permutaciones planteamos este algoritmo:
// V(n, k) = C(n, k) × P(k)
function vary1(list=[], k=0){
//iter += 1;
let result = [];
let c = combine1(list, k);
for (let res of c) {
//iter += 1;
result.push(...permute1(res));
}
return result;
}El coste de este algoritmo es el siguiente:
Donde el coste de las combinaciones del algoritmo combine1(list, k) era:
Y el coste de las permutaciones del algoritmo permute1(list) era:
| TP1(n) = Max ( 1, n! ( | n2+n-5 | + ∑j=3..n | j2+j+1 | ) ) |
| 2 | j! |
Algoritmo para generar variaciones vary2()
Otra posibilidad de generar variaciones es basándonos en el algoritmo que vimos en el tema combinaciones sin repetición, que se fundamenta en la identidad que sirve para construir el Triángulo de Pascal C(n, k) = C(n-1, k-1) + C(n-1, k), con lo que tenemos:
El algoritmo lo adaptamos así:
// V(n, k) = C(n, k) × P(k) = (C(n-1, k-1) + C(n-1, k)) × P(k)
function vary2(list=[], k=0, n=list.length, res=[], result=[],
n0=list.length){
if (k===0){
//iter += 1;
result.push(...permute1(res));
//} else if (n===0) {
//iter += 1;
} else if (n>0) {
//iter += 1;
res.push(list[n0-n]);
vary2(list, k-1, n-1, res, result);
res.pop();
vary2(list, k, n-1, res, result);
}
return result;
}El coste del algoritmo de combinaciones que vimos en el apartado con coste de copia era así:
El de este algoritmo es similar:
donde el coste de las TP1(k) es el del algoritmo permute1(list) que vimos en el tema permutaciones:
| TP1(n) = Max ( 1, n! ( | n2+n-5 | + ∑j=3..n | j2+j+1 | ) ) |
| 2 | j! |
Algoritmo para generar variaciones vary3()
Este algoritmo no mejora el coste de los anteriores, pero es un intento de conseguirlo sin utilizar otros algoritmos, como hacíamos antes.
// V(n, k) = n × V(n-1, k-1)
function vary3(list=[], k=0, k0=k){
let n = list.length;
let result = [];
if (k===1) {
if (k0===1) {
//iter += n;
result = list.map(v => [v]);
} else {
//iter += 1;
result = list;
}
} else if (k>1) {
//iter += 1;
for (let j=0; j<n; j++) {
//iter += n+1;
let listMinor = list.slice(0,j).concat(list.slice(j+1));
let subResult = vary3(listMinor, k-1, k0);
for (let i=0; i<subResult.length; i++){
//iter += subResult[i].length+1;
result.push([list[j], ...subResult[i]]);
}
}
}
return result;
}Es una aplicación del algoritmo permute1(list) que vimos en permutaciones (y también en el tema coste permutar) donde definíamos la recurrencia:
| T(n) = { | 1 | si n≤2 |
| n T(n-1) + n2 + n + 1 + n n! | si n>2 |
Recordando que las variaciones son
| V(n, k) = | n! |
| (n-k)! |
Entonces el término n n! lo sustituimos por k V(n, k), de tal forma que cuando k=n tendremos el término anterior. En la definición ahora tenemos que diferenciar estos casos según el valor k0 inicial:
- k0 = 0 ∨ n < k0 ⇒ T(n, k0) = 1
- 1 = k0 ≤ n ⇒ T(n, 1) = n
- 1 < k0 ≤ n ⇒
T(n, k) = { 1 k = 1 n T(n-1, k-1) + n2 + n + 1 + k V(n, k) k > 1
No tiene sentido hablar de variaciones con k0=0 o n < k0, o mejor dicho, el conjunto que se genera es un conjunto vacío, pero en todo caso el algoritmo ejecuta una iteración entrando en el recursivo la primera vez, por lo que el coste es T(n, k0) = 1. Vea que V(n, k) = n!/(n-k)! y que si n=0 ∧ k>0 o n < k entonces (n-k) < 0. Y ya vimos en la función Gamma y 1/(-n)! que 1/(-n)! = 0. De esa forma queda claro que V(n, k) = n!/(n-k)! = 0 cuando (n-k) < 0.
Para el caso 1 = k0 ≤ n el algoritmo fuerza T(n, 1) = n, pues es el coste del caso k0===1, cuando la primera llamada es con k0 = 1, donde hacíamos result = list.map(v => [v]), cuyo coste es la longitud n de la lista. Pero para la recurrencia tomaremos T(n, 1) = 1 pues consideramos que la primera llamada se produce con k0 > 1 y el caso base es ahora result = list cuyo coste es unitario.
Tenemos entonces esta recurrencia para el caso general con la que tenemos que calcular su coste:
Usaremos el despliegue de la recurrencia para obtener el término general. Denotemos temporalmente Q(n) = n2 + n + 1 y despleguemos la recurrencia desde la iteración n:
Iteración n-1:
El término resaltado en azul se resuelve así:
| n (k-1) V(n-1, k-1) = n (k-1) | (n-1)! | = (k-1) | n! | = (k-1) V(n, k) |
| ((n-1)-(k-1))! | (n-k)! |
Iteración n-2:
En este paso también hemos resuelto lo mismo que antes para el término en la misma posición:
| n(n-1)(k-2) V(n-2, k-2) = n(n-1)(k-2) | (n-2)! | = (k-2) | n! | = (k-2) V(n, k) |
| ((n-2)-(k-2))! | (n-k)! |
Seguimos sucesivamente hasta llegar a la iteración n-(k-2) = n-k+2, siendo la llamada recursiva siguiente como T(n-(k-2)-1, k-(k-2)-1) = T(n-k+1, 1) deduciendo ya finalmente la expresión final a partir de las secuencias que se evidencian en los pasos anteriores:
Simplificando:
La expresión de la primera línea anterior se reduce a esto pues T(n-k+1, 1) = 1 es el caso base:
| n(n-1)(n-2)···(n-k+2) T(n-k+1, 1) = n(n-1)(n-2)···(n-k+2) × 1 = | n! |
| (n-k+1)! |
La segunda línea queda así:
| = ∑j=n-k+2..n Q(j) | n! |
| j! |
Y la tercera línea así:
Agrupando todo nos queda:
| T(n, k) = | n! | + ∑j=n-k+2..n Q(j) | n! | + ∑j=2..k j V(n, k) |
| (n-k+1)! | j! |
Reponiendo Q(n) y V(n, k) tenemos:
| T(n, k) = | n! | + ∑j=n-k+2..n (j2+j+1) | n! | + ∑j=2..k j | n! |
| (n-k+1)! | j! | (n-k)! |
La suma del término ∑j=2..k j = 1/2 (k2+k-2), con lo que podemos simplificarlo así, siendo la fórmula final del coste con 1 < k ≤ n como sigue:
| T(n, k) = | n! | ( | 1 | + | k2+k-2 | ) + ∑j=n-k+2..n (j2+j+1) | n! |
| (n-k)! | n-k+1 | 2 | j! |
Recordemos que con 1 = k ≤ n el coste es T(n, 1) = n tal como explicamos en un párrafo anterior.
Y que con k=0 ∨ n<k el coste es T(n, k) = 1, puesto que no tiene sentido hablar de variaciones con k=0 o n < k, pero en todo caso el algoritmo ejecuta una iteración entrando en el recursivo la primera vez.
La siguiente tabla resume algunos valores de la definición anterior que también se obtienen contando iteraciones en el algoritmo dado:
| k | n | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 1 | 13 | 28 | 49 | 76 | 109 | 148 | 193 | 244 | 301 |
| 3 | 1 | 1 | 70 | 205 | 456 | 859 | 1450 | 2265 | 3340 | 4711 |
| 4 | 1 | 1 | 1 | 397 | 1536 | 4219 | 9430 | 18393 | 32575 | 53671 |
| 5 | 1 | 1 | 1 | 1 | 2616 | 12859 | 42190 | 109113 | 241228 | 477031 |
Vea que con k=1 forzamos el coste T(n, 1) = n.
Resolver usando otros medios
La definición de la recurrencia que vimos en el apartado anterior era así (para el caso de k0 > 1 que explicamos al inicio de ese apartado):
| T(n, k) = | { | 1 | k = 1 |
| n T(n-1, k-1) + n2 + n + 1 + k n!/(n-k)! | k > 1 |
Es una recurrencia con dos variables, que varía en las dos y el caso base es k=1. En principio no vamos a aplicar la técnica de la función generadora, intentando usar otros medios.
Supongamos que en el momento inicial tenemos que n0, k0 son los valores iniciales de n y k. Como ambas variables bajan de valor al mismo tiempo debido al término de la recurrencia T(n-1, k-1) entonces podemos poner la recurrencia sólo en términos de n.
Como la recurrencia se desplaza en k con los valores sucesivos k0, k0-1, k0-2,..., 3, 2, 1 se observa que en n los valores sucesivos son n0, n0-1, n0-2,..., n0- (k0-2), n0- (k0-1)
Si hacemos k = n - (n0 - k0) entonces en el momento inicial tendremos T(n0, k0) puesto que:
Y en el momento final T(n0-k0+1, 1) puesto que:
Además la diferencia n-k se mantiene constante:
Con esto podemos expresar la recurrencia en una única variable n:
| T(n) = | { | 1 | n = n0 - k0 + 1 |
| n T(n-1) + n2 + n + 1 + (n- (n0 - k0)) n!/(n0-k0)! | n > n0 - k0 + 1 |
Veamos la parte recurrente:
| T(n) = n T(n-1) + n2 + n + 1 + | (n- (n0 - k0)) | n! |
| (n0-k0)! |
Si denotamos b = n0-k0 entonces tenemos esta recurrencia:
| T(n) = | { | 1 | n = b + 1 |
| n T(n-1) + n2 + n + 1 + ((n-b)/b!) n! | n > b + 1 |
Para resolver esta recurrencia con una función generadora hay que tener en cuenta que tiene un caso base genérico variable según b, cuando usualmente resolvíamos recurrencias con casos bases particularizados a un número. Esto complica mucho los desarrollos para obtener la función generadora, como veremos en el tema siguiente que expone la resolución de recurrencias con caso base genérico.
Mientras tanto intentaremos resolverlo por otro medio, que denominaremos secuencia de casos bases y que explicaremos en el siguiente tema. Si particularizamos para los primeros valores de b = {0, 1, 2, 3, 4} tenemos estas definiciones:
Podríamos resolver estas recurrencias con la función generadora con objeto de ver si se deduce un término general para cualquier valor de b, pues son similares a la vista para las permutaciones que era T(n) = n T(n-1) + n2 + n + 1 + n n!, observando que es igual que la primera para b=0, aunque con caso base T(1) = 1. Pero nos apoyaremos en WolframAlpha que nos resuelve los casos anteriores como sigue:
Se observan estas secuencias de valores numéricos en lo anterior, que hemos completado con algunos términos más obtenidos también en WolframAlpha:
- 1/2, 1/2, 1/4, 1/12, 1/48, 1/240, 1/1440, 1/10080, 1/80640, ...
- 1, -1, -3, -5, -7, -9, -11, -13,- 15, ...
- -8, -16, -38, -122, -508, -2588, -15626, -109558, -876752, ...
En este enlace de WolframAlpha puede ver la solución del último caso b=4, aunque realmente la expresa así:
Recordemos que Γ(n+1) = n! y que tal como vimos en la función gamma incompleta
| Γ(n+1, 1) = n! e-1 ∑j=0..n | 1 |
| j! |
Y por lo tanto
| e Γ(n+1, 1) = ∑j=0..n | n! |
| j! |
En WolframAlpha se obtienen estos valores
| b=n-k | n | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| 0 | 1 | 13 | 70 | 397 | 2616 | 20059 | 175750 | 1728633 | 18823708 | |
| 1 | - | 1 | 28 | 205 | 1536 | 12859 | 120310 | 1244793 | 14106268 | |
| 2 | - | - | 1 | 49 | 456 | 4219 | 42190 | 458553 | 5397148 | |
| 3 | - | - | - | 1 | 76 | 859 | 9430 | 109113 | 1344988 | |
| 4 | - | - | - | - | 1 | 109 | 1450 | 18393 | 241228 | |
Los celdas con "-" son valores no aplicables, pues el caso base se fija en n = b+1, de tal forma por ejemplo que si b=4 entonces el caso base está en T(4+1) = T(5) = 1, como se observa en la última fila.
En las soluciones obtenidas antes en WolframAlpha se observa que se obtienen en horizontal para cada valor de b = n-k los mismos valores que en las diagonales que obtuvimos en el apartado anterior (obviando la primera fila pues en la definición forzamos que en ese caso el coste es n):
| k | n | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 2 | - | 13 | 28 | 49 | 76 | 109 | 148 | 193 | 244 | |
| 3 | - | - | 70 | 205 | 456 | 859 | 1450 | 2265 | 3340 | |
| 4 | - | - | - | 397 | 1536 | 4219 | 9430 | 18393 | 32575 | |
| 5 | - | - | - | - | 2616 | 12859 | 42190 | 109113 | 241228 | |
En las soluciones obtenidas de WolframAlpha podemos identificar las secuencias de valores numéricos, como la primera fracción con secuencia 1/2, 1/2, 1/4, 1/12, 1/48, 1/240, 1/1440, 1/10080, 1/80640, ..., cuyo término general es 1/(2 b!) para b≥0.
Y también la secuencia 1, -1, -3, -5, -7, -9, -11, -13, -15, ... = -2b+1 para b≥0. Por ahora dejamos pendiente la secuencia 8, 16, 38, 122, 508, 2588, 15626, 109558, 876752, ... que obedece a una función desconocida F(b), entonces la solución general sería así:
Esta sería la solución para T(n, b), en función de la diferencia b=n-k. Pero aún no es la solución general T(n, k) pues nos falta resolver F(b), cuya secuencia es 8, 16, 38, 122, 508, 2588, 15626, 109558, 876752, .... La expresión para generar esa secuencia es la siguiente, pudiendo ver como se deduce en el desplegable:
| F(b) = b - b2 + 8 ∑j=0..b | b! |
| j! |
Con lo que la solución sería esta:
| T(n, b) = | 1 | ( (n-2b+1)n-b+b2-8 ∑j=0..b | b! | ) n! | - (n+3) + 4 ∑j=0..n | n! |
| 2 b! | j! | j! |
Si deshacemos el cambio b = n-k obtenemos la solución general:
| T(n, k) = | 1 | ( (n-2(n-k)+1)n-(n-k)+(n-k)2-8 ∑j=0..(n-k) | (n-k)! | ) n! | - (n+3) + 4 ∑j=0..n | n! |
| 2 b! | j! | j! |
Simplificando una parte
y reagrupando algunas cosas nos queda esto:
| T(n, k) = | n! | ( | k2+k | - 4 ∑j=0..(n-k) | (n-k)! | ) - (n+3) + 4 ∑j=0..n | n! | = |
| (n-k)! | 2 | j! | j! |
| = | n! | ( | k2+k | ) - 4 ∑j=0..(n-k) | n! | - (n+3) + 4 ∑j=0..n | n! | = |
| (n-k)! | 2 | j! | j! |
| = | n! | ( | k2+k | ) - (n+3) + 4 (- ∑j=0..(n-k) | n! | + ∑j=0..n | n! | ) = |
| (n-k)! | 2 | j! | j! |
| = | n! | ( | k2+k | ) - (n+3) + 4 ∑j=n-k+1..n | n! |
| (n-k)! | 2 | j! |
Esta es la solución final
| T(n, k) = | n! | ( | k2+k | ) - (n+3) + 4 ∑j=n-k+1..n | n! |
| (n-k)! | 2 | j! |
Equiparando soluciones
Para equiparar soluciones [1] obtenida con la técnica del despliegue y [2] a partir de la definición de la recurrencia, partimos de esta segunda expresión y vamos ajustando cosas hasta tratar de igualar téminos de la otra expresión:
| T(n, k) = | n! | ( | k2+k | ) - (n+3) + 4 ∑j=n-k+1..n | n! | = |
| (n-k)! | 2 | j! |
| = | n! | ( | k2+k | ) - (n+3) + 4 ( | n! | + ∑j=n-k+2..n | n! | ) = |
| (n-k)! | 2 | (n-k+1)! | j! |
| = | n! | ( | k2+k | ) - (n+3) + | 4 n! | + 4 ∑j=n-k+2..n | n! | = |
| (n-k)! | 2 | (n-k+1)! | j! |
| = | n! | ( | k2+k | ) - (n+3) | + | n! | + | 3 n! | + 4 ∑j=n-k+2..n | n! | = |
| (n-k)! | 2 | (n-k+1) (n-k)! | (n-k+1)! | j! |
| = | n! | ( | 1 | + | k2+k | ) - (n+3) + | 3n! | + 4 ∑j=n-k+2..n | n! | = |
| (n-k)! | n-k+1 | 2 | (n-k+1)! | j! |
| = | n! | ( | 1 | + | k2+k | - | 2 | + 1) - (n+3) + | 3n! | + 4 ∑j=n-k+2..n | n! | = |
| (n-k)! | n-k+1 | 2 | 2 | (n-k+1)! | j! |
| = | n! | ( | 1 | + | k2+k-2 | + 1) - (n+3) + | 3n! | + 4 ∑j=n-k+2..n | n! | = |
| (n-k)! | n-k+1 | 2 | (n-k+1)! | j! |
| = | n! | ( | 1 | + | k2+k-2 | ) - (n+3) + | n! | + | 3n! | + 4 ∑j=n-k+2..n | n! | = |
| (n-k)! | n-k+1 | 2 | (n-k)! | (n-k+1)! | j! |
| = | n! | ( | 1 | + | k2+k-2 | ) - (n+3) + | (n-k+4) n! | + 4 ∑j=n-k+2..n | n! |
| (n-k)! | n-k+1 | 2 | (n-k+1)! | j! |
Si comprobamos esta expresión con [1] que reproducimos a continuación:
| T(n, k) = | n! | ( | 1 | + | k2+k-2 | ) + ∑j=n-k+2..n (j2+j+1) | n! |
| (n-k)! | n-k+1 | 2 | j! |
Observamos que para que ambas sean iguales tenemos que demostrar lo siguiente:
| - (n+3) + | (n-k+4) n! | + 4 ∑j=n-k+2..n | n! | = ∑j=n-k+2..n (j2+j+1) | n! |
| (n-k+1)! | j! | j! |
Que es lo mismo que demostrar la siguiente igualdad:
| ∑j=n-k+2..n (j2+j-3) | n! | = - (n+3) + | (n-k+4) n! |
| j! | (n-k+1)! |
En el tema del algoritmo para generar permutaciones, que sirve de base para el que usamos en este tema, vimos como equiparábamos soluciones también. Vimos la relación con las K-Tuplas y las Convoluciones exponenciales de factoriales y potencias. En este caso vamos a desarrollarlo directamente, sin que sea necesario el conocimiento de lo anterior, pero en el fondo los ajustes que hacemos en los rangos de los sumatorios se basan en los conceptos que expusimos en esos temas (se expone algo más en el último apartado de este tema).
Comenzamos con la parte izquierda de [3]:
| ∑j=n-k+2..n (j2+j-3) | n! | = A + B + C = |
| j! |
| = - 3 ∑j=n-k+2..n | n! | + ∑j=n-k+2..n j | n! | + ∑j=n-k+2..n j2 | n! |
| j! | j! | j! |
El primer término que denominaremos A lo dejaremos tal como está:
| A = - 3 ∑j=n-k+2..n | n! |
| j! |
Veamos el segundo término que denominaremos B
| B = ∑j=n-k+2..n j | n! | = ∑j=n-k+2..n | n! | = ∑j=n-k+1..n-1 | n! | = |
| j! | (j-1)! | j! |
| = - | n! | + | n! | + ∑j=n-k+2..n | n! | = |
| n! | (n-k+1)! | j! |
| = - 1 + | n! | + ∑j=n-k+2..n | n! |
| (n-k+1)! | j! |
Se observa que al final de la primera línea anterior hemos realizado un ajuste en el rango [n-k+1..n-1] con objeto de tener j! en el denominador de la fracción. En la segunda línea ajustamos otra vez el rango a [n-k+2..n] para que sea igual que el que tenemos en el primer sumando A de [4], para lo cual restamos el último término n!/n! y sumamos el primero n!/(n-k+1)!
Vamos ahora por el término de la derecha en [4] que denominaremos C:
| C = ∑j=n-k+2..n j2 | n! | = ∑j=n-k+2..n j | n! | = ∑j=n-k+1..n-1 (j-1+1) | n! | = |
| j! | (j-1)! | (j-1)! |
| = ∑j=n-k+2..n (j-1) | n! | + ∑j=n-k+2..n | n! | = ∑j=n-k+2..n (j-1) | n! | + B = |
| (j-1)! | (j-1)! | (j-1)! |
| = ∑j=n-k+2..n | n! | + B = ∑j=n-k..n-2 | n! | + B = |
| (j-2)! | j! |
| = - | n! | - | n! | + | n! | + | n! | + ∑j=n-k+2..n | n! | + B = |
| n! | (n-1)! | (n-k+1)! | (n-k)! | j! |
| = - 1 - n | + | n! | + | n! | + ( ∑j=n-k+2..n | n! | ) - 1 + | n! | + ∑j=n-k+2..n | n! | = |
| (n-k+1)! | (n-k)! | j! | (n-k+1)! | j! |
| = - 2 - n | + | 2 n! | + | n! | + 2 ∑j=n-k+2..n | n! |
| (n-k+1)! | (n-k)! | j! |
En la segunda línea sustituímos el segundo término por lo que ya obtuvimos en el paso anterior y que habíamos denominado B y que luego volveremos a reponer. En la tercera línea hacemos el ajuste [n-k..n-2] con objeto de tener j! en el denominador de la fracción. En la cuarta línea volvemos a ajustar a [n-k+2..n] para lo que restamos los dos últimos términos j=n-1, j=n y sumamos los dos primeros j=n-k, j=n-k+1. En la quinta línea reponemos B y finalmente en la sexta agrupamos.
Sumamos A+B+C:
| ∑j=n-k+2..n (j2+j-3) | n! | = A + B + C = |
| j! |
| = - 3 ∑j=n-k+2..n | n! | - |
| j! |
| - 1 + | n! | + ∑j=n-k+2..n | n! | - |
| (n-k+1)! | j! |
| - 2 - n | + | 2 n! | + | n! | + 2 ∑j=n-k+2..n | n! | = |
| (n-k+1)! | (n-k)! | j! |
| = -(n+3) | + | 3 n! | + | n! | = -(n+3) + | (n-k+4) n! |
| (n-k+1)! | (n-k)! | (n-k+1)! |
Se observa que los sumatorios se anulan llegando finalmente a la identidad [3] que queríamos demostrar y que equipara las dos soluciones
| ∑j=n-k+2..n (j2+j-3) | n! | = - (n+3) + | (n-k+4) n! |
| j! | (n-k+1)! |
Permutaciones, Variaciones, K-Tuplas y Convoluciones exponenciales
Este apartado servirá de recopilatorio de lo visto sobre las recurrencias de los algoritmos para generar permutaciones y variaciones, así como los que calculan el valor numérico de las K-Tuplas y las convoluciones exponenciales de factoriales y potencias. El primer algoritmo para generar las permutaciones tenía esta recurrencia:
| T(n) = { | 1 | si n≤2 |
| n T(n-1) + n2 + n + 1 + n n! | si n>2 |
La solución obtenida con la técnica de la función generadora era esta:
| T(n) = n! ( | n2+n | ) - (n+3) | + 4 ∑j=3..n | n! |
| 2 | j! |
En los apartados anteriores vimos la recurrencia para generar las variaciones:
| T(n, k) = | { | 1 | k = 1 |
| n T(n-1, k-1) + n2 + n + 1 + k n!/(n-k)! | k > 1 |
Con esta solución:
| T(n, k) = | n! | ( | k2+k | ) - (n+3) + 4 ∑j=n-k+1..n | n! |
| (n-k)! | 2 | j! |
Se observa la similitud entre ambas recurrencias, pues en la de las variaciones si k=n llegamos a la de las permutaciones, con la única salvedad que en esta el caso base es con n=2 y por eso el rango del sumatorio de la primera empieza en 3. Veamos ahora la relación que hay con las K-Tuplas y las Convoluciones exponenciales de factoriales y potencias.
La recurrencia del algoritmo para generar las K-Tuplas era así:
| K(n, k) = { | 0 | n<k |
| kk = k! | n=k | |
| n K(n-1, k) + nk | n>k |
Con esta solución:
| K(n, k) = ∑j=0..n-k | n! |
| j! |
Recuerde que V(n, k) = nk = n!/(n-k)! pues el factorial descendente nk es lo mismo que las variaciones V(n, k). Con k=0 la recurrencia se convierte en esto que vimos para introducir las recurrencias lineales con coeficientes variables:
| K(n) = { | 1 | si n=0 |
| n K(n-1) + 1 | si n>0 |
Y con esta solución:
| K(n) = ∑j=0..n | n! |
| j! |
Vemos que el término de la recurrencia n K(n-1) es el que produce en la solución el sumatorio ∑j=0..n n!/j!. Es de esto de donde salen los sumatorios de las soluciones que hemos alcanzado para las permutaciones y variaciones. Ese sumatorio también se puede expresar con la función gamma incompleta:
La convolución exponencial de factoriales y potencias tenía esta recurrencia:
| EC(n, k) = { | 0 | si n=0 |
| n EC(n-1, k) + nk | si n>0 |
Con esta solución:
| EC(n, k) = ∑j=0..n | n! jk |
| j! |
Observe como la recurrencia de las K-Tuplas K(n, k) contiene el término nk que es el factorial descendente e igual a las variaciones sin repetición V(n, k). Y la recurrencia de las convoluciones EC(n, k) contiene el término nk que es igual que las variaciones con repetición, como veremos en un siguiente tema.
Y también vimos que hay una relación con las K-Tuplas, exponiendo un resumen de convoluciones. Con k=0 teníamos que
| EC(n, 0) = K(n, 0) = ∑j=0..n | n! |
| j! |
Con k=1 teníamos que EC(n, 1) = EC(n, 0) - 1 que expresado con sumatorios es esto:
| ∑j=0..n j | n! | = - 1 + ∑j=0..n | n! |
| j! | j! |
Para k=2 teníamos
que expresado en sumatorios es esto:
| ∑j=0..n j2 | n! | = - 2 - n + 2 ∑j=0..n | n! |
| j! | j! |
Usando lo anterior vemos de donde sale el término -(n+3) + 4 ∑j=0..n n!/j! en las soluciones de las recurrencias (aunque con otro índice inicial en el rango del sumatorio):
| ∑j=0..n (j2+j+1) | n! | = EC(n, 2) + EC(n, 1) + EC(n, 0) = |
| j! |
| = -(n+3) + 4 EC(n, 0) = -(n+3) + 4 ∑j=0..n | n! |
| j! |
Podemos cambiar el rango del sumatorio en [6] con m ≤ n de esta forma:
| ∑j=n-m..n j | n! | = ∑j=n-m..n | n! | = ∑j=n-m-1..n-1 | n! | = |
| j! | (j-1)! | j! |
| = | n! | - | n! | + ∑j=n-m..n | n! |
| (n-m-1)! | n! | j! |
Así que ajustando rangos podemos asegurar que:
| ∑j=n-m..n j | n! | = - 1 + | n! | + ∑j=n-m..n | n! |
| j! | (n-m-1)! | j! |
Y también podemos cambiar el rango en [7] con m ≤ n de esta forma:
| ∑j=n-m..n j2 | n! | = ∑j=n-m..n j | n! | = ∑j=n-m-1..n-1 (j+1) | n! | = |
| j! | (j-1)! | j! |
| = ∑j=n-m-1..n-1 j | n! | + ∑j=n-m-1..n-1 | n! | = |
| j! | j! |
| = | (n-m-1) n! | - | n n! | + ∑j=n-m..n j | n! | + | n! | - | n! | + ∑j=n-m..n | n! | = |
| (n-m-1)! | n! | j! | (n-m-1)! | n! | j! |
| = | (n-m-1) n! | - n - 1 + | n! | + ∑j=n-m..n | n! | + | n! | - 1 + ∑j=n-m..n | n! |
| (n-m-1)! | (n-m-1)! | j! | (n-m-1)! | j! |
En la última línea hemos usado el resultado [8] y tras agrupar podemos asegurar que:
| ∑j=n-m..n j2 | n! | = | (n-m+1) n! | - n - 2 + 2 ∑j=n-m..n | n! |
| j! | (n-m-1)! | j! |
Usando las expresiones anteriores podemos demostrar la identidad del apartado anterior que volvemos a reproducir aquí:
| ∑j=n-k+2..n (j2+j-3) | n! | = - (n+3) + | (n-k+4) n! |
| j! | (n-k+1)! |
En la parte izquierda separamos la suma j2+j-3 viendo que m = k-2 en tres componentes. El último es
| - 3 ∑j=n-(k-2)..n | n! |
| j! |
Aplicamos [8] al componente con j
| ∑j=n-(k-2)..n j | n! | = - 1 + | n! | + ∑j=n-(k-2)..n | n! |
| j! | (n-(k-2)-1)! | j! |
Y aplicamos [9] al componente con j2
| ∑j=n-(k-2)..n j2 | n! | = | (n-(k-2)+1) n! | - n - 2 + 2 ∑j=n-(k-2)..n | n! |
| j! | (n-(k-2)-1)! | j! |
Si sumamos [10], [11] y [12] vemos que los sumatorios se anulan, quedando tras sumar las dos fracciones la identidad que queríamos demostrar
| ∑j=n-k+2..n (j2+j-3) | n! | = - (n+3) + | (n-k+4) n! |
| j! | (n-k+1)! |