Combinaciones sin repetición: algoritmo mejorado
Combinaciones sin repetición con algoritmo mejorado
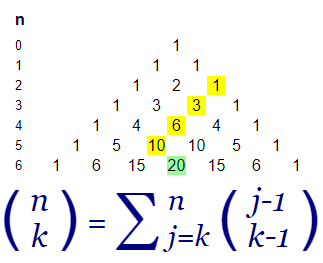
Hay varias identidades relacionadas con los coeficientes binomiales. Una de ellas es la que vemos en la Figura, obtenida a partir de la denominada identidad Hockey-stick. Vemos que C(6, 3) = C(5, 2)+C(4, 2)+C(3, 2)+C(2, 2) = 10+6+3+1 = ∑j=2..5 C(j, 2) = 20. Ese último sumatorio también lo podemos expresar como ∑j=3..6 C(j-1, 3-1) = 20, de lo que obtenemos la fórmula general C(n, k) = ∑j=k..n C(j-1, k-1). La denominación hockey stick proviene de la forma palo de hockey que se visualiza en el Triángulo de Pascal.
Se observa que es una expresión recurrente que podría servirnos para buscar una versión mejorada del problema de obtener los subconjuntos combinaciones de un conjunto que vimos en el tema anterior. Es importante entender que no buscamos el valor numérico de C(n, k), sino construir ese conjunto de combinaciones. Por ejemplo, las combinaciones sin repetición de la lista de letras {a, b, c, d} tomados en subconjuntos de dos elementos sería una lista con los subconjuntos {{a, b}, {a, c}, {a, d}, {b, c}, {b, d}, {c, d}}.
En la primera versión de este algoritmo del tema anterior habíamos usado la identidad básica del Triángulo de Pascal C(n, k) = C(n-1, k-1) + C(n-1, k), obteniendo el coste T(n, k) = 2 ( ∑j=0..k C(n, j) ) - 1 en la versión básica que no tenía en cuenta el coste de la copia. Tomemos ahora la identidad siguiente para ver si nos conduce a una mejora de ese coste:
C(n, k) = ∑j=k..n C(j-1, k-1)
Para demostrar que esta expresión es cierta desplegamos la serie:
Tomando el principio matemático C(n, k) = C(n-1, k-1) + C(n-1, k) que ya hemos usado repetidas veces antes, que podemos expresar como C(n-1, k-1) = C(n, k) - C(n-1, k), vemos que cada termino de la suma anterior empezando por el final es como cada una de las líneas siguientes:
Observe que al sumar los términos en rojo en la primera y segunda línea se anulan. Y así todos los demás quedando sólo el primero y el último. Dado que cuando n < k ⇒ C(n, k) = 0 entonces como k-1 < k ⇒ C(k-1, k) = 0 obteniendo finalmente la demostración:
Demostrando la fórmula del sumatorio con función generadora
Aunque en el apartado anterior demostramos la recurrencia vista para n≥k
C(n, k) = ∑j=k..n C(j-1, k-1)
también podríamos generalizarla para cualquier caso así:
C(0, k) = 0 si k> 0
C(n, 0) = 1
C(n, k) = ∑j=k..n C(j-1, k-1)
En este apartado vamos a obtener lo mismo usando la técnica de la función generadora. Esto nos servirá para aplicarlo al resto del tema y verlo desde otra perspectiva. Para ello partiremos de la siguiente recurrencia, donde X(n, k) es, supuestamente, una función combinatoria desconocida que al final hemos de identificar con C(n, k):
X(0, k) = 0 si k> 0
X(n, 0) = 1
X(n, k) = ∑j=k..n X(j-1, k-1)
Usaremos la siguiente función generadora:
Veamos las condiciones iniciales
| Gn,0(x, y) = ∑n≥0 X(n, 0) xn = | 1 |
| 1-x |
Como la recurrencia tiene un sumatorio, intentaremos evitarlo haciendo esto:
Entonces obtenemos X(n+1, k+1) = X(n, k) + X(n, k+1) que es lo mismo que la identidad del Triángulo de Pascal C(n, k) = C(n-1, k-1) + C(n-1, k) si incrementamos un índice C(n+1, k+1) = C(n, k) + C(n, k+1) como era de esperar. Apliquemos la función generadora a la identidad obtenida:
Expresemos X(n+1, k+1) en función de X(n, k)
| = | 1 | + 1 - 1 + ∑n,k≥0 X(n+1, k+1) xn+1 yk+1 = |
| 1-x |
| = | 1 | + xy ∑n,k≥0 X(n+1, k+1) xn yk |
| 1-x |
De donde
| ∑n,k≥0 X(n+1, k+1) xn yk = | 1 | ( G(x, y) - | 1 | ) |
| xy | 1-x |
Expresemos X(n, k+1) en función de X(n, k)
| = | 1 | + ∑n,k≥0 X(n, k+1) xn yk+1 = |
| 1-x |
| = | 1 | + y ∑n,k≥0 X(n, k+1) xn yk |
| 1-x |
De donde
| ∑n,k≥0 X(n, k+1) xn yk = | 1 | ( G(x, y) - | 1 | ) |
| y | 1-x |
Sustituyendo tenemos
| 1 | ( G(x, y) - | 1 | ) = G(x, y) + | 1 | ( G(x, y) - | 1 | ) |
| xy | 1-x | y | 1-x |
Despejando obtenemos la función generadora:
| G(x, y) = | 1 |
| 1-x-xy |
Multiplicamos y dividimos por 1-y:
| G(x, y) = | 1-y | = |
| (1-y)(1-x-xy) |
| = | 1 | - | y |
| (1-y)(1-x-xy) | (1-y)(1-x-xy) |
El primer término ya lo conocimos en el tema anterior al ver los coeficientes binomiales con 1/(1-x-xy) = ∑n≥0 (1+y)n xn que con 1/(1-y) = ∑k≥0 yk nos queda:
| 1 | = ∑n,k≥0 (1+y)n xn yk |
| (1-y)(1-x-xy) |
Para el segundo término hacemos lo mismo
| y | = ∑n,k≥0 y (1+y)n xn yk |
| (1-y)(1-x-xy) |
Obviamente conocemos el Binomio de Newton (1+y)n = ∑j≥0 C(n, j) y j con lo que tenemos:
Nuestro término general es entonces:
Como j≤k podemos ajustar los índices, teniendo en cuenta que
por lo que finalmente obtenemos:
con lo que obtenemos el resultado esperado X(n, k) = C(n, k).
Implementando algoritmo para generar combinaciones
Implementemos eso en un algoritmo:
// C(n, k) = ∑j=k..n C(j-1, k-1)
function combine2(list=[], k=0, n=list.length, res=Array.from({length:k}, ()=>""), result=[], n0=list.length, k0=res.length){
if (k===0){
result.push(copy(res));
} else {
for (let j=n; j>=k; j--){
res[k0-k] = list[n0-j];
combine2(list, k-1, j-1, res, result);
}
}
return result;
}En este algoritmo n0 y k0 son los valores en la llamada inicial combine2(n0, k0). En el bucle he invertido el rango [k, n] con objeto de que el conjunto resultado salga con el mismo orden que el algoritmo que vimos en el tema anterior, pero a efectos de la definición de la recurrencia se considera ese rango [k, n] con la llamada interna combine2(list, k-1, j-1).
Antes de estudiar el coste haremos una prueba experimental. Consideremos los costes con el algoritmo del tema anterior que denominaremos T1(n, k) y con este mejorado T2(n, k), obteniendo los valores para n=6 con 0 ≤ k ≤ 6:
n=6 k C(n,k) T1(n,k) T2(n,k) T1(n,k)-T2(n,k) --------------------------------------------- 0 1 1 1 0 1 6 13 13 0 2 15 43 41 2 3 20 83 69 14 4 15 113 69 44 5 6 125 41 84 6 1 127 13 114 T1(n, k) - T2(n, k) = T1(n, k-2) + 1 => T2(n, k) = T1(n, k) - T1(n, k-2) - 1
Se observa que en esta prueba se cumple:
Recordando el coste del algoritmo del tema anterior:
Entonces
De forma experimental hemos llegado a obtener el coste para este algoritmo mejorado. La función generadora G(x, y) con ese término general es (wolframalpha):
| = | 2xy2-2y2+1-x+xy |
| (1-x)(1-y)(1-x-xy) |
Si F(x, y) es la función generadora de T1(n, k) del tema anterior que recordamos nuevamente:
| = | 1-x+xy |
| (1-x)(1-y)(1-x-xy) |
Vemos que relación hay entre G(x, y) y F(x, y)
| G(x,y) = | 2xy2-2y2+1-x+xy | = |
| (1-x)(1-y)(1-x-xy) |
| = | 1-x+xy | - | 2y2(1-x) | = |
| (1-x)(1-y)(1-x-xy) | (1-x)(1-y)(1-x-xy) |
| = F(x, y) - | 2y2 |
| (1-y)(1-x-xy) |
Denominemos el término de la derecha como H(x, y), ecuación que tiene el siguiente desarrollo en series (wolframalpha):
| H(x, y) = | 2y2 | = ∑n,k≥0 2y2(1+y)n xnyk |
| (1-y)(1-x-xy) |
La resta F(x, y) - H(x, y) nos devuelve la serie que sustenta G(x, y) (wolframalpha):
| = | 2xy2-2y2+1-x+xy |
| (1-x)(1-y)(1-x-xy) |
Vemos que este algoritmo mejorado resta el coste H(x, y) al primer algoritmo. Pero todo esto es una suposición experimental. Intentaré en los siguientes apartados que se sustente matemáticamente.
Desarrollo para resolver el coste del algoritmo mejorado (sin coste de copia)
Este algoritmo mejorado se basa en el principio matemático siguiente que ya demostramos en el apartado anterior:
Con este principio se construye nuestro algoritmo, donde la serie equivale a un bucle for. Ya comentamos que es un bucle invertido, es decir, en lugar de ser [k, n] es [n, k]. Lo hacemos así con el único objetivo de que el resultado salga ordenado, pero realmente es indiferente para la ejecución del algoritmo. Sin embargo hay que tener cuidado cuando equiparamos un bucle de un algoritmo con una serie matemática, pues una serie con rango invertido tiene como resultado cero, el elemento neutro de la suma. Es decir, si en general j > k ⇒ ∑i=j..k ai = 0. Volveremos a incidir sobre esto porque es un aspecto clave.
Volvemos a repetir aquí el algoritmo que vamos a analizar:
function combine2(list=[], k=0, n=list.length, res=Array.from({length:k}, ()=>""), result=[], n0=list.length, k0=res.length){
if (k===0){
iter += 1;
result.push(copy(res));
} else {
iter += 1;
for (let j=n; j>=k; j--){
iter += 1;
res[k0-k] = list[n0-j];
combine2(list, k-1, j-1, res, result);
}
}
return result;
}Esta es la definición planteada, donde ahora no contemplamos el coste de copiar cada resultado parcial:
| T(n, k) = { | 1 | if k=0 |
| 1 + ∑j=k..n (1 + T(j-1, k-1)) | if k>0 |
Lo llamamos básico pues en el desarrollo a continuación descubriremos las dudas con las condiciones iniciales. En las definiciones de algoritmo del tema anterior teníamos claro las condiciones iniciales:
Pero en este segundo caso no está tan claro, pues no tienen porque ser las mismas:
Parece obvio que T(n, 0) = 1 puesto que vemos en el algoritmo que si k=0 se produce una única iteración, entrando en el condicional if (k===0) y por lo tanto T(n, 0) = 1. Obtenemos Gn,0(x, y):
| Gn,0(x, y) = ∑n≥0 T(n, 0) xn = ∑n≥0 xn = | 1 |
| 1-x |
Si queremos comprobar que T(n, 0) = 1 consideremos la solución general obtenida por experimentación T(n, k) = 2 C(n+1, k) - 1 y que luego demostraremos que es así, usándola de esta forma:
| T(n, 0) = 2 C(n+1, 0) - 1 = 2 | (n+1)! | - 1 = 2-1 = 1 |
| 0! (n+1-0)! |
Por otro lado también es obvio que T(0, 0) =1 pues es un caso particular con k=0, con lo que tenemos:
Veamos ahora T(0, k), que en el tema anterior era 1 y ahora no es exactamente eso. En el algoritmo vemos que si k>0 entra en el condicional donde está el bucle que itera en el rango [k, 0], pero es un rango inverso que supone que no se ejecute el bucle con k>0. El coste parece ser 1 para cualquier valor de k, pero en matemáticas este bucle con rango invertido si tiene sentido cuando intentamos expresar la recurrencia como una serie. Si el bucle equivale a una serie, entonces con m>n ⇒ ∑j=m..n aj = 0 resultando el elemento neutro de la suma.
Para aclarnos apliquemos la solución experimental T(n, k) = 2 C(n+1, k) - 1 a los primeros valores de k con n=0:
| T(0, 0) = 2 C(1, 0) - 1 = 2 | 1! | - 1 = 2×1 - 1 = 1 |
| 0! (1-0)! |
| T(0, 1) = 2 C(1, 1) - 1 = 2 | 1! | - 1 = 2×1 - 1 = 1 |
| 1! (1-1)! |
| T(0, 2) = 2 C(1, 2) - 1 = 2 | 1! | - 1 = 2×0 - 1 = -1 |
| 2! (1-2)! |
| T(0, 3) = 2 C(1, 3) - 1 = 2 | 1! | - 1 = 2×0 - 1 = -1 |
| 3! (1-3)! |
| T(0, k) = 2 C(1, k) - 1 = 2 | 1! | - 1 = 2×0 - 1 = -1 |
| k! (1-k)! |
En general si k≤1 ⇒ C(1, k) = 1 y si k>1 ⇒ C(1, k) = 0. Puede comprobarlo en WolframAlpha. Vease que tenemos un factorial negativo en el denominador con k>1. El factorial negativo no está definido, pero en series de potencias entendemos que el término (1-k)! → ∞ cuando k→∞, y dado que el numerador es uno entonces el cociente 1 / (k! ∞) → 0.
Entonces tenemos que si k=0 ∨ k=1 ⇒ T(0, k) = 1 y si k≥2 ⇒ T(0, k) = -1. Vease además que con T(0, k) y T(n, 0) tenemos que si n=0 ∧ k=0 en ambos casos T(0, 0) =1. Con esto las condiciones iniciales son
En un apartado más abajo incidiremos sobre estas condiciones iniciales y su implementación en el algoritmo. Veamos ahora G0,k(x, y) usando estas condiciones iniciales:
| = 1 + y - y2 | 1 | = | 1-2y2 |
| 1-y | 1-y |
Expresemos T(n, k) = 1 + ∑j=k..n 1+T(j-1, k-1) en función de n+1 y k+1 como hicimos en el primer apartado
Por lo tanto nuestra recurrencia en términos de n+1 y k+1 queda así:
Como hicimos en el primer apartado apliquemos series a esta expresión
donde hemos de obtener G(x, y) = ∑n,k≥0 T(n, k) xnyk. Empezaremos por obtener el término general para T(n, k+1):
de donde
| ∑n,k≥0 T(n, k+1) xnyk = | 1 | ( G(x, y) - | 1 | ) |
| y | 1-x |
Y ahora el término general para T(n+1, k+1):
de donde
| ∑n,k≥0 T(n+1, k+1) xnyk = | 1 | ( G(x, y) - | 1 | - | 1-2y2 | + 1 ) |
| xy | 1-x | 1-y |
Sustituimos en la expresión de series:
| 1 | ( G(x, y) - | 1 | - | 1-2y2 | + 1 ) = |
| xy | 1−x | 1-y |
| 1 | + G(x, y) + | 1 | ( G(x, y) - | 1 | ) |
| (1-x)(1-y) | y | 1-x |
De donde se deduce la función generadora de nuestro algoritmo mejorado:
| G(x, y) = | 2xy2-2y2+1-x+xy |
| (1-x)(1-y)(1-x-xy) |
Es la misma que obtuvimos de forma experimental y que puede comprobarse en wolframalpha. Teniendo la expresión G(x, y) hemos de buscar el término general. Para ello separemos en dos partes como hicimos en el apartado experimental:
Entonces el término general es la siguiente resta, usando el término general de F(x, y) que obtuvimos en el primer apartado:
El coste TH resta y, por tanto, mejora al de TF. Estas son las dos funciones generadoras:
| F(x, y) = | 1-x+xy |
| (1-x)(1-y)(1-x-xy) |
| H(x, y) = | 2y2-2xy2 | = | 2y2(1-x) | = | 2y2 |
| (1-x)(1-y)(1-x-xy) | (1-x)(1-y)(1-x-xy) | (1-y)(1-x-xy) |
Puede ver en wolframalpha la expresión en series de H(x, y), aunque en el desplegable siguiente puede ver el cálculo formal usando desarrollo de Taylor:
| H(x, y) = | 2y2 | = ∑n,k≥0 2y2(1+y)nxnyk |
| (1-y)(1-x-xy) |
Por un lado ya conocemos la siguiente identidad binomial:
Y por otro haremos esto
Como 2 ≤ j ≤ k entonces
entonces
siendo el término general el siguiente:
Usando la igualdad C(n, k) + C(n, k-1) = C(n+1, k) tenemos finalmente la solución buscada:
En esta forma se visualiza que el coste final se reduce con respecto a la solución del primer apartado en k-2+1 términos de la serie:
En cualquier caso la solución es más cómoda de usar de esta forma:
Estas soluciones hay que ajustarlas como veremos en el siguiente apartado. Veáse que en la solución se observa el principio en que se basa este algoritmo mejorado:
Ajustar algoritmo mejorado para C(n, k) con k>n+1 e incoporar coste de argumentos
En un apartado anterior descubrimos las condiciones iniciales necesarias para representar la recurrencia como series:
Hay que tener en cuenta que estas condiciones iniciales contemplan que pueda darse el caso k > n, cuando sabemos que las combinaciones C(n, k) en este caso no existen. O dicho de otra forma, existen pero supone un conjunto vacío, pues no se pueden combinar n elementos en subconjuntos de k elementos cuando k>n. Pero como necesitábamos expresar como series la posibilidad de que k>n, adaptaremos también el código del algoritmo en la implementación para contemplar esto.
Vease que con cualquier n>0 ∧ k>0 cuando n = k tenemos T(n, n+1) = 1, T(n, n+2) = -1, T(n, n+3) = -1, ... siendo -1 todos los valores a partir de k > n+1. Por ejemplo, consideremos n=3 y veamos los valores del coste calculado T(n, k) = 2 C(n+1, k) - 1 para valores de k=0, 1, 2, 3, ...
| T(n, k) = 2 C(n+1, k) - 1 |
|---|
| T(3, 0) = 2 C(4, 0) - 1 = 1 |
| T(3, 1) = 2 C(4, 1) - 1 = 7 |
| T(3, 2) = 2 C(4, 1) - 1 = 11 |
| T(3, 3) = 2 C(4, 3) - 1 = 7 |
| T(3, 4) = 2 C(4, 4) - 1 = 1 |
| T(3, 5) = 2 C(4, 5) - 1 = -1 |
| T(3, 6) = 2 C(4, 6) - 1 = -1 |
| ... |
| j>4 ⇒ T(3, j) = 2 C(4, j) - 1 = -1 |
Si vemos el algoritmo, cuando k>n+1 entra en la parte del else sumando un iter += 1 de la cabecera del bucle, aunque no entra en ese bucle y, por tanto, no produce nueva llamada recursiva, con lo que el coste final será 1.
function combine2(list=[], k=0, n=list.length, res=Array.from({length:k}, ()=>""),
result=[], n0=list.length, k0=res.length){
if (k===0){
iter += 1;
result.push(copy(res));
} else {
iter += 1;
for (let j=n; j>=k; j--){
iter += 1;
res[k0-k] = list[n0-j];
combine2(list, k-1, j-1, res, result);
}
}
return result;
}Sin embargo en el coste calculado 2 C(n+1, k) - 1 = -1, por lo que limitamos el coste total con Max(1, -1) = 1 para contemplar el caso de k>n+1:
La expresión anterior se deducía de la siguiente que también nos conduce al mismo resultado:
Estas dos expresiones son iguales, usando la primera en la aplicación.
Posteriormente a publicar este tema, detecto que a la hora de definir el coste del algoritmo no tuve en cuenta el coste de montar los argumentos de la llamada inicial que son directamente proporcionales al tamaño del problema. En este algoritmo vemos que tenemos que crear el Array res con k posiciones vacías. Para ello dotaremos de otro argumento start para, en la primera llamada, sumar k al coste total:
function combine2(list=[], k=0, n=list.length, res=Array.from({length:k}, ()=>""),
result=[], start=true, n0=list.length, k0=res.length){
if (start) {
iter += k;
start = false;
}
if (k===0){
iter += 1;
result.push(copy(res));
} else {
iter += 1;
for (let j=n; j>=k; j--){
iter += 1;
res[k0-k] = list[n0-j];
combine2(list, k-1, j-1, res, result, start);
}
}
return result;
}De este forma el coste final de combine2(list, k) es el siguiente, donde ahora no usamos la función Max() pues la incorporación de k devolverá un valor no negativo, pero lo ajustaremos para cuando n<k devuelva k+1.
n≥k ⇒ T(n, k) = 2 C(n+1, k) - 1 + k
Algoritmo mejorado con coste de copia
El coste con copia para el algoritmo anterior le afectaba el caso cuando k=0, que en lugar de valorar en 1 el coste teníamos que valorarlo en 1+k0, siendo k0 el valor de k en la llamada inicial. En el tema anterior, apartado simplificando el coste con copia, obteníamos una solución que ahora denominamos como TFc, para aclarar con c que contiene el coste de copia:
Por otro lado teníamos
Vemos que cuando k=0 tenemos TH (n, 0) = 2 ∑j=0..-2 C(n, j) = 2×0 = 0, pues en el caso general en que m>n sucede que ∑j=m..n ai = 0, el elemento neutro de la suma. Esto quiere decir que no le afecta la longitud del resultado a devolver, así que podemos determinar que THc = TH y por tanto:
De donde finalmente obtenemos la solución incluyendo el coste de copiar cada resultado parcial:
Observe que, al igual que hicimos en el apartado anterior, en las dos sumas con rangos 0..k y 0..k-2 se anulan términos quedando una expresión más sencilla. Entonces el resultado final con coste de copia e incluyendo la limitación al máximo como hicimos en el apartado anterior es:
En definitiva es el mismo coste sin copia T(n, k) =2 C(n+1, k) - 1 más el coste de copiar R = C(n, k) resultados, cada uno con una longitud de k elementos, de tal forma que se suma el coste de copia k × R.
Tal como comentamos al final del apartado anterior, al publicar este tema omití el coste de montar el argumento res que es proporcional al tamaño del problema con longitud k, por lo que la fórmula anterior queda así:
n≥k ⇒ T(n, k) = 2 C(n+1, k) - 1 + k + k C(n, k)
Comparando el coste de ambos algoritmos
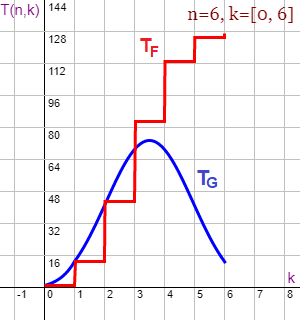
En este tema hemos encontrado las soluciones sin considerar el coste de copia ni la limitación Max(1, T(n,k)) para el caso k>n+1. Los costes del algoritmo del tema anterior y de este tema son, ambos sin considerar el coste de copia, son:
En la Figura vemos una representación gráfica del coste de TF en rojo y de TG en azul. El ejemplo presenta valores para n=6 y k tomando valores en el rango [0, 6]. Aunque las gráficas aparecen continuas, hemos de entender que son puntos sueltos en las intersecciones de los números enteros del eje k. He usado la aplicación Gráficas matemáticas usando esta entrada de texto con la definición de la gráfica.
Hasta la primera mitad de k la gráfica roja se comporta casi igual que la azul (tomando los enteros [0, 6] del eje k). A partir de ahí la azul aprovecha la ventaja de que las combinaciones hasta la mitad de n son las mismas en orden inverso que las del resto, como ya vimos en un apartado anterior con estos datos de ejemplo y que volvemos a replicar aquí. Se observa esa simetría en C(n, k) que se reproduce en TG.
n=6 k C(n,k) TF(n,k) TG(n,k) --------------------------------------------- 0 1 1 1 1 6 13 13 2 15 43 41 3 20 83 69 4 15 113 69 5 6 125 41 6 1 127 13
En resumen podríamos decir que si k<n/2 cualquiera de los dos algoritmos son igual de eficientes. En otro caso el mejorado TG se comporta mejor. Y más cuando k es o está muy cerca de n.
La cuestión que ahora se plantea es saber en que orden están estas funciones. Recordemos que una función f(n) está o se incluye en el orden de otra g(n) si se cumple lo siguiente:
| limn→∞ | f(n) | ∈ ℝ+ ⇒ f(n) ∈ O(g(n)) ∧ g(n) ∈ O(f(n)) |
| g(n) |
Supongamos que buscamos el orden en función de n de TG, manteniendo k>0 constante. Vease que
| C(n+1, k) = | (n+1)! | = | (n+1)n(n-1)...(n+1-k+1) (n+1-k)! | = |
| k! (n+1-k)! | k! (n+1-k)! |
| = | (n+1)n(n-1)...(n+1-k+1) | = | Pk(n) | ≃ | nk |
| k! | k! | k! |
Pk(n) significa un polinomio de orden (n+1) - (n+1-k+1) + 1= k, donde el término de mayor potencia es nk, entonces asintóticamente equivale a nk/k!. Para TG tenemos que:
| limn→∞ | 2 C(n+1, k) - 1 | = |
| nk / k! |
| = limn→∞ | 2 (nk / k!) | - limn→∞ | k! | = 2-0 = 2 ∈ ℝ+ |
| nk / k! | nk |
El límite del término de la derecha k!/nk es cero, pues
Y claramente si n≥k entonces nk > k!.
Entonces TG (n, k) ∈ O(nk/k!) y nk/k! ∈ O(TG (n, k)) con lo que TG ∈ O(nk/k!).
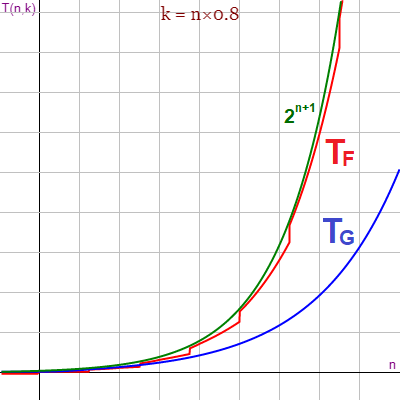
En cuanto a TF (n, k) = 2 ( ∑j=0..k C(n, j) ) - 1 vemos que el peor de los casos es cuando k=n. En este caso tenemos que 2 ( ∑j=0..n C(n, j) ) - 1 = 2n+1 -1. Por lo tanto TF ∈ O(2n+1).
En la gráfica de la Figura se observa la representación de TF (n, k) y TG (n, k) en función de n y tomando k = n×0.8 para cada valor de n, observándose el mejor comportamiento del algoritmo mejorado. Observe como TF está muy cerca, pero por debajo, de 2n+1.
Puede verla en Gráficas matemáticas usando esta definición. Se puede probar con k = n×0.5 observándose que ambas gráficas siguen la misma tendencia, en cuyo caso estarán en el mismo orden. En cualquier caso 2n+1 es un cota superior de ambas.