Combinaciones sin repetición
Combinaciones sin repetición
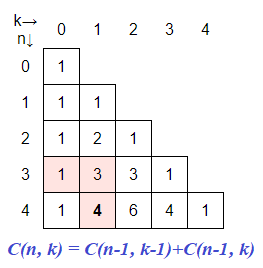
El número de combinaciones sin repetición de n elementos distintos en subconjuntos de k elementos son las posibles muestras de k elementos distintos y sin orden que pueden extraerse de los n elementos. En estas páginas las denotaremos como C(n, k) aunque las veremos como (nk). Su valor numérico se calcula con esta fórmula:
| C(n, k) = | n! |
| k! (n-k)! |
La primera aproximación para implementar un algoritmo es usar la conocida fórmula matemática con la recurrencia C(n, k) = C(n-1, k-1) + C(n-1, k) que sirve para construir el Triángulo de Pascal. La fila n son los coeficientes binomiales del polinomio (1+x)n.
En la Figura vemos un ejemplo, donde se observa en las celdas resaltadas que se cumple la recurrencia, pues C(4, 1) = C(3, 0) + C(3, 1). El triángulo se va construyendo empezando en la primera celda superior y al ir bajando vamos tomando los valores de la fila anterior. Con los valores de esa cuarta fila desarrollamos (1+x)4 = C(4,0) + C(4,1) x + C(4,2) x2 + C(4,3) x3 + C(4,4) x4 = 1 + 4 x + 6 x2 + 4 x3 + x4.
Lo que nos interesa es extraer los subconjuntos de C(n, k) más que calcular el valor númerico, valor que podemos calcular con C(n,k) = n! / (k! (n-k)!). Por ejemplo, las combinaciones sin repetición de la lista de letras {a, b, c, d} tomados en subconjuntos de dos elementos sería una lista con los subconjuntos {{a, b}, {a, c}, {a, d}, {b, c}, {b, d}, {c, d}}. Implementamos el siguiente algoritmo con la recurrencia:
C(0, k) = 0,
C(n, k) = C(n-1, k-1) + C(n-1, k)
donde la variable global iter nos contará las iteraciones:
// C(n, k) = C(n-1, k-1) + C(n-1, k)
function combine1(list=[], k=0, n=list.length, res=[], result=[], n0=list.length){
if (k===0){
iter += 1;
result.push(copy(res));
} else if (n===0) {
iter += 1;
} else {
iter += 1;
res.push(list[n0-n]);
combine1(list, k-1, n-1, res, result);
res.pop();
combine1(list, k, n-1, res, result);
}
return result;
}Es un algoritmo recursivo del tipo final, pues hacemos una inmersión de parámetros pasando los resultados parciales res y el resultado final result en los argumentos de las sucesivas llamadas. La primera llamada la hacemos con combine1(list, k), pues se obtiene n de la longitud de la lista con n = list.length. La denominamos combine1 pues es una primera versión dado que en otro apartado veremos una segunda versión combine2 más eficiente.
La esencia del algoritmo es usar el resultado parcial res e ir poniendo con push() elementos de la lista hasta que contenga k elementos (k=0), cuando incorporamos el resultado parcial en la lista de resultado final. Y luego vamos quitando el último elemento con pop() y poniendo otro que aún no han sido seleccionado. En la aplicación Combine Tools se ofrece una traza de la evolución en la ejecución.
Estudiemos el coste de este algoritmo usando lo que vimos en el tema Coste de los recursivos. En el código anterior tenemos unas líneas iter += 1; que se ejecutan solo con el fin de computar el coste calculado. Este coste es, entonces, la suma de las iteraciones por las que pasa el recursivo, valor que debe ser igual que el que obtengamos con la resolución de la recurrencia de este algoritmo.
Si se quiere un código final sin estas necesidades, podemos también eliminar la línea else if (n===0) y poner el siguiente como else if (n>0), puesto que cuando n=0 realmente no se hace nada más que devolver el resultado, aunque computa como iteración. Este sería el código simplificado:
function combine1(list=[], k=0, n=list.length, res=[], result=[], n0=list.length){
if (k===0){
result.push(copy(res));
} else if (n>0) {
res.push(list[n0-n]);
combine1(list, k-1, n-1, res, result);
res.pop();
combine1(list, k, n-1, res, result);
}
return result;
}En la aplicación Combine Tools tenemos la posibilidad de computar el coste de la copia o no hacerlo. Se trata de la sentencia result.push(copy(res)) que copia el resultado parcial (uno de los subconjuntos conseguidos de longitud k0 inicial) en el resultado final. Hemos de hacerlo así puesto que las variables en JavaScript se pasan por referencia y cuando tengamos un subconjunto hemos de preservar sus valores en ese momento. Para estudiar el coste más fácilmente suponemos que el coste de esta copia es 1. En otro apartado contemplaremos este coste, situación más realista, pues copiar una lista de longitud k tiene un coste k dado que hay que recorrer la lista.
Coste de combinar sin repetición (sin coste de copia)
En la primera llamada combine1(list, k) obtenemos n de la longitud. En principio si no se cumpliera 0 ≤ k ≤ n debería acusar un error, pues parece que no tiene sentido hablar de C(n, k) cuando k > n. Matemáticamente si puede estar definido dando como valor cero. Es decir, que combinar una lista de elementos en subconjuntos mayores que la longitud de la lista da por resultado una lista vacía. En otro apartado incideremos más sobre esto.
Si n=0 entonces k=0, por lo que el algoritmo detecta en la primera llamada k===0, cuyo coste es 1. En el avance del algoritmo cuando k>0 ∧ n=0 el algoritmo no hace nada, pero finaliza y devuelve el resultado, cuyo coste también es 1. En otro caso si n>0 entramos en la parte de llamadas recursivas. Tenemos dos llamadas y dos sentencias push() y pop(), que individualmente tienen coste 1 y cuando hay más de una se computa la de mayor coste, por tanto es 1. Este sería el desglose del coste:
| T(n, k) = { | 1 | si k=0 ∨ n=0 |
| T(n-1, k-1) + T(n-1, k) + 1 | si n ≥ k |
Esta es una recurrencia con dos variables. Los métodos para analizar el coste de un recursivo de una variable no nos sirven para esto, debiendo usar la técnica de función generadora que ya vimos en el tema anterior para una variable. Conviene leer primero ese tema para entender como se aplican las funciones generadoras para resolver las recurrencias. Evitamos los índices como n-1 y k-1 poniendo la recurrencia así:
Definimos una función generadora:
Antes de multiplicar la recurrencia por xn yk veamos algunas cosas que necesitaremos. Las condiciones iniciales son las siguientes, donde se identifican series geométricas:
| Gn,0 (x, y) = ∑n≥0 T(n, 0) xn y0 = ∑n≥0 xn = | 1 |
| 1-x |
| G0,k (x, y) = ∑k≥0 T(0, k) x0 yk = ∑k≥0 yk = | 1 |
| 1-y |
Veamos como podemos obtener el termino (n+1, k+1):
Resultando que:
| = | 1 | ( ∑n,k≥0 T(n, k) xn yk - ∑n≥0 T(n, 0) xn - ∑k≥0 T(0, k) yk + T(0, 0) ) = |
| xy |
| = | 1 | ( G(x, y) - Gn,0(x, y) - G0,k(x, y) + T(0, 0) ) = |
| xy |
| = | 1 | ( G(x, y) - | 1 | - | 1 | + 1 ) |
| xy | 1-x | 1-y |
Veamos como podemos obtener el termino (n, k+1):
Resultando que:
| = | 1 | (∑n,k≥0 T(n, k) xn yk - ∑n≥0 T(n, 0) xn) = |
| y |
| = | 1 | (G(x, y) - Gn,0(x, y)) = |
| y |
| = | 1 | (G(x, y) - | 1 | ) |
| y | 1-x |
Por último la serie geométrica con 2 variables queda así:
| ∑n,k≥0 xn yk = | 1 | |
| (1-x)(1-y) |
Multiplicamos la recurrencia por xn yk:
Aplicamos sumas a todos los términos
Identificando con [1], [2], [3] y [4]
| 1 | (G(x,y)- | 1 | - | 1 | +1) = |
| xy | 1-x | 1-y |
| = G(x, y)+ | 1 | (G(x, y) - | 1 | )+ | 1 | |
| y | 1-x | (1-x)(1-y) |
Despejando G(x, y) obtenemos esto:
| G(x, y) = | 1-x+xy |
| (1-x)(1-y)(1-x-xy) |
Lo primero que tenemos que hacer en este punto es simplificar en fracciones para obtener términos más simples a la hora de identificar su representación en serie. Después de varios intentos vemos que una parte de la expresión nos conduce a una simplificación:
| 1-x+xy | = | A | + | B | ⇒ A=-1 ∧ B=2 |
| (1-x)(1-x-xy) | 1-x | 1-x-xy |
Por lo tanto:
| G(x, y) = | 1-x+xy | = | 2 | - | 1 |
| (1-x)(1-y)(1-x-xy) | (1-y)(1-x-xy) | (1-x)(1-y) |
El término de la derecha es claramente la serie geométrica en dos variables:
| 1 | = ∑n≥0 xn ∑k≥0 yk= ∑n,k≥0 xn yk |
| (1-x)(1-y) |
Algo hemos aliviado. Ahora solo falta lidiar con el término de la izquierda, cuya serie se obtiene y explica con más detalle en el apartado siguiente (y que también puede comprobar en Wolframalpha sin particularizar el rango 0..k):
| 2 | = ∑n,k≥0 2 ( ∑j=0..k C(n, j) y j ) xn yk |
| (1-y)(1-x-xy) |
Con lo que obtenemos:
| G(x, y) = | 2 | - | 1 | = |
| (1-y)(1-x-xy) | (1-x)(1-y) |
Esta expresión también podemos ponerla en función de (1+y)n de un forma más compacta (explicado en el apartado siguiente):
Por lo tanto el término general en [1] que era G(x, y) = ∑n,k≥0 T(n, k) xn yk es el coeficiente ubicando en la posición n, k de las variables x, y tomado de [8] que es el siguiente:
Este coste sin copia coincide con el contador de iteraciones, lo que puede comprobarse en la aplicación. En el código para calcular este coste usamos lo siguiente, donde la opción withCopyCost la veremos en el apartado siguiente:
let calcCost = 0;
for (let j=0; j<=k; j++){
calcCost += factorial(n) / (factorial(j)*factorial(n-j));
}
if (withCopyCost) {
...
} else {
calcCost = 2 * calcCost - 1;
}Vemos que C(n, j) = n! / ( j! (n-j)! ) usándose la función factorial(n) implementada así:
function factorial(n){
if (n===0){
return 1;
} else {
return n*factorial(n-1);
}
}Desarrollos en dos variables: Coeficientes Binomiales
Este apartado intenta explicar que teníamos que buscar la representación en serie de la expresión [7] del apartado anterior. Primero la separamos en dos partes para simplificar la búsqueda de las series implicadas:
| 2 | = | 2 | × | 1 |
| (1-y)(1-x-xy) | 1-y | 1-x-xy |
Sabemos que la expresión de la izquierda del producto anterior es la serie geométrica multiplicada por 2:
| 2 | = 2 ∑k≥0 yk = 2 (1+y+y2+...) |
| 1-y |
Supongamos que podemos separar el término 2/(1-y) y buscar la serie de 1/(1-x-xy). Si ésta tiene un término general como an,k xn, entonces el resultado es el producto de estas dos series:
| 2 | = | 2 | × | 1 | = 2 ∑k≥0 yk ∑n≥0 an,k xn = 2 ∑n,k≥0 an,k xn yk |
| (1-y)(1-x-xy) | 1-y | 1-x-xy |
Busquemos ese término general para 1/(1-x-xy) usando el desarrollo de Taylor en x=0 considerando y constante:
| f(x, y) = | 1 | = ∑n≥0 | fx n(0, y) | xn |
| 1-x-xy | n! |
donde fx n es la derivada parcial n-ésima respecto a x. Obtengamos derivadas parciales hasta orden 3 para ver si deducimos el término general
| fx 1(x, y) = | 1+y |
| (1-x-xy)2 |
| fx 2(x, y) = | 2(1+y)2 |
| (1-x-xy)3 |
| fx 3(x, y) = | 6(1+y)3 |
| (1-x-xy)4 |
Particularizando para (0, y) nos quedan las expresiones resaltadas pues el resto se anulan, con lo que dividiendo por el factorial queda:
| fx 0(0, y) | = 1 |
| 0! |
| fx 1(0, y) | = 1+y |
| 1! |
| fx 2(0, y) | = (1+y)2 |
| 2! |
| fx 3(0, y) | = (1+y)3 |
| 3! |
El término general es fácilmente deducible, por lo que podemos suponer:
| fx n(0, y) | = (1+y)n |
| n! |
Así que obtenemos lo mismo que en la página de WolframAlpha
| f(x, y) = | 1 | = ∑n≥0 (1+y)n xn |
| 1-x-xy |
Observe que podíamos haber evitado todo lo anterior y obtener una serie geométrica como esa haciendo el cambio 1+y = a:
| 1 | = | 1 | = | 1 | = ∑n≥0 (ax)n = ∑n≥0 (1+y)n xn |
| 1-x-xy | 1-(1+y)x | 1-ax |
Si sabemos que (1+y)n = ∑j≥0 C(n, j) y j tal como se observa en la página Wikipedia: Binomial coefficient
En el enlace que pusimos de Wikipedia la expresión está en función de x y no de y, es decir, está como (1+x)n y no como (1+y)n, pero se trata de la misma expresión. En el apartado siguiente explicaremos más sobre esto. Como C(n, j) = 0 si j > n entonces el sumatorio de las combinaciones equivale al rango 0 ≤ j ≤ n:
| 1 | = ∑n≥0 (1+y)n xn = ∑n≥0 ∑j=0..n C(n, j) y j xn |
| 1-x-xy |
Podemos comprobar en WolframAlpha este resultado. Observe que en la página de Wikipedia que dijimos antes aparece esta expresión en función de 1-y-xy (donde cambiamos k por j para no confundir con la k de nuestro problema):
| 1 | = ∑n≥0 ∑j=0..n C(n, j) x j yn |
| 1-y-xy |
Es la misma expresión con el intercambio entre las variables x, y. En WolframAlpha se puede comprobar que se obtiene en función de 1-y-xy. En el siguiente apartado veremos más sobre esto.
Vea que el rango j=0..n del sumatorio se particulariza en el problema de la recurrencia del algoritmo a j=0..k, puesto que n, k son los valores iniciales de la llamada al algoritmo combine(n, k). Con esto finalmente la solución en el problema inicial es la siguiente:
| 2 | = | 2 | × | 1 | = |
| (1-y)(1-x-xy) | 1-y | 1-x-xy |
Este resultado es el calculado para la expresión [7] del apartado anterior.
Desarrollo considerando x constante
¿Y que pasa si consideramos x constante? Vamos a hacerlo:
| f(x, y) = | 1 |
| 1-x-xy |
| fy 1(x, y) = | x |
| (1-x-xy)2 |
| fy 2(x, y) = | 2 x2 |
| (1-x-xy)3 |
| fy 3(x, y) = | 6 x3 |
| (1-x-xy)4 |
Estas derivadas para y=0 resultan:
| fy 0(x, 0) | = | 1 |
| 0! | 1-x |
| fy 1(x, 0) | = | x |
| 1! | (1-x)2 |
| fy 2(x, 0) | = | 2 x2 |
| 2! | (1-x)3 |
| fy 3(x, 0) | = | 6 x3 |
| 3! | (1-x)3 |
El término general se deduce fácilmente:
| fy k(x, 0) | = | xk |
| k! | (1-x)k+1 |
Obteniendo un término general en función de k.
| 1 | = ∑k≥0 | xk | yk |
| 1-x-xy | (1-x)k+1 |
Esto significa que f(x, y) tiene estas dos representaciones en series. De hecho en el enlace de WolframAlpha que vimos antes observamos que se obtienen cuatro representaciones en series y las dos primeras son estas que hemos obtenido aquí. Observe que en esa web los sumatorios usan n en los dos casos, pero sólo son nombres de variables, pues lo que identifica las variables α, β son los índices de los sumatorios relacionados con los términos xα e yβ respectivamente e independiente de los nombres de α, β.
Es posible llegar al mismo resultado sin utilizar el desarrollo de Taylor haciendo esto:
| 1 | = | 1 | · | 1 | ||
| 1-x-xy | 1-x | 1- | x | y | ||
| 1-x | ||||||
Si ahora hacemos que a = x / (1-x) tenemos en la parte derecha la serie geométrica que ya hemos visto otras veces 1 / (1-ay) cuya serie es ∑k≥0 ak yk por lo que finalmente obtenemos:
| 1 | = | 1 | ∑k≥0 | xk | yk = ∑k≥0 | xk | yk |
| 1-x-xy | 1-x | (1-x)k | (1-x)k+1 |
Con estos cálculos alternativos vemos que no siempre es necesario usar el desarrollo de Taylor para encontrar la serie.
La representación en función de las combinaciones de la otra serie es simétrica con ésta. Por un lado tenemos esto que también vemos en el enlace anterior Wikipedia: Binomial coefficient (con la misma salvedad que vimos antes, donde en Wikipedia están en función y y aquí aparece en función de x cuyo motivo explicaremos en el apartado siguiente):
| xk | = ∑j≥0 C(j, k) x j |
| (1-x)k+1 |
Función de generación de los coeficientes binomiales
El resumen del apartado anterior es que los coeficientes binomiales de C(n, k) tienen por función generadora precisamente alguna de las dos que vimos, siendo la más usual la primera de ellas:
| 1 | = ∑n≥0 (1+y)n xn = ∑n≥0 ∑j=0..n C(n, j) y j xn |
| 1-x-xy |
Sin embargo en la página de Wikipedia: Binomial coefficient y otros documentos veo que ponen como función generadora esta:
| 1 | = ∑n≥0 (1+x)n yn = ∑n≥0 ∑j=0..n C(n, j) x j yn |
| 1-y-xy |
La diferencia está en hacer el cambio x → y. Después de todo el término general de la serie es el mismo y es independiente de las variables x, y. Pero ¿por qué obtuvimos nosotros el denominador 1-x-xy en lugar de 1-y-xy? La respuesta está en la definición de la función generadora que usemos. Nosotros partimos de [1]:
llegando a esta expresión en [5]
| 1 | (G(x,y)- | 1 | - | 1 | +1) = |
| xy | 1-x | 1-y |
| = G(x, y)+ | 1 | (G(x, y) - | 1 | )+ | 1 | |
| y | 1-x | (1-x)(1-y) |
y despejando G(x, y) en [6] y descomponiendo en fracciones obtuvimos esto:
| G(x, y) = | 1-x+xy | = | 2 | - | 1 |
| (1-x)(1-y)(1-x-xy) | (1-y)(1-x-xy) | (1-x)(1-y) |
Si en la definición de la función generadora hubiésemos intercambiado x, y:
Los siguientes cálculos serían iguales solo que habría que intercambiar esas variables. En la expresión [5] la modificación afecta a los términos resaltados con fondo amarillo, pues los demás contienen ambas variables y el intercambio los deja iguales. Si en esa expresión hacemos ese cambio y resolvemos obtendremos:
| G(x, y) = | 1-x+xy | = | 2 | - | 1 |
| (1-x)(1-y)(1-y-xy) | (1-x)(1-y-xy) | (1-x)(1-y) |
Observe que ambas son iguales a excepción del cambio de variable x, y, lo que a efectos de obtener una solución del término general es indiferente, pues al fin y al cabo no son sino nombres de variables, que bien podrían ser u, v o cualquier otra cosa. En el desarrollo de Taylor del apartado anterior aplicaríamos ahora las derivadas con respecto a y para del desarrollo de Taylor en y=0 del término 1/(1-y-xy), obteniéndose entonces como primera solución en función de (1+x)n en lugar de (1+y)n como obtuvimos.
Obviamente nuestra función generadora G(x, y) contiene más cosas que 1/(1-x-xy) o, con la otra definición 1/(1-y-xy). Y esto es debido a que nuestra recurrencia para el algoritmo era así tras aplicar el ajuste para evitar índices negativos:
Y la recurrencia para resolver C(n, k) = C(n-1, k-1) + C(n-1, k), que ajustando índices para evitar negativos es C(n+1, k+1) = C(n, k) + C(n, k+1) se define así:
Observe las diferencias: el uno final que ahora no suma. Además que T(0, k) = 1 que difiere de C(0, k) = 0 con k>0 y C(0, 0) = 1. Esto es lo que produce una G(x, y) más simple que la obtenida. Si en la expresión [5] que vimos antes intercambiamos x, y (apareciendo en color rojo donde afecta el cambio)
| 1 | (G(x,y)- | 1 | - | 1 | +1) = |
| xy | 1-x | 1-y |
| = G(x, y) + |
| + | 1 | (G(x, y) - | 1 | )+ |
| x | 1-y |
| + | 1 |
| (1-x)(1-y) |
Por otro lado vemos una correspondencia entre esos términos y la recurrencia que identificamos con los colores de fondo:
así como con la recurrencia de las combinaciones:
Por lo tanto hemos de eliminar el término con fondo verde que corresponde a la suma del uno en la primera recurrencia. Y además el término 1/(1-x) de la primera expresión con color de fondo beige toma el valor uno, pues C(0, k) = 0 si k>0 y C(0, 0) = 1, cuando antes teníamos T(0, k) = 1 para todo k. Al final tendríamos esto:
| 1 | (G(x,y)-1 | - | 1 | +1) = G(x, y)+ | 1 | (G(x, y) - | 1 | ) |
| xy | 1-y | x | 1-y |
Cuya solución es:
| G(x, y) = | 1 |
| 1-y-xy |
que es la función generadora de los coeficientes binomiales que solemos ver en la documentación.
Combinaciones con k > n
Como comentamos en el primer apartado, la aplicación admite k > n dando por resultado C(n, k) = 0. Pero el coste en este caso no es cero. Si recordamos el algoritmo:
function combine1(list=[], k=0, n=list.length, res=[], result=[], n0=list.length){
if (k===0){
iter += 1;
result.push(copy(res));
} else if (n===0) {
iter += 1;
} else {
iter += 1;
res.push(list[n0-n]);
combine1(list, k-1, n-1, res, result);
res.pop();
combine1(list, k, n-1, res, result);
}
return result;
Vemos que cuando k > n la ejecución nunca alcanzará k===0 pues sale antes por n===0. Activando la traza en la aplicación para el ejemplo C(2, 3) obtenemos esta tabla:
| iter | part | n | k | res | result |
|---|---|---|---|---|---|
| 1 | call_1 | 1 | 2 | a | |
| 2 | call_1 | 0 | 1 | a,b | |
| 3 | n=0 | 0 | 1 | a,b | |
| 3 | call_2 | 0 | 2 | a | |
| 4 | n=0 | 0 | 2 | a | |
| 4 | call_2 | 1 | 3 | ||
| 5 | call_1 | 0 | 2 | b | |
| 6 | n=0 | 0 | 2 | b | |
| 6 | call_2 | 0 | 3 | ||
| 7 | n=0 | 0 | 3 |
Se observa que se realizan 7 iteraciones, pero al no alcanzar k=0 el resultado en la variable result está vacío. El coste calculado con la solución que obtuvimos:
es para este ejemplo:
obteniendo el mismo coste 7 que el que se obtiene con el contador de iteraciones. Podemos ver que cuando k >n
En una situación de uso del algoritmo impondríamos que n≥k, pero en la aplicación lo permitiremos, pues más adelante volveremos a esto.
Coste de combinar sin repetición (con coste de copia)
Ya vimos que, para ser realistas, hemos de considerar el coste de copiar los resultados en la sentencia result.push(copy(res)). Si res tiene una longitud k debemos considerar este coste, pues copiar una lista tiene el coste de recorrerla. En el contador de iteraciones del algoritmo agregamos la longitud del resultado parcial, que viene a ser el valor de k de la llamada inicial combine1(n, k):
// C(n, k) = C(n-1, k-1) + C(n-1, k)
function combine1(list=[], k=0, n=list.length, res=[], result=[], n0=list.length){
if (k===0){
iter += 1;
if (withCopyCost) iter += res.length;
result.push(copy(res));
} else if (n===0) {
iter += 1;
} else {
iter += 1;
res.push(list[n0-n]);
combine1(list, k-1, n-1, res, result);
res.pop();
combine1(list, k, n-1, res, result);
}
return result;
}Vea que la función copy(res) equivale a un bucle como el siguiente, con un coste igual a la longitud del array. El coste de inicializar el bucle iter += 1 estaría en serie con el contador iter += 1 previo en el algoritmo, por lo que se toma el máximo de los dos que es 1, así que se prescinde ese contador del bucle que aparece como comentario.
function copy(arr=[]) {
let arrCopy = [];
// iter += 1 (ver texto)
for (let i=0; i<arr.length; i++){
iter += 1;
arrCopy[i] = arr[i];
}
return arrCopy;
}Con esto la definición de la recurrencia del coste del algoritmo es el siguiente:
| T(n, k) = | { | 1+k0 | if k=0 |
| 1 | if n=0 | ||
| T(n-1, k-1) + T(n-1, k) + 1 | if k>0 ∧ n ≥ k |
Denotamos con k0 el valor de k en la primera llamada combine1(list, k), valor k que va decreciendo en las llamadas recursivas. Ajustando índices n-1 y k-1 nos queda esto:
Para aliviar el cálculo haremos a = 1+k0
Las condiciones iniciales son ahora:
| Gn,0 (x, y) = ∑n≥0 T(n, 0) xn = ∑n≥0 a xn = | a |
| 1-x |
| G0,k (x, y) = ∑k≥0 T(0, k) yk = ∑k≥0 yk = | 1 |
| 1-y |
El desarrollo es el mismo que el del apartado anterior, tomando la función generadora G(x, y) = ∑n,k≥0 T(n, k) xn yk, multiplicando la recurrencia por xnyk, llegamos a:
| 1 | ( G(x, y) - | 1 | - | 1 | + 1 ) = |
| xy | 1-x | 1-y |
| G(x, y) + | 1 | ( G(x, y) - | 1 | ) + | 1 |
| y | 1-x | (1-x)(1-y) |
Donde ponía 1/(1-x) que procedía de Gn,0(x, y) ahora debemos poner a/(1-x):
| 1 | ( G(x, y) - | a | - | 1 | + 1 ) = |
| xy | 1-x | 1-y |
| G(x, y) + | 1 | ( G(x, y) - | a | ) + | 1 |
| y | 1-x | (1-x)(1-y) |
Despejando G(x, y) nos queda:
| G(x, y) = | axy-ax-ay+a+y |
| (1-x)(1-y)(1-x-xy) |
Separando 1/(1-y) = ∑k≥0 yk y desarrollando el resto como hicimos en el apartado anterior llegamos a esto (ver en wolframalpha):
| axy-ax-ay+a+y | = ∑n≥0 ( 2a (1+y)n - 1 - (a-1) (1+y)n+1 ) xn |
| (1-x)(1-x-xy) |
Finalmente tenemos que G(x, y) es:
Como a = 1+k0 = 1+k con el valor inicial de k0 = k cuando llamamos inicialmente al algoritmo con combine1(list, k), llegamos a la siguiente solución final:
Simplificando el coste con copia
Podemos simplificar el coste con copia del apartado anterior de esta forma:
La parte de la izquierda 2 ∑j=0..k C(n, j) - 1 es el coste sin copia que ya habíamos calculado. La parte de la derecha suma el coste de copiar los resultados parciales. Si el coste sin copia es Ts y la parte de copiar los resultados parciales es Tc = k × R, donde k es la longitud de un resultado y R es el número total de resultados, entonces el coste total será:
Es imprescindible que R = C(n, k) pues el número total de resultados tiene que ser el total de combinaciones que estamos obteniendo. Veamos si podemos llegar a ello reduciendo esto:
Partiendo de la identidad del Triángulo de Pascal que ya conocemos podemos hacer lo siguiente
Entonces en nuestra expresión [10] podemos sustituir:
Puede comprobar este resultado en Wolpframalpha, lo cual no es díficil de probar si desplegamos la suma:
Se observa que todos los términos se anulan a excepción de los señalados en rojo. Como C(n, -1) = 0 por definición, entonces llegamos al resultado buscado.
Obviamente hemos obtenido lo deseado R = C(n, k), por lo que la expresión final del coste con copia es:
Observamos que no hubiese hecho falta todo el desarrollo para obtener la parte del coste de la copia, puesto que siempre será una expresión k × R, dado que hay que copiar R resultados parciales cada uno con una longitud de k elementos.
El cálculo del coste lo implementamos con este código, en la parte donde entra con withCopyCost verdadero:
let calcCost = 0;
for (let j=0; j<=k; j++){
calcCost += binomial(n, j);
}
calcCost = 2 * calcCost - 1;
if (withCopyCost) calcCost += k * binomial(n, k);donde
function binomial(n, k) {
if (n<k) {
return 0;
} else {
return factorial(n) / (factorial(k)*factorial(n-k));
}
}