Particiones con bloques parciales y semi bloques
Parcial Bell o particiones con bloques parciales y Semi Bell o particiones con semi bloques
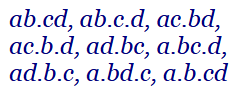
Las particiones con bloques parciales (o Bell parcial), que denominaremos pB(n, k), son las particiones de un conjunto con n elementos tal que alguno de los subconjuntos (o bloques) son de longitud igual a k. En la Figura vemos las particiones con bloques parciales de tamaño k=2 para un conjunto con n=4 elementos, donde cada partición contiene al menos un subconjunto o bloque de tamaño k=2.
Por otro lado las particiones con semi bloques parciales (o semi Bell), que denominaremos sB(n, k), son las particiones de un conjunto con n elementos tal que ninguno de los subconjuntos (o bloques) son de longitud igual a k. Por ejemplo, para el conjunto con n elementos {a, b, c} tenemos con k=1 la única partición abc expresada de forma compacta, donde ningún subconjunto o bloque tienen longitud unitaria; con k=2 tenemos abc, a.b.c; con k=3 tenemos ab.c, ac.b, a.bc, a.b.c; mientras que con k=0 o k>3 tenemos todas las particiones posibles abc, ab.c, ac.b, a.bc, a.b.c.
No debemos confundir estas particiones con bloques parciales o semi bloques con las Particiones parciales que vimos en el tema anterior, que es una aplicación directa de la recurrencia de los números de Stirling de segunda clase S2(n, k) = S2(n-1, k-1) + k × S2(n-1, k). Para las particiones parciales usamos algoritmos como kPartition(list, k), mientras que para las de bloques parciales de este tema usaremos partialPartition(list, k) y para los semi bloques semiPartition(list, k).
Por ejemplo, para el conjunto list = {a, b, c} tenemos los siguientes resultados de forma compacta:
| k | kPartition(list, k) | partialPartition(list, k) | semiPartition(list, k) |
|---|---|---|---|
| Particiones parciales con k bloques | Particiones con bloques parciales de longitud k | Particiones con semi bloques, ninguno de longitud k | |
| 0 | ∅ | abc, ab.c, ac.b, a.bc, a.b.c | abc, ab.c, ac.b, a.bc, a.b.c |
| 1 | abc | ab.c, ac.b, a.bc, a.b.c | abc |
| 2 | ab.c, ac.b, a.bc | ab.c, ac.b, a.bc | abc, a.b.c |
| 3 | a.b.c | abc | ab.c, ac.b, a.bc, a.b.c |
Se observa que para kPartition(list, k) el valor de k indica el número de subconjuntos que hay en cada subresultado o partición. Recuerde que los subconjuntos (o bloques) en la forma compacta se separan con un punto. Mientras que partialPartition(list, k) filtra las particiones que contengan al menos un bloque de longitud k. Por otro lado semiPartition(list, k) filtra las particiones que no contengan algún bloque de longitud k.
Con k=0 obtenemos las particiones totales que veíamos en temas anteriores con algoritmos que denominábamos como partition(list), con lo que en este caso partialPartition(list, 0) = semiPartition(list, 0) = partition(list)
Por otro lado observamos que partition(list) = ⋃k=1..n kPartition(list, k) siendo n la longitud del conjunto de partida.
Analizando el conjunto {a, b, c} con n=3 tenemos estas B(n) = B(3) = 5 particiones de forma compacta que vemos en la siguiente tabla en la primera columna con k=0:
| k=0 | k=1 | k=2 | k=3 |
|---|---|---|---|
| abc | abc | ||
| ab.c | ab.c | ab.c | |
| ac.b | ac.b | ac.b | |
| a.bc | a.bc | a.bc | |
| a.b.c | a.b.c | ||
| 5 | 4 | 3 | 1 |
En la segunda columna vemos las 4 particiones que contienen al menos un bloque de tamaño k=1. Con algún bloque de tamaño k=2 vemos que hay 3 y con tamaño k=3 solo hay una partición. Los de la primera columna son todas las 5 particiones para un conjunto con n=3 elementos, resultando que puede considerarse que todas las particiones contienen bloques con tamaño k=0, es decir, que cualquier partición puede incluir un bloque vacío y seguir siendo la misma partición.
En la siguiente tabla vemos los bloques para n=4:
| k=0 | k=1 | k=2 | k=3 | k=4 |
|---|---|---|---|---|
| abcd | abcd | |||
| abc.d | abc.d | abc.d | ||
| abd.c | abd.c | abd.c | ||
| ab.cd | ab.cd | |||
| ab.c.d | ab.c.d | ab.c.d | ||
| acd.b | acd.b | acd.b | ||
| ac.bd | ac.bd | |||
| ac.b.d | ac.b.d | ac.b.d | ||
| ad.bc | ad.bc | |||
| a.bcd | a.bcd | a.bcd | ||
| a.bc.d | a.bc.d | a.bc.d | ||
| ad.b.c | ad.b.c | ad.b.c | ||
| a.bd.c | a.bd.c | a.bd.c | ||
| a.b.cd | a.b.cd | a.b.cd | ||
| a.b.c.d | a.b.c.d | |||
| 15 | 11 | 9 | 4 | 1 |
Encontramos estas secuencias 5, 4, 3, 1 para n=3 y 15, 11, 9, 4, 1 para n=4 en la página OEIS A327884, donde define primero una recurrencia auxiliar que es precisamente sB(n, k) para las particiones con semi bloques, que se declara recursivamente así:
n>0 ⇒ sB(n, k) = ∑j=1..n (1 - δj,k) C(n-1, j-1) sB(n-j, k)
Recuerde que los Números de Bell tenían por recurrencia alternativa B(0) = 1, B(n) = ∑j=1..n C(n-1, j-1) B(n-j), que es similar a la anterior si omitimos k y el Delta de Kronecker que se define así:
| δi, j = { | 0 | si i≠j |
| 1 | si i=j |
Por lo tanto cuando j=k ⇒ 1 - δj,k = 0 y cuando j≠k ⇒ 1 - δj,k = 1
Usando la recurrencia anterior sB(n, k) define OEIS la expresión para calcular el valor numérico de pB(n, k) para las particiones con bloques parciales:
k>0 ⇒ pB(n, k) = sB(n, 0) - sB(n, k)
Se observa que si pB(n, k) son las particiones con bloques de tamaño k, la otra recurrencia sB(n, k) son todas las particiones menos las que contengan bloques de tamaño k, pues se observa que pB(n, 0) = sB(n, 0) = B(n)
Usando el algoritmo semiBell(n, k) calculamos el valor numérico de sB(n, k):
| n↓k→ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 |
| 3 | 5 | 1 | 2 | 4 | 5 | 5 | 5 | 5 | 5 |
| 4 | 15 | 4 | 6 | 11 | 14 | 15 | 15 | 15 | 15 |
| 5 | 52 | 11 | 17 | 32 | 47 | 51 | 52 | 52 | 52 |
| 6 | 203 | 41 | 53 | 113 | 173 | 197 | 202 | 203 | 203 |
| 7 | 877 | 162 | 205 | 422 | 702 | 835 | 870 | 876 | 877 |
| 8 | 4140 | 715 | 871 | 1788 | 3125 | 3860 | 4084 | 4132 | 4139 |
Usando el algoritmo partialBell(n, k) calculamos el valor numérico de pB(n, k), donde se observan las secuencias 5, 4, 3, 1 para n=3 y 15, 11, 9, 4, 1 para n=4 que vimos antes:
| n↓k→ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 2 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 5 | 4 | 3 | 1 | 0 | 0 | 0 | 0 | 0 |
| 4 | 15 | 11 | 9 | 4 | 1 | 0 | 0 | 0 | 0 |
| 5 | 52 | 41 | 35 | 20 | 5 | 1 | 0 | 0 | 0 |
| 6 | 203 | 162 | 150 | 90 | 30 | 6 | 1 | 0 | 0 |
| 7 | 877 | 715 | 672 | 455 | 175 | 42 | 7 | 1 | 0 |
| 8 | 4140 | 3425 | 3269 | 2352 | 1015 | 280 | 56 | 8 | 1 |
Se observa que pB(n, 0) = sB(n, 0) = B(n) obteniéndose la secuencia 1, 1, 2, 5, 15, 52, 203, ... de los números de Bell que ya vimos en un tema anterior. Además para k=1..n se cumple pB(n, 0) = sB(n, 0) = sB(n, k) + pB(n, k) tal como expone la recurrencia de pB(n, k)
Implementamos el algoritmo para calcular el valor numérico de sB(n, k) en la aplicación con el algoritmo semiBell(n, k):
// sB(n, k) = sum_(j=1)^(n) (j=k) (1-δ_(j,k)) sB(n-j, k) C(n-1, j-1)
function semiBell(n, k) {
if (n===0) {
return 1;
} else {
let sum = 0;
for (let j=1; j<=n; j++) {
if (j!==k) {
sum += semiBell(n-j, k) * binomial(n-1, j-1)
}
}
return sum;
}
Se observa que si j===k no sumamos en el bucle, que es la forma de implementar aquí el Delta de Kronecker visto. Y el algoritmo que calcula el valor numérico de pB(n, k) en la aplicación con el algoritmo partialBell(n, k):
// pB(n, k) = sB(n, 0) - sB(n, k)
function partialBell(n=0, k=0) {
let result = semiBell(n, 0);
if (k>0) result -= semiBell(n, k);
return result;
}Algoritmo para generar particiones con semi bloques
El primer algoritmo para generar las particiones con semi bloques lo haremos basándonos en el algoritmo partition3(list) que usaba el algoritmo combineComplement2(list, k) para obtener a la vez las combinaciones y sus complementarias de una lista.
// sB(n, k) = sum_(j=1)^n (1-δ_(j,k)) C(n-1, j-1) sB(n-j, k)
function semiPartition1(list=[], k=0){
let n = list.length;
let result = []
if (n===0) {
//iter += 1;
result.push([]);
} else {
//iter += 1;
let pivot = list[0];
//iter += (n-1);
let subList = list.slice(1);
for (let j=1; j<=n; j++) {
//iter += 1;
if (j!==k) {
let c = combineComplement2(subList, j-1);
/* c.length = C(n-1, j-1 */
for (let i=0; i<c.length; i++) {
//iter += 1;
let [combination, complement] = c[i];
/* combination.length = j-1 */
/* complement.length = n-1-(j-1) = n-j */
//iter += combination.length;
let pc = [pivot, ...combination];
let p = semiPartition1(complement, k);
/* p.length = semiBell(n-j, k) */
for (let m=0; m<p.length; m++) {
//iter += 1;
p[m].push(pc);
result.push(p[m]);
}
}
}
}
}
return result;
}Se basa en la fórmula recurrente para obtener las particiones con semi bloques que hemos visto más arriba:
n>0 ⇒ sB(n, k) = ∑j=1..n (1 - δj,k) C(n-1, j-1) sB(n-j, k)
El desglose del coste es parecido al que hicimos para el algoritmo partition3(list):
T(n, k) = 1 + (n-1) + ∑j=1..n ( 1 + (1-δj, k) ( Tcc(n-1, j) + C(n-1, j-1) ×
( 1 + (j-1) + T(n-j, k) + sB(n-j, k) × 1 ) )
que simplificando queda la parte recursiva:
C(n-1, j-1) j + C(n-1, j) ( T(n-j, k) + sB(n-j, k) ) ) )
Aplicando sumatorios a algunos de los términos:
- ∑j=1..n 1 = n
- ∑j=1..n (1-δj, k) C(n-1, j) j = (n+1) 2n-2 - C(n-1, k) k
Con lo que llegamos finalmente a esta fórmula final para el coste de semiPartition1(list, k)
T(n, k) = 2n + (n+1) 2n-2 - C(n-1, k-1) k +
∑j=1..n (1 - δj,k) ( Tcc(n-1, j-1) + C(n-1, j-1) ( sB(n-j, k) + T(n-j, k) ) )
Donde sB(n, k) son las particiones con semi bloques parciales (o semi Bell) que ya comentamos antes. Y Tcc(n, k) son las combinaciones complementarias del algoritmo combineComplement2(n, k) para lo que no he encontrado una fórmula cerrada:
t(n, k) = n + C(n, k) - 1 + t(n-1, k-1) + t(n-1, k)
T(n, k) = t(n, k) + n + k + n C(n, k)
En caso de coste de copia sólo hay que agregar lo resaltado en amarillo.
Algoritmo para generar particiones con bloques parciales
Vimos que las particiones con bloques parciales pB(n, k) se calculan restando a las particiones totales B(n) = pB(n, 0) las particiones con semi bloques sB(n, k). Para encontrar un algoritmo parecido vamos a generar todas las particiones con el algoritmo partition4(list) que usaba los números de Stirling de segunda clase y, luego, realizamos un filtrado para quedarnos sólo con aquellas que tengan bloques de longitud k:
// pB(n) = B(n) - sB(n, k)
function partialPartition1(list=[], k=0) {
iter += 1;
let result = [];
if (k<=list.length) {
let res = partition4(list);
// particiones totales = res.length = B(n)
for (let i=0; i<res.length; i++) {
iter += 1;
// num bloques de un partición = res[i].length
for (let j=0; j<res[i].length; j++){
iter += 1;
// elementos en un bloque = res[i][j].length
if (k===0 || res[i][j].length===k) {
result.push(res[i]);
break;
}
}
}
}
return result;
}Para analizar el coste vamos a ignorar de momento la sentencia break. Vemos que el coste incluye el del algoritmo partition4(list) que ya conocemos y que denominaremos Tp(n). Genera ese algoritmo B(n) particiones, por lo que el coste será algo como, lo que sigue, siendo M(n) el número medio de bloques por partición:
n≥k ⇒ T(n, k) = Tp(n) + B(n) × (1 + M(n) × 1)
Para calcular M(n) recordemos que una partición de un conjunto con n elementos tiene entre uno y n subconjuntos o bloques. Por ejemplo, las particiones con el conjunto de partida {a, b, c} son abc, ab.c, ac.b, a.bc, a.b.c de forma compacta, donde hay 1 partición que tiene 1 bloque, luego hay 3 particiones con 2 bloques ab.c, ac.b, a.bc y finalmente 1 partición con 3 bloques a.b.c. Si designamos N(n) el número de bloques en todas las particiones, en total hay N(3) = 1 × 1 + 3 × 2 + 1 × 3 = 1 + 6 + 3 = 10
Para contar todos los bloques que hay en todas las particiones recordamos lo que vimos en Particiones parciales, donde exponíamos esta tabla para n=3:
| list | n | k | kPartition(list, k) | S2(n, k) |
|---|---|---|---|---|
| [a, b, c] | 3 | 0 | ∅ | S2(3, 0) = 0 |
| 1 | [[a, b, c]] | S2(3, 1) = 1 | ||
| 2 | [[a, b], [c]] [[a, c], [b]] [[a], [b, c]] | S2(3, 2) = 3 | ||
| 3 | [[a], [b], [c]] | S2(3, 3) = 1 |
Si contamos los subconjuntos o bloques vemos que hay 10, pues obedece a esta fórmula:
Si hay B(n) particiones, entonces el número medio de bloques por partición es:
| M(n) = | N(n) | = | ∑j=0..n j S2(n, j) |
| B(n) | B(n) |
Incluyendo M(n) en la fórmula del coste de más arriba llegamos a:
Ese coste es el que obtenemos si no incluyéramos la sentencia break. En otro caso si una función desconocida es 0 < f(n, k) ≤ 1, el coste incluyendo break será algo como esto:
Dado que no pude encontrar f(n, k), al menos podemos asegurar que el coste de partialPartition1(n, k) se acota superiormente cuando consideramos la sentencia break así:
n≥k ⇒ T(n, k) ≤ 1 + Tp(n) + B(n) + ∑j=0..n j S2(n, j)
En caso de omitir break el coste es exactamente igual que esa expresión, no dependiente de k. Recordemos que Tp(n) era:
donde agregábamos lo resaltado en caso de coste con copia.