El algoritmo vuelta atrás para resolver el Sudoku

El algoritmo recursivo de vuelta atrás (backtracking) tiene por objetivo recorrer una estructura de árbol para encontrar uno o más nodos que cumplan determinados requisitos. En el tema sobre recursivos vuelta atrás expuse algunos ejemplos de uso. Es adecuado para resolver un Sudoku, donde podemos asimilar cada combinación posible de números en el tablero como un nodo del árbol.

En el tema anterior vimos una aplicación de gestión de Sudokus donde usamos este algoritmo para resolverlos. En este tema vamos a exponer y comentar el algoritmo del vuelta atrás utilizado. Pongamos aquí un ejemplo para ver el resultado:

El algoritmo vuelta atrás básico que busca todas las posibles soluciones en un determinado árbol relacionado con un problema genérico es el siguiente:

function resolver(nodoInicial){
    let nodoVacio = crear(nodoInicial);
    let soluciones = [];
    function vueltaAtras(nodo){
        if (esSolucion(nodo)){
            guardar(nodo, soluciones);
        }
        for (let complecion of buscarCompleciones(nodo)) {
            if (acotar(nodo, complecion)) {
                probar(nodo, complecion);
                vueltaAtras(nodo);
                deshacer(nodo);
            }
        }
    }
    resolver(nodoVacio);
    return soluciones;
}

Un nodo es, por ejemplo, un tablero Sudoku con una combinación de números en algunas o todas las celdas. Cuando se completen todas las celdas tendremos una solución. Esto lo comprobamos con la función auxiliar esSolucion(nodo). El algoritmo recorre todas las posibles combinaciones devolviendo todas las soluciones. Buscar las compleciones de un nodo sería, en el caso del Sudoku, seleccionar la primera celda vacía y obtener los números disponibles que podemos usar en esa celda. La variable complecion podría ser un Array con las posiciones de la celda y el número disponible, algo como [i, j, n].

La función acotar(nodo, complecion) nos dirá si es posible usar ese número disponible en esa celda, para lo cual comprobaremos que se cumplen algún criterio o restricción que imponga el problema. En caso verdadero insertamos con probar(nodo, complecion) ese valor en el nodo y volvemos a ejecutar recursivamente el vuelta atrás. Cuando el recursive finalice una bajada, se deshace esa inserción con deshacer(nodo) y se prueba el siguiente disponible. De esta forma este algoritmo recorre todas las combinaciones posibles encontrando todas las soluciones.

Lo anterior es una idea general de como funciona un vuelta atrás. Cada problema tendrá su particularidades, pero lo anterior puede ayudar a entender el árbol implícito que hay detrás de un recursivo vuelta atrás, como veremos a continuación.

El árbol del vuelta atrás que resuelve el Sudoku

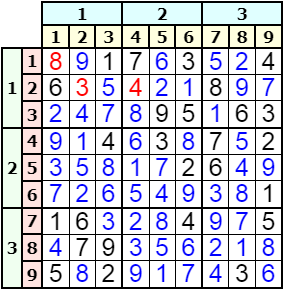
El ejemplo del apartado anterior se resuelve obteniendo la solución que se muestra en la Figura. Los números en color negro son los iniciales (clues en terminología al uso sobre Sudokus). En color rojo son los que se obtienen del vuelta atrás. Los azules son los de la ejecución del profundizado usando una función auxiliar profundizar(nodo), acción que se ejecuta dentro de la función acotar(). Y también antes de iniciar el recursivo. Luego explicaremos algo más sobre esto. Así como conviene también ver el apartado sobre el profundizado del tema que expone la aplicación para gestionar Sudokus. En el apartado final de este tema también se comentan más cosas.

Nunca es fácil trazar un recursivo. Y menos el vuelta atrás de este algoritmo que resuelve un Sudoku. No sé si lo que sigue quedará expuesto de una forma que se entienda. Lo importante es no olvidar que el vuelta atrás recorre un árbol implícito encontrando aquellas hojas que son solución del problema. El árbol realmente no existe como estructura. Es la acción del recursivo lo que conforma ese árbol.

El ejemplo nos muestra una traza del estado del tablero en cada iteración:

iter=0 i=0 j=0 n=""
* * 1 7 6 3 5 2 4
6 * * * * 1 8 * *
* * 7 8 9 5 1 6 3
* * 4 * 3 * 7 * 2
* * * * * 2 6 * *
* * 6 * * * 3 * 1
1 6 * * * 4 * * 5
* 7 9 * * * * 1 *
5 * 2 * * * * 3 *

iter=1 i=1 j=1 n=8
8 9 1 7 6 3 5 2 4
6 * * * * 1 8 * *
* * 7 8 9 5 1 6 3
9 * 4 * 3 * 7 * 2
* * * * * 2 6 * *
* * 6 * * * 3 * 1
1 6 * * * 4 * * 5
* 7 9 * * * * 1 *
5 * 2 * * * * 3 *

iter=2 i=2 j=2 n=3
8 9 1 7 6 3 5 2 4
6 3 5 * * 1 8 * *
* * 7 8 9 5 1 6 3
9 * 4 * 3 * 7 * 2
* * * * * 2 6 * *
* * 6 * * * 3 * 1
1 6 * * * 4 * * 5
* 7 9 * * * * 1 *
5 * 2 * * * * 3 *

iter=3 i=2 j=4 n=2
8 9 1 7 6 3 5 2 4
6 3 5 2 4 1 8 * *
* * 7 8 9 5 1 6 3
9 * 4 * 3 * 7 * 2
* * * * * 2 6 * *
* * 6 * * * 3 * 1
1 6 * * * 4 * * 5
* 7 9 * * * * 1 *
5 * 2 * * * * 3 *

FALLIDO iter=4 i=2 j=8 n=7
8 9 1 7 6 3 5 2 4
6 3 5 2 4 1 8 * *
* * 7 8 9 5 1 6 3
9 * 4 * 3 * 7 * 2
* * * * * 2 6 * *
* * 6 * * * 3 * 1
1 6 * * * 4 * * 5
* 7 9 * * * * 1 *
5 * 2 * * * * 3 *

iter=4 i=2 j=8 n=9
8 9 1 7 6 3 5 2 4
6 3 5 2 4 1 8 9 7
* * 7 8 9 5 1 6 3
9 * 4 * 3 * 7 * 2
* * * * * 2 6 * 9
* * 6 * * * 3 * 1
1 6 * * * 4 * 7 5
* 7 9 * * * * 1 *
5 * 2 * * * * 3 *

FALLIDO iter=5 i=3 j=1 n=2
8 9 1 7 6 3 5 2 4
6 3 5 2 4 1 8 9 7
* * 7 8 9 5 1 6 3
9 * 4 * 3 * 7 * 2
* * * * * 2 6 * 9
* * 6 * * * 3 * 1
1 6 * * * 4 * 7 5
* 7 9 * * * * 1 *
5 * 2 * * * * 3 *

FALLIDO iter=5 i=3 j=1 n=4
8 9 1 7 6 3 5 2 4
6 3 5 2 4 1 8 9 7
* * 7 8 9 5 1 6 3
9 * 4 * 3 * 7 * 2
* * * * * 2 6 * 9
* * 6 * * * 3 * 1
1 6 * * * 4 * 7 5
* 7 9 * * * * 1 *
5 * 2 * * * * 3 *

iter=5 i=2 j=4 n=4
8 9 1 7 6 3 5 2 4
6 3 5 4 2 1 8 9 7
2 4 7 8 9 5 1 6 3
9 1 4 6 3 8 7 5 2
3 5 8 1 7 2 6 4 9
7 2 6 5 4 9 3 8 1
1 6 3 2 8 4 9 7 5
4 7 9 3 5 6 2 1 8
5 8 2 9 1 7 4 3 6

FALLIDO iter=6 i=2 j=2 n=5
8 9 1 7 6 3 5 2 4
6 * * * * 1 8 * *
* * 7 8 9 5 1 6 3
9 * 4 * 3 * 7 * 2
* * * * * 2 6 * *
* * 6 * * * 3 * 1
1 6 * * * 4 * * 5
* 7 9 * * * * 1 *
5 * 2 * * * * 3 *

FALLIDO iter=6 i=1 j=1 n=9
* * 1 7 6 3 5 2 4
6 * * * * 1 8 * *
* * 7 8 9 5 1 6 3
* * 4 * 3 * 7 * 2
* * * * * 2 6 * *
* * 6 * * * 3 * 1
1 6 * * * 4 * * 5
* 7 9 * * * * 1 *
5 * 2 * * * * 3 *

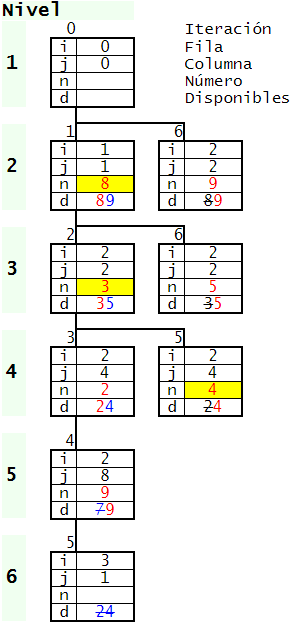
En la Figura se observa el árbol implícito del algoritmo. Volvemos a repetir que este árbol no existe como estructura. Cada nodo es la representación interna de una iteración del recursivo vuelta atrás y representa un tablero en cada momento. En el código vemos que la función recursiva es vueltaAtras(nodo), donde nodo es un objeto que guarda el tablero (un Array de dos dimensiones) y otras cosas, como veremos en siguientes apartados. Ese nodo se va pasando por referencia entre funciones y siempre es el mismo tablero que vamos llenado hasta, finalmente, completarlo.

En la traza los valores i, j son los de la posición de cada celda y se enumeran desde 1. Así por ejemplo, la primera celda en la posición superior izquierda sería la [1, 1], aunque en el código JavaScript lo hagan desde cero, siendo en este caso la posición [0, 0] en el Array de dos dimensiones que almacena un tablero.

Al inicio la primera fila es * * 1 7 * 3 * * 4, donde los asteriscos son celdas vacías. Aplicamos un primer profundizado antes de entrar en el recursivo quedando * * 1 7 6 3 5 2 4. Esta es la situación en el nivel 1 e iteración 0 de la Figura, antes de entrar en la iteración 1. Observe que el profundizado encontró los números 6, 5 y 2 (en color azul).

En el nivel 2 buscamos la primera celda vacía resultando ser la primera del tablero. Tiene como disponibles los números 8 y 9. Probamos el primero, el número 8, reflejándose estos valores con i=1 j=1 n=8 d=89 en la Figura (nivel 2 iteración 1). Insertando ese número queda la primera fila con los números 8 9 1 7 6 3 5 2 4. Marcamos en rojo el número seleccionado por el vuelta atrás. Al ejecutar en ese momento el profundizado vuelve a encontrar otros números, completándose esa primera fila.

En el paso anterior la segunda fila quedó como sigue 6 * * * * 1 8 * *. Por lo tanto dado que la primera fila está completa, la siguiente celda vacía es la segunda de esta segunda fila. En la Figura (nivel 3, iteración 2) vemos que se selecciona i=2 j=2 n=3 d=35, tras lo cual la segunda fila queda 6 3 5 * * 1 8 * *. Pasamos a la siguiente casilla vacía, la cuarta de esa fila i=2 j=4 n=2 d=24 (nivel 4, iteración 3), quedando ahora esa segunda fila 6 3 5 2 4 1 8 * *, encontrándose nuevamente otro número más con el profundizado, el número 4.

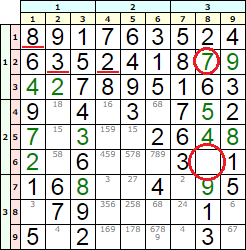
La siguiente casilla sigue estando en la segunda fila, en i=2 j=8 n=9 d=79 (nivel 5, iteración 4). Observe que el número 7 de los disponibles aparece tachado para indicar que fue fallido cuando se ejecutó el profundizado tras probar ese número. Eso quiere decir que la inserción del 7 condujo el tablero a un estado en que no puede completarse. Decimos que es no completable porque en la ejecución del profundizado llegamos a tener una celda sin números disponibles, como se observa en la Figura que sucede con la celda [6, 8] tras insertar el 7 en la celda [2, 8]. Esa imagen procede de la aplicación de gestión de Sudokus, donde los números disponibles (o pencil marks en terminología sobre Sudokus en inglés) se presentan con una lista de números más pequeños en cada celda vacía.

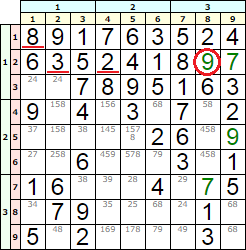
Si de los disponibles 7 y 9 el primero resultó fallido, pasamos a probar el 9, quedando la fila segunda como sigue 6 3 5 2 4 1 8 9 7. Seguimos estando en i=2 j=8 n=9 d=79 (nivel 5, iteración 4) del árbol. Como se observa en la Figura, tras insertar el número 9 en la celda [2, 8] y aplicar el profundizado se obtiene el 7 en esa fila y algunos números más en otras filas (los de color verde en la Figura).

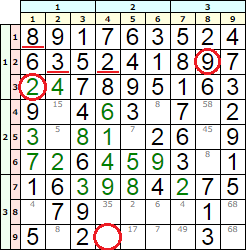
Tal como se observa en la Figura, seguimos probando con el vuelta atrás el número disponible 2 en la siguiente celda [3, 1] llegando a un estado no completable, pues la celda [9, 4] se queda sin disponibles. Lo mismo pasa si probamos con el 4 en esa celda [3, 1] quedando sin disponibles la celda [9, 7]. Entonces el número 9 de la celda [2, 8] será rechazado pues esa rama del árbol no ofrece solución. Diferenciamos entre rechazado y fallido, pues el fallido proviene de la ejecución del profundizado, mientras que el rechazado proviene de la ejecución de los números que se prueban en el vuelta atrás.

Esto significa que hay que hacer una vuelta atrás desde el número 9 en la celda [2, 8] hasta un nodo del árbol anterior donde tengamos otro disponible que usar para ver si se completa el tablero. Ese nodo inmediatamente anterior está en el nivel 4 e iteración 3. Seleccionamos i=2 j=4 n=4 d=24 en el nivel 4 e iteración 5, donde antes probamos el 2 y ahora probaremos el 4. Nos conduce ahora la segunda fila al resultado final 6 3 5 4 2 1 8 9 7 y produciendo un tablero que se rellena totalmente con el profundizado y, por tanto, primera solución del Sudoku.

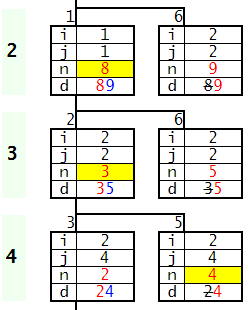
En la Figura podemos ver el detalle del árbol donde se bifurca una nueva rama en el nivel 4, iteración 5, conduciendo a una primera solución final que completa el tablero con los números resaltados en amarillo 8, 3 y 4 encontrados con el vuelta atrás. El algoritmo continuará buscando más soluciones. Por eso hace un nuevo vuelta atrás al nodo anterior en el nivel 3 para probar el número 5 de sus disponibles 3 y 5. No conduce a una solución por lo que vuelve atrás al nodo anterior para probar el segundo número 9 que tampoco ofrece una solución. Se acaban todas las combinaciones posibles y el algoritmo devuelve una única solución, con lo cual se puede asegurar que este Sudoku no tiene más soluciones.

Este Sudoku tiene un árbol de resolución bastante simple. En otros casos el árbol tiene más ramificaciones, muchas no conducen a un tablero completado ocasionando vueltas atrás hasta que, finalmente, encuentre una rama que si lo hace. O bien que se completen todas las combinaciones posibles y no encuentre solución alguna. Por otro lado el número de soluciones puede ser muy grande y conviene dotar de un mecanismo para no recorrerlas todas. Por eso hemos de proveer al algoritmo definitivo de limitaciones para un control de la ejecución. Esto lo veremos en el siguiente apartado.

Código del algoritmo vuelta atrás que resuelve el Sudoku

En lo que sigue presentamos el código del algoritmo vuelta atrás que resuelve el Sudoku. El código original contiene más instrucciones destinadas a mostrar resúmenes informativos y trazados que obviamos en lo que sigue para mejor legibilidad. Empezamos por la función principal, una particularización del código general que vimos en el primer apartado de este tema:

function resolverSudoku(tablero=[[]],numSoluciones=Infinity,maxIter=100}){
    let nodoVacio = crear(tablero);
    let tableros = [];
    let iter = 0;
    let numSolucion = 0;
    function resolver(nodo){
        iter++;
        if (esSolucion(nodo) || iter>=maxIter){
            if (esSolucion(nodo)) {
                tableros = guardar(nodo, tableros);
                numSolucion++;
            }
            return numSolucion===numSoluciones || iter>=maxIter;
        } else {
            let [i, j, d] = buscarSiguienteCasillaVacia(nodo);
            if (d!=="") {
                for (let k=0; k<d.length; k++) {
                    let n = d[k];
                    if (acotar(nodo, i, j, n)) {
                        probar(nodo, i, j, n);
                        if (resolver(nodo)) return true;
                        deshacer(nodo);
                    }
                }
            }
            return false;
        }
    }
    profundizar(nodoVacio);
    resolver(nodoVacio);
    return tableros;
}

La función resolverSudoku(tablero, numSoluciones, maxIter) recibe un Array de dos dimensiones con los números iniciales (o clues en inglés) del tablero, un argumento para limitar el número de soluciones a devolver y otro para limitar el máximo de iteraciones. Por defecto se devuelven todas las soluciones usando el valor Infinity. Pero si se llega al máximo de iteraciones el algoritmo se detiene devolviendo las soluciones encontradas hasta ese momento.

El recursivo es la función interna resolver(nodo). Externamente creamos un nodo vacío con la función crear(tablero) y a continuación ejecutamos resolver(nodoVacio). Las variables iter, tableros, numSolucion son globales al recursivo. La variable tableros es un Array donde se van guardando las soluciones encontradas. Observe como se estructura el código con funciones auxiliares que ayudan a concentrarnos en lo principal. Veamos la primera que encontramos crear(tablero):

function crear(tablero){
    let nodo = {
        numeros: Array.from({length:9}, (v,i)=>Array.from({length: 9}, 
            (w,j) => tablero[i][j])),
        disponibles: Array.from({length:9}, (v,i)=>Array.from({length: 9}, 
            (w,j) => tablero[i][j]?"":buscarDisponibles(tablero, i, j))),
        prueba: {numeros: [], disponibles: []},
        bak: {numeros: [], disponibles: []}
    };
    return nodo;
}

Con esta función creamos un nodo vacío que es un objeto con una copia del Array de números existentes en el tablero en ese momento inicial y otro con los disponibles en cada celda. En las entradas prueba y bak guardamos el estado en la función acotar() y probar() respectivamente. Con bak recuperamos el tablero anterior en la función auxiliar deshacer() en el caso de que esa prueba no resulte satisfactoria. Vease que el nodo en cualquier momento es un objeto como el siguiente:

nodo = {
    numeros:  [[]],
    disponibles: [[]],
    prueba: {
        numeros: [[]],
        disponibles: [[]],
    },
    bak: {
        numeros: [[]],
        disponibles: [[]],
    }
}

El mismo nodo creado inicialmente se va pasando entre funciones por referencia, por lo que no es necesario devolverlo expresamente en cada función. Aunque hablamos de un árbol de nodos, realmente el algoritmo trabaja siempre con la misma estructura. Veamos buscarDisponibles():

function buscarDisponibles(tablero=[[]], i=0, j=0){
    let fila = tablero[i];
    let columna = tablero.map(v => v[j]);
    let [ci, cj] = [Math.trunc(i/3), Math.trunc(j/3)];
    let caja = [];
    tablero.forEach((v, ii) => {
        if (Math.trunc(ii/3)===ci){
            caja.push(v.filter((w, jj) => Math.trunc(jj/3)===cj));
        }
    });
    caja = caja.flat();
    let disponibles = [..."123456789"].filter(v => !fila.includes(v) &&
        !columna.includes(v) && !caja.includes(v))
    return disponibles.join("");
}

La función busca los números disponibles en la celda i, j de un tablero. Extraemos la fila, columna y caja correspondiente donde se ubique esa celda. Los números disponibles para esa celda serán aquellos que no se encuentren en esa fila, columna y caja.

En cada iteración del recursivo comprobamos si el tablero en ese momento es una solución, en cuyo caso la guardamos:

function esSolucion(nodo){
    return nodo.numeros.every(v => v.every(w => w!==""));
}
function guardar(nodo, tableros) {
    tableros.push([...nodo.numeros]);
    return tableros;
}

Poco hay que decir de las funciones anteriores. La primera comprueba que todas las celdas del tablero están llenas. La segunda guarda esa solución en la variable global tableros.

Probando números en el vuelta atrás

Para explicar el resto de funciones auxiliares volvemos a repetir aquí la parte del recursivo que se encarga de probar números hasta conseguir las soluciones:

...
    let [i, j, d] = buscarSiguienteCasillaVacia(nodo);
    if (d!=="") {
        for (let k=0; k<d.length; k++) {
            let n = d[k];
            if (acotar(nodo, i, j, n)) {
                probar(nodo, i, j, n);
                if (resolver(nodo)) return true;
                deshacer(nodo);
            }
        }
    }
    return false;
...
    

Si el tablero en una iteración no es solución entonces buscamos la siguiente celda (o casilla) vacía:

function buscarSiguienteCasillaVacia(nodo){
    let casilla = [-1, -1, ""];
    for (let i=0; i<9; i++){
        for (let j=0; j<9; j++){
            if (nodo.numeros[i][j]===""){
                return [i, j, nodo.disponibles[i][j]];
            }
        }
    }
    return casilla;
}

La función anterior es simple, se limita a iterar por todas las celdas empezando en la primera superior izquierda hasta encontrar una vacía. Esta es una búsqueda del tipo "siguiente". En el código original tenemos la posibilidad de realizar búsquedas por tipo "mínimo" o "aleatorio". Con el tipo mínimo buscaríamos la celda que menos disponibles tenga. Con la opción aleatoria buscamos una celda aleatoriamente entre las que tengan disponibles, o lo que es lo mismo, entre las celdas vacías.

La búsqueda de la siguiente celda vacía nos devuelve el Array [i, j, d], siendo d un String con los números disponibles. Iteramos por esos números para probar si completan una solución usando la función acotar(nodo, i, j, n), que hace uso de las auxiliares llenar(nodo, i, j, n) y borrarDisponibles(nodo, i, j, n):

function llenar(nodo, i, j, n){
    nodo.numeros[i][j] = n;
    nodo.disponibles[i][j] = "";
}

function borrarDisponibles(nodo, i, j, n){
    let [ci, cj] = [Math.trunc(i/3), Math.trunc(j/3)];
    for (let ii=0; ii<9; ii++){
        for (let jj=0; jj<9; jj++){
            if (nodo.numeros[ii][jj]==="" && (ii===i || jj===j || 
                    Math.trunc(ii/3)===ci && Math.trunc(jj/3)===cj)){
                nodo.disponibles[ii][jj] = nodo.disponibles[ii][jj].
                    replace(n, "");
                if (nodo.disponibles[ii][jj]==="") return false;
            }
        }
    }
    return true;
}

function acotar(nodo, i, j, n){
    nodo.prueba = {
        numeros: [...nodo.numeros].map(v => [...v]),
        disponibles: [...nodo.disponibles].map(v => [...v])
    };
    llenar(nodo.prueba, i, j, n);
    let completable = borrarDisponibles(nodo.prueba, i, j, n);
    if (completable){
        completable = profundizar(nodo.prueba);
    }
    return completable;
}

En acotar(nodo, i, j, n) hacemos una copia en nodo.prueba e insertamos el número n con llenar(nodo.prueba, i, j, n). A continuación borramos los disponibles que no es otra cosa que borrar la aparición de ese número en la fila, columna y caja donde se ubica la celda i, j. Si en ese borrado aparece alguna celda vacía sin disponibles es indicativo de que ese tablero no es completable. En otro caso procedemos a ejecutar profundizar(nodo.prueba), acción de profundizar en el árbol que comentaremos en un siguiente apartado. Ese profundizado, además de descubrir más números, devolverá también si el tablero es o no completable.

En el recursivo vemos que si el resultado de acotar() produce un tablero completable devolviendo verdadero, entonces podemos probar definitivamente ese número:

...
    if (acotar(nodo, i, j, n)) {
        probar(nodo, i, j, n);
        if (resolver(nodo)) return true;
        deshacer(nodo);
    }
...

Tras probar el número llamamos nuevamente al recursivo para seguir el curso de la ejecución con ese nuevo tablero. En caso de que esa nueva llamada no devuelva una solución pasamos a deshacer la última acción. Estás son las funciones auxiliares que entran en juego en esta parte del recursivo:

function guardarBak(nodo) {
    nodo.bak.numeros.push([...nodo.numeros].map(v => [...v]));
    nodo.bak.disponibles.push([...nodo.disponibles].map(v => [...v]));
}

function probar(nodo, i, j, n){
    guardarBak(nodo);
    nodo.numeros = [...nodo.prueba.numeros].map(v => [...v]);
    nodo.disponibles = [...nodo.prueba.disponibles].map(v => [...v]);
}

function deshacer(nodo){
    nodo.numeros = nodo.bak.numeros.pop();
    nodo.disponibles = nodo.bak.disponibles.pop();
}

Al probar guardamos en la propiedad bak del nodo una copia del mismo. Probamos el número simplemente trasladando lo que pusimos en nodo.prueba dentro de la función acotar(). Deshacemos recuperando la copia desde bak.

Profundizando en el árbol del Sudoku

La acción de profundizar se refiere a aplicar las técnicas de resolución de un Sudoku con solución única sin usar vuelta atrás. El objetivo principal de este juego sería resolverlo sin vuelta atrás, pues al fin y al cabo no deja de ser más que un método de fuerza bruta que siempre consigue resolver el Sudoku. El término se refiere a profundizar en el árbol de resolución del vuelta atrás. Sin estas acciones el árbol resultará mucho más extenso, por lo que aplicar el profundizado nos acorta las ramas hasta las soluciones.

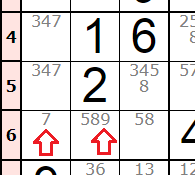
Hay muchas técnicas de profundizado. Y no siempre son fáciles de aprender. Pero sólo hay dos técnicas básicas que nos ayudan a encontrar nuevos números: únicos solitarios y únicos ocultos (naked singles y hidden singles). En la Figura se observa parte de un Sudoku, presentando una de sus cajas (box) que es un rectángulo de 3×3 celdas. Aparecen los números disponibles en cada celda. El número 7 es un solitario único pues es único en esa celda y lo podemos insertar. También tenemos el 9 en la celda contigua, que es un número solitario oculto en la caja, puesto que no hay más números 9 en esa caja. Podemos entonces insertar también ese 9 en esa celda.

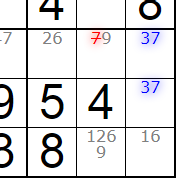
El resto de técnicas no descubren nuevos números sino que reducen los disponibles. En uno o más pasos posteriores esta reducción puede dar lugar a que aparezcan números únicos solitarios u ocultos. Por ejemplo, en la Figura se observa una pareja de solitarios (naked pair) en la última caja del tablero. Observamos que los números 3 y 7 resaltados en color azul sólo aparecen en dos celdas de esa caja, por lo que tienen que ir obligatoriamente en ellas, pudiendo eliminarse las apariciones de esos números en el resto de disponibles de esa caja. Eliminando el 7 que aparece tachado en color rojo observamos que nos va a quedar un 9 solitario único que podemos insertar en esa celda. La mayor parte de las veces estos números no se descubren en el mismo paso, pero al ir reduciendo los disponibles facilitarán su descubrimiento en pasos posteriores.

Las técnicas de profundizado que uso hasta el momento son: únicos solitarios y ocultos, parejas solitarias y ocultas, trios solitarios y ocultos, bloqueados, Ala X y Ala XY. En inglés se les denomina naked and hidden singles, naked and hidden pairs, naked and hidden trios, locked, X Wing, XY Wing.

Veamos ahora la función para profundizar en el árbol:

function profundizar(nodo}){
    let completable = true, i=-1, j=-1, n="", ok=false;
    do {
        [i, j, n, ok] = seleccionarDisponible(nodo);
        if (n!==""){
            llenar(nodo, i, j, n);
            completable = borrarDisponibles(nodo, i, j, n);
        }
    } while (ok && completable && !esSolucion(nodo));
    return completable;
}

Tenemos un bucle que selecciona un disponible usando las técnicas de profundizado con la función seleccionarDisponible(nodo) que veremos a continuación. Cuando se encuentre un solitario único u oculto con esa función, devolverá el Array [i, j, n, ok] con la posición i, j de la celda donde insertar el número n (un String). Para el resto de técnicas el Array será [-1, -1, "", true] si encontró alguna, producidendo el borrado de disponibles en la propia función seleccionarDisponible(nodo). Si no encuentra nada devolverá [-1, -1, "", false] detectándose en la variable ok.

Mientras se encuentre una técnica, es decir, mientras ok sea verdadero, el bucle seguirá buscando. Si encontró un número n lo insertará en la celda con llenar(nodo, i, j, n) y a continuación borrará los disponibles en la fila, columna y caja correspondiente. Esta acción puede hacer que aparezca una celda vacía de disponibles con lo que el Sudoku no será completable. Esta variable también se detecta para detener el bucle y, a la vez, es la que se devuelve en la función. También se detiene si se completa el Sudoku, lo que se comprueba con esSolucion(nodo).

La función que selecciona disponibles es la siguiente:

function seleccionarDisponible(nodo) {
    let ok = false;
    // Números únicos en una celda (Naked singles)
    for (let i=0; i<9; i++){
        for (let j=0; j<9; j++){
            if (nodo.disponibles[i][j].length===1){
                return [i, j, nodo.disponibles[i][j], true];
            }
        }
    }
    //Números únicos en una fila  (Hidden singles)
    for (let i=0; i<9; i++){
        for (let n=1; n<10; n++){
            let nn = n.toString();
            let cuenta = 0;
            let columna = -1;
            for (let j=0; j<9; j++){
                if (nodo.disponibles[i][j].includes(nn)) {
                    cuenta++;
                    columna = j;
                    if (cuenta>1) break;
                }
            }
            if (cuenta===1) {
                return [i, columna, nn, true];
            }
        }
    }
    //... siguen resto de acciones de profundizado
    return [-1, -1, "", ok];
}

En el código anterior sólo presentamos la búsqueda de Naked singles y de Hidden singles en filas. En el código original siguen los bucles para aplicar el resto de técnicas. Generalmente por cada técnica hay un bucle para filas, otro para columnas y otro más para cajas. Una de las consideraciones sobre la eficiencia a tener en cuenta tiene que ver con estos bucles. Hay que aplicarlos para cada técnica, puesto que la forma de buscarlos es diferente para cada una. Cuanto más técnicas se usen con mayor facilidad resolveremos un Sudoku sin tener que aplicar vuelta atrás. Pero también más tiempo tarda en recorrer todos esos bucles.