Unicidad de un Sudoku (Uniqueness)

Un verdadero Sudoku es aquel tablero inicial que conduce a una única solución. Muchos tableros iniciales conducen a resultados con más de una solución. E incluso algunos no tienen solución. El problema de resolver un Sudoku con técnicas de profundizado y sin usar el último recurso del vuelta atrás parte de la base de que el tablero inicial conduce a una única solución. Y esto puede aprovecharse para crear un nuevo conjunto de técnicas que se agrupan dentro del termino Unicidad (Uniqueness).

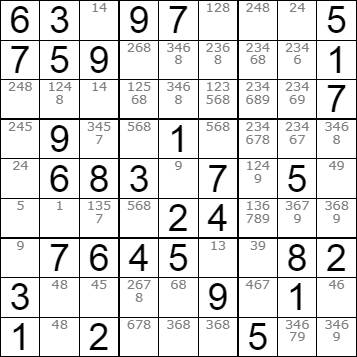
Para explicar el concepto de unicidad de un Sudoku (uniqueness of a Sudoku) creamos el tablero inicial de la Figura que se resuelve con dos soluciones:

Solución 1:
6 3 1 9 7 8 4 2 5
7 5 9 6 4 2 8 3 1
8 2 4 1 3 5 6 9 7
4 9 3 5 1 6 2 7 8
2 6 8 3 9 7 1 5 4
5 1 7 8 2 4 9 6 3
9 7 6 4 5 1 3 8 2
3 4 5 2 8 9 7 1 6
1 8 2 7 6 3 5 4 9

Solución 2:
6 3 1 9 7 8 4 2 5
7 5 9 6 4 2 8 3 1
8 2 4 1 3 5 9 6 7
4 9 3 5 1 6 2 7 8
2 6 8 3 9 7 1 5 4
5 1 7 8 2 4 6 9 3
9 7 6 4 5 1 3 8 2
3 4 5 2 8 9 7 1 6
1 8 2 7 6 3 5 4 9

Observe los cuatro números resaltados, cuya alternancia conduce a esas dos soluciones.

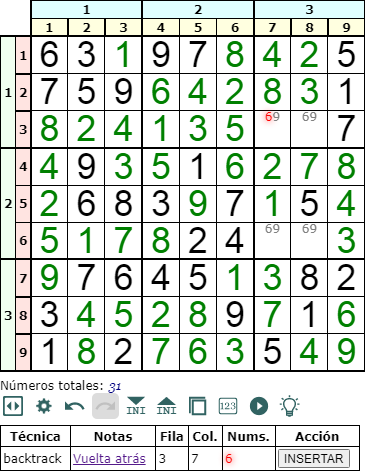
Si usamos el tablero inicial anterior en el gestor de Sudokus, veremos que encuentra las dos soluciones con 49 Naked singles y 1 vuelta atrás. Si buscamos pistas hasta llegar al vuelta atrás observaremos el estado del tablero tal como se observa en la Figura.

Vemos que antes de aplicar el backtrack hay sólo cuatro celdas que llenar, todas con los mismos diponibles '69'. Si en una ponemos '6', en la otra en la misma fila hemos de poner '9'. Y sus opuestos en la otra fila. Esto conduce a esas dos soluciones para el Sudoku.

Por lo tanto para ese tablero no aplica el concepto de unicidad, pues tiene dos soluciones. Pero cuando aplicamos las técnicas de resolución partimos de la base de que el Sudoku se planteó en un tablero inicial para que tuviera solución única. El rectángulo de NO unicidad formado por las cuatro celdas sin llenar que se observa en la Figura no puede darse nunca en un verdadero Sudoku. Ese rectángulo que debemos evitar se suele denominar patrón mortal o deadly pattern en la terminología en inglés. En lo que sigue veremos como aprovechar estos conceptos para encontrar y borrar números disponibles, para lo cual hemos de evitar que aparezca un rectángulo de no unicidad.

En este y siguientes temas veremos estas técnicas de unicidad:

• Rectángulo único (I)
• Rectángulo único (II)
• Rectángulo único (III)
• Rectángulo único (IV)
• Rectángulo único (V)
• Rectángulo oculto (I)
• Rectángulo oculto (II)
• Rectángulo evitable (I)
• Rectángulo evitable (II)
• BUG+1

Rectángulo único I (Unique rectangle I)

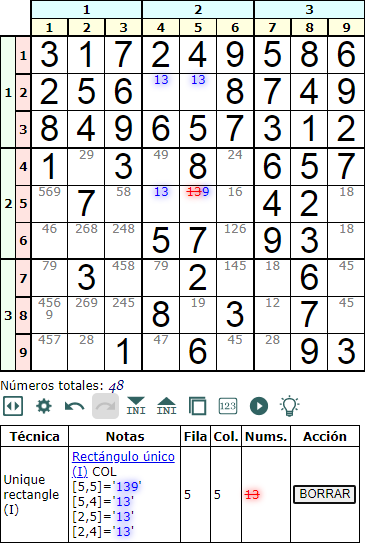
En la Figura vemos en ejecución la técnica de resolución o profundizado rectángulo único tipo I en columna (unique rectangle type I column). La disposición de las cuatro celdas [2,4]='13', [2,5]='13', [5,4]='13' y [5,5]='139' conforman ese rectángulo.

Para evitar que aparezca un rectángulo de no unicidad no podemos permitir que la celda [5,5] resulte con los disponibles '13', igual que las otras tres. Para conseguirlo borramos los disponibles '13' en esa celda. Hay que pensar que al generar ese Sudoku con solución única, en esa celda [5,5]='139' solo cabía el '9', pues '1' o '3' forman parte del rectángulo de no unicidad.

Para este rectángulo único en columnas, las dos esquinas superiores estarán ubicada en una fila dentro de una misma caja. Mientras que las dos esquinas inferiores se ubican en otra banda en las mismas columnas. Recordar que una banda es una fila de cajas y una pila es una columna de cajas. Para este tipo I se trata de encontrar un rectángulo con tres esquinas con dos disponibles 'ab' y una cuarta esquina con esos dos disponibles mas un tercero distinto 'abc'.

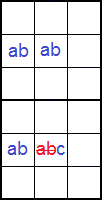
El esquema de la Figura refleja el rectángulo tipo I en columna. Se trata de dos cajas en la misma pila, donde dos celdas se ubican en una fila de la caja superior y otras dos en la caja inferior, en las mimas columnas, formando así un rectángulo. Tres esquinas tienen los mismos disponibles 'ab' y una esquina tiene tres disponibles 'abc', eliminándose 'ab' de esta celda.

La otra estructura que podemos encontrar es el rectángulo único tipo I fila (unique rectangle type I row). Un ejemplo se observa en la Figura. El rectángulo aparece en la última banda, con dos esquinas en la caja central y las otras dos en la última caja.

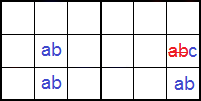
En la Figura vemos el esquema de este rectángulo tipo I en fila. Dos esquinas del rectángulo se ubican en una caja y otras dos en otra caja en la misma banda. Tres esquinas tienen los mismos disponibles 'ab'. La cuarta esquina tiene 'abc' y se eliminan los disponibles 'ab'.

Unicidad y Sudokus con múltiples soluciones

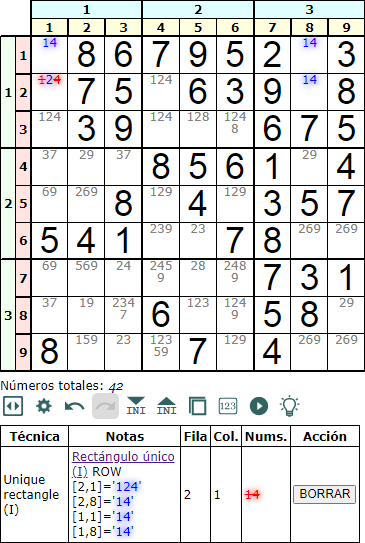
El tablero inicial de la Figura es de un Sudoku con 18 soluciones. Resolviéndolo sólo con vuelta atrás se necesitan 3451 iteraciones para encontrar las 18. Si intentamos resolverlo usando las técnicas de resolución o profundizado, incluyendo las del grupo Uniqueness

Veremos que se genera el error: El tablero con 24 iniciales se resolvió con solución única sin vuelta atrás, pero no tiene solución única: alguna técnica de profundizado no se aplicó correctamente o bien se aplicó alguna técnica de unicidad a un Sudoku con más de una solución. Si quiere ver todas las soluciones desactive el grupo Uniqueness (o las defectuosas) en la configuración. Como dice el mensaje, para ver todas las soluciones hay que desactivar el grupo Uniqueness.

Esto quiere decir que no podemos aplicar técnicas de unicidad a Sudokus con más de una solución. En el ejemplo podemos ver el primer rectángulo único tipo I en fila que se obtiene con la ejecución de pistas. Si fuera de solución única podríamos aplicar esa técnica. Pero al tener múltiples soluciones no podemos considerar que en la celda [2,1] no puedan caber los disponibles '1' o '4'.