Recursivos en algoritmos del tipo vuelta atrás
El problema de las 8 reinas
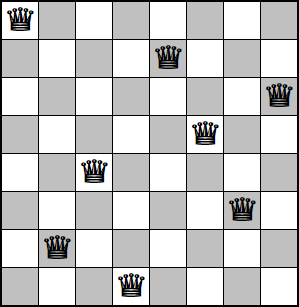
El problema de las 8 reinas se plantea cómo ubicar en un tablero de ajedrez ocho reinas de tal forma que no se amenacen entre ellas. Esto quiere decir que no puede haber más de una en cada fila, columna o diagonal. Hay más de una solución, pero en esta versión del problema solo nos interesara encontrar la primera solución, como la de la Figura.
Este tipo de problemas no puede solucionarse aplicando las técnicas de reducción por substracción o división (divide y vencerás), puesto que no hay una evidencia clara de como reducir el problema a uno de menor tamaño. Esto significa que no queda más remedio que ir probando todas las combinaciones hasta que demos con la primera solución. Hay 64 casillas posibles y 8 piezas, por lo que existen 4.426165368 × 109 combinaciones de 8 elementos a ubicar en 64 casillas.
El número de combinaciones de p elementos elegidos de un conjunto de n elementos es C(n, p) = n! / p!(n-p)! En nuestro problema vemos que el número de reinas es igual que las medidas del tablero, así que tenemos C(n2, n) = (n2)! / n!(n2-n)! Y ya vimos en un tema anterior que un algoritmo con coste factorial se vuelve intratable con tamaños no muy grandes.
Aunque demos con la primera solución antes de recorrer todas las combinaciones, hay que tratar de reducir el número de posibilidades. Y este es el objetivo de los algoritmos recursivos del tipo vuelta atrás o backtracking. Por ejemplo, para conseguir la primera solución de la Figura sólo tenemos que analizar 25944 combinaciones.
Para explicar como funciona un vuelta atrás vamos a usar un tablero más pequeño de 4×4 donde ubicaremos 4 reinas. Haremos el recorrido de las combinaciones siguiendo una estructura de árbol como el siguiente grafo hasta que consigamos la primera solución:
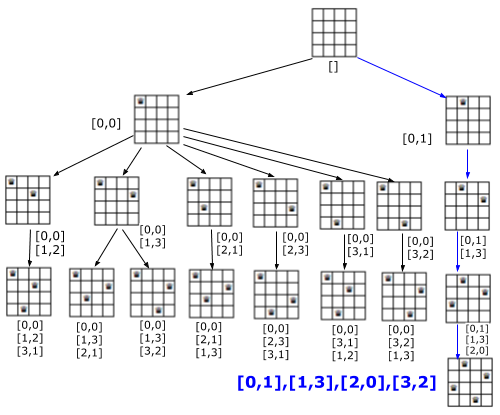
Ese grafo realmente no existe, sino que lo vamos construyendo a medida que generamos cada combinación. Empezamos con un tablero vacío y luego colocamos una primera reina en la posición [0, 0], generándose un nodo y recordando que las posiciones se inician en cero. Seguimos buscando casillas hacia la derecha y hacia abajo del tablero para colocar las siguientes reinas. Vemos que sólo es posible colocarla en la posición [1, 2] pues en las anteriores resulta amenazada por la primera reina. Tenemos ahora el nodo que se representa como un array de dos posiciones de reinas colocadas: [0,0], [1,2]. Seguimos avanzando por la primera rama izquierda del árbol y encontramos una posición no amenazada para la tercera reina generándose el nodo [0,0], [1,2], [3,1]. Al llegar a este punto ya no podemos colocar la cuarta reina sin ser amenazada. Esa rama no tiene éxito y la abandonamos puesto que ya no hay forma de colocar 4 reinas que es la solución buscada.
Abandonar una rama significará que hacemos una vuelta atrás hasta la anterior bifurcación en el nodo [0, 0], desde donde intentaremos ver si tiene solución en una nueva rama. Como se observa en la Figura no hay más soluciones hasta la rama de la derecha, donde la solución está en el nodo [0,1], [1,3], [2,0], [3,2]. Como el problema sólo nos pide la primera solución finalizamos aquí. Si nos pidieran todas las soluciones seguiríamos desplegando el árbol. Se observa que el árbol tiene una profundidad de 4 nodos desde el nodo raíz, pues sólo hay 4 reinas que colocar. Y tiene una anchura también de 4, que se miden en el primer nivel después del raíz, ancho que es el número de casillas de la fila del tablero.
Para implementar un vuelta atrás es preferible usar un código con cierta estructura que se repetirá en todos los problemas de este tipo. Es aconsejable implementar las funciones auxiliares aparte, pues así tendremos un código más claro y entendible:
function reinas(n){
let tableros = [[]];
let nodoVacio = crear(n);
(function generarTablero(nodo){
if (esSolucion(nodo)){
guardar(nodo, tableros);
return true;
} else {
for (let i=0; i<nodo.n; i++){
for (let j=0; j<nodo.n; j++){
if (acotar(nodo, i, j)){
probar(nodo, i, j);
if (generarTablero(nodo)) return true;
deshacer(nodo);
}
}
}
return false;
}
})(nodoVacio);
return tableros;
}La función reinas(n), que no es un recursivo, nos sirve para iniciar la ejecución y devolvernos la solución. En el problema la solución es un conjunto de tableros donde iremos guardando todas las soluciones encontradas. Particularmente para este ejemplo sólo nos piden la primera solución. Declaramos entonces la variable tableros global al recursivo interior generarTablero(nodo). No es recomendable usar variables globales, pero en este caso si la limitamos a la variable que guarda las soluciones, podemos evitarnos arrastrarla en la ejecución del recursivo. Además es global sólo con respecto a la ejecución del recursivo, por lo que podremos controlar sus efectos.
Necesitaremos una estructura de un único nodo para ir recorriendo el árbol implícito. La función crear(n) nos devuelve un nodo vacío que contendrá un Array con las posiciones tal como vimos en la Figura. Guardamos aquí también el valor n que son las dimensiones del tablero y del número de reinas pues lo necesitaremos en la ejecución. Este valor n viene a ser una variable estática que no se va a modificar, siendo preferible ponerla aquí en lugar de arrastrarlas en argumentos de las sucesivas llamadas del recursivo.
function crear(n){
return {reinas: [], n};
}Hacemos que la función recursiva generarTablero(nodo) se auto-ejecute, pasándole como argumento el nodo vacío. Dentro del recursivo encontramos las siguientes funciones accesorias, todas ellas muy simples. Podría pensarse en poner esos códigos directamente dentro de la función principal, evitándonos un exceso de llamadas a funciones. Quizás en una implementación final para producción podría hacerse, pero mientras desarrollamos el problema conviene separarlas por claridad.
Dentro del recursivo analizamos si el nodo es una solución, lo que sucederá si tenemos todas las reinas colocadas, devolviendo un valor booleano verdadero y guardando esa solución en la posición cero de la variable tableros.
function esSolucion(nodo){
return nodo.reinas.length === nodo.n;
}
function guardar(nodo, tableros) {
tableros[0] = [...nodo.reinas];
}Si el nodo no es una solución pasamos a generar nuevos nodos iterando en el rango 0..n × 0..n que son todas las casillas del tablero. Hacemos una poda de la rama mediante la funcion acotar(nodo, i,j) para no tomar aquellas casillas que resulten amenazadas por otras reinas ya colocadas. Si una casilla es posible pasamos a probar ese nodo con probar(nodo, i,j) tras lo cual realizamos una nueva llamada al recursivo. Tras volver vemos si ha sido una solución en cuyo caso devolvemos verdadero y no seguimos generando más nodos. Si fuera falso deshacemos la prueba del nodo para generar otro.
function acotar(nodo, i, j){
return nodo.reinas.every(v => v[0]!==i && v[1]!==j &&
Math.abs(v[0]-i)!==Math.abs(v[1]-j));
}
function probar(nodo, i, j){
nodo.reinas.push([i,j]);
}
function deshacer(nodo){
nodo.reinas.pop();
}Ejemplo: El problema de las 8 reinas
El problema de la mochila

En el problema de la mochila nos dan una que puede cargar un peso máximo de 8 kg. En ella podemos llevarnos cuatro clases de objetos: violines, trompetas, guitarras y saxofones, cada uno con un peso y un valor. Podemos disponer de una cantidad ilimitada de cada uno de ellos. El problema es llenar la mochila con objetos sin pasarnos del peso máximo y con el objetivo de maximizar el valor total.
En este ejemplo hay varias posibilidades para combinar un peso total igual o menor de 8 kg. Por ejemplo, dos violines (20 €), una trompeta y una guitarra (70 €), un violín y dos saxofones (50 €), cuatro saxofones (80 €), etc. La combinación de dos trompetas y un saxofón (100 €) es una solución del problema. Con cuatro objetos esa solución puede empezar a vislumbrarse tras pasar un rato pensando en las combinaciones de pesos y valores. Pero si tuvieramos más objetos ya no sería tan sencillo.
Para automatizar la búsqueda de la combinación óptima hemos de iterar por todas las combinaciones posibles. En este tipo de problemas hay un grafo implícito, grafo que iremos creando a medida que lo recorremos:
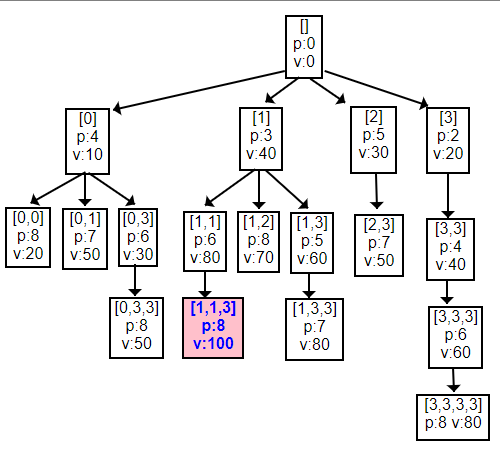
Empezamos con el nodo raíz, una mochila vacía [], p:0, v:0. Cada nodo se representa con tres valores: un Array con los índices de los objetos que metemos en la mochila (teniendo en cuenta que se inician en cero), el peso y el valor de la mochila.
Los objetos ["🎻", "🎺", "🎸", "🎷"] vienen definidos por sus pesos [4, 3, 5, 2] y por sus valores [10, 40, 30, 20]. El peso máximo que podemos meter en la mochila son 8 kg. Tomamos el primer objeto y tenemos una mochila [0], p:4, v:10, teniendo capacidad para seguir metiendo objetos. Volvemos a meter otro primer objeto quedando [0,0], p:8, v:20. Esta mochila tiene más valor que la anterior (20 €) y la anotamos como óptima hasta el momento. Hemos llenado la mochila pues ya tiene 8 kg y no podemos seguir metiendo. Esta rama del árbol finaliza aquí: hemos llegado a una hoja final de esa rama. Pero tenemos que seguir buscando todas las combinaciones posibles pues alguna puede tener un valor superior. Esto equivale a decir que hay que recorrer todo el árbol.
El segundo nodo final es [0,1], p:7, v:50 y tiene mejor valor, por lo que anotamos esta mochila y descartamos la anterior. Pasamos al siguiente nodo [0,2] y vemos que su peso 4+5 = 9 supera los 8 kg. Ese nodo no forma parte del árbol. Por último en esta rama pasamos a [0,3], p:6, v:30 y aún nos caben 2 kg más por lo que tenemos una subrama [0,3,3], p:8, v:50. Este valor de 50 € es igual que el último anotado, pero no lo anotamos porque ya teníamos una mochila con ese valor.
Seguimos este proceso construyendo y recorriendo el árbol. En el diagrama verá que en la segunda rama obviamos [1,0], p:7, v:50 pues es equivalente al de la primera rama [0,1], p:7, v:50. Entonces iteramos siempre desde el índice actual hasta la derecha, pues hacia la izquierda ya fueron contemplados en los índices anteriores.
En esa segunda subrama observará que llegamos al nodo [1,1,3], p:8, v:100 que es la mejor solución. Es única con valor 100 € en este ejemplo.
El código del recursivo sigue el mismo esquema que vimos en el apartado anterior, aunque con una leve diferencia. Antes sólo nos interesaba la primera solución. Pero ahora una solución es aquella que tenga mayor valor que la solución guardada previamente. Esto significa que hay que recorrer todo el árbol.
function mochila(maxPeso, pesos, valores){
let objetos = [[]];
let nodoVacio = crear(maxPeso, pesos, valores);
(function llenarMochila(nodo){
if (esSolucion(nodo, objetos)){
guardar(nodo, objetos);
}
for (let i=nodo.n; i<nodo.pesos.length; i++){
let pesoLibre = acotar(nodo, i);
if (pesoLibre>=0){
probar(nodo, i);
llenarMochila(nodo);
deshacer(nodo, i);
}
}
})(nodoVacio);
return objetos;
}Empezamos creando el nodo vacío que contiene la variable n que evitará generar nodos equivalentes, por ejemplo, el nodo [1, 0] es el mismo nodo que ya habíamos generado previamente [0, 1]. La varible bak nos servirá para deshacer el nodo como veremos luego. En el array objetos tendremos los objetos que tenemos en la mochila hasta el momento. El pesoLibre nos dirá que peso podemos aún meter en la mochila. Disponemos también de las tres variables estáticas inciales que definen el problema y que las colocamos en este objetos para evitar acceder a ellas como variables globales o arrastrarlas como argumentos en las llamadas: maxPeso, pesos y valores.
function crear(maxPeso, pesos, valores){
return {
n: 0,
bak: 0,
objetos: [],
pesoLibre: maxPeso,
maxPeso,
pesos,
valores
}
}Como dijimos, vemos si la mochila que estamos probando tiene mayor valor que la última almacenada, en cuyo caso la sustituimos. Así siempre tendremos en la variable global objetos[0] la mochila con mayor valor:
function esSolucion(nodo, objetos){
let valorMochila = objetos[0].reduce((p,v) => p+nodo.valores[v], 0);
let valor = nodo.objetos.reduce((p,v) => p+nodo.valores[v], 0);
return valor > valorMochila;
}
function guardar(nodo, objetos) {
objetos[0] = [...nodo.objetos];
}La función que poda las ramas es acotar(nodo, i) y simplemente devuelve el peso libre que queda si añadimos un nuevo objeto. Finalizaremos una rama cuando ya no haya más capacidad en la mochila. Pasamos a probar ese nodo guardando el valor de n en la variable bak para cuando deshagamos ese nodo.
function acotar(nodo, i){
return nodo.pesoLibre - nodo.pesos[i];
}
function probar(nodo, i){
nodo.pesoLibre -= nodo.pesos[i];
nodo.bak = nodo.n;
nodo.n = i;
nodo.objetos.push(i);
}
function deshacer(nodo, i){
nodo.pesoLibre += nodo.pesos[i];
nodo.n = nodo.bak;
nodo.objetos.pop();
}Ejemplo: El problema de la mochila
mochila(maxPeso, pesos, valores): En el ejemplo de este apartado y en el del anterior tenemos la posibilidad de trazar el recorrido del árbol. Para ello modificamos el código con lo siguiente:
function llenarMochila(nodo, nivel=-1){
nivel = trazar(nodo, nivel);
...
llenarMochila(nodo, nivel);
...
}La función trazar(nodo, nivel) guarda una cadena de texto con los datos del nodo. El nivel viene a ser el nivel de profundidad del nodo y lo pasamos en el argumento del recursivo.
function trazar(nodo, nivel){
nivel++;
numNodos++;
let peso = nodo.objetos.reduce((p,v) => p+nodo.pesos[v], 0);
let valor = nodo.objetos.reduce((p,v) => p+nodo.valores[v], 0);
traza.push("nivel:" + nivel + " nodo:[" +
[...nodo.objetos] + "] peso:" + peso + " valor:" + valor);
return nivel;
}El problema del cuadrado mágico
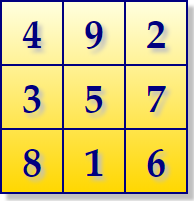
El problema del cuadrado mágico de dimensión n se plantea cómo colocar n2 números naturales en el rango 1..n2 en un tablero con n×n casillas, de tal forma que la suma de las filas, columnas y diagonales resulte siempre el valor n(n2+1)/2. En la Figura puede ver un cuadrado mágico de 3×3 con números 1..9 sumando 15.
Vamos a resolver este problema devolviendo bien la primera solución o todas las soluciones. Para ello pasaremos un segundo argumento todos en la función de inicio cuadradoMagico(). Ahora la solución está en la variable global cuadrados, un array con una solución o bien con todas las soluciones si es que pasamos todos = true. El código a implementar es el siguiente:
function cuadradoMagico(n, todos=false){
let cuadrados = [];
let nodoVacio = crear(n);
(function generarCuadrado(nodo){
let ok = esSolucion(nodo, cuadrados);
if (ok) guardar(nodo, cuadrados);
if (!ok || todos) {
for (let i=0; i<n; i++) {
for (let j=0; j<n; j++) {
if (nodo.cuadrado[i][j]===0) {
let numero = acotar(nodo, i, j)
if (numero>0){
probar(nodo, i, j, numero);
ok = generarCuadrado(nodo);
if (ok && !todos) return true;
deshacer(nodo, i, j, numero);
}
}
}
}
}
return ok;
})(nodoVacio);
return cuadrados;
}El nodo vacío que necesitaremos es ahora más complejo. El cuadrado será una matriz de n×n. Para evitar tener que sumar filas, columnas y diagonales en cada llamada, guardamos estas sumas. Necesitaremos saber también cuantos números tenemos colocados en una fila o columna, los números usados y los disponibles. Tendremos disponibles las variables estáticas de la suma n(n2+1)/2 y el valor de n. En cota guardaremos suma-n2 cuya finalidad será acotar ramas.
function crear(n){
let n2 = n**2;
let arr = Array.from({length:n}, () => 0);
let suma = n*(n2+1)/2;
let cota = suma-n2;
let nodoVacio = {
cuadrado: Array.from({length: n}, () => [...arr]),
sumaFilas: [...arr],
sumaColumnas: [...arr],
sumaDiagonales: [0, 0],
numerosFila: [...arr],
numerosColumna: [...arr],
numerosUsados: [],
numerosDisponibles: Array.from({length: n2}, (v,i) => i+1),
cota,
suma,
n
}
return nodoVacio;
}Un nodo es solución si las sumas de las filas, columnas y diagonales suman n(n2+1)/2, valor que tenemos guardado como variable estática en nodo.suma. En ese caso guardamos esa solución.
function esSolucion(nodo){
return nodo.sumaDiagonales.every(v => v===nodo.suma) && nodo.sumaFilas.every(v => v===nodo.suma) && nodo.sumaColumnas.every(v => v===nodo.suma);
}
function guardar(nodo, cuadrados){
cuadrados.push(nodo.cuadrado.map(v => [...v]));
}Veamos ahora la función acotar(nodo, i, j). Antes de probar un nuevo número disponible en la casilla i, j realizamos una suma temporal de filas y columnas. Ese nodo será válido si se cumple todo lo siguiente, recordando que nodo.suma es el valor estático n(n2+1)/2 y nodo.cota es suma-n2.
- Las sumas temporales de filas y columnas no superan
nodo.suma - Si estamos probando el último número disponible, esas sumas temporales debe ser exactamente
nodo.suma - Si estamos probando el antepenúltimo número disponible, es decir, sólo quedan dos por poner contando el que estamos probando, las sumas temporales no puede ser menor que
nodo.cotani mayor quenodo.suma-1.
Para entender la tercera validación veamos un ejemplo de un 3×3 donde las sumas deben dar 15 y la cota es 15-9 = 6. Con el número que estamos probando la suma temporal de los dos primeros números de una fila no puede sumar menos de 6 ni mayor de 14 pues no habría un número 1..9 que poner en la última casilla de tal forma que los tres sumen 15. Si por ejemplo la suma temporal es 5 como máximo pondríamos un 9 en la última y tendríamos 5+9=14 no llegando a 15. Y si la suma temporal fuera 15 o mayor ya nos habríamos pasado puesto que aún falta un número que poner.
function acotar(nodo, i, j){
let numero = nodo.numerosDisponibles[nodo.numerosDisponibles.length-1];
let sumFilTemp = nodo.sumaFilas[i]+numero;
let sumColTemp = nodo.sumaColumnas[j]+numero;
let valido = sumFilTemp<=nodo.suma && sumColTemp<=nodo.suma &&
!(nodo.numerosFila[i]===nodo.n-1 && sumFilTemp!==nodo.suma) &&
!(nodo.numerosColumna[j]===nodo.n-1 && sumColTemp!==nodo.suma) &&
!(nodo.numerosFila[i]===nodo.n-2 && (sumFilTemp<nodo.cota || sumFilTemp>nodo.suma-1)) &&
!(nodo.numerosColumna[j]===nodo.n-2 && (sumColTemp<nodo.cota || sumColTemp>nodo.suma-1));
return valido ? numero : 0;
}La acotación válida nos devolverá el número a utilizar o un cero en otro caso. Si es válido pasamos a probar un nuevo nodo, ubicando ese número en el tablero. Sumamos fila, columna y diagonales. Agregamos un número más a los que tenemos en la fila y columna y quitamos ese número de los disponibles y lo pasamos a los usados. Si tras la llamada vemos que no es solución, deshacemos ese nodo.
function probar(nodo, i, j, numero){
nodo.cuadrado[i][j] = numero;
nodo.sumaFilas[i] += numero;
nodo.sumaColumnas[j] += numero;
if (i===j) nodo.sumaDiagonales[0] += numero;
if (i===nodo.n-j-1) nodo.sumaDiagonales[1] += numero;
nodo.numerosFila[i]++;
nodo.numerosColumna[j]++;
nodo.numerosUsados.push(nodo.numerosDisponibles.pop());
}
function deshacer(nodo, i, j, numero) {
nodo.cuadrado[i][j] = 0;
nodo.numerosFila[i]--;
nodo.numerosColumna[j]--;
nodo.sumaFilas[i] -= numero;
nodo.sumaColumnas[j] -= numero;
if (i===j) nodo.sumaDiagonales[0] -= numero;
if (i===nodo.n-j-1) nodo.sumaDiagonales[1] -= numero;
nodo.numerosDisponibles.push(nodo.numerosUsados.pop());
}Es importante observar que estas funciones accesorias son más complejas que las que vimos en los ejemplos anteriores. Por eso es recomendable mantenerlas separadas para analizar y mantener el código de la función recursiva con más claridad.
Ejemplo: Cuadrado mágico
cuadradoMagico(n):Si no usamos un vuelta atrás y buscamos todas las posibilidades deduciremos que pueden ser muchas. En un cuadrado de n×n tendríamos n2 números a ubicar en tantas posiciones como permutaciones (n2)! Para 3×3 tenemos todas las permutaciones de los números 1, 2, 3, ..., 9 que serán 9! = 362880. El vuelta atrás que hemos implementado sólo necesita analizar 142 nodos para la primera solución y 729 nodos para encontrar todas las soluciones.
Si pasamos a un cuadrado de 4×4 habrán 16! = 2.092279×1013 permutaciones. Nuestro ejemplo encuentra la primera solución analizando 39159 nodos. Pero con diez millones de nodos analizados no puede cubrir todas las soluciones. Si pasamos a uno de 5×5 habrán 25! = 1.551121×1025 permutaciones. Ni siquiera analizando los diez millones de primeros nodos conseguimos obtener la primera solución.
De nuevo el problema de un coste factorial. Con tamaños mayores de cuatro el problema se vuelve intratable. En el ejemplo damos la posibilidad de inciar el recursivo con un nodo de 5×5 parcialmente rellenado, tomando sólo las dos primeras filas y poniendo un cero en las tres últimas. Este cuadrado mágico lo he obtenido de la página culturacientifica.com, que comenta cosas interesantes sobre el tema, aunque no desde la perspectiva de los algoritmos recursivos.
Un detalle interesante es que si C(n) es un el número de soluciones de un cuadrado mágico de orden n, tenemos que C(1)=1, C(2)=0, C(3)=1, C(4)=880 y C(5)=275305224 soluciones. Para C(6) se ha estimado que hay aproximadamente 1.7745×1019 soluciones (ver también Wikipedia y OEIS).
El cuadrado de orden 3 tiene una solución y nuestro ejemplo nos da 8. Esto es porque son rotaciones y simetrías unas de otras. A un cuadrado de orden 3 podemos practicarle cuatro rotaciones de 90° y cuatro simetrías (dos en cada eje) de tal forma que se conservan las sumas de filas, columnas y diagonales. En el orden 4 hay 880 soluciones, que con rotaciones y simetrías serán muchísimas más soluciones. Es de notar que no hay soluciones de orden 2, tal como también resulta en nuestro ejemplo. De orden 1 hay una solución evidente y sus rotaciones y simetrías producen el mismo único resultado.