Aplicación para gestionar Sudokus

Un Sudoku es un juego consistente en un tablero de 9×9 celdas con las restricciones de colocar un número del conjunto {1,2,3,4,5,6,7,8,9} en cada celda debiendo aparecer sólo uno de ellos en cada fila, columna y caja. Una caja es cada uno de los rectángulos de 3×3 celdas. Las cajas se agrupan en filas denominadas bandas y columnas denominadas pilas. El objetivo del juego es rellenar todas las celdas respetando esas restricciones.

Un tablero es un juego con unos números iniciales que reducen el número de combinaciones posibles para obtener un resultado, que puede ser de solución única o de múltiples soluciones. Se entiende que un verdadero Sudoku es aquel que produce una solución única. No todas las combinaciones de números en celdas dan como resultado un Sudoku con solución única, pues la mayor parte producen múltiples soluciones. Incluso muchas combinaciones ni siquiera permiten completarlo.

Como se observa en la Figura, la aplicación nos permite generar un tablero con números iniciales partiendo de una muestra almacenada. O bien generar aleatoriamente un nuevo Sudoku. Todas las muestras almacenadas fueron obtenidas con ese generador aleatorio.

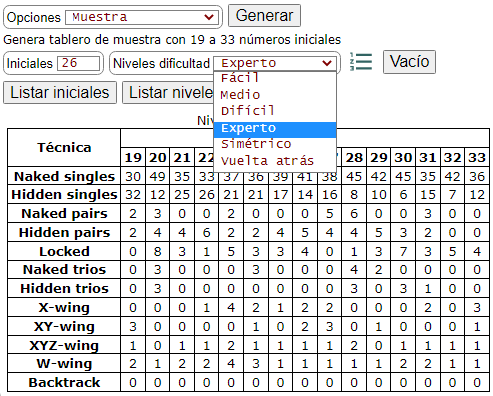
En la Figura puede observar la generación de tableros de muestra. Por ahora se establecen los niveles de dificultad fácil, medio, difícil y experto. Por cada uno de ellos y también por el el número de iniciales desde 19 a 33 hay un tablero de muestra. También hay muestras para tableros simétricos y con vuelta atrás. Es posible ejecutar todas las muestras y verter sus resultados en una tabla, como la que se observa en la Figura. Podemos listar por iniciales o bien por niveles de dificultad.

También podemos aplicar una transformación a un tablero de tal forma que el nuevo tablero es otra representación equivalente del mismo Sudoku. Las transformaciones se basan en reetiquetar, permutar, transponer, rotar y reflejar. En un apartado siguiente explicaremos algo más sobre esto. Por último la aplicación nos permite importar y exportar un tablero en formato de texto.

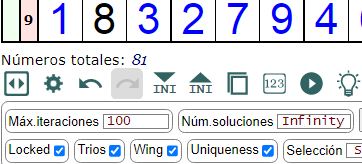
Bajo el tablero encontramos una barra de botones para la ejecución de la resolución del Sudoku, como se observa en la Figura. Los iconos de los botones representan estas acciones:

• Resetear aplicación. Cuando modificamos el ancho de pantalla podemos reajustar el tamaño del tablero para que ocupe el ancho de pantalla.
• Abre el panel de configuración de resolución del Sudoku.
• Deshace una acción
• Rehace una acción
• Guarda el tablero actual en pantalla como tablero inicial.
• Extrae el tablero inicial guardado y lo vuelca en el tablero en pantalla.
• Copia el tablero actual en el portapapeles en formato texto, poniendo un "*" en las celdas vacías, separando las celdas con un espacio y las filas con un salto de línea.
• Muestra u oculta los números disponibles o candidatos.
• Ejecuta la resolución del Sudoku.
• Busca la siguiente pista aplicando una técnica de resolución o profundizado.

El icono de la barra de botones de la aplicación tiene por objeto guardar el tablero actual como tablero inicial. Mientras que el botón extrae el tablero inicial guardado y lo vuelca en el tablero en pantalla. Cuando generamos un tablero mediante el botón "Generar" de la aplicación, el tablero que se vuelca en pantalla se convierte en tablero inicial. Pero si rellenamos a mano el tablero no se modifica el tablero inicial, a menos que pulsemos el botón para guardar nuevamente el tablero como inicial. La técnica de rectángulos evitables usa el tablero inicial para consultar el estado previo.

Esta aplicación permite resolver cualquier sudoku usando el algoritmo de vuelta atrás (backtracking).Esto lo explicaremos en el siguiente tema. También se utilizan algunas de las técnicas de resolución (o profundizado) más conocidas como veremos en un apartado siguiente. Denominamos en la aplicación a la acción de profundizar el hecho de aplicar estas técnicas. El significado de ese nombre se refiere a profundizar en el árbol del vuelta atrás, como veremos en el siguiente tema.

El profundizado: estudiando las técnicas de resolución de Sudokus

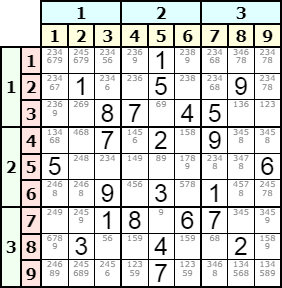
Las técnicas de resolución o profundizado nos permiten resolver un Sudoku sin utilizar el último recurso del vuelta atrás. O bien reducir significativamente el número de iteraciones del vuelta atrás para completarlo. Uno de los motivos principales por los que hice esta aplicación fue estudiar esas técnicas de profundizado e implementarlas en un algoritmo.

El Sudoku de la Figura se puede resolver en apenas 5 ms con solución única usando esas técnicas de profundizado y sin utilizar vuelta atrás. Si sólo usáramos vuelta atrás prescindiendo del profundizado, necesitaríamos fijar el parámetro de máximo de iteraciones superior a 35991, puesto que esas son las que se necesitan para resolverlo con el algoritmo del vuelta atrás.

En cada ejecución se obtiene un resumen como el siguiente (observe el máximo establecido de 36000 iteraciones y el tiempo empleado 296 ms):

RESULTADO
---------
Números iniciales: 24 (color negro)
Límite iteraciones vuelta atrás: 36000
Número máximo de soluciones a devolver: Infinity
Profundizado: false
    Singles: false
    Pairs: false
    Trios: false
    Locked: false
    Wing: false
Selección: Siguiente
Tiempo total: 296 ms
Soluciones encontradas en 36000 iteraciones: 1
Pueden haber más soluciones pues se llegó al máximo de iteraciones.

RESULTADO DE LA PRIMERA SOLUCIÓN:
Tiempo: 296 ms
Iteraciones: 35991
Números en profundiza: 0 (color azul)
Naked singles: 0
Hidden singles: 0
Naked pairs: 0
Hidden pairs: 0
Naked trios: 0
Hidden trios: 0
Locked: 0
X-wing: 0
XY-wing: 0
Números en vuelta atrás: 57 (color rojo)

Estado inicial:
* * * * 1 * * * *
* 1 * * 5 * * 9 *
* * 8 7 * 4 5 * *
* * 7 * 2 * 9 * *
5 * * * * * * * 6
* * 9 * 3 * 1 * *
* * 1 8 * 6 7 * *
* 3 * * 4 * * 2 *
* * * * 7 * * * *

Estado final con 1 soluciones:

Solución 1:
4 7 5 9 1 2 3 6 8
6 1 2 3 5 8 4 9 7
3 9 8 7 6 4 5 1 2
1 6 7 4 2 5 9 8 3
5 4 3 1 8 9 2 7 6
8 2 9 6 3 7 1 4 5
2 5 1 8 9 6 7 3 4
7 3 6 5 4 1 8 2 9
9 8 4 2 7 3 6 5 1

Otro detalle es que usando solo vuelta atrás no podemos asegurar siempre que la solución sea única. El algoritmo tendría que analizar todas las combinaciones posibles para poder determinar que no hay alguna solución más. En ese ejemplo habría que fijar un máximo de iteraciones superior a 87000 para comprobar todas las combinaciones y verificar que no encontró más soluciones.

Sin embargo con profundizado el número de combinaciones posibles para aplicar vuelta atrás son inferiores, incluso sólo una cuando el Sudoku se resueve sólo con profundizado. Por eso es posible determinar que cuando el algoritmo finaliza antes de completar el máximo de iteraciones la solución encontrada es única. En otro caso, si se completa el máximo de iteraciones que hayamos impuesto sin haber completado todas las combinaciones posibles, no podemos asegurar que no hayan más soluciones.

Las técnicas que actualmente están implementadas en la aplicación son las siguientes (iré actualizando esta lista a medida que implemente nuevas técnicas).

Los números disponibles o candidatos de una celda, o pencil marks en la terminología sobre Sudokus en inglés, son aquellos posibles que podrían caber en alguna de las combinaciones del tablero. En la aplicación podrá observar que se presentan como una lista de números en cada celda vacía. Cuando hay un único número disponible entonces es que ese número va necesariamente en esa celda. Es lo que se determina con los únicos solitarios o naked singles.

Si entre todos los números disponibles de una fila, columna o caja se produce una aparición de un número una única vez, entonces ese número también va en esa celda. Esto es lo que se denomina número único oculto o hidden single. Estas dos técnicas son las únicas que van encontrando números para las celdas. El resto de técnicas reducen el número de disponibles de tal forma que hace que aparezcan únicos solitarios u ocultos. O bien simplifican los disponibles para que aquellos aparezcan en un paso posterior.

* * 1 * 2 5 7 3 *
* 7 * * 9 1 5 8 2
2 5 * * 7 * * 1 *
* 1 * 7 * 8 * * 3
7 8 5 * * * 1 * *
6 * * 1 * * 8 * 7
* * * * 1 * 2 7 5
5 9 4 2 8 7 3 6 1
1 2 7 5 3 6 4 9 8

Para observar un ejemplo tomaremos como tablero inicial el de la Figura copiando ese texto e importándolo en la aplicación. Usando el botón con el icono , nos ofrecerá la siguiente pista con una técnica de resolución a aplicar.

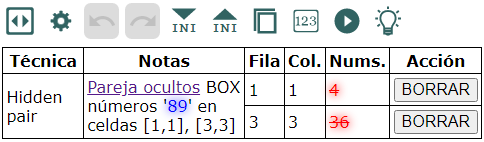
En la Figura se observa que la pista nos descubre una pareja de ocultos (Hidden pair) en una caja que incluye las celdas [1, 1] y [3, 3]. La pareja de números es 89, permitiéndonos borrar el resto de números que le acompañan en esas celdas, es decir, 4 y 36.

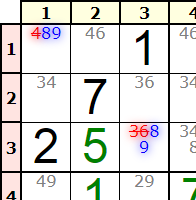
Aunque no es el momento de entrar en más detalles, se observa en la Figura como la aplicacion resalta los números afectados en el tablero. Como la pareja de números 89, es decir, el 8 y el 9, sólo aparecen en dos celdas de la caja, entonces deben ir ahí necesariamente, con lo que el resto de números de esas celdas pueden ser eliminados. Esta acción no descubre un nuevo número para una celda, pero al ir disminuyendo la cantidad de números disponibles tendremos más posibilidad de encontrarlos en pasos posteriores.

Por ahora no voy a explicar en profundidad todas las técnicas de resolución. Hay muchas que ni siquiera he afrontado y, por otro lado, tendría que tratarlas en uno o varios temas aparte. En cualquier caso las pistas de la aplicación ayudarán a empezar a entender las que ya he implementado.

Agregando nuevas técnicas a la aplicación

En relación con las muestras de la aplicación así como los ejemplos en texto e imágenes sobre tableros resueltos de estos temas, hay que entender que se han generado todos con la aplicación. Además hay que observar que se obtienen con la configuración actual de esta aplicación. Inicialmente funcionaban con las técnicas de profundizado que en ese momento estaban implementadas: naked and hidden singles, naked and hidden pairs, naked and hidden trios, locked, X Wing y XY Wing. Si en el futuro decido agregar nuevas técnicas, el resultado no tiene porque ser igual. Por ejemplo, tras posteriormente implementar las técnicas Wing, el siguiente Sudoku se resuelve de la siguiente forma:

Números en profundiza: 55 (color azul)
Naked singles: 31
Hidden singles: 24
Naked pairs: 1
Hidden pairs: 2
Naked trios: 0
Hidden trios: 3
Locked: 4
X-wing: 1
XY-wing: 1
Números en vuelta atrás: 0 (color rojo)

Estado inicial:
* * 2 * * * * 1 8
* 3 5 * * 8 * * *
* * 8 * * 9 * * *
* * * 5 * * 6 * 9
* * * 7 2 * * * 1
8 6 * * * * * * *
* * * * 9 2 4 * *
* 7 * * * * 1 3 *
2 * * * 7 1 * 8 *

Vease que se usa un X-wing y un XY-wing para conseguir que el Sudoku se resuelva sin vuelta atrás. Pero si desmarcamos la opción de usar Wing tal como se observa en la Figura, se obtiene el siguiente resultado, donde es necesario usar un vuelta atrás para resolverlo dado que no se usa la técnica XY-wing:

Números en profundiza: 54 (color azul)
Naked singles: 30
Hidden singles: 24
Naked pairs: 1
Hidden pairs: 2
Naked trios: 0
Hidden trios: 3
Locked: 4
X-wing: 0
XY-wing: 0
Números en vuelta atrás: 1 (color rojo)

Esto quiere decir que si se agregan nuevas técnicas a la aplicación entonces las muestras y ejemplos darán otros resultados. Por un lado los que ahora usan vuelta atrás puede que luego no lo necesiten. Y por otro lado las técnicas necesarias para resolverlo no tienen porque ser las mismas.

Transformaciones de un Sudoku

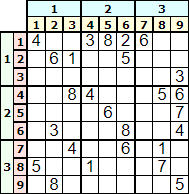
Una solución de un tablero se origina por una combinación de números en unas celdas determinadas. Sin embargo una serie de transformaciones sobre el tablero no modifican esa solución. En la aplicación puede observar que podemos ejecutar las transformaciones reetiquetar, permutar, transponer, rotar y reflejar. Se pueden aplicar una o mas transformaciones sucesivamente resultando siempre la misma solución equivalente. Veamos un ejemplo con la rotación partiendo del tablero inicial de la Figura.

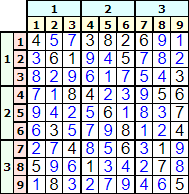
Ese tablero produce la solución de la Figura.

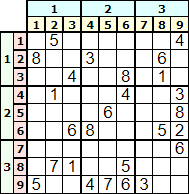
Antes de resolverlo aplicamos una rotación de 90° resultando lo que se observa en la Figura. Vea por ejemplo que los números iniciales de la primera fila 4,"","",3,8,2,6,"","" ahora aparecen en la novena columna.

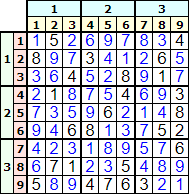
Si resolvemos este tablero rotado observamos en la Figura que la solución es la misma que vimos antes pero rotada 90°. La última columna tiene por números 4,5,7,3,8,2,6,9,1, los mismos de la primera fila en la solución sin rotar.

El reetiquetado se basa en intercambiar los dígitos {1,2,3,4,5,6,7,8,9}. Por ejemplo con la fórmula 10-n. Así obtenemos el nuevo conjunto {9,8,7,6,5,4,3,2,1}. Se obtiene la misma solución sólo que con los nuevos números. De hecho el uso de números en un Sudoku no tiene especial relevancia. Podrían usarse cualesquiera otros símbolos, como letras.

Con las permutaciones intercambiamos bandas o pilas. Y también filas en cada banda o columnas en cada pila. Estas permutaciones no modifican la solución, sigue siendo la misma pero con una permutación en la posición de estos elementos. La transposición intercambia filas por columnas. Por último la reflexión se realiza sobre los ejes intermedios horizontal, vertical y las dos diagonales.

Generando un nuevo Sudoku

El Sudoku es un reto para los que nos gusta programar. Programar no es otra cosa que resolver problemas. Y el Sudoku aporta varios. Uno es implementar un algoritmo para resolver el Sudoku. Esto es en principio fácil. Lo difícil es idear un algoritmo eficiente para generar nuevos tableros Sudoku. Cuando decimos generar un nuevo Sudoku nos referimos a un verdadero Sudoku con solución única.

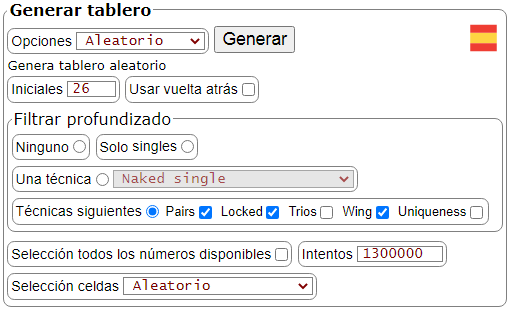
En la aplicación implemento la generación aleatoria de Sudokus, tal como se observa en la Figura. Establecemos los números iniciales. En cualquier caso siempre se usará el profundizado, es decir, siempre buscará solitarios u ocultos (singles). Es posible filtrar el profundizado obligando a que sólo se resuelva con singles. O bien imponer que contenga al menos una de las técnicas de resolución seleccionada pairs, trios, locked, wing, uniqueness y otros nuevos grupos que pueda introducir en el futuro.

Esto no quiere decir que puedan darse otras técnicas, pero las seleccionadas han de ser usadas. Por ejemplo, hemos generado el siguiente tablero sin vuelta atrás y usando las opciones de que se resuelva con al menos una pareja (pairs) y un bloqueado (locked), como se observa en la Figura. El resultado es un tablero que además de varias de esa técnicas usa tres X-wing.

Números en profundiza: 55 (color azul)
Naked singles: 35
Hidden singles: 20
Naked pairs: 0
Hidden pairs: 3
Naked trios: 0
Hidden trios: 0
Locked: 4
X-wing: 3
XY-wing: 0
Números en vuelta atrás: 0 (color rojo)

Estado inicial:
* * * 1 * * 5 * *
* * 3 9 * * 6 7 *
* * 8 6 * * 1 * *
2 * * * 9 * * * 6
6 * * * 7 5 * * *
* * * * * * * 3 4
1 4 * * * * * 6 2
* * * 7 * 6 * * *
* 5 6 * * * 8 * *

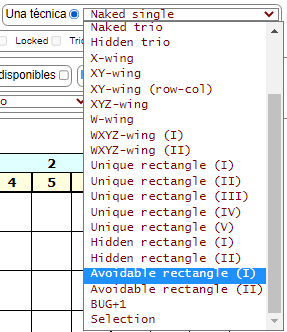
También es posible filtrar por una técnica, como se observa en la Figura. Esto quiere decir que se genera una tablero que al menos contenga esa técnica.

Al final de la lista desplegable de técnicas se observa la entrada "Selection". En caso de usar esa entrada se abrirá un panel donde podemos seleccionar varias técnicas. Y seleccionar en algunos casos también sub-tipos de una técnica. Por ejemplo, la técnica Hidden rectangle (II) tiene los subtipos "abc,ab;abc,ab" y "abc,abc;ab,ab", pudiéndose seleccionar uno de estos subtipos para el tablero generado.

Podemos también forzar a que encuentre un Sudoku que se resuelva con vuelta atrás. En este caso se usa la selección de casilla "siguiente". Debe tenerse en cuenta que al resolver en la aplicación se ha de usar también esta selección para que coincidan los números encontrados en el profundizado.

Si N son los números iniciales establecidos, el proceso selecciona N celdas aleatoriamente desde un tablero vacío y en cada celda elige un número entre los disponibles. A no ser que marquemos la opción que prueba todos los números disponibles en cada celda seleccionada. La selección de celdas también se puede condicionar para producir tableros simétricos. Se establece un máximo de intentos, aunque el proceso puede detenerse en cualquier momento.

El tramo entre 23 y 33 números iniciales genera Sudokus en poco tiempo. Por fuera de esos límites los tiempos se alargan. Con 20 iniciales es costoso conseguirlo, aunque se llegan a obtener. Pero con 19 sólo he podido generar tres Sudokus. Por debajo me ha resultado imposible generar alguno.