Sudoku: Técnicas X-Wing y XY-Wing
Ala X (X-wing)
El grupo de técnicas de profundizado Wing comprende muchas de ellas. En alguna documentación sobre esto las separa en dos grupos: Fish y el propio Wing, estableciendo que X-wing pertenezca a Fish y XY-wing a Wing. Sin embargo las agruparé todas en Wing. Más abajo comentaré algo más sobre esto. La siguiente lista son las técnicas que he implementado:
| Técnica | Vínculo |
|---|---|
| X-wing | Ala X |
| XY-wing | Ala XY |
| XY-wing (row-col) | Ala XY fila-columna |
| XYZ-wing | Ala XYZ |
| W-wing | Ala W |
| WXYZ-wing (I) | Ala WXYZ (I) |
| WXYZ-wing (II) | Ala WXYZ (II) |
En este tema se presentan X-wing y XY-wing que se traduce como Ala X y Ala XY.
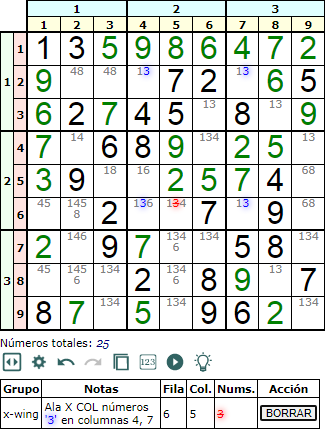
En la Figura puede ver un Ala X (X-wing) en columnas cuarta y séptima. Se observa que el disponible (o pencil mark) '3' sombreado en azul sólo aparece en esas columnas en cuatro celdas que forman un rectángulo: [2, 4], [2, 7], [6, 4] y [6, 7]. Si eso se cumple podemos eliminar los '3' en el resto de celdas de las filas segunda y sexta. En el ejemplo sólo hay una aparición de un '3' en la celda [6, 5] a eliminar.
El principio del rectángulo se basa en que el '3' sólo puede ir ubicado en posiciones opuestas en diagonal. Si va en el celda [2, 4] no podrá ir en la [6, 4] por ser único en la columna. Y si va en la [2, 4] cualquier aparición en la fila segunda no será posible, por lo que no es posible en la celda [2, 7]. Y como es único en la columna séptima debe ir en la [6, 7], ubicándose en posiciones opuestas en diagonal, con lo que también se eliminan las apariciones en la sexta fila. De igual forma se razona tomando cualquiera de las otras esquinas del rectángulo.
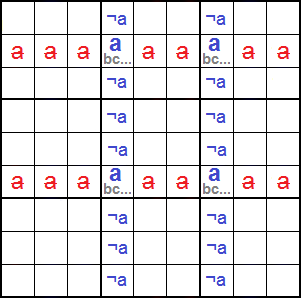
El esquema de la Figura puede explicar mejor la disposición de un X-wing en columna. Encontramos 4 celdas con los disponibles 'abc...', donde 'a' es el número que conforma el X-Wing, siendo 'bc...' cero o más disponibles distintos de 'a' que pudieran haber en esas celdas. Al ser una disposición en columna, encontramos los 'abc...' en las correspondientes esquinas de un rectángulo, disponiéndose dos esquinas horizontales en dos bandas distintas (una banda es una fila de cajas). En el ejemplo los encontramos en las dos primeras bandas. En cuanto a las dos columnas, pueden estar en la misma o distinta pila (una pila es una columna de cajas).
Con '¬a' indicamos que esa celda no tiene 'a' como disponible. Vea que a excepción de las esquinas del rectángulo, 'a' no está entre los disponibles de las dos columnas afectadas. En ese caso podemos eliminar 'a' en los disponibles de las filas afectadas (las que se señalan en rojo y tachado).
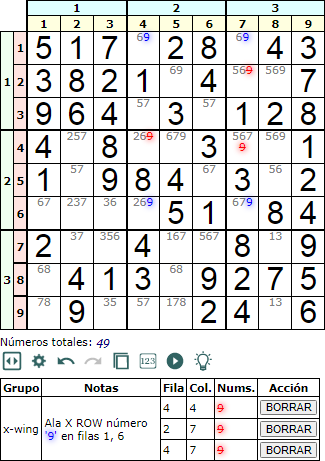
En la Figura puede ver un X-wing en filas primera y sexta, en las posiciones del rectángulo que forman las celdas [1, 4], [1, 7], [6, 4] y [6, 7]. En este caso es un disponible '9' único en esas filas. Por lo tanto podemos eliminar los diponibles '9' en otras celdas de las columnas cuarta y séptima, encontrándonos con '9' a eliminar en las celdas [2, 7], [4, 4] y [4, 7].
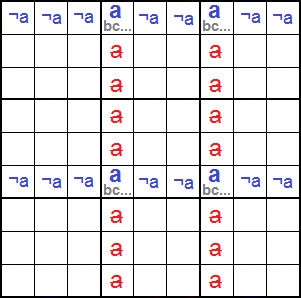
El esquema de la Figura refleja el ejemplo del X-wing en Fila. Vemos que ahora dos esquinas verticales del rectángulo han de disponerse en dos pilas distintas. Pueden estar en la misma o distinta banda. Con '¬a' indicamos que 'a' no se encuentra en esas celdas de las filas a excepción de las esquinas 'abc...'. Con esa disposición podemos eliminar 'a' en las columnas afectadas (señaladas en color rojo).
Al inicio de este tema comenté que X-wing debería pertenecer al grupo Fish. Tal como veremos en ese grupo de temas, estructuralmente se asimila a otras técnicas de ese grupo Fish como Swordfish o Jellyfish. Encontraremos en esos temas las técnicas Finned X-wing y Sashimi X-wing estructuradas a partir del esquema X-wing expuesto.
Ala XY subtipo cajas (XY-wing subtype boxs)

Esta técnica Ala XY (XY-wing) involucra tres parejas de disponibles en tres celdas, dos cajas y dos filas o columnas. En la Figura podemos ver un Ala XY en filas. Ocupa las dos cajas inferiores de la izquierda. Las parejas son de la forma XY = '35', XP = '57' e YP = '37' donde P = '7' es el pivote (pivot) y los X = '5' e Y = '3' son las tenazas o pinzas (pincers). En estas condiciones se puede eliminar el pivote '7' del grupo de tres celdas [7, 4] a [7, 6] así como del grupo [9, 1] a [9, 3].
Esta técnica afecta a dos cajas en la misma banda o pila, no necesariamente contiguas. Recuerde que una banda es una fila de tres cajas y una pila es una columna de tres cajas. Por eso hemos titulado este apartado como Ala XY subtipo cajas, pues hay otro subtipo fila-columna que veremos en un siguiente apartado.
Se razona como sigue. Tomando la pareja XY = '35' en la celda [9, 3] y consideramos que ahí va el '3', entonces en la celda [7, 2] eliminaríamos el '3' e iría un '7', con lo que en el grupo [7, 4] a [7, 6] no puede ir un '7' al estar en la misma fila. Y tampoco en el grupo [9, 1] a [9, 3] por estar en la misma caja.
Si por el contrario en la celda [9, 3] ponemos un '5' entonces en la celda [9, 4] eliminaríamos el '5' y va un '7', con lo que en el grupo [7, 4] a [7, 6] no puede ir un '7' al estar en la misma caja y tampoco en el grupo [9, 1] a [9, 3] por estar en la misma fila.
Nota: En muchas referencias en la web aparece la técnica XY-wing. Pero en algunas (muy pocas) no se menciona esa sino otra denominada Y-wing. Analizándolas veo que se refieren a la misma técnica.
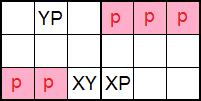
No es fácil detectar esta técnica. En la Figura vemos un esquema del anterior Ala XY en fila. Se observa que involucra dos cajas contiguas en la misma banda. Vemos que hay una caja con XY e YP. Deben estar en dos filas cualesquiera de esa caja, pero no en la misma columna puesto que comparten Y en la caja. En la otra caja tenemos XP en alguna de las tres celdas de la misma fila que XY. Las celdas sombreadas con una "p" minúscula son disponibles que contengan el número pivote.
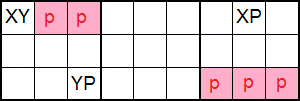
El esquema de la Figura también es de un Ala XY en fila. Las cajas en la misma banda no son contiguas en este caso. Las parejas XY y XP aparecen ahora en la primera fila mientras que YP aparece en la última. XY e YP podrían estar también en filas contiguas, aunque en estos dos ejemplos no es así. Lo que es importante es que XY e YP no estén en la misma fila y columna y que XY y XP estén en la misma fila.
El razonamiento sobre el esquema es que si en XY va X entonces en XP va P y por tanto se eliminan las "p" de la misma fila y caja de XP. Y si en XY va Y entonces en YP va P y por tanto también se eliminan las "p" de la misma fila y caja de YP.

El ejemplo de la Figura refleja el segundo esquema anterior. En este caso XY = '35', XP = '56' e YP = '36'. El pivote es '6' que se elimina en la celda [9, 9]. Si en '35' va el '3' entonces en '36' va el '6' y se elimina en [9, 9]. En cambio si en '35' va el '5' entonces en '56' va el '6' y también se elimina en [9, 9].
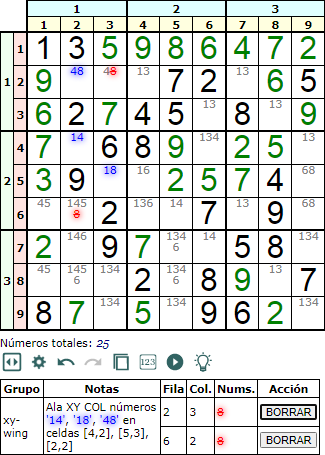
También podemos encontrar Ala XY en columnas, como la de la Figura. Tenemos XY = '14', XP = '48' e YP = '18'. El pivote es P = '8'. Si en '14' optamos por el '1' entonces en '18' va un '8', con lo que podemos eliminarlo en la celdas marcadas en rojo. En cambio si en '14' va el '4' entonces en '48' va un '8' eliminándose también los mismos.
Vease que ahora XY y XP aparecen en la misma columna mientras que antes aparecían en la misma fila.
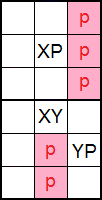
La Figura presenta el esquema de Ala XY en columnas del ejemplo anterior. Tenemos ahora dos cajas contiguas en la misma pila de cajas. Si en XY va X entonces en XP va P y podemos eliminar el número 'p' en las casillas sombreadas. En cambio si en XY va Y entonces en YP va P y también podemos eliminar los mismos 'p'.
Ala XY subtipo fila-columna (XY-wing subtype row-column)
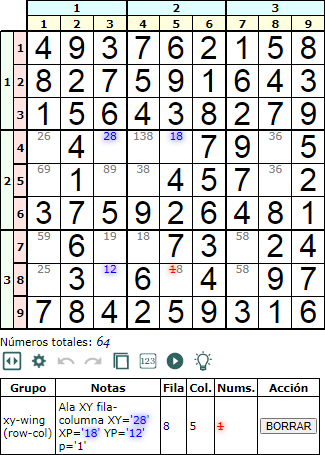
La técnica Ala XY (XY-wing) tiene otro subtipo fila-columna (row-column subtype). En la Figura se observa un ejemplo. Se trata de buscar cuatro celdas que formen un rectángulo con cada esquina ubicada en una caja. En tres esquinas encontramos las parejas XY='28', XP='18' e YP='12. En la esquina opuesta a XY encontramos p='1'.
Razonando como hicimos para el Ala XY subtipo cajas, si en XY='28' optamos por el 2 entonces en YP='12' va un un 1 y por tanto podemos eliminar el 1 en p='1. En cambio si en XY='28' ponemos el 8 entonces en XP='18' va el 1 y también podemos eliminar el 1 en p='1'.En esta técnica sólo podemos eliminar un número.
Las cuatro cajas donde descansan las esquinas del rectángulo son contiguas en este caso. Pero no es necesario que sea así, tal como veremos en siguientes ejemplos.
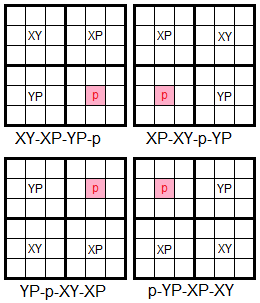
Hay cuatro disposiciones para ubicar las esquinas. En la Figura vemos esos cuatro esquemas ubicando las esquinas en los centros de cuatro cajas contiguas, pero no olvidando que el único requisito es que cada esquina esté en una caja y que las cuatro formen un rectángulo. El primer esquema es el que se corresponde con el ejemplo anterior: XY-XP-YP-p. Alternando la posición de XY llegamos a los otros esquemas XP-XY-p-YP, YP-p-XY-XP y p-YP-XP-XY.
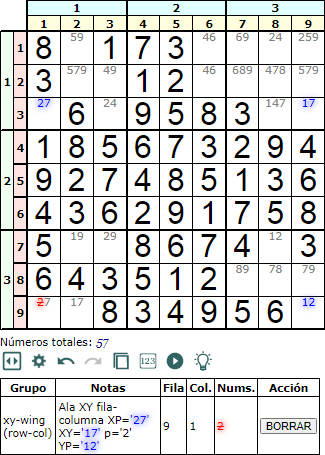
En la Figura vemos otro ejemplo con la disposición XP-XY-p-YP. Las cajas ahora no son contiguas.

En la Figura vemos una disposición YP-p-XY-XP.
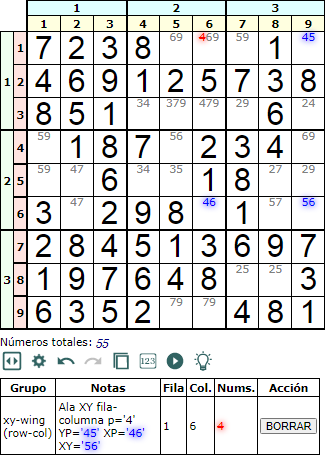
Finalmente en la Figura vemos una disposición p-YP-XP-XY.