Ala XYZ (XYZ-wing)

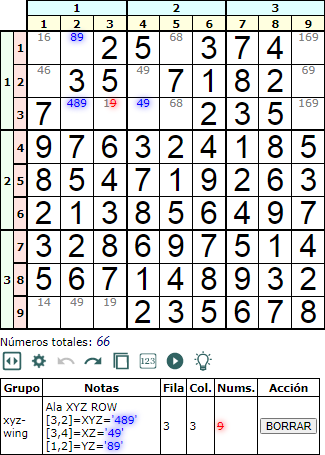
La técnica de resolución (o profundizado) de un Sudoku denominada Ala XYZ (XYZ-Wing) se basa en tres celdas que contengan los disponibles (pencil marks) XYZ, XZ e YZ. En la Figura puede ver un ejemplo con las tres celdas [3,2] = XYZ = '489', [3,4] = XZ = '49' y [1,2] = YZ = '89'. Se trata de un Ala XYZ en fila, involucrando dos cajas en la misma banda, no necesariamente contiguas.

Recuerde que una banda (band) es una fila de cajas y una pila (stack) es una columna de cajas. En una caja encontraremos XYZ = '489' e YZ = '89' en distintas filas y en cualquier columna dentro de esa caja. En la otra caja, contigua a la derecha en este caso, encontraremos XZ = '49' en la misma fila que XYZ. En estas condiciones el número z = '9' puede ser eliminado de las dos celdas de la fila dentro de la caja donde se encuentra XYZ.

Ya hemos visto las técnicas X-Wing, XY-Wing y ahora XYZ-Wing. Las letras X, Y y Z hacen referencia a los números que podemos encontrar en las celdas. En X-Wing intervenía un único número X en cuatro celdas, en XY-Wing eran dos números X e Y en tres celdas y en XYZ-Wing intervienen ahora tres números X, Y y Z en tres celdas.

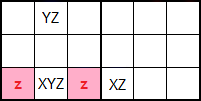
En la Figura puede ver el esquema del Ala XYZ en fila del ejemplo anterior. Se razona su corrección tomando valores alternativos para XYZ. Si en esa celda ponemos X entonces en la celda XZ habremos de poner Z por estar en la misma fila, lo que conduce a que podamos eliminar los disponibles z de las celdas adyacentes a XYZ. En cambio si en XYZ ponemos Y entonces en YZ irá Z por lo que también se pueden eliminar las z por estar en la misma caja. Por último, si en XYZ ponemos Z también podemos eliminar z por estar en la misma caja también.

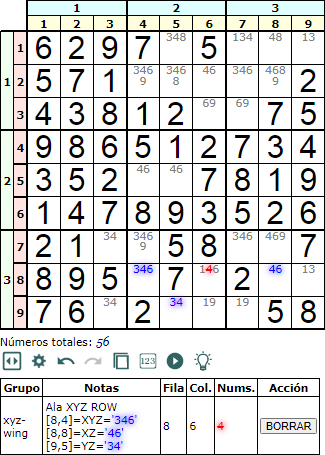
XYZ e YZ no han de estar necesariamente en la misma columna. En la Figura vemos que XYZ = '346' e YZ = '34' están en distinta columna.

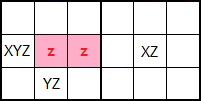
En la Figura se observa el esquema del ejemplo. Vea que esta disposición es parecida a la que vimos en el tema anterior para la técnica Ala XY del subtipo cajas, donde ahí se establecía que debían estar obligatoriamente en distintas columnas. Pero ahora en el Ala XYZ esto no es obligatorio.

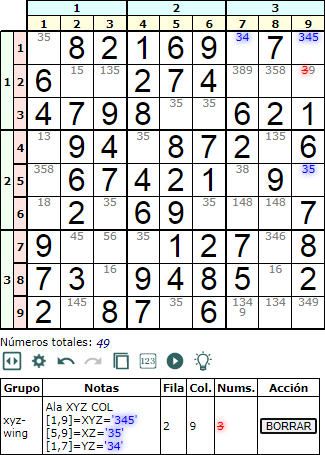
Si las cajas se localizan en una pila, entonces hablamos de Ala XY en columna. En la Figura puede ver un ejemplo. Tenemos [1,9] = XYZ = '345' y [1,7] = YZ = '34' en una caja y en la misma fila en este caso. Y en otra contigua inferior tenemos [5,9] = XZ = '35' en la misma columna que XYZ. El valor z = '3' puede ser eliminado en la celda [2,9].

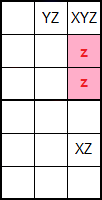
En la Figura puede ver el esquema de este ejemplo de Ala XYZ en columna (XYZ-Wing column), con XYZ e YZ en la misma fila.

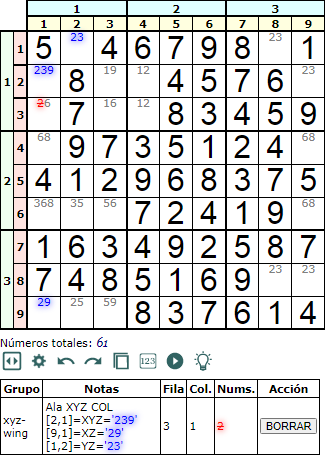
En la Figura tenemos otro ejemplo de Ala XYZ en columna, ahora en dos cajas no contiguas en la misma pila. Observe también que XYZ = '239' e YZ = '23' no están ahora en la misma fila.

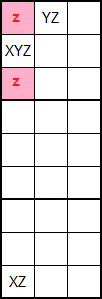
En la Figura puede ver el esquema de este ejemplo de Ala XYZ en columna, con XYZ e YZ en distintas filas.

Ala W (W-wing)

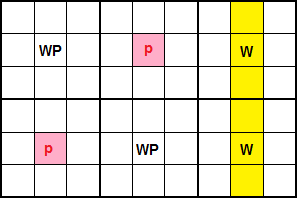
La técnica Ala W (W-Wing) involucra dos cajas, una fila o columna y dos números W y P. Según su disposición pueden dar lugar seis posibles casos. El primero de la Figura es el caso de dos cajas en la misma banda y una fila. Tenemos dos cajas a la derecha de la banda superior que tienen cada una la pareja WP = '12' en distintas filas. Por otro lado se localizan dos celdas que contengan entre sus disponibles el número W = '2', celdas ubicadas en las mismas columnas que WP y en cualquier fila a excepción de las que contienen WP='12'.

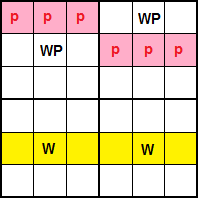
En el esquema de la Figura puede ver una disposición genérica de este caso de cajas en la misma banda y fila. WP está en dos filas distintas de dos cajas contiguas o no, pero en la misma banda. La fila resaltada en amarillo, donde localizaremos las dos W, puede ser cualquiera a excepción de las que ocupan WP. En esa fila localizamos W en las mismas columnas que WP. Es imprescindible que el número W sólo aparezca en los disponibles de esas dos celdas de esa fila amarilla. Si esto se cumple podemos eliminar los disponibles p en las celdas resaltadas de color rojo.

El razonamiento se basa en que si en alguna de las dos celdas con W='2' (celdas que tienen más disponibles) optamos por este valor, entonces en WP='12' en la misma columna hemos de poner P='1' (P es el pivote) y por tanto se eliminan los p='1' de las celdas resaltadas en rojo en su misma caja y en la misma fila de la otra caja.

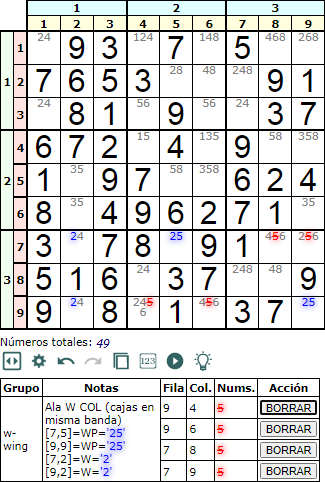
Es una técnica potente que puede solucionar muchos Sudokus. En el del ejemplo vemos que al eliminar un p='1' en la celda [2,5] nos queda el único solitario '2', lo que llevará a completar el resto del Sudoku solo con únicos solitarios.

En la Figura puede ver un Ala W en cajas en la misma banda y columna. Decimos "columna" puesto que ahora las W se localizan en una columna. WP='25' está en dos cajas en la última banda, en distintas filas. Mientras que W='2' se encuentra en la segunda columna, en la mismas filas que WP. Se observa que el '2' es único en esas dos celdas [7,2] y [7,9] de dicha columna. Podemos eliminar p='5' en las celdas [7,8], [7,9], [9,4] y [9,6].

El esquema genérico siguiente representa el ejemplo, donde las cajas con WP (no necesariamente contiguas) están en la misma banda. Y la columna con W resaltada en amarillo es cualquiera a excepción de las que ocupan WP.

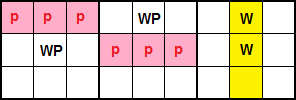
El caso que vemos en la Figura es de un Ala W en cajas la misma pila y con selección de W en una fila. Es como el anterior pero ahora buscamos W='3' en una fila, en las mismas columnas que WP='36'.

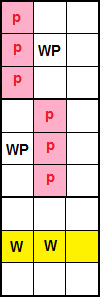
En la Figura tenemos el caso de un Ala W en cajas en la misma pila y con selección de W en una columna.

Los casos anteriores eran para WP localizados en la misma banda o pila. En esos casos podíamos eliminar hasta 6 números. Aún nos faltan dos casos por analizar que son cuando los WP se encuentran en cajas que no estén en la misma banda o pila.

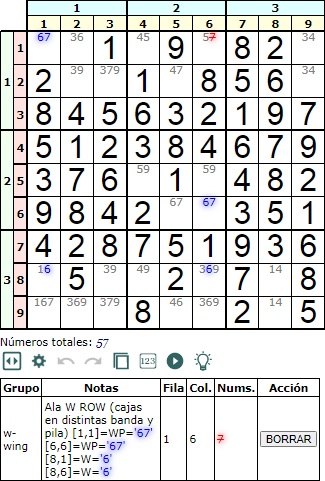
En la Figura vemos un Ala W en cajas en distintas banda y pila con selección de W en una fila. Vease que en estos casos podemos eliminar como máximo dos números, los que están en la intersección del rectángulo que vemos en el esquema.

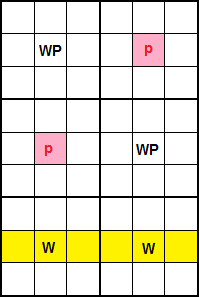
Observe como siempre que W se localiza en una fila donde W='6' sólo se encuentran en las celdas de esa fila donde se localizan los dos W.

El razonamiento de su corrección se basa en que si en una de las celdas que contiene W (recordemos que en esas celdas hay más disponibles) optamos por ese número, entonces en el WP en la misma columna irá P, con lo que los números p en la misma columna y fila no podrán ir ahí. Lo mismo sucede con el otro W.

El último caso de la Figura es de un Ala W en cajas en distintas banda y pila con selección de W en una columna.