Ala WXYZ tipo I (WXYZ-wing type I)

La técnica de resolución o profundizado de un Sudoku denominada Ala WXYZ (WXYZ Wing) se basa en cuatro celdas y cuatro números W, X, Y, Z. Hay dos tipos de Ala WXYZ. En la Figura puede ver un ejemplo del tipo I. La celda [3,1] contiene los disponibles WXYZ, que puestos en orden de aparición resulta XZWY='1235'. Mientras que la celda [2,1] contiene los disponibles ZW='23'. Estas dos celdas se deben localizar en la misma caja para el tipo I. La celda principal es la que contiene WXYZ y comparte W='3' y Z='2' con la celda WZ, siendo necesario que comparta al menos una de las dos, W o Z. La celda WXYZ puede contener entre 2 y 4 números W, X, Y o Z, pero al menos debe contener W o Z necesariamente.

Las otras dos celdas deben contener XYZ ubicadas en la misma fila que WXYZ pero no en la misma caja que WXYZ. Pueden aparecer ambas XYZ en la misma caja, como el ejemplo anterior, teniendo los mismos disponibles XZY='125'. En general podrían tener entre 2 y 3 números de valores X, Y o Z, sin que puedan contener W. Si se dan estas condiciones podemos eliminar los disponibles Z que aparezcan en las celdas contiguas a WXYZ horizontales de la caja. Tal como se observa en la Figura, podemos borrar el Z='2' de la celda [3,2].

Razonamos sobre la corrección del ejemplo tomando los números de XZWY='1235'. Si en '1235' ponemos el '1', entonces la pareja '125' queda como '25', de tal forma que pasa a ser una pareja con dos disponibles en esa fila. Tanto el '2' como el '5' deben ir en esas dos celdas necesariamente, eliminándose de otras apariciones en la fila. Por eso podemos borrar el disponible '2' de la celda [3,2]. Si en '1235' ponemos '2' entonces podemos borrar el '2' en los disponibles de la caja y por tanto el de la celda [3,2]. Si en '1235' ponemos '3' entonces la celda '23' queda '2', pudiendo también borrar el '2' en los disponibles de la caja. Por último si en '1235' ponemos '5' la pareja '125' queda como una pareja '12', volviéndose al caso de una pareja que permite borrar el '2'.

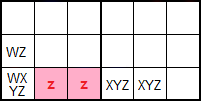
El esquema de la Figura representa el ejemplo anterior. Para razonar sobre la corrección de esta técnica tomaremos los números de WXYZ. Si en la celda donde esta WXYZ ponemos Z no podrían ir los z en las celdas resaltadas por estar en la misma caja. Si en WXYZ ponemos W, entonces en la celda WZ irá Z y por tanto no es posible z en las celdas resaltadas por estar en la misma caja. Si en WXYZ ponemos X entonces las dos celdas con XYZ quedan como dos celdas con YZ, tratándose de una pareja en la fila con lo que los números Y y Z deben ir necesariamente en esa pareja, pudiendo eliminarse las z resaltadas. De igual forma sucede si ponemos Y en WXYZ.

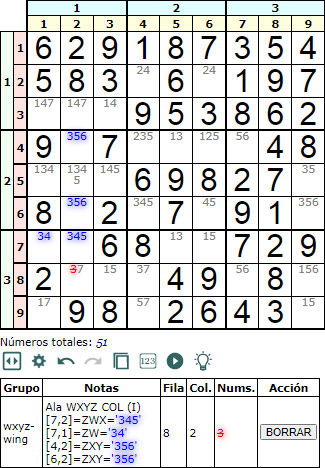
En la Figura se observa un Ala WXYZ en columna. La celda principal WXYZ tiene ahora sólo tres números ZWX='345'. La celda ZW='34' están en la misma caja. Mientras que las dos celdas ZXY='356' están en la misma columna que la celda principal. El esquema siguiente refleja el ejemplo.

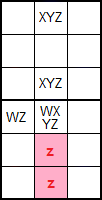
El razonamiento de su corrección es igual que el que hicimos antes. Si en la celda principal '345' ponemos '3' entonces podemos borrar el '3' disponible en la celda [8,2] por estar en la misma caja. Si en cambio en '345' ponemos '4' entonces en '34' queda '3', borrándose el '3' también de la caja. Por último si ponemos '5', las dos celdas '356' quedan como una pareja '36', con lo que podemos borrar el '3' por estar en la misma columna.

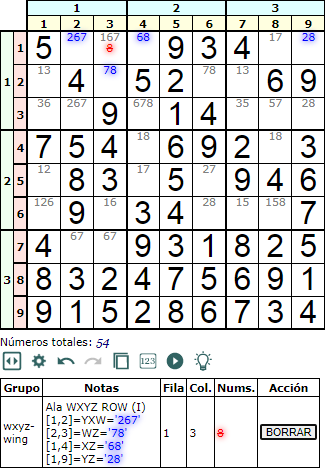
En la Figura podemos ver otro Ala WXYZ en fila, con WXYZ con tres números YXW='267', observándose que no contiene Z pero si W. Recordemos que WXYZ debe contener necesariamente W y/o Z, siendo optativo X e Y. En cambio XYZ no debe contener W, pero puede omitirse X o Y. En el ejemplo tenemos XZ='68' e YZ='28', ambos con solo dos números.

Si en '267' ponemos '2' entonces en '28' va '8' borrándose el '8' de la celda [1,3] por estar en la misma fila. Si en '267' ponemos '6' entonces en '68' va '8' borrándose también el '8' de la celda [1,3] por estar en la misma fila. Por último si en '267' ponemos '7' entonces en '78' va '8' borrándose el '8' de la celda [1,3] por estar en la misma caja.

Ala WXYZ tipo II (WXYZ-wing type II)

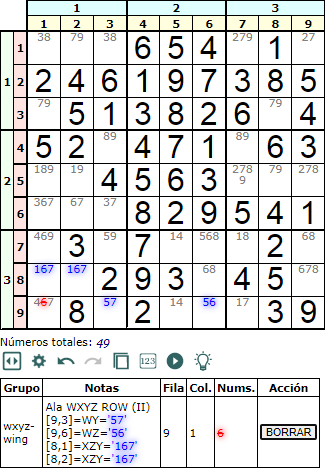
Un ejemplo de Ala WXYZ fila tipo II (WXYZ-wing row type II) se observa en la Figura. La celda principal WXYZ es en este caso WY='57' con sólo dos números. Como para el tipo I, esta celda principal puede contener entre dos y cuatro números, siendo obligatorio que contenga al menos W o Z. Este tipo II ubica la celda WZ en la misma fila que WXYZ pero en otra caja. En cambio las dos celdas XYZ se ubican ahora dentro de la misma caja que WXYZ. El esquema siguiente refleja esto.

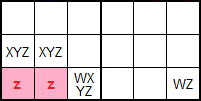
Si en la celda principal '57' ponemos '5' entonces en '56' va '6', borrándose el '6' de la celda [9,1] en la misma fila. Si en '57' ponemos '7' entonces la pareja '167 pasa a ser la pareja '16', borrándose el '6' de la celda [9,1] por estar en la misma caja.

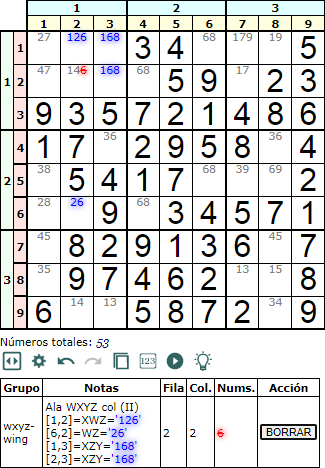
En la Figura tenemos un ejemplo de un Ala WXYZ del tipo II en columna, con el siguiente esquema:

La celda principal WXYZ tiene en este caso tres números XWZ='126'. La celda WZ está en la misma columna que WXYZ. Las dos celdas XYZ están en la misma caja que WXYZ. En estas condiciones podemos borrar el disponible z resaltado.

Si en '126' ponemos '1' entonces en la pareja '168' queda como una pareja '68', pudiendo borrar el '6' de la celda [2,1] al estar en la misma caja que la pareja. Si en '126' ponemos '2' entonces en '26' queda '6', borrando el '6' de la columna. Por último si en '126' ponemos '6' borramos el '6' por estar en la misma caja