Combinatoria con recursivos: Combine Tools

Combinatoria: Combine Tools

  
Muestras
El primer valor son las iteraciones y el segundo es el resultado de la fórmula. Ambos deben ser iguales.
Configuración
La función para copiar Arrays puede afectar al tiempo de ejecución. Puede cambiar el método de copia en la configuración. La función copy2() se utiliza en los algoritmos de partición.
Vista del resultado

Combinaciones

Las combinaciones de una lista con n elementos son todas las sublistas con k elementos distintos que se pueden extraer sin importar el orden. Se denotan como (nk), C(n, k) y también como Cn,k.

Número de sublistas:
C(n, k) =n!
k!(n-k)!
Base matemática:
C(n, k) = C(n-1, k-1) + C(n-1, k)
Sublistas generadas:
Tiempo:
Iteraciones: (Sin coste de copia)
Coste calculado (Sin coste de copia):
T(n, k) = 2 ( ∑j=0..k C(n, j) ) - 1 =
Código JS: Llamar con combine1(list, k)
// C(n, k) = C(n-1, k-1) + C(n-1, k)
function combine1(list=[], k=0, n=list.length, res=[], result=[], n0=list.length){
    if (k===0){
        result.push(copy(res));
    } else if (n>0) {
        res.push(list[n0-n]);
        combine1(list, k-1, n-1, res, result);
        res.pop();
        combine1(list, k, n-1, res, result);
    }
    return result;
}
Trazado

Factorial

Las permutaciones de una lista con n elementos distintos son todas las sublistas ordenadas con n elementos distintos que se pueden generar. Se denota generamente como P(n) y su valor es P(n) = n! denominado el factorial. Se calcula recursivamente con n! = n (n-1)!.
0! = 1,
n! = n × (n-1)!
// n! = n * (n-1)!
function factorial(n){
    if (n<=0){
        return 1;
    } else {
        return n*factorial(n-1);
    }
}
Versión: 2024-06-01

Aplicación Combinatoria

Figura
Figura. Combinatorics Tool

La combinatoria estudia la forma de generar todas las posibles sublistas de una lista de elementos. En el fondo se trata de contar elementos. Los métodos principales son las combinaciones, permutaciones y variaciones de una lista de elementos. Vea que el problema es generar el conjunto de sublistas más que calcular el valor númerico de esas funciones. Ya hace tiempo analicé el coste de permutar un Array. En esa serie de temas veíamos como resolver recurrencias para calcular el coste de algoritmos recursivos usando técnicas como el desarrollo o la ecuación característica. A raíz de necesitar las combinaciones de una lista de dígitos para la aplicación Sudoku, me planteé estudiar más a fondo estas funciones combinatorias.

Para analizar una función combinatoria como C(n, k) podemos utilizar la técnica de la función generadora o generatriz. Esta aplicación servirá para comprobar los resultados matemáticos alcanzados en cada caso. Con esta aplicación se incluyen una serie de temas que analizan el coste de las funciones combinatorias. El tema inicial Funciones de generación para resolver recurrencias es una introducción a esa materia, repitiendo algunos problemas que ya resolvimos con desarrollos o ecuación característica.

En el tema Resumen funciones combinatorias recopilamos toda la información que aparece en la aplicación, separada en dos partes:

  1. Funciones combinatorias que generan listas, recopilando las funciones que vemos en la pestaña "Listas" de la aplicación.
  2. Funciones combinatorias numéricas, recopilando las funciones que vemos en la pestaña "Numéricos" de la aplicación.
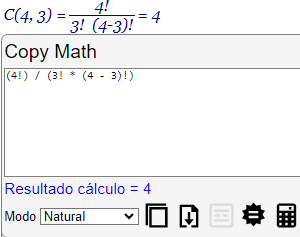
Figura
Figura. Copy Math

El nuevo componente Copy Math nos permite ver la expresión en lenguaje natural de una fórmula, explicándose lo relacionado con las funciones combinatorias con más detalle en el tema Muestras de fórmulas matemáticas.