06 jul 2023

Escribir fórmulas matemáticas en HTML

Versiones

Versión Math 2023-12-03_10-16 donde se incluyen estilos _vc, _vs y _xn, mejorando _xc para definiciones de funciones a trozos con uso de la función Piecewise. Versión Copy Math 2023-12-03_10-20 donde se incluyen las configuraciones usar Piecewise, que se explica en definiciones de funciones. Y otra para configurar la altura de los contenedores.
Versiones Math 2023-07-08_21-40 y Copy Math 2023-07-09_10-13 iniciales.

Recursos para escribir fórmulas matemáticas en una página web

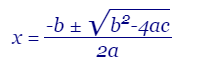
Desde hace tiempo he necesitado presentar fórmulas matemáticas en estas páginas web. Aunque existe la extensión MathML, de la que luego hablaremos, HTML ofrece pocas cosas para hacerlo directamente. He venido usando algunos recursos como los elementos SUB y SUP. Por ejemplo x²+1, con el código <var>x<sup>2</sup>+1</var>. El elemento VAR tiene fuente Georgia y estilo itálica para intentar lograr una apariencia de fórmula matemática. Sin embargo, escribir fracciones, raíces o cosas más complejas con solo estos recursos y con una presentación aceptable no es fácil.

Ahora, con la serie de temas que exponen la Combinatoria con recursivos, he implementado los módulos JavaScript Math y CopyMath. En la Figura puede ver una fórmula matemática escrita en HTML directamente en esta página, con estilo CSS. Antes de entrar a explicar estos módulos veamos que otros recursos existen y sus ventajas o inconvenientes.

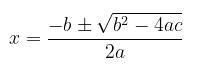
LaTeX (latex-project.org) es el recurso que mejor resultado visual produce, como se observa en la Figura. Pero su resultado es una imagen, no es HTML ni texto. La obtuve en codecogs, un editor on-line usando la siguiente entrada en código Latex que produce la imagen anterior:

x = \frac{-b\pm\sqrt{b^{2}-4ac}}{2a}

El código no parece díficil de aprender. Sin estudiarlo se observa que frac es fracción y sqrt es raíz cuadrada. Para las potencias se usa ^, algo que suele usarse en lenguaje natural para escribir expresiones matemáticas en texto plano. No es díficil averiguar que pm se refiere al signo plus minus (± ± en HTML).

Pero ese código Latex no está en esta página web. Lo que está es la Figura, una imagen. Y uno de los objetivos que tengo es que podamos obtener con JavaScript la expresión matemática en lenguaje natural a partir del HTML en la página. Más abajo explicaremos el motivo de esta necesidad.

El siguiente paso es intentarlo con la extensión de HTML MathML. La siguiente fórmula está implementada usando ese recurso. Se verá correctamente si su navegador soporta MathML.

x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}

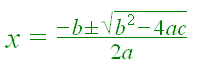
En 2011 hice una prueba en el tema El elemento html en HTML-5, comprobando que en ese momento sólo lo soportaba Firefox, como se observa en la Figura, imagen que capturé en aquel momento.

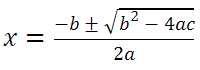
En este momento también es soportado en Chrome, como se observa en la Figura.

Y este es el código, ejemplo que también puede observar en MathML3:

<math style="font-size: 1.7em">
    <mi>x</mi>
    <mo>=</mo>
    <mfrac>
        <mrow>
            <mo form="prefix">−</mo> <mi>b</mi> <mo>±</mo>
            <msqrt>
                <msup> <mi>b</mi> <mn>2</mn> </msup>
                <mo>−</mo>
                <mn>4</mn> <mo>&#8290;</mo> <mi>a</mi> <mo>&#8290;</mo> <mi>c</mi>
            </msqrt>
        </mrow>
        <mrow>
            <mn>2</mn> <mo>&#8290;</mo> <mi>a</mi>
        </mrow>
    </mfrac>
</math>

Nuevamente, sin estudiar MathML, se obseva que se pueden identificar los componentes. MI es una variable, MFRAC es una fracción, MROW es una fila, MO es un operador, MN es un número, MSUP es un super-índice. JavaScript podría leer ese HTML, que ahora sí que está en esta página. Pero me parece muy extenso debido a la necesidad de indicar cada componente de la expresión por separado.

Módulos Math y Copy Math para presentar fórmulas matemáticas en HTML

Veamos como el módulo Math reduce el tamaño del código. Esta es la fórmula de la Figura 1 escrita en HTML y con estilo CSS aportado por el módulo Math:


x =	-b ± √b²-4ac
	2a

Este es el código HTML que he escrito para que se presente esa fórmula, cuyo estilo CSS es insertado (directa o indirectamente) en esta página web (esto lo veremos más adelante):

<table class="math">
    <tr><td rowspan="3">x =</td>
        <td>-b ± <i class="_fs150">√</i><i class="_bt _pt20 _ml15">b<sup>2</sup>-4ac</i></td>
    </tr>
    <tr><th></th></tr>
    <tr><td>2a</td></tr>
</table>

Obviamente es mucho menos código que usando MathML. Pero la funcionalidad que quiero conseguir se obtiene con el módulo Copy Math. Al hacer doble-click sobre la fórmula se abre un panel emergente que nos permite extraer la fórmula en lenguaje natural, ofreciendo el siguiente resultado:

x = (- b + sqrt(b^2 - 4ac)) / (2a), x = (- b - sqrt(b^2 - 4ac)) / (2a)

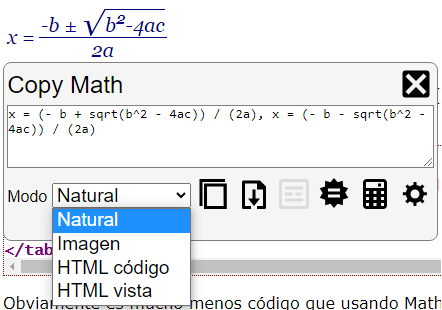
En la Figura se observa el panel emergente Copy Math, donde vemos que podemos obtener la expresión en lenguaje natural, una imagen, el propio HTML código escrito en esta página y, por último, el HTML vista que viene a ser el HTML+CSS para copiar o exportar e insertarlo en otra página.

Antes de seguir conviene aclarar que este componente Copy Math no es un editor de fórmulas. El texto que aparece no es modificable. Incluso el código HTML obtenido de la página tampoco puede modificarse antes de exportarlo. Su único objetivo es que el usuario pueda copiar o exportar esa fórmula en varios formatos. Por ahora la forma en que las edito es escribirlas directamente, sobre la marcha, en el entorno de desarrollo donde edito estas páginas. Y reconozco que para eso es necesario saber algo de HTML, especialmente del elemento TABLE. Y algo más de CSS. Es posible implementar una herramienta para editar fórmulas sin necesidad de conocer en profundidad HTML y CSS. Pero por ahora no lo voy a hacer, pues mi objetivo actual es sólo escribir fórmulas en una página web sin tener que usar Latex o MathML, como expliqué más arriba.

Con el botón con el icono de Wolfram Alpha, o bien copiando la expresión en lenguaje natural, podemos editarla en esa potente herramienta. En este enlace podrá observarlo en WolframAlpha.

En la Figura puede ver el resultado, observando que es necesario convertir el símbolo "±" en dos expresiones. Esto es así pues una función o expresión no puede tener valores alternativos en sus argumentos, de tal forma que si pasamos "±" Wolfram Alpha nos dirá que no entiende la consulta.

Y esta es la ventaja que me aporta esta utilidad Copy Math, pues cuando estuve estudiando el coste de los algoritmos para resolver problemas de Combinatoria con recursivos, tuve que usar recursos como Wolfram Alpha para aprender algo o confirmar los resultados obtenidos. Con esta utilidad puede escribir la expresión en HTML mientras estoy editando la página y, al mismo tiempo, obtenerla en lenguaje natural para comprobar su presentación y, lo que es más importante, su evaluación y análisis en Wolfram Alpha.

Esta aplicación prepara enlaces para ser evaluados en Wolfram Alpha, recurso que es de uso libre para propósitos no comerciales, como es el caso de este sitio Wextensible.com. Puede comprobar los términos de uso de Wolfram Alpha.

Utilidades de Copy Math

Para finalizar este tema explicaremos las utilidades de Copy Math para extraer la expresión en lenguaje natural, imagen o HTML. En el próximo tema explicaremos como funciona el módulo Math, que es el que contiene el CSS y sólo se encarga de presentar visualmente el HTML.

En la primera barra tenemos estos botones:

Copiar contenidos de texto
Los contenidos de texto se puede copiar en el portapapeles.
Descargar texto o imagen
Los contenidos de texto se descargan en archivo TXT, la vista previa en archivo de texto HTML y la imagen en archivo PNG.
Vista previa del HTML y CSS
La vista previa abre una nueva ventana del navegador para mostrar la vista HTML.
Abrir Wolfram Alpha para evaluar expresión
Redirige a la web de Wolfram Alpha para evaluar la expresión.
Calcular con el módulo propio calc.js
En aquellas páginas que cargue el módulo Calculadora (calc.js), se mostrará este botón. Ejecutará el cálculo de la expresión en lenguaje natural, siempre y cuando contenga parámetros con valores que ese módulo pueda calcular. En otro caso se mostrará el error.
Si además se carga el módulo calcui.js que es una interfaz para presentar una calculadora que usa calc.js, se abrirá esta aplicación con la expresión preparada para su ejecución. Puede ver un ejemplo en el siguiente tema.
Por ejemplo, con la expresión que resuelve la ecuación x²-2x-15 = 0 obtenemos las soluciones 5, -3 que son dos valores separados por coma, pudiendo comprobarlo activando con doble click sobre esta expresión y pulsar el botón de calcular:
(2 ± √(-2)²-4×1×(-15)) ÷ (2×1)
Observe que para el producto podemos usar alternativamente "*" o "×" y para la división "/" o "÷".
Abrir panel de configuración
Al pulsar en configuración se abre un panel con estos botones secundarios
- Información
  Abre un panel con información de los módulos Math y Copy Math.
- Cambiar idioma
  Cambia idioma de la interfaz entre español e inglés.
- Maximizar ancho
  Maximiza el ancho disponible.
- Actualizar tras aplicar configuración
  La configuración modifica la presentación, actualizando el resultado con este botón. En los apartados siguientes veremos las disponibles en este momento.

Configuración usar funciones naturales y chequear paréntesis

Usar funciones naturales: La fórmula √(2) se muestra con la expresión sqrt(2), pues sqrt es el nombre de la función ampliamente reconocida en lenguaje natural para la raíz cuadrada. Pero si desmarcamos esta configuración se muestra como fue escrita en el HTML, es decir, √(2). Wolfram Alpha es capaz de reconocer ambas versiones, pero no así el modulo Calc ni otras aplicaciones.

Las funciones en lenguaje natural que se traduce son √: sqrt, ∛: cuberoot, ∑: sum, Γ: gamma, ∏: product, ∫: integral, nombres que Wolfram Alpha reconoce. También se traducen otras expresiones:

(nk) = C(n, k)
|x| = abs(x)
⌈x⌉ = ceil(x)
⌊x⌋ = floor(x)
n^k = pochhammer(n, k)
n^k = factorialpower(n, k)
!n = subfactorial(n)

Con chequear paréntesis se comprueban si están bien anidados. Por ejemplo, con la expresión 2 + (3-1)) / (5-2) nos dará error de que hay un paréntesis de cierre sin apertura.

Configuración incluir JavaScript en HTML vista

La vista previa HTML construye un documento HTML pudiendo descargarlo o con el botón vista previa HTML verlo funcionar en una ventana aparte. Por defecto sólo se usa CSS para presentar la expresión. Por ejemplo, vea esta presentación:

x + y

El HTML que he escrito en esta página es el siguiente:

<div class="math">x + <i class="_bo">y</i></div>

El segundo sumando de la expresión aparece con borde porque se aporta la clase _bo. Estas clases que se gestionan en el módulo Math siempre empiezan con guion bajo y a continuación tiene 2 letras iniciales del estilo, en la medida de lo posible identificables con el estilo CSS, que en este caso es border: currentColor solid 0.0625em. Vea ahora esta modificación:

x + y

El HTML que he escrito en esta página es el siguiente:

<div class="math">x + <i class="_bo _fs150 _pa30">y</i></div>

Hemos agregado las clases _fs150 y _pa30, la primera aporta font-size: 1.5em y la segunda padding: 0.3em. Se trata de algunas propiedades con la estructura guion bajo, 2 letras y 1 a 3 dígitos. En estos casos el módulo Math se encarga de convertir esta clase en un atributo style que insertará en el elemento ya existente en la página. Este es el código que finalmente se renderiza en el navegador:

<div class="math">x + <i class="_fs150 _bo _pa30" 
style="font-size: 1.5em; padding: 0.3em;">y</i></div>

Observe como Math convierte las clases _fs150 y _pa30 en estilo en línea en el elemento con style="font-size: 1.5em; padding: 0.3em;". Lo que hace Math es tomar el número de la clase, dividirlo entre 100 y agregar "em".

Cuando sacamos la vista previa lo hacemos por defecto con esta conversión ya hecha. A no ser que usemos la opción de incluir JavaScript en la vista previa. En este caso se exporta también el JavaScript de tal forma que la conversión se realiza cuando se cargue la página de vista previa. En el tema siguiente explicaremos esto más a fondo.

Configuración bordes y otras

Una presentación a exportar como imagen o como HTML podemos dotarle de un borde exterior, como el redondeado que aparece en la Figura. Además si el elemento usado es un TABLE, también podemos poner bordes en celdas interiores, como también se observa en esta imagen. Esto nos puede servir para ver como está estructurada la tabla, espcialmente cuando hay celdas combinadas.

El borde exterior se selecciona entre sólido, punteado, rayado, doble y redondeado. Los bordes de las celdas sólo se mostrarán como punteados, pues de hecho en lugar de bordes son contornos, que se corresponde con el estilo outline de CSS.

La configuración Usar Piecewise tiene que ver con la extracción en lenguaje natural de funciones definidas así. Ver más en el tema siguiente, en el apartado Piecewise.

La configuración Altura permite modificar la altura de los contenedores de texto o imagen.