Permutar un Array
Marzo 2023: En la aplicación Combinatoria se agrupan algoritmos para obtener combinaciones, permutaciones y variaciones, con y sin repetición. Se incluyen los algoritmos para obtener permutaciones que exponemos en este tema.
El problema de construir permutaciones
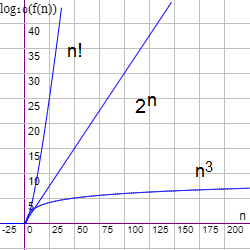
Cuando un algoritmo tiene un coste factorial es prácticamente inutilizable para valores no muy grandes. En la Figura puede ver las funciones n3, 2n y n! El eje Y está en graduación logarítmica, de tal forma que los valores marcados son 105, 1010, 1015, 1020, ... En temas anteriores vimos costes lineales, cuadráticos y exponenciales como el representado en la gráfica con la función 2n. Visualmente es evidente que n! es extremadamente costoso con respecto a los otros. Y el problema de permutar un conjunto de n elementos es que se obtienen n! permutaciones, teniendo un coste que no parece que pueda ser inferior a O((n+1)!) como veremos en este tema.
Si observa n=25 verá que su factorial cruza en 1025, más exactamente 25! = 1.551×1025. En comparación con 253 = 1.563×104 y con 225 = 3.355×107, estos resultan insignificantes con respecto al factorial. Si un algoritmo tarda 1 μs en ejecutar una iteración y el algoritmo tiene un coste de 25! iteraciones, tomará un tiempo de 10-6 × 1.551×1025 = 1.551×1019 segundos, dividido entre 3.1536×107 segundos que tiene un año resultan 4.9×1011 años. Si pudiéramos bajar el coste hasta 14!, el algoritmo se ejecutaría aproximadamente en un día. Y si lo bajamos a 13! lo resolveríamos en algo menos de dos horas. Y necesitaríamos menos de cuatro segundos si conseguimos un coste de 10! Con esto se observa lo que queremos decir con "valores grandes" para el factorial: crece muy rápido desde valores pequeños del tamaño del problema.
Y esto es lo que pasa con el problema de construir permutaciones. Con una lista de n elementos se generan n! permutaciones. Si el algoritmo recibe un Array con 25 elementos de tipo number y nos dicen que tenemos que construir otro Array que contenga los resultados de 25! permutaciones, es evidente que no hay ordenador actualmente que soporte el manejo de ese Array con 1.551×1025 elementos. El ordenador se quedará sin memoria muchísimo antes. Si cada elemento ocupa un byte (cosa que dudo pues un registro tipo number de JavaScript ocupa 8 bytes), esa cantidad supone 1.551×1013 TB (Terabytes). Con 13! ocuparía unos 6.2 GB (Gigabytes). Mi ordenador tiene una RAM de 8 GB y con unos ejemplos que veremos más abajo no podemos pasar de un tamaño 9 del problema porque pasa precisamente eso, el navegador se queda sin memoria.
Podría ser diferente si no necesitasemos almacenar los resultados en memoria, por ejemplo dando salida a una impresora o escribiendo en un disco cada vez que generemos una permutación. Esto evitaría colapsar la memoria RAM, pero ocasionaría un retraso en la ejecución del algoritmo dado que las operaciones de escribir en una salida son más lentas que las escrituras en memoria. En un ejemplo más abajo volveremos a comentar sobre esto.
Permutar un Array con un recursivo
Hace años necesité construir con PHP las permutaciones de una lista de palabras para la ejecución de un buscador interno. Si teníamos una lista de palabras como "bordes", "tabla" en cualquier orden, teníamos que generar la expresión regular /bordes.*?tabla|tabla.*?bordes/i. En definitiva necesitamos construir las permutaciones de ese array de palabras uniendo cada permutación con el separador ".*?" y, finalmente, unir el Array resultante con "|".
Supongamos que tenemos una lista de letras. Partimos de la base de que sabemos permutar estos casos triviales:
lista = []: Permutaciones =[]lista = ["a"]: Permutaciones =[["a"]]lista = ["a", "b"]: Permutaciones =[["a", "b"], ["b", "a"]]
Como ejemplo y de forma esquemática vamos a permutar ["a", "b", "c"], con lo que finalmente tendríamos que obtener 6 permutaciones como [["a", "b", "c"], ..., ["c", "b", "a"]] (recordar que el número de permutaciones de n elementos es n!). Si tiene más de 2 elementos, iteramos por ellos tomando uno fijo y permutando el resto de elementos. En este caso el resto son 2, por lo que ya este es un caso trivial y basta intercambiar esos 2 elementos. Entonces componemos ("⊕") ese elemento con los que vienen de la permutación menor. Lo siguiente expresa de forma esquemática el proceso:
permutar(a, b) = 0 --> ab, ba permutar(a, b, c) = 0 --> a ⊕ permutar(b, c) = a ⊕ (bc, cb) => abc, acb 1 --> b ⊕ permutar(a, c) = b ⊕ (ac, ca) => bac, bca 2 --> c ⊕ permutar(a, b) = c ⊕ (ab, ba) => cab, cba
Vease que se cumplen las dos condiciones para hacer un recusivo. Existe al menos un caso trivial y tenemos una recurrencia, de tal forma que el problema se va disminuyendo de tamaño en cada llamada.
Convirtamos el recursivo hecho en PHP a JavaScript. Generalizamos el problema para que devuelva las permutaciones como Arrays. Si es necesario al final unir sus elementos como vimos más arriba, bastaría hacer algo como lo siguiente con el resultado final que devuelve el recursivo:
let res = permutar(lista);
res = res.map(v => v.join(".*?")).join("|");El código del recursivo es el siguiente:
function permutar(lista){
let n = lista.length;
let result = [];
if (n<2) {
result = [...lista]; // (* Ver nota)
} else if (n===2) {
result = [[lista[0], lista[1]], [lista[1], lista[0]]];
} else {
for (let j=0; j<n; j++) {
let listaMenor = lista.slice(0,j).concat(lista.slice(j+1));
let subResult = permutar(listaMenor);
for (let i=0; i<subResult.length; i++){
result.push([lista[j], ...subResult[i]]);
}
}
}
return result;
}Si la lista inicial tiene menos de 2 elementos devuelve una copia de la lista (*). Si tiene 2 elementos devuelve un Array con copias de la lista y en orden inverso. Si tiene más de 2 elementos entramos en el proceso comentado antes. En este algoritmo hay métodos de Array que pueden ocultar el coste intrínseco. Para analizar el algoritmo vamos a reemplazarlos con bucles. Haremos uso de declaraciones de Arrays con coste unitario y del método push() que también tiene coste unitario:
function permutar(lista){
numCall++;
numIter++;
let n = lista.length;
let result = [];
if (n<2) {
result = [...lista]; // (* Ver nota)
} else if (n===2) {
result = [[lista[0], lista[1]], [lista[1], lista[0]]];
} else {
for (let j=0; j<n; j++) { //B1
numIter++;
let listaMenor = [];
for (let k=0; k<n; k++){ //B2
numIter++;
if (k!==j) listaMenor.push(lista[k]);
}
let subResult = permutar(listaMenor);
for (let i=0; i<subResult.length; i++){ //B3
numIter++;
let s = [];
s.push(lista[j]);
for (let k=0; k<subResult[i].length; k++){ //B4
numIter++;
s.push(subResult[i][k]);
}
result.push(s);
}
}
}
return result;
}Ejemplo: Permutar Array con un recursivo
permutar(lista):Estudiemos el coste:
- En la entrada del recursivo hemos puesto un contador de iteraciones que acumula la secuencia de operaciones simples que están al inicio y las comparaciones de los condicionales.
- Los casos triviales ejecutan operaciones simples, que en secuencia con las operaciones del inicio y comparaciones resulta unitario. Con n<2 suponemos que devolvemos la propia lista y no una copia (*).
- En el caso no trivial se produce un bucle B1 de longitud n que más su cabecera acaba con un coste de n+1. El coste unitario de la cabecera de este bucle se combina en secuencia con el coste de entrada del recursivo.
- Dentro del bucle B1 tenemos una operación simple para declarar
listaMenory dos cabeceras de bucles B2 y B3, cuyo coste combinado en secuencia es unitario. - El bucle B2 de longitud n tiene un coste n. Este bucle construye una lista con n-1 elementos, pero itera sobre n elementos. Su cabecera se combina en secuencia con la declaración de
listaMenor. - La llamada se hace con
listaMenory es por tanto sobre un tamaño n-1. - Esta llamada a la permutación con una lista de longitud n-1 produciría una lista subresultado de longitud (n-1)! permutaciones. Por lo tanto el bucle B3 tiene una longitud de (n-1)! Su cabecera se combina en secuencia con la cabecera del bucle anterior y la operación simple que declara
listaMenor. - El bucle interior B4 itera sobre sobre subresultados cuyo tamaño es n-1, puesto que una lista menor de n-1 elementos producirá n-1! subresultados, cada uno de ellos con una permutación de tamaño n-1.
Desarrollando la definición:
T(n) = 1 + B1 = = 1 + n ( T(n-1) + 1 + B2 + B3 ) = = 1 + n ( T(n-1) + 1 + B2 + (n-1)! (1 + B4) ) = = 1 + n ( T(n-1) + 1 + n + (n-1)! (1+n-1) ) = = n T(n-1) + n2 + n + 1 + n (n-1)! n = n T(n-1) + n2 + n + 1 + n n!Nos queda finalmente:
| T(n) = | { | 1 | si n≤2 |
| n T(n-1) + n2 + n + 1 + n n! | si n>2 |
Esta recurrencia no parece ser equiparable al modelo que vimos en el tema anterior:
a0tn+a1tn-1+...+aktn-k = bnp(n)En estos casos hay que buscar otra forma de resolver la recurrencia. Una de ellas es desarrollarlas desde n hasta el caso trivial. Para simplificar sustituiremos P(n) = n2 + n + 1 y lo repondremos al finalizar:
En la iteración n tenemos:
T(n) = n T(n-1) + P(n) + n n!Iteración n-1
T(n) = n ( (n-1) T(n-2) + P(n-1) + (n-1) (n-1)! ) + P(n) + n n! = = n(n-1) T(n-2) + n P(n-1) + P(n) + n (n-1) (n-1)! + n n! = = n(n-1) T(n-2) + n P(n-1) + P(n) + (n-1) n! + n n!Iteración n-2
T(n) = n(n-1) ( (n-2) T(n-3) + P(n-2) + (n-2) (n-2)! ) + n P(n-1) + P(n) + (n-1) n! + n n! = = n(n-1)(n-2) T(n-3) + n(n-1)P(n-2) + n P(n-1) + P(n) + (n-2) n! + (n-1) n! + n n!Seguimos iterando hasta llegar a la iteración 3
T(n) = n(n-1)(n-2)···4·3 T(2) + + n(n-1)···5·4 P(3)+···+n(n-1)P(n-2)+n P(n-1)+P(n) + +∑k=3..n (n-k+3) n!Hemos llegado al caso trivial donde T(2) = 1 y como ∑k=3..n (n-k+3) n!= 1/2 (n2+n-6) n!
T(n) = n!/2 + ( ∑k=3..n (n!/k!) P(k) ) + 1/2 (n2+n-6) n!Reponiendo P(k) = k2+k+1
T(n) = n!/2 + ( n! ∑k=3..n (k2+k+1)/k! ) + 1/2 (n2+n-6) n!Y finalmente lo ponemos como sigue
T(n) = n! ( 1/2 (n2+n-5) + ∑k=3..n (k2+k+1)/k! )Para implementar este coste calculado en el ejemplo usamos dos funciones auxiliares. Una de ellas es factorial(n) que ya vimos en los temas iniciales de esta serie. La otra es sum(n) que ejecutará el sumatorio:
// n!
function factorial(n){
if (n===0){
return 1;
} else {
return n*factorial(n-1);
}
}
// ∑(k=3..n) (k^2+k+1)/k!
function sum(n){
let suma = 0;
for (let k=3; k<=n; k++){
suma += (k**2+k+1)/factorial(k);
}
return suma;
}
if (n<2) {
coste = 1;
} else {
coste = Math.round(factorial(n)*((n**2+n-5)/2+sum(n)));
}
Comprobamos que este coste calculado coincide con el que calcula el contador numIter.
Coste asintótico del recursivo para permutar
Veamos ahora cuál es el coste asintótico del recursivo anterior:
T(n) = n! ( 1/2 (n2+n-5) + ∑k=3..n (k2+k+1)/k! )Primero observamos la posible convergencia de la serie:
∑k=3..∞ (k2+k+1)/k!Para ello utilizaremos el criterio del cociente, para lo cual analizamos la relación entre dos términos sucesivos:
limk→∞ ak+1 / ak = L ∈ [0, +∞]- Si L<1 la serie converge,
- Si L>1 o L=∞ la serie no converge,
- Si L=1 el criterio no establece nada respecto a su convergencia
Aplicándolo a nuestra serie tenemos
limk→∞ (((k+1)2+(k+1)+1)/(k+1)!) / ((k2+k+1)/k!) = = limk→∞ ((k+1)2+k+2)/((k2+k+1)(k+1)) = 0Como el numerador es un polinomio de grado 2 y el denominador de grado 3, vemos que el límite es 0. Al ser L<1 la serie converge. Podemos decir que existe un c ∈ ℝ+ tal que c > 2 ∑k=3..n (k2+k+1)/k!. Con esto podemos acotar el coste calculado:
T(n) = n! ( 1/2 (n2+n-5) + ∑k=3..n (k2+k+1)/k! ) < n! ( 1/2 (n2+n-5) + c/2 ) = = 1/2 n! (n2+n+c-5)Es obvio que n2 > (n+c-5) para valores grandes de n, por lo que n! n2 es el término que domina el coste. Por otro lado n2 n! < (n+2)(n+1)n! por lo que se deduce n2 n! < (n+2)!, resultando que T(n) ∈ O((n+2)!). Podemos corroborarlo con la regla del límite que recordamos a continuación:
- Si limn→∞ f(n)/g(n) ∈ ℝ+ entonces f(n) ∈ O(g(n)) y g(n) ∈ O(f(n))
- Si limn→∞ f(n)/g(n) = 0 entonces f(n) ∈ O(g(n)) pero g(n) ∉ O(f(n))
- Si limn→∞ f(n)/g(n) = +∞ entonces f(n) ∉ O(g(n)) pero g(n) ∈ O(f(n))
Pero antes de aplicar esto calcularemos la suma de la serie usando WolframAlpha
c = ∑k=3..∞ (k2+k+1)/k! = 4 e - 15/2 = 3.37312...Resolver directamente
Ajustemos cada término para que quede en un rango que empiece en cero:
- ∑k=3..n 1/(k-2)! = - 1/(2-2)! + ∑k=2..n 1/(k-2)! = - 1 + ∑k=0..n-2 1/k!
- ∑k=3..n 1/(k-1)! = - 1/(1-1)! - 1/(2-1)! + ∑k=1..n 1/(k-1)! = - 2 + ∑k=0..n-1 1/k!
- ∑k=3..n 1/k! = - 1/0! - 1/1! - 1/2! + ∑k=0..n 1/k! = - 5/2 + ∑k=0..n 1/k!
Como ∑k=0..∞ 1/k! = e (ver MathWorld Alpha o Wikipedia) nos queda que la serie converge a
c = -1 + e + 2 (-2 + e) - 5/2 + e = 4e - 15/2Quedando T(n) = 1/2 n! (n2+n+c-5) = 1/2 n! (n2+n+4e-25/2). Aplicamos ahora la regla del límite anterior comparando f(n) = T(n) con g(n) = (n+1)! y también con g(n) = (n+2)!
Como limn→∞ 1/2 n! (n2+n+4e-25/2)/(n+1)! = ∞ entonces T(n) ∉ O((n+1)!)
Como limn→∞ 1/2 n! (n2+n+4e-25/2)/(n+2)! = 1/2 ∈ ℝ+ entonces T(n) ∈ O((n+2)!)
Permutar con el Algoritmo de Heap
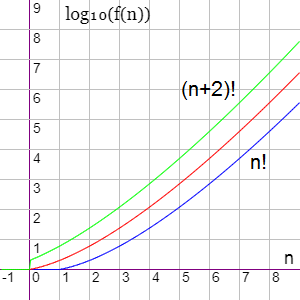
Ya sabíamos que hay n! permutaciones con una lista de n elementos. Por lo tanto el coste de generarlas no parece que pueda ser inferior a n! Pero entre n! y (n+2)! que obtuvimos antes hay un buen escalón. ¿Podemos conseguir un coste de (n+1)! al menos? Por ejemplo, bajar de 9! = 362880 a 8! = 40320 supone evitarnos 322560 iteraciones: cerca del 89% menos. Con ningún otro tipo de coste, ni siquiera el exponencial, supone tanto ahorro bajar una unidad de orden de coste.
Olvidemos por un momento los recursivos y la permutaciones y analicemos el siguiente algoritmo. Se trata de crear un Array de longitud n! con elementos que también son Array que contienen un cierto valor n veces. El coste de este algoritmo es 1 + B1 = 1 + n! (1 + B2) = 1 + n! (1 + n B3) = 1 + n! + n n! B3. Si createValue(n) tiene un coste unitario, nos queda entonces 1 + n! + n n!, donde n n! es el término que domina el coste. Como n! < n n! < (n+1)! esto supone un coste de O((n+1)!) Y esto no hay forma de reducirlo.
let array = [];
for (var i=0; i<n!; i++){ // B1
let temp = [];
for (var j=0; j<n; j++){ // B2
let value = createValue(j); // B3
temp[j].push(value);
}
array.push(temp);
}Si tenemos que generar y devolver n! Arrays de longitud n cada uno con una permutación, yo no veo forma de hacerlo con un coste inferior O((n+1)!) aún en el caso que el coste de generar un permutación sea unitario. Así que el objetivo es generar las permutaciones con el menor coste posible, lo que equivale a tener el menor coste posible para la función createValue() del bucle anterior, con la finalidad de que el coste final no se aparte de O((n+1)!).
Los algoritmos de intercambio como el algoritmo de Heap son al parecer los más eficientes en este sentido. El código implementado en JavaScript sería como esto:
function permutarHeap(lista, n=lista.length){
if (n<=1) {
output(lista);
} else {
for (let i=0; i<n; i++){
permutarHeap(lista, n-1);
if (i<n-1) {
if (n%2===0){
[lista[i], lista[n-1]] = [lista[n-1], lista[i]];
} else {
[lista[0], lista[n-1]] = [lista[n-1], lista[0]];
}
}
}
}
}Se trata de intercambiar elementos modificando el Array de la lista inicial. Cuando se llegue a un caso trivial tendremos en lista una permutación y la devolvemos. Supuestamente existirá una función output(lista) que devuelve el Array con una permutación. Pero esa función no existe en JavaScript. Podría ser una salida a impresora o a otro dispositivo, pero en JavaScript esto no es posible puesto que el recursivo debe terminar para que cualquier interacción con el exterior de la función se actualice. Incluso en el caso de que ahí pudiera producirse una salida hacia el exterior de la función de una permutación, no puede considerarse que no tiene coste o que el coste sea unitario.
Para entenderlo implementaremos ese algoritmo omitiendo eso del output. Para ello haremos una inmersión de resultados que mantenemos en un argumento. El Array result está vacío con la primera llamada y cada vez que lleguemos a un caso trivial meteremos una nueva permutación. Al hacer las llamadas lo pasaremos como argumento y así mantenemos el Array siempre actualizado. Cuando el recursivo finalice lo devolveremos.
Usaremos una opción copy que es una variable global para devolver la lista tal como está o bien hacer una copia. Ya hemos dicho que los Array se pasan por referencia entre llamadas, de tal forma que si no hacemos una copia siempre tendremos la misma referencia al Array inicial, es decir, la lista con la que iniciamos el recursivo. Si no hacemos copia el coste de agregar la lista a result sera unitario. Pero si hacemos una copia el coste será el tamaño de la lista, es decir n, pues ese tamaño siempre es el mismo para todas las permutaciones.
La otra opción que podemos usar es heap. Esto nos permitirá usar el Algoritmo de Heap u otra versión parecida que he visto en Internet. Las dos tienen el mismo coste en número de iteraciones registradas en el contador numIter, pero usaremos esa segunda versión para hacer los cálculos de coste.
let numIter = 0, numTriv = 0, copy = true, heap = true;
function permutarHeap(lista, n=lista.length, result=[]){
numIter++;
if (n<=1) {
if (copy) {
let s = [];
for (let i=0; i<lista.length; i++){
numTriv++;
s.push(lista[i]);
}
result.push(s);
} else {
result.push(lista);
}
} else {
if (heap) {
for (let i=0; i<n; i++){
numIter++;
permutarHeap(lista, n-1, result);
if (i<n-1) {
if (n%2===0){
[lista[i], lista[n-1]] = [lista[n-1], lista[i]];
} else {
[lista[0], lista[n-1]] = [lista[n-1], lista[0]];
}
}
}
} else {
for (let i=n-1; i>-1; i--){
numIter++;
[lista[i], lista[n-1]] = [lista[n-1], lista[i]];
permutarHeap(lista, n-1, result);
[lista[i], lista[n-1]] = [lista[n-1], lista[i]];
}
}
}
return result;
}Ejemplo: Algoritmo Heap para permutar
permutarHeap(lista):Como hemos dicho vamos a usar la segunda versión para hacer los cálculos de coste. El algoritmo con sólo la segunda versión y sin devolver una copia de la lista sería el siguiente:
function permutarHeap(lista, n=lista.length, result=[]){
numIter++;
if (n<=1) {
result.push(lista);
} else {
for (let i=n-1; i>-1; i--){
numIter++;
[lista[i], lista[n-1]] = [lista[n-1], lista[i]];
permutarHeap(lista, n-1, result);
[lista[i], lista[n-1]] = [lista[n-1], lista[i]];
}
}
return result;
}El caso trivial tiene coste unitario. El no trivial tiene el coste del comparativo de entrada más un bucle de tamaño n. Su interior es la suma de un coste unitario por las dos sentencias de intercambio que están en secuencia y la nueva llamada a permutar:
1 + n (1 + T(n-1))La definición de la recurrencia de coste queda así:
| T(n) = | { | 1 | si n≤1 |
| n T(n-1) + n + 1 | si n>1 |
Desplegamos algunos términos para obtener una solución. En la iteración n al inicio tenemos:
T(n) = n T(n-1) + n + 1Iteración n-1:
T(n) = n ((n-1) T(n-2) + (n-1) + 1) + n + 1 = n (n-1) T(n-2) + n(n-1) + 2 n + 1Iteración n-2:
T(n) = n(n-1) ((n-2) T(n-3) + (n-2) + 1) + n(n-1) + 2 n + 1 = = n(n-1)(n-2) T(n-3) + n(n-1)(n-2) + 2 n(n-1) + 2 n + 1Iteración n-3:
T(n) = n(n-1)(n-2) ((n-3) T(n-2) + (n-3) + 1) + n(n-1)(n-2) + 2 n(n-1) + 2 n + 1 = = n(n-1)(n-2)(n-3) T(n-4) + n(n-1)(n-2)(n-3) + 2 n(n-1)(n-2) + 2 n(n-1) + 2 n + 1Seguimos hasta alcanzar la iteración 2
T(n) = n(n-1)(n-2)···3·2 T(1) + n(n-1)(n-2)···3·2 + 2n(n-1)(n-2)···4·3 + ··· + 2n(n-1)(n-2) + 2n(n-1) + 2n + 1Lo resaltado en azul tiene los términos del rango [2..n-1]. El caso trivial es T(1) = 1, con lo que los dos resaltes en amarillo son iguales:
T(n) = 2n(n-1)(n-2)···3·2 + 2n(n-1)(n-2)···4·3 + ··· + 2n(n-1)(n-2) + 2n(n-1) + 2n + 1Vemos que lo resaltado en amarillo sigue la secuencia de la serie con rango [2..n-1] resaltada en azul, por lo que podemos agruparlos en una serie que se incrementa en un término con el rango ahora [2..n]:
T(n) = 1 + 2 (n(n-1)(n-2)···3·2 + ··· + n(n-1)(n-2) + n(n-1) + n)Deducimos el término general como n!/(n-k+1)! con k ∈ [2..n] quedando:
T(n) = 1 + 2 ∑k=2..n n!/(n-k+1)!Extraemos n! fuera del sumatorio, pues no depende de k:
T(n) = 1 + 2 n! ∑k=2..n 1/(n-k+1)!El sumatorio lo implementamos con este código:
// ∑(k=2..n) 1/(n-k+1)!
function sumHeap(n){
let suma = 0;
for (let k=2; k<=n; k++){
suma += 1/factorial(n-k+1);
}
return suma;
}Con 1+2*factorial(n)*sumHeap(n) obtenemos el coste calculado que ponemos en el ejemplo, comprobándose que coincide con el contador de iteraciones numIter. En el ejemplo este es el coste con la opción copy desactivada.
Coste asintótico del recursivo Heap para permutar (sin coste de copiar)
Calculemos el coste asintótico del recursivo Heap que acabamos de obtener:
T(n) = 1 + 2 n! ∑k=2..n 1/(n-k+1)!Primero hemos de analizar la convergencia de la serie. Podemos usar WolframAlpha para ver que la serie converge a e-1:
limn→∞ ∑k=2..n 1/(n-k+1)! = e-1Pero si queremos deducirlo nosotros, primero hemos de arreglar el n dentro del término 1/(n-k+1)! Para ello haremos un cambio de variable:
j = n-k+1 ⇒ k = n-j+1 k ∈ [2..n] ⇒ j ∈ [n-1..1] ⇒ j ∈ [1..n-1]Aplicando este cambio:
∑k=2..n 1/(n-k+1)! = ∑j=1..n-1 1/j! = (∑j=0..n-1 1/j!) - 1/0! = (∑j=0..n-1 1/j!)-1Sucede que ∑j=0..∞ 1/j! = e (ver MathWorld Alpha o Wikipedia) con lo que la serie converge a e-1. Con esto el coste tiene esa cota superior
T(n) = 1 + 2 n! ∑k=2..n 1/(n-k+1)! < 1 + 2 n! (e-1) ⇒ T(n) ∈ O(n!)Hemos conseguido reducir el coste desde O((n+2)!) hasta O(n!), pero bajo la hipótesis de no utilizar la opción para copiar el resultado, con lo que realmente obtenemos n! resultados iguales a la lista de partida y no las n! permutaciones. Vamos a ver en el siguiente apartado el coste con la opción de copiar activada, que al final es lo que estamos buscando.
Coste asintótico del recursivo Heap para permutar (con coste de copiar)
Recordemos como era el recursivo, donde copy es una variable global con valor booleano que fijamos antes de la primera llamada externa al recursivo:
function permutarHeap(lista, n=lista.length, result=[]){
numIter++;
if (n<=1) {
if (copy) {
let s = [];
for (let i=0; i<lista.length; i++){
numTriv++;
s.push(lista[i]);
}
result.push(s);
} else {
result.push(lista);
}
} else {
...
}
return result;
}Vamos a calcular el coste cuando copy = true. Para copiar la lista podíamos haber utilizado el operador de propagación de JavaScript. Habría que sumar lista.length al acumulador de iteraciones triviales numTriv, con lo que el número de iteraciones triviales serán las mismas:
if (copy) {
numTriv += lista.length;
result.push([...lista]);
}Para calcular el coste de iteraciones y el asintótico supusimos en el apartado anterior que el coste trivial era unitario, lo que ejecutábamos haciendo copy = false antes de iniciar el ejemplo. Pero el ejemplo tiene que devolver un Array con las permutaciones también en un Array. Cuando llegamos a n=1 tendremos en lista una nueva permutación que acumulamos en el Array result.
Pero hemos de copiar lista para pasarlo a result, puesto que de otra forma acabaremos con la misma permutacion inicial repetida n! veces, dado que JavaScript devuelve los Array por referencia y no por valor. El coste de copiar un Array es su tamaño. Como hay n! casos triviales dado que tenemos que generar n! permutaciones, el coste total de los casos triviales es n×n!. Así que el coste final es:
Vemos que hemos rebajado hasta O((n+1)!) cuando el del primer apartado era O((n+2)!). En la siguiente tabla resumimos el primer recursivo (R1), el segundo con el Heap sin coste de copiar cada permutación (R2) y el tercero será ese mismo Heap con el coste de copiar (R3). Anotamos el tiempo de ejecución y el número de iteraciones totales para un tamaño n=9:
| Nº | Recurrencia | Coste calculado | Coste acotado | Coste asintótico | Iteraciones para n=9 | Tiempo (ms) para n=9 |
|---|---|---|---|---|---|---|
| R1 | T(1) = 1, T(n) = n T(n-1) + n2 + n + 1 + n! | T(n) = n! ( 1/2 (n2+n-5) + ∑k=3..n (k2+k+1)/k! ) | T(n) < 1/2 n! (n2+n+4e-25/2) | T(n) ∈ O((n+2)!) | 16646428 | 290 |
| R2 | T(1) = 1, T(n) = n T(n-1) + n + 1 | T(n) = 1 + 2 n! ∑k=2..n 1/(n-k+1)! | T(n) < 1 + 2 n! (e-1) | T(n) ∈ O(n!) | 1247059 | 23 |
| R3 | T(1) = n n!, T(n) = n T(n-1) + n + 1 | T(n) = n n! + 1 + 2 n! ∑k=2..n 1/(n-k+1)! | T(n) < n n! + 1 + 2 n! (e-1) | T(n) ∈ O((n+1)!) | 4512979 | 85 |
El algoritmo R2 no es nada realista pues no contempla el coste de construir el resultado. Pero hemos conseguido rebajar el coste de R1 desde unos 290 ms hasta 85 ms de R3 para un tamaño de 9 elementos. Supone una reducción aproximada de 71% en tiempo y de un 73% en iteraciones.