Algoritmos iterativos y recursivos

Los algoritmos pueden clasificarse en iterativos y recursivos. Dentro de la primera clase podemos incluir los bucles como while o for. Por otro lado los recursivos son funciones que se llaman a sí mismas para conseguir el resultado. Cuando nos iniciamos con la programación preferimos los iterativos, pues son, en principio, más fáciles de entender. Puede que parezca más sencillo seguir la secuencia de acontecimientos dentro de un bucle que dentro de un recursivo.

La mayor parte de las veces podemos resolver los problemas con iterativos. Pero en otros casos la recursividad nos permitirá resolver el problema con un razonamiento más simple e intuitivo. Haremos ejemplos de uso en JavaScript, empezando en este tema por explicar las nociones generales sobre recursivos. En los siguientes veremos recursivos que reducen el tamaño del problema mediante substracción y mediante división (los conocidos divide y vencerás). También expondremos recursivos que no se incluyen en esos casos, como Fibonacci o generar permutaciones. Y otros que nos permiten recorrer una estructura de árbol. Finalmente veremos recursivos en algoritmos del tipo vuelta atrás.

El factorial

Para empezar a exponer que es un recursivo utilizaremos uno de los más sencillos. El factorial de un número entero no negativo se calcula con n! = n×(n-1)×(n-2)×...×3×2×1. Para calcular factorial(n) podríamos iterar una variable m ∈ [1, n], iniciando una variable parcial r = 1 donde acumularíamos r = m × r en cada iteración del bucle. Al final del bucle tendríamos en r el resultado:

function factorialx(n){
    //console.trace(n);
    let r = 1;
    for (let m=1; m<=n; m++){
        r = m * r;
    }
    return r;
}

Observe que en el código anterior se contempla el caso trivial cuando n = 0. Vemos que no entraríamos en el bucle for, con lo que el resultado sería r = 1, resultado correcto puesto que matemáticamente el factorial de cero es uno.

Resolvamos el problema con un recursivo. Para ello hemos de tener claro lo siguiente:

1. El problema debe tener al menos un caso trivial o caso base que no requiera cálculos o bien ese cálculo sea muy simple.
2. El problema debe reducirse en cada nueva llamada hasta llegar al caso trivial.

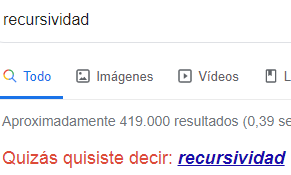
Es crucial que el tamaño del problema se reduzca y llegue al caso trivial para conseguir el resultado. Pues en otro caso tendremos un bucle indefinido, como la broma del buscador de Google que capturamos en la Figura, donde al buscar el término "recursividad" nos sugiere el enlace "Quizás quisiste decir: recursividad", lo que conduce a un bucle sin fin.

Con el factorial el caso base es cuando n = 0, limitándonos a devolver un uno. Por otro lado el problema se reduce viendo que n! = n × (n-1)! es una forma recurrente de expresarlo, observando que el problema se reduce de n a n-1. Teniendo estas dos cosas claras pasamos a codificar nuestro factorial recursivo:

function factorial(n){
    //console.trace(n);
    if (n===0){
        return 1;
    } else {
        return n*factorial(n-1);
    }
}

Este código del recursivo es más intuitivo que el del iterativo. Si entendemos la recurrencia y el caso base, es fácil ver como se resuelve el problema sin tener que visualizar el interior del bucle implícito que hay en el recursivo. Esto puede no parecer importante con este problema del factorial. Pero cuando el problema es muy complejo puede ser más fácil pensar en términos de recursividad para buscar una solución.

De hecho cuando pensamos en un recursivo nos olvidamos de la secuencia interna de iteraciones. Sólo nos centramos en el caso base y en la recurrencia. Y aunque en este tema pondremos ejemplos trazando lo que pasa dentro de un recursivo, cuando uno se acostumbra a usarlos se olvida (y debe olvidarse) de intentar seguir o trazar lo que pasa en su interior.

Limitaciones y rendimiento de un recursivo

Sin embargo muchas veces en programación contar con un código más simple e intuitivo supone una merma de rendimiento. Y este es el caso de los recursivos. Cuando JavaScript ejecuta una función crea un contexto para su ejecución. Se trata de almacenar en memoria todas aquellas variables a las que la función referencia. Las funciones en ejecución se van apilando en el orden en que se llaman, para luego ser desapiladas en orden inverso. Y todo esto tiene un coste añadido sobre un simple bucle iterativo.

Al inicio del código de la función recursiva del factorial del apartado anterior hemos puesto console.trace(n), que si lo des-comentamos obtendremos una traza de la pila de llamadas (call stack) de la función factorialx():

n=6
factorialx @ index.js:21
(anonymous) @ index.js:38

La primera llamada se produce en la función anónima que se usa para agregar un evento al botón de ejecución. Desde ahí se llama una única vez a factorialx(). Si por otro lado trazamos la pila de llamadas del recursivo obtenemos esto en la consola:

n=6
factorial @ index.js:47
(anonymous) @ index.js:64
n=5
factorial @ index.js:47
factorial @ index.js:51
(anonymous) @ index.js:64
n=4
factorial @ index.js:47
factorial @ index.js:51
factorial @ index.js:51
(anonymous) @ index.js:64
n=3
factorial @ index.js:47
factorial @ index.js:51
factorial @ index.js:51
factorial @ index.js:51
(anonymous) @ index.js:64
n=2
factorial @ index.js:47
factorial @ index.js:51
factorial @ index.js:51
factorial @ index.js:51
factorial @ index.js:51
(anonymous) @ index.js:64
n=1
factorial @ index.js:47
factorial @ index.js:51
factorial @ index.js:51
factorial @ index.js:51
factorial @ index.js:51
factorial @ index.js:51
(anonymous) @ index.js:64
n=0
factorial @ index.js:47
factorial @ index.js:51
factorial @ index.js:51
factorial @ index.js:51
factorial @ index.js:51
factorial @ index.js:51
factorial @ index.js:51
(anonymous) @ index.js:64

Cuando lleguemos al final con n = 0 tendremos una pila de 8 llamadas, incluyéndose la llamada de la función anónima. Por eso no hemos de olvidar que hay un máximo de pila de llamadas. Con Chrome 76 en mi navegador usando un valor a partir de n = 15683 en el recursivo obtenemos Maximum call stack size exceeded. Este valor depende del tamaño de la memoria que el navegador destina a la pila de llamadas y del tamaño del contexto que tiene que guardar.

Sin embargo con el iterativo no hay límite alguno. Aunque en el primer ejemplo hemos puesto una limitación a n = 100000 al valor que podemos introducir, realmente el iterativo podría seguir funcionando indefinidamente.

Con este ejemplo del factorial no tendríamos problemas puesto que el máximo factorial que podemos calcular es 170! = 7.257415615307994e+306, a partir de ahí obtendremos Infinity. Sin embargo el número 15683 no parece muy grande teniendo en cuenta que el contexto de la función factorial(n) es muy simple. Con un problema que genere un contexto más grande, el máximo de la pila podría ser muy pequeño para resolver el problema. Incidiremos sobre esto en el siguiente apartado.

En el siguiente ejemplo haremos un test de rendimiento entre la función recursiva e iterativa:

En Chrome 76 con n=15 el recursivo hace en torno a un 16% menos iteraciones que el iterativo. A medida que n aumenta el comportamiento del recursivo empeora. En Firefox 68 hay menos diferencia entre ambos, pero también se empeora con valores grandes de n. En cualquier caso es evidente que la pila de llamadas tiene un coste significativo. Pero esto no debe hacernos abandonar la idea de utilizar los recursivos.

Recursivos finales

Un ejemplo anterior con la función recursiva factorial(n) lo habíamos titulado como recursivo no final. Lo reproducimos otra vez a continuación:

//Recursivo NO FINAL
function factorial(n){
    if (n===0){
        return 1;
    } else {
        return n*factorial(n-1);
    }
}

Recordando que n va decreciendo y para n > 0 devolvemos la función compuesta (o expresión) n*factorial(n-1). Cuando n = 0 devolvemos el caso base 1. Esta parte con n descendiendo y JavaScript apilando funciones podemos entenderla como parte de bajada del recursivo. A partir del caso base ya no se producen más llamadas y JavaScript empezará a desapilar las funciones resolviendo ahora la función compuesta. Esta parte la podemos denominar subida del recursivo. Así cuando finalice la subida devolverá el último valor que será el resultado final acumulado. Para que ese mecanismo funcione es imprescindible que exista un mecanismo de pila que vaya guardando los valores anteriores, para posteriormente ejecutar la composición de funciones en el desapilado.

Si evitamos la función compuesta podemos obtener el valor final en la bajada del recursivo. Para ello debemos almacenar los resultados parciales en algún sitio, como en un parámetro de la propia función. La siguiente función ffactorial(n) obtiene el mismo resultado que la anterior:

//Recursivo FINAL
function ffactorial(n, r=1){
    if (n===0){
        return r;
    } else {
        return ffactorial(n-1, r*n);
    }
}

Es este un recursivo final porque cuando lleguemos al caso base tendremos el valor final. De hecho todo el "trabajo" se realiza en la bajada, pues en la subida JavaScript se limitará a desapilar funciones sin que afecte al resultado. Eliminar la función compuesta trasladando su acción a un argumento no siempre es fácil de hacer. Pero podrían haber algunas ventajas al usar una recursivo final frente a un no final.

En el siguiente ejemplo podrá comparar ambos recursivos utilizando n = 6:

El ejemplo toma lectura del valor de n y del resultado al inicio de la función para la bajada y al final de la función para la subida. Para ello modificamos ambas funciones para recoger esa traza:

let traceDown = [], traceUp = [];
function factorialTrace(n){
    traceDown.push([n, "?"]);
    let result;
    if (n===0){
        result = 1;
    } else {
        result = n*factorialTrace(n-1);
    }
    traceUp.push([n, result]);
    return result;
}
let tracefDown = [], tracefUp = [];
function ffactorialTrace(n, r=1){
    tracefDown.push([n, r]);
    let result;
    if (n===0){
        result = r;
    } else {
        result = ffactorialTrace(n-1, r*n);
    }
    tracefUp.push([n, result]);
    return result;
}

Obtenemos una traza como la siguiente:

BAJANDO:
n=6, result=?
n=5, result=?
n=4, result=?
n=3, result=?
n=2, result=?
n=1, result=?
n=0, result=?

SUBIENDO:
n=0, result=1
n=1, result=1
n=2, result=2
n=3, result=6
n=4, result=24
n=5, result=120
n=6, result=720

BAJANDO:
n=6, result=1
n=5, result=6
n=4, result=30
n=3, result=120
n=2, result=360
n=1, result=720
n=0, result=720

SUBIENDO:
n=0, result=720
n=1, result=720
n=2, result=720
n=3, result=720
n=4, result=720
n=5, result=720
n=6, result=720

En el recursivo no final factorial(6) el resultado 720 se obtiene al final de la fase de subida. Durante la bajada el resultado ni siquiera está definido, por eso le ponemos un "?". Mientras que en el recursivo final ffactorial(6) se obtiene al final de la bajada y el resultado si está definido en esta fase pues viene en un argumento. Durante la subida el resultado no se modifica. Si eso es así ¿podría haber una solución para evitar la pila de llamadas, y por tanto su coste asociado, dado que este recursivo final sólo "trabaja" durante la bajada?

La respuesta es sí, pero a medias. Antes debemos saber que la expresiones función recursiva final y no final la veremos en documentación en inglés como tail recursive function y nontail recursive function. Algo como nontail call y tail call se refiere a llamadas a funciones no finales y finales, en el sentido de si la llamada está sola o inmersa en una expresión respectivamente.

ES6 quiso implementar la mejora de las recursivos finales para no incrementar la pila de llamadas, lo que llama Proper Tail Calls (PTC), de tal forma que las llamadas que están en posición final (solas, no inmersas en una expresión) no crearán contextos que incrementen la pila de llamadas. La propuesta que puede ver en Syntactic Tail Calls (STC) se basa en utilizar algo como la palabra clave continue que identifique que esa llamada no debe ser apilada:

//Recursivo FINAL con PTC
function ffactorial(n, r=1){
    if (n===0){
        return r;
    } else {
        return continue ffactorial(n-1, r*n);
    }
}

Sin embargo a fecha actual la mayor parte de los navegadores no lo implementan. En la tabla de compatibilidad ES6 puede ver esto en la entrada proper tail calls (tail call optimisation).

Transformar un recursivo en un iterativo

Un recursivo puede transformarse en un iterativo. Esto es importante saberlo por si tenemos problemas al implementar un recursivo por alguna razón. En el caso del recursivo no final dará lugar a dos bucles. El primer bucle se dedica a la bajada modificando el valor de m=n hasta llegar al valor del caso base m=0. En ese momento fijamos el resultado del caso base (r = 1). Partiendo de ese valor de m entramos en el segundo bucle que producirá la subida donde se calculará de forma acumulada el resultado.

function factorial(n){
    if (n===0){
        return 1;
    } else {
        return n*factorial(n-1);
    }
}

function factorialb(n){
    let m = n;
    while (m>0){
        m = m - 1;
    }
    let r = 1;
    while (m<n){
        m = m + 1;
        r = m * r;
    }
    return r;
}

El primer bucle anterior parece innecesario, pues bastaría con sustituirlo por m = 0. Pero esto no será siempre tan evidente y con otros problemas tendremos que iterar en este primer bucle para resolver el valor de m que fija el caso base.

El recursivo final se transforma en un único bucle, el de bajada. Y esta es otra de las ventajas de que el recursivo sea final. El resultado del caso base r = 1 queda fijado antes de entrar en el bucle. Al finalizar el bucle tendremos el resultado acumulado.

function ffactorial(n, r=1){
    if (n===0){
        return r;
    } else {
        return ffactorial(n-1, r*n);
    }
}

function ffactorialb(n){
    let m = n, r = 1;
    while (m>0){
        r = m * r;
        m = m - 1;
    }
    return r;
}

Compare el iterativo final anterior con el primer bucle que probamos en esta página:

function factorialx(n){
    let r = 1;
    for (let m=1; m<=n; m++){
        r = m * r;
    }
    return r;
}

Funcionalmente el bucle while y este for ejecutan lo mismo: iteran en el intervalo [1, n] uno descendente y otro ascendente, pero ambos acumulando el resultado r = m*r. Podemos modificar el sentido del primer bucle haciéndolo descendente con for (let m=n; m>0; m--) comportándose exactamente igual. O incluso sustituir el bucle while del iterativo final por un bucle for.