El problema de la mochila discreta 0-1
Programación dinámica para resolver el problema de la mochila discreta 0-1
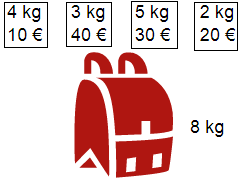
La forma en que podemos seleccionar n objetos con peso pi y valor vi para cargarlos en una mochila con un peso máximo P de tal forma que obtengamos el valor máximo V puede dar lugar a tres tipos de problemas:
1) Mochila fraccionable que maximice V donde los objetos no pueden repetirse y pueden fraccionarse para completar el peso máximo P. Se resuelve con un algoritmo voraz.
2) Mochila discreta 0-∞ que maximice V donde los objetos SI pueden repetirse y NO pueden fraccionarse para completar un peso que no supere el máximo P. Se resuelve con un algoritmo vuelta atrás.
3) Mochila discreta 0-1 que maximice V donde los objetos NO pueden repetirse y NO pueden fraccionarse para completar un peso que no supere el máximo P. Se resuelve con programación dinámica, lo que nos ocupará este tema.
Vimos que usando un algoritmo voraz no era posible obtener una solución óptima para una mochila discreta 0-1. En ese enlace vimos que usando la mochila con peso máximo 8, array de pesos [4, 3, 5, 2] y array de valores [10, 40, 30, 20] obteníamos una mochila con los objetos con índices [1, 3] (índices contando desde cero), cuyo valor total era V = 40+20 = 60 con un peso de P = 3+2 = 5 que no superaba el peso máximo de 8 kg. Sin embargo existía una solución óptima que era seleccionar los índices [1, 2] con un valor total de V = 40+30 = 70 y con un peso de P = 3+5 = 8.
Vamos a resolver este problema con programación dinámica. En primer lugar agregamos una posición cero en pesos y valores, quedando p = [0, 4, 3, 5, 2] y v = [0, 10, 40, 30, 20]. El peso máximo de la mochila es P = 8. Hemos de optimizar maximizando el valor total de la mochila (V). Necesitamos construir la tabla de resultados intermedios procediendo de una forma similar a como hicimos con el problema de devolver cambio que vimos en el tema anterior. Será una tabla con tantas filas como el array de pesos o valores y tantas columnas como el peso máximo más uno. Inicializamos esta tabla con ceros:
j→ (P) i↓ 0 1 2 3 4 5 6 7 8 ------------------------------------ 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0 4 0 0 0 0 0 0 0 0 0
La tabla anterior nos da el valor máximo, de tal forma que V[i,j] nos dice el valor máximo de una mochila si consideramos los i primeros objetos y un peso máximo j. Así que la solución al problema dado está en la posición V[4, 8] pues se consideran todos los objetos y un peso máximo de 8 kilos.
Rellenamos la tabla empezando en la posición [0, 0] y recorriéndola hacia la derecha y hacia abajo. Comprobaremos que cada posición se fundamenta en los valores de las posiciones anteriores. Esto es básico para asegurar que, si una posición anterior es óptima, la posición posterior también lo será. Se cumple así el principio de optimalidad, que dice que en una secuencia óptima de decisiones, toda subsecuencia debe ser también óptima
. Estas son las posibilidades que tenemos al rellenar cada posición:
- La fila i=0 no se modifica y queda con los ceros iniciales.
- Si i=1, la primera fila con el primer objeto, tenemos estas posibilidades:
- Si j<p[i] no hacemos nada, pues si el peso total j es menor que el peso de ese primer objeto, entonces no podemos meter ese objeto y la posición queda con el valor cero, es decir, esa mochila no tendrá ningún valor.
- Si j≥p[i] entonces V[i, j] = v[i], puesto que si j es igual o mayor que el peso de ese primer objeto, entonces el valor de la mochila contendrá ese primer objeto con su valor.
- En otro caso si i>1, para los objetos de las filas siguientes, podemos diferenciar estos casos:
- Si j<p[i] entonces V[i, j] = V[i-1, j], puesto que si ese objeto no cabe en la mochila con peso total j, el valor de la mochila será el que obtuvimos en el paso anterior en la fila i-1.
- En otro caso si j≥p[i] entoncesV[i, j] = Max(V[i-1, j], v[i] + V[i-1, j-p[i]]), puesto que caben dos posibilidades tomando la que maximice el valor:
- Que ese objeto no quepa y se tomará el valor de la fila anterior V[i-1, j]
- Que ese objeto quepa con lo que sumaremos v[i] más el valor ya calculado en la fila anterior y en la columna j-p[i] que es el resto de peso que falta por meter, es decir, v[i] + V[i-1, j-p[i]]
Tras aplicar las reglas anteriores, la tabla queda finalmente así:
j→ (P) i↓ p v 0 1 2 3 4 5 6 7 8 ----------------------------------------------- 0 0 0 0 0 0 0 0 0 0 0 0 1 4 10 0 0 0 0 10 10 10 10 10 2 3 40 0 0 0 40 40 40 40 50 50 3 5 30 0 0 0 40 40 40 40 50 70 4 2 20 0 0 20 40 40 60 60 60 70
Hemos agregado dos columnas que, aunque no forman parte de la tabla de resultados intermedios, nos sirve para identificar el peso y valor de cada uno de los objetos.
Implementando en JavaScript el problema de la mochila con programación dinámica
El código usado para implementar en JavaScript el problema de la mochila discreta 0-1 con programación dinámica es el siguiente:
function llenarMochila(pesoMaximo=0, pesos=[], valores=[]){
let values = [];
//TABLA DE RESULTADOS INTERMEDIOS: Valores máximos
numIter++;
values = pesos.map(v => Array.from({length: pesoMaximo+1}, () => 0));
for (let i=1; i<pesos.length; i++) {
numIter++;
for (let j=1; j<=pesoMaximo; j++){
numIter++;
if (i===1) {
if (j>=pesos[i]) values[i][j] = valores[i];
} else if (j<pesos[i]) {
values[i][j] = values[i-1][j];
} else {
values[i][j] = Math.max(values[i-1][j], valores[i] + values[i-1][j-pesos[i]]);
}
}
}
//BUCLE VORAZ
let objetos = [];
let j = pesoMaximo;
for (let i=pesos.length-1; i>0; i--){
numIter++;
if (values[i][j] !== values[i-1][j] && values[i][j] === values[i-1][j-pesos[i]] + valores[i]){
objetos.push(i);
j -= pesos[i];
}
}
return objetos;
}Se diferencian dos partes en el código. Una para construir la tabla de resultados intermedios en el array values, siguiendo las reglas que vimos en el apartado anterior. Ese array servirá como conjunto de entrada para la segunda parte, un bucle voraz que extrae los objetos que componen la solución y que explicaremos más abajo. En este ejemplo uso muestras de problemas que he encontrado en Internet para verificar que obtengo los mismos resultados.
Ejemplo: Mochila discreta (0-1)
llenarMochila(pesoMaximo, pesos, valores): Algoritmo voraz para deducir objetos de la mochila 0-1
| i↓ | p | v | j→ (P) | ||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 4 | 10 | 0 | 0 | 0 | 0 | 10 | 10 | 10 | 10 | 10 |
| 2 | 3 | 40 | 0 | 0 | 0 | 40 | 40 | 40 | 40 | 50 | 50 |
| 3 | 5 | 30 | 0 | 0 | 0 | 40 | 40 | 40 | 40 | 50 | 70 |
| 4 | 2 | 20 | 0 | 0 | 20 | 40 | 40 | 60 | 60 | 60 | 70 |
Cada posición de la tabla de resultados intermedios contiene el valor máximo que cabe en un mochila de un peso máximo j con i objetos. En la Figura puede ver la que se corresponde con la mochila con peso máximo 8, array de pesos [0, 4, 3, 5, 2] y array de valores [0, 10, 40, 30, 20]. Agregamos siempre en programación dinámica una posición cero a estos arrays para una correcta ejecución.
El objetivo de esta tabla es simple. Si tenemos una mochila que puede cargar un peso máximo de 8 con 4 objetos, buscamos la posición (i, j) = (4, 8) que nos dice que podemos obtener un valor máximo de 70 (la última celda inferior derecha). Con los 2 primeros objetos y un peso máximo de 5 kilos la posición (i, j) = (2, 5) nos da el valor 40. En definitiva, cada posición (i, j) nos da el valor máximo de una mochila de peso máximo j llena con objetos seleccionados entre el primero hasta el i, pero no nos dice que objetos de ese tramo 1..i componen esa mochila. Sin embargo esa información está implícita en las reglas con las que se construyó la tabla.
Se observa que hay dos posiciones marcadas con fondo azul. Son las que se detectan en el algoritmo voraz que nos sirve para deducir que objetos componen la solución para una mochila de 8 kilos de peso máximo. En este caso son los objetos con índices 2 y 3, con un peso total de 8 y un valor total de 70. La tabla de resultados intermedios sirve, por tanto, como conjunto de entrada para alimentar el voraz. Usamos la segunda parte del código que volvemos a reproducir a continuación:
//BUCLE VORAZ
let objetos = [];
let j = pesoMaximo;
for (let i=pesos.length-1; i>0; i--){
numIter++;
if (values[i][j] !== values[i-1][j] &&
values[i][j] === values[i-1][j-pesos[i]] + valores[i]){
objetos.push(i);
j -= pesos[i];
}
}
return objetos;El peso máximo de la mochila es j=8. El voraz itera desde el último objeto i=4 hasta el i=1 observando la columna j=8. Si esa posición en la fila i es igual que la anterior i-1 se ignora, que en el código detectamos cuando values[i][j] !== values[i-1][j]. Por eso no se marca el 70 que está en la posición (i, j) = (4, 8). La que está en (i, j)=(3, 8) se marca si además ese valor 70 es igual que el valor de la fila anterior en la columna j-pesos[i], es decir, en la columna 8-5=3 que tiene el valor 40, más el valor del objeto de esa fila 30, en total 70. En ese caso agregamos el objeto i=3 a la mochila y le restamos el peso del objeto al valor máximo 8, quedando j=3, columna donde iteramos a continuación.
Hacemos otra iteración empezando en (i, j)=(2, 3), viendo que el valor en esa posición es distinto del anterior en esa columna (0). Y también viendo que j-pesos[i] nos da cero (3-pesos[2]=3-3=0), valor cero que sumado al valor del objeto de esa fila 40 resulta igual que la posición (i, j)=(2, 3) que estamos considerando. Agregamos el objeto i=2 a la mochila y restamos peso quedando j=0, con lo que finalizamos el bucle for en la siguiente iteración.
Finalmente tenemos en la solución el array [3, 2], que son los índices (contando desde cero) de los objetos que presentamos en el ejemplo interactivo como {i: 3, p: 5, v: 30}, {i: 2, p: 3, v: 40}, con un peso total de 8 y un valor total de 70.
El coste del algoritmo para llenar la mochila
No perdemos generalidad si consideramos que los arrays se inician en uno en lugar de cero. El problema se establece sobre n objetos para llenar una mochila con peso máximo P. La primera parte del algoritmo tiene por objeto rellenar la tabla de resultados intermedios. Para ello creamos el array vacío values cuya longitud es P+1. Luego iteramos por el bucle doble i=1..n × j=1..P. Entonces el coste de esta parte es Max(P+1, n×P) = n×P, puesto que asintóticamente n×P es mayor que P+1. En resumen el coste de esta parte es O(nP). La segunda parte ejecuta el bucle voraz i=n..1, por lo que el coste final es el mismo O(nP)
Una consideración con este algoritmo es que sólo sirve para pesos y peso máximo enteros. Si tuviéramos que trabajar con pesos no enteros para una mochila de 8 kilos, tendríamos que limitar los pesos de los objetos a un número de decimales. Si los limitamos a tres estaremos hablando de pesos y peso máximo en gramos en lugar de kilogramos. Pasaríamos los datos a gramos y tendríamos que llenar una mochila con peso máximo de P = 8000 gramos. Como el coste es proporcional al peso de la mochila, esto encarece enormemente el coste.