Generar nuevos grafos 1
Generar nuevos grafos

Podemos a acceder al asistente de generación en la aplicación Grafos SVG con el botón . Ahí encontraremos las operaciones en grafos que vimos en el tema anterior. Y la generación de nuevos grafos que veremos en este tema.
Se exponen grafos simples rejilla, círculo, cíclico, completo, bipartito, puesta sol, rueda y estrella.
En el siguiente tema veremos como generar nuevos grafos avanzados como Kneser, Johnson, Petersen, circulante, platónico, sudoku y otros.
Hay muchísimas más clases de grafos, pero al menos estos servirán de entrada al conocimiento de algunos de ellos.
Nuevo grafo rejilla
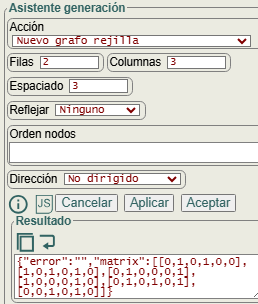
El nuevo grafo rejilla crea un grafo en una rejilla visual de filas por columnas con el panel que se observa en la Figura. En un grafo rejilla m × n todas las aristas pueden disponerse en forma de rejilla con m filas y n columnas.
Los parámetros espaciado, reflejar y orden nodos pueden configurarse para modificar el aspecto visual del grafo generado. Con dirección se configura grafo no dirigido, dirigido arriba, dirigido abajo y todo dirigido.
En todos las operaciones y nuevos grafos del asistente generación encontramos el icono que es un enlace a un tema que lo explica, como a este apartado para este caso. Y el botón nos da acceso al código JavaScript de la función que genera el grafo.
En todos los casos se ofrece el resultado con un objeto con el posible error y la matriz de adyacencia resultante.
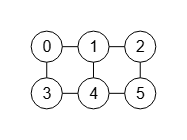
En la Figura vemos el nuevo grafo no dirigido obtenido para una rejilla de 2×3. El espaciado entre dos nodos tiene un valor de 3 unidades, contándose desde el centro del círculo de un nodo al siguiente, siendo la unidad el radio del nodo.
La función JavaScript que genera el grafo rejilla y que expondremos después es generateGridGraph({rows=0, columns=0, direction="none"}), donde los parámetros espaciado, reflejar y orden nodos no se incluyen, pues son ajustes visuales que se aplican después de obtener la matriz de adyacencia con la función generateGridGraph(), posicionando los nodos según esos ajustes.
0 1 0 1 0 0 1 0 1 0 1 0 0 1 0 0 0 1 1 0 0 0 1 0 0 1 0 1 0 1 0 0 1 0 1 0
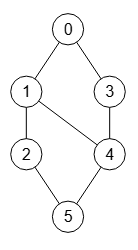
Si importamos en la aplicación la matriz de adyacencia obtenida, vemos en la Figura el grafo obtenido, que no deja de ser un grafo rejilla aunque visualmente no lo parece. La aplicación toma esa matriz de adyacencia y le aplica el ajuste visual ajustar a rejilla que ya vimos en un tema anterior. A ese ajuste le pasamos los parámetros espaciado y orden nodos.
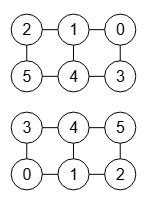
Después se aplica otro ajuste visual para reflejar el grafo si el valor es horizontal o vertical, cuyos resultados son los que se muestran en la Figura respectivamente.
Observe que podríamos no reflejar el grafo y pasar el orden de nodos 2,1,0,5,4,3 para obtener el primero de ellos y 3,4,5,0,1,2 para obtener el segundo. Cualquiera de estos ajustes visuales no modificará la matriz de adyacencia.
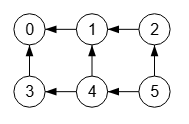
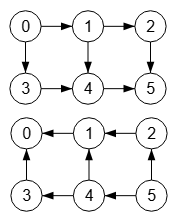
Se modificará la matriz de adyacencia si pasamos el parámetro dirección como por ejemplo dirigido arriba, con el resultado que se muestra en la Figura. Recordemos que con una arista i 🡒 j si i>j entonces la arista es dirigida arriba. Si la mitad o más de las aristas son así entonces el grafo es dirigido arriba. En este caso todas las aristas son dirigidas arriba.
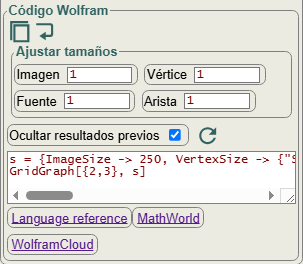
La aplicación nos ofrece también el código para ejecutar en Wolfram Cloud como se observa en la Figura. También ofrece enlaces a la documentación en Wolfram.
Es posible ajustar tamaños de salida en Wolfram para la imagen, vértices, texto y grosor de las aristas.
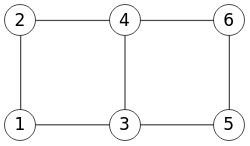
El resultado de la ejecución en Wolfram se expone en la Figura. La disposición de los nodos es distinta (vertical) a la que obtuvimos en nuestra aplicación (horizontal) en la Figura. Recordemos, además, que en Wolfram los nodos se enumeran desde 1 mientras que la aplicación lo hace desde 0.
En el código siguiente usamos la función GridGraph[], encontrando más información en la página Grid Graph de Wolfram Math World.
Acompañamos la declaración s = {ImageSize->250, VertexSize ... } que viene a ser un estilo similar para la presentación visual de nodos y aristas similar a los de nuestra aplicación.
s = {ImageSize->250, VertexSize->{"Scaled", 0.13}, VertexLabels ->Placed["Name", Center], VertexLabelStyle->Directive[Black, 17.5],
VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}};
GridGraph[{2,3},s]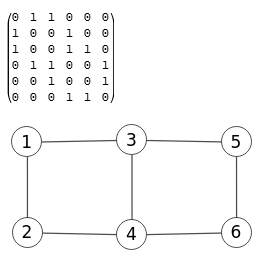
Si al código Wolfram anterior agregamos las siguientes líneas:
m = AdjacencyMatrix[%]; MatrixForm[m] AdjacencyGraph[m, s]
obtenemos la matriz de adyacencia y grafo que vemos en la Figura. Es el mismo grafo que el de la Figura, pero Wolfram dispone gráficamente los nodos opuestos verticalmente, diríamos que hace una reflexión vertical del grafo.
0 1 1 0 0 0 1 0 0 1 0 0 1 0 0 1 1 0 0 1 1 0 0 1 0 0 1 0 0 1 0 0 0 1 1 0
Podemos comprobar que la matriz de adyacencia anterior se corresponde con la permutación 0,3,1,4,2,5 del grafo de inicio de la Figura, así como el de la Figura, que era la presentación gráfica obtenida directamente desde la matriz de adyacencia. Así que el grafo de Wolfram y el que obtenemos en nuestra aplicación son isomorfos.
Comparemos los dos grafos dirigido abajo y dirigido arriba de la Figura generados en la aplicación. El código que se genera para ejecutar en Wolfram se expone a continuación, donde combinamos ambas generaciones y ponemos los comentarios en Wolfram (* Directed down *) y (* Directed up *).
En Wolfram no existe el concepto de direccionalidad en grafos, tal como la entendemos dirigidos arriba y abajo. Puede hacerse uso de la función ReverseGraph[g] que cambia la dirección de todas las aristas, como vemos en el código siguiente.
s = {ImageSize->250, VertexSize->{"Scaled", 0.13}, VertexLabels ->Placed["Name", Center],
VertexLabelStyle->Directive[Black, 17.5],
VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}};
(* Directed down *)
GridGraph[{2,3}, DirectedEdges->True, s]
(* Directed up *)
ReverseGraph[GridGraph[{2,3}, DirectedEdges->True, s]]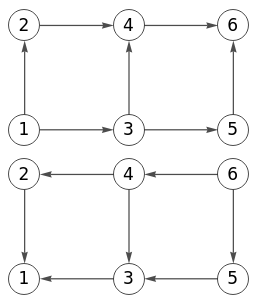
En la Figura vemos el resultado del código anterior, con el dirigido abajo y el dirigido arriba manteniendo la direccionalidad con el mismo criterio que usamos en la aplicación, aunque la disposición de los nodos es vertical y no horizontal, como ya vimos antes.
Por último veamos el código JavaScript para ejecutar generateGridGraph(), donde el argumento direction puede ser none, undirected, directed-up, directed-down para crear el grafo sin ninguna arista, no dirigido, dirigido arriba y dirigido abajo respectivamente.
function generateGridGraph({rows=0, columns=0, direction="none"}){
let dev = {error: "", matrix: []}, temp;
try {
let nodeNumber = rows * columns;
dev.matrix = Array.from({length: nodeNumber}, () =>
Array.from({length: nodeNumber}, () => 0));
if (direction!=="none"){
let arr = Array.from({length: rows}, () =>
Array.from({length: columns}, () => []));
for (let i=0; i<rows; i++) {
for (let j=1; j<columns; j++) {
arr[i][j].push(i * columns + j-1);
}
}
for (let j=0; j<columns; j++) {
for (let i=1; i<rows; i++) {
arr[i][j].push((i-1) * columns + j);
}
}
for (let i=0; i<arr.length; i++) {
for (let j=0; j<arr[i].length; j++) {
let index1 = i * columns + j;
for (let k=0; k<arr[i][j].length; k++) {
let index2 = arr[i][j][k];
if (["undirected", "directed-up"].includes(direction))
dev.matrix[index1][index2] = 1;
if (["undirected", "directed-down"].includes(direction))
dev.matrix[index2][index1] = 1;
}
}
}
}
} catch(e){dev.error = `#Error generateGridGraph(): ${clean(e.message)}`}
return dev;
}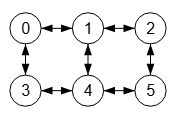
La función generateGridGraph no permite la dirección todo dirigido (directed-all), pero la aplicación si se ofrece esa posibilidad. En la Figura vemos el resultado. Si recordamos en un tema anterior sobre arista toda dirigida o arista doble, no es posible representar con la matriz de adyacencia un grafo todo dirigido, pues se corresponde con uno no dirigido. Sin embargo, tras obtener la matriz de adyacencia, la aplicación fuerza aristas dobles o todas dirigidas actuando sobre el JSON más que sobre la matriz de adyacencia.
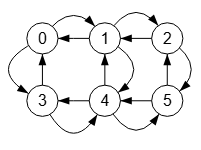
En la Figura hemos separado todas las aristas para observar que son aristas dobles.
Nuevo grafo círculo
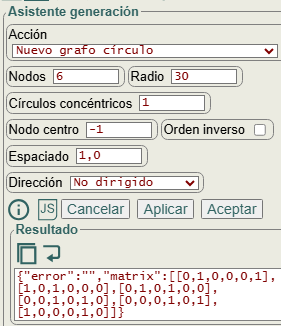
En el asistente de generación podemos crear un nuevo grafo círculo, como se observa en la Figura. Un grafo círculo es el que todas sus aristas se conforman en una disposición circular. Las opciones nodos y dirección afectan a la matriz de adyacencia y son los argumentos de la función JavaScript generateCircleGraph({n=0, direction="none"}) que genera el grafo círculo.
Las otras opciones radio, nodo centro, orden inverso y espaciado se aplican como ajustes visuales después de ejecutar la función generateCircleGraph(), no afectando a la matriz de adyacencia.
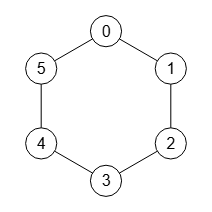
En la Figura vemos el grafo círculo no dirigido con 6 nodos, aplicando un radio 30. La disposición en un círculo usa la funcionalidad ajustar a círculo que ya vimos en un tema anterior, traspasándose las opciones radio, nodo centro, orden inverso y espaciado para ejecutar en ese ajuste a círculo.
0 1 0 0 0 1 1 0 1 0 0 0 0 1 0 1 0 0 0 0 1 0 1 0 0 0 0 1 0 1 1 0 0 0 1 0
La matriz de adyacencia de todos los grafos círculo no dirigidos tiene todos "1" en las diagonales junto a la diagonal principal, con "1" también en las esquinas superior derecha e inferior izquierda.
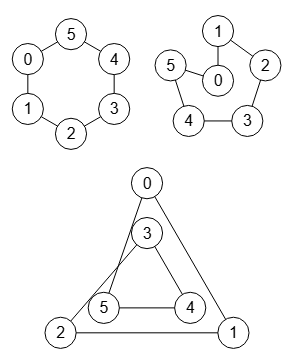
En la Figura vemos varias opciones visuales. La primera es con orden inverso activado. La segunda es poniendo como nodo centro al nodo 0. La tercera es poniendo 2 círculos concentricos. El espaciado, que por defecto tiene valor 1, separa los nodos radialmente en esa cantidad cuando hay círculos concéntricos.
Cualquiera de estos ajustes visuales no modificará la matriz de adyacencia.
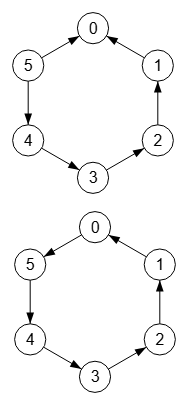
Un grafo círculo no es necesariamente un grafo cíclico que veremos en el siguiente apartado y que se genera con generateCyclicGraph({n=0, direction="none"}). Solo son iguales si son no dirigidos. En la Figura vemos un grafo círculo y otro cíclico, ambos dirigidos arriba. Vea que el grafo círculo no completa un ciclo.
0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 1 0 0 0 1 0Grafo cíclico
0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0
Las matrices de adyacencia son prácticamente iguales, a excepción de la arista 5 🡒 0 en el grafo círculo y 0 🡒 5 en el cíclico.
Vea que ambos son dirigido arriba, pues la mayor parte de las aristas van de un nodo origen con mayor índice que el de destino, como hemos explicado en el tema direccionalidad de grafos.
En Wolfram no existe una función que genere un grafo círculo. Solo hay CycleGraph para generar un grafo cíclico, que también se explica en Cycle Graph en Wolfram MathWorld. Existe la opción Graph Layout que podemos aplicar a un grafo para indicar que disposición de nodos usar. Así con GraphLayout->"CircularEmbedding" se disponen los nodos sobre un círculo. En la aplicación usaremos CycleGraph[n] que, con no dirigidos, es igual que nuestra función como explicamos más arriba.
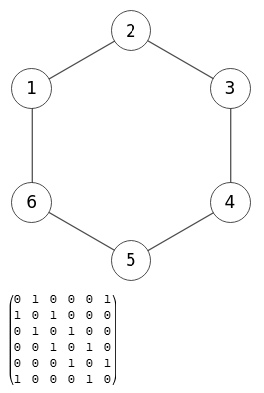
En Figura vemos un grafo círculo no dirigido que puede construirse con CycleGraph[6, s] en Wolfram, siendo s una declaración de estilo para asemejarlo visualmente a nuestro grafo.
0 1 0 0 0 1 1 0 1 0 0 0 0 1 0 1 0 0 0 0 1 0 1 0 0 0 0 1 0 1 1 0 0 0 1 0
Observe que la matriz de adyacencia es la misma que obtuvimos en la aplicación.
s = {ImageSize->250, VertexSize->{"Scaled", 0.13}, VertexLabels ->Placed["Name", Center],
VertexLabelStyle->Directive[Black, 17.5],
VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}};
CycleGraph[6, s]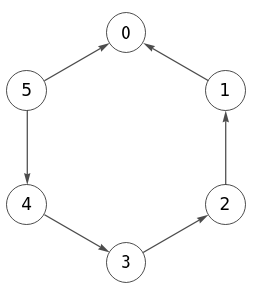
Para un grafo círculo dirigido no tenemos una función específica en Wolfram como ya hemos comentado. Pero podemos exportar nuestro grafo círculo dirigido arriba que obtuvimos más arriba, en el primer grafo de la Figura. En Figura puede ver que las flechas coinciden. El código de exportación a Wolfram es el siguiente, donde siempre se fuerzan las etiquetas de los nodos para hacerlas coincidir con las del grafo de la aplicación.
g = AdjacencyGraph[{{0,0,0,0,0,0},{1,0,0,0,0,0},{0,1,0,0,0,0},{0,0,1,0,0,0},{0,0,0,1,0,0},{1,0,0,0,1,0}},
ImageSize->250, VertexSize->{"Scaled", 0.13}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center],
3->Placed[2,Center], 4->Placed[3,Center], 5->Placed[4,Center], 6->Placed[5,Center]},
VertexLabelStyle->Directive[Black, 17.5], VertexStyle->White,
DirectedEdges->True, EdgeStyle->{{Black,Thickness[0.005]}}]El código JavaScript para generar un grafo círculo es el siguiente, donde el argumento direction puede ser none, undirected, directed-up, directed-down para crear el grafo sin ninguna arista, no dirigido, dirigido arriba y dirigido abajo respectivamente. La opción todo dirigido se aplica posteriormente a la ejecución de esta función, de la misma forma que explicamos más arriba.
function generateCircleGraph({n=0, direction="none"}) {
let dev = {error: "", matrix: []}, temp;
try {
dev.matrix = Array.from({length: n}, () => Array.from({length: n}, () => 0));
if (direction!=="none") {
for (let i=n-1; i>0; i--) {
if (["undirected", "directed-up"].includes(direction))
dev.matrix[i][i-1] = 1;
if (["undirected", "directed-down"].includes(direction))
dev.matrix[i-1][i] = 1;
}
if (["undirected", "directed-up"].includes(direction))
dev.matrix[n-1][0] = 1;
if (["undirected", "directed-down"].includes(direction))
dev.matrix[0][n-1] = 1;
}
} catch(e){dev.error = `#Error generateCircleGraph(): ${clean(e.message)}`}
return dev;
}Nuevo grafo cíclico
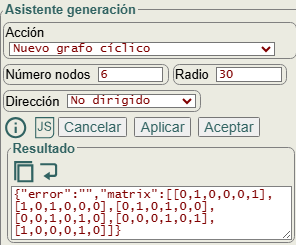
En el asistente de generación podemos generar un grafo cíclico. En un grafo cíclico todas sus aristas conforman un ciclo. Como se observa en la Figura las opciones número nodos y dirección se traspasan a la función function generateCyclicGraph({n=0, direction="none"}). La opción radio sirve para un ajuste visual a círculo, no modificando la matriz de adyacencia que se obtiene con dicha función.
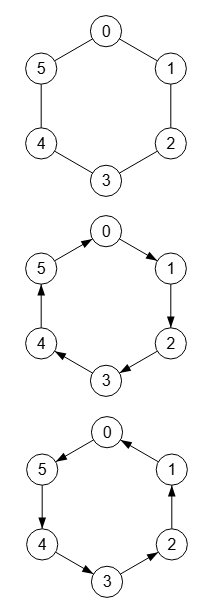
En la Figura vemos un grafo cíclico no dirigido, dirigido abajo y dirigido arriba con 6 nodos, con estas matrices de adyacencia:
0 1 0 0 0 1 1 0 1 0 0 0 0 1 0 1 0 0 0 0 1 0 1 0 0 0 0 1 0 1 1 0 0 0 1 0Dirigido abajo
0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 1 0 0 0 0 0Dirigido arriba
0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0
En el apartado anterior comentamos la diferencia entre un grafo círculo y cíclico que se produce sólo para los dirigidos.
Recordemos que dirigido abajo significa que la mayor parte de las aristas van desde un nodo con menor índice a uno con mayor índice, como sucede con todas las del grafo dirigido menos la arista 5🡒0, que es dirigida arriba necesaria para cerrar el ciclo. Y dirigido arriba es lo contrario. Ver más en direccionalidad de grafos.
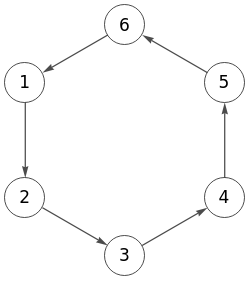
El grafo cíclico en Wolfram puede obtenerse con la función CycleGraph[n], a lo que agregamos la dirección y el estilo con CycleGraph[6, DirectedEdges->True, s] para este ejemplo. En la Figura se observa que obtenemos el mismo grafo dirigido abajo que con la aplicación, a diferencia de que los nodos se inician en 1 en Wolfram y en 0 en la aplicación.

Podemos obtener la matriz de adyacencia en Wolfram si agregamos MatrixForm[AdjacencyMatrix[%]] al código que se expone a continuación. Se observa que es la misma matriz para el dirigido abajo obtenido en nuestra aplicación.
s = {ImageSize->250, VertexSize->{"Scaled", 0.13}, VertexLabels ->Placed["Name", Center],
VertexLabelStyle->Directive[Black, 17.5],
VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}};
CycleGraph[6, DirectedEdges->True, s]El concepto de direccionalidad que define grafos dirigidos arriba y abajo no existe en Wolfram. Si no se especifican explícitamente las aristas en Wolfram y se genera un nuevo grafo con algo como CycleGraph[6, DirectedEdges->True], siempre se entenderá como dirigido abajo, es decir, con aristas que van de un nodo con menor índice que el de destino, excluyendo aquellas aristas que se precisen con otra dirección, como "6🡒1" que cierra el ciclo en la Figura.
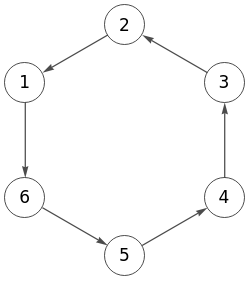
Para conseguir forzarlo dirigido arriba podemos aplicar ReverseGraph[g], como hacemos para el de la Figura (ver también este párrafo en el tema anterior sobre direccionalidad en grafos).

La matriz de adyacencia es como la que obtuvimos en la aplicación para el dirigido arriba.
s = {ImageSize->250, VertexSize->{"Scaled", 0.13}, VertexLabels ->Placed["Name", Center],
VertexLabelStyle->Directive[Black, 17.5],
VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}};
ReverseGraph[CycleGraph[6, DirectedEdges->True, s]]El código JavaScript para generar un grafo cíclico es el siguiente, donde el argumento direction puede ser none, undirected, directed-up, directed-down para crear el grafo sin ninguna arista, no dirigido, dirigido arriba y dirigido abajo respectivamente. La opción todo dirigido se aplica posteriormente a la ejecución de esta función, de la misma forma que explicamos más arriba.
function generateCyclicGraph({n=0, direction="none"}) {
let dev = {error: "", matrix: []}, temp;
try {
dev.matrix = Array.from({length: n}, () => Array.from({length: n}, () => 0));
if (direction!=="none") {
for (let i=n-1; i>0; i--) {
if (["undirected", "directed-up"].includes(direction))
dev.matrix[i][i-1] = 1;
if (["undirected", "directed-down"].includes(direction))
dev.matrix[i-1][i] = 1;
}
if (["undirected", "directed-up"].includes(direction))
dev.matrix[0][n-1] = 1;
if (["undirected", "directed-down"].includes(direction))
dev.matrix[n-1][0] = 1;
}
} catch(e){dev.error = `#Error generateCyclicGraph(): ${clean(e.message)}`}
return dev;
}Nuevo grafo completo
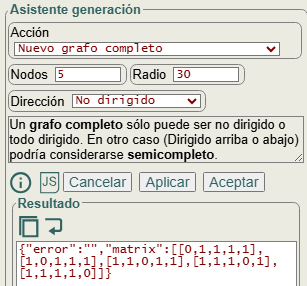
En el asistente de generación podemos generar un grafo completo, que es aquel que tiene aristas entre todos los nodos. Como se observa en la Figura las opciones nodos y dirección se traspasan a la función function generateCompleteGraph({n=0, direction="none"}). La opción radio sirve para un ajuste visual a círculo, no modificando la matriz de adyacencia que se obtiene con dicha función.
Un grafo completo es no dirigido (arista i-j) o todo dirigido (arista i🡘j) , no pudiendo ser grafo completo los dirigidos arriba (arista i🡒j) o abajo (arista j🡒i), puesto que en estos dos casos no se cumple que haya aristas en el sentido contrario. En la aplicación lo advertimos con el texto Un grafo completo sólo puede ser no dirigido o todo dirigido, en otro caso (dirigido arriba o abajo) podrían considerarse semicompleto
. Más abajo explicaremos más sobre esto.
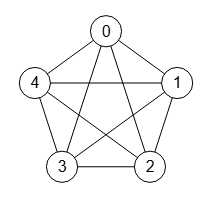
En la Figura vemos un grafo completo no dirigido con 5 nodos, donde hay aristas entre todos los nodos.
0 1 1 1 1 1 0 1 1 1 1 1 0 1 1 1 1 1 0 1 1 1 1 1 0
Su matriz de adyacencia tiene 1 en todas las posiciones menos en la diagonal.
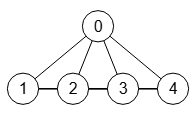
Si importamos la matriz de adyacencia anterior que devuelve generateCompleteGraph({n:5}), obtenemos la disposición que vemos en la Figura, donde todos los nodos a partir del segundo se ubican en el mismo nivel, superponiéndose las aristas. La mejor forma de presentar un grafo completo es disponer los nodos sobre un círculo, por eso la aplicación utiliza a continuación el ajuste visual a círculo, pasándole la opción radio, obteniéndose el resultado de la Figura.
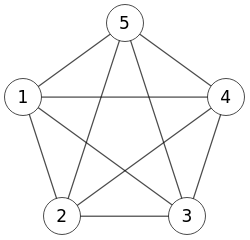
La función CompleteGraph[n] genera un grafo completo en Wolfram Cloud, con más información en Complete Graph de Wolfram MathWorld.
En la aplicación pasamos el estilo s del grafo con CompleteGraph[5, s], con la finalidad de asimilar el estilo de nodos y aristas con el grafo obtenido en la aplicación. Vea que en Wolfram los nodos se enumeran desde 1 y en la aplicación desde 0.
s = {ImageSize->250, VertexSize->{"Scaled", 0.13}, VertexLabels ->Placed["Name", Center],
VertexLabelStyle->Directive[Black, 17.5],
VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}};
CompleteGraph[5, s]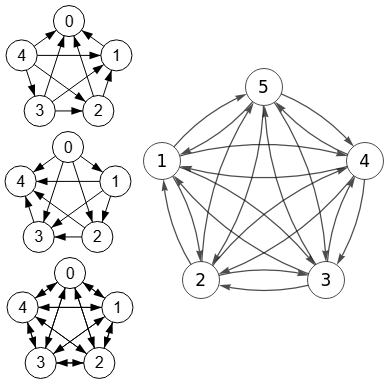
En la Figura se observa grafos generados con 5 nodos. Los tres de la izquierda generados en la aplicación son dirigido arriba, dirigido abajo y todo dirigido. A la derecha está la presentación en Wolfram, que se consigue con CompleteGraph[5, DirectedEdges->True, s], presentando los tres de la misma forma todo dirigido, pues no parece que se contemple la posibilidad de aristas en un sólo sentido, pues podría contradecir la definición de grafo completo que dice Un grafo completo tiene aristas entre todos los nodos
.
Por lo tanto aunque la aplicación puede generar un grafo como completo con aristas en un sólo sentido (dirigido arriba o abajo), realmente no son grafos completos por definición. Podríamos denominarlos semicompletos, pues hay una arista al menos parcial entre todos los nodos. Veremos más en el siguiente apartado al explicar la función isGraphComplete().
s = {ImageSize->250, VertexSize->{"Scaled", 0.13}, VertexLabels ->Placed["Name", Center],
VertexLabelStyle->Directive[Black, 17.5],
VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}};
CompleteGraph[5, DirectedEdges->True, s]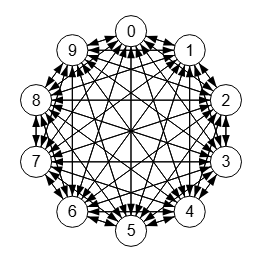
En la Figura se observa un grafo completo con 10 nodos y todas las aristas dobles o todo dirigido.
El código JavaScript para generar un grafo completo es el siguiente, donde el argumento direction puede ser none, undirected, directed-up, directed-down para crear el grafo sin ninguna arista, no dirigido, dirigido arriba y dirigido abajo respectivamente. La opción todo dirigido se aplica posteriormente a la ejecución de esta función, de la misma forma que explicamos más arriba.
function generateCompleteGraph({n=0, direction="none"}) {
let dev = {error: "", matrix: []}, temp;
try {
dev.matrix = Array.from({length: n}, () => Array.from({length: n}, () => 0));
if (direction!=="none") {
for (let i=0; i<n; i++) {
for (let j=0; j<i; j++) {
if (i!==j) {
if (["undirected", "directed-up"].includes(direction))
dev.matrix[i][j] = 1;
if (["undirected", "directed-down"].includes(direction))
dev.matrix[j][i] = 1;
}
}
}
}
} catch(e){dev.error = `#Error generateCompleteGraph(): ${clean(e.message)}`}
return dev;
}Es el grafo completo isGraphComplete()
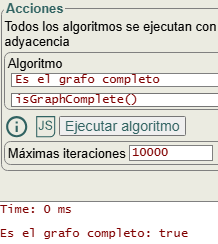
En la sección de algoritmos podemos encontrar la función isGraphComplete({matrix}) que, pasándole la matriz de adyacencia, nos chequea si el grafo es o no completo. El código JavaScript siguiente comprueba que hay aristas entre todos los nodos.
function isGraphComplete({matrix=[]}){
let result = false;
try {
result = matrix.every((v, i) => v.every((w, j) => i===j && w===0 || i!==j && w!==0));
} catch(e){result = e.message}
return result;
}
En la Figura vemos un grafo completo con 20 nodos, cuya acción del algoritmo isGraphComplete() resultará verdadero.
Este es el JSON de ese grafo, que hemos generado con lo visto antes como un nuevo grafo completo y, a continuación modificamos las propiedades en la configuración nodeValueAuto y nodeRadius. También hemos simplificado los padres al exportar el JSON, que incluirá arrays de índices en los "parent" para que el JSON ocupe menos espacio.
{"nodes":[
{"index":0,"nodeOffset":"2.5","parent":-1},
{"index":1,"nodeOffset":"59.86 -23.04","parent":0},
{"index":2,"nodeOffset":"66.01 -17.36","parent":[0,1]},
{"index":3,"nodeOffset":"69.86 -8.51","parent":[0,1,2]},
{"index":4,"nodeOffset":"70.54 2.64","parent":[0,1,2,3]},
{"index":5,"nodeOffset":"67.5 15","parent":[0,1,2,3,4]},
{"index":6,"nodeOffset":"60.54 27.36","parent":[0,1,2,3,4,5]},
{"index":7,"nodeOffset":"49.86 38.51","parent":[0,1,2,3,4,5,6]},
{"index":8,"nodeOffset":"36.01 47.36","parent":[0,1,2,3,4,5,6,7]},
{"index":9,"nodeOffset":"19.86 53.04","parent":[0,1,2,3,4,5,6,7,8]},
{"index":10,"nodeOffset":"2.5 55","parent":[0,1,2,3,4,5,6,7,8,9]},
{"index":11,"nodeOffset":"-14.86 53.04","parent":[0,1,2,3,4,5,6,7,8,9,10]},
{"index":12,"nodeOffset":"-31.01 47.36","parent":[0,1,2,3,4,5,6,7,8,9,10,11]},
{"index":13,"nodeOffset":"-44.86 38.51","parent":[0,1,2,3,4,5,6,7,8,9,10,11,12]},
{"index":14,"nodeOffset":"-55.54 27.36","parent":[0,1,2,3,4,5,6,7,8,9,10,11,12,13]},
{"index":15,"nodeOffset":"-62.5 15","parent":[0,1,2,3,4,5,6,7,8,9,10,11,12,13,14]},
{"index":16,"nodeOffset":"-65.54 2.64","parent":[0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]},
{"index":17,"nodeOffset":"-64.86 -8.51","parent":[0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]},
{"index":18,"nodeOffset":"-61.01 -17.36","parent":[0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17]},
{"index":19,"nodeOffset":"-54.86 -23.04","parent":[0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18]}
],
"config":{
"nodeValueAuto":"none",
"nodeRadius":2
}}Incluimos en la configuración "nodeRadius":2 para reducir el radio de los nodos. Además incluimos "nodeValueAuto":"none" para imponer los valores automáticos de los nodos con el valor "none" para ningún texto.
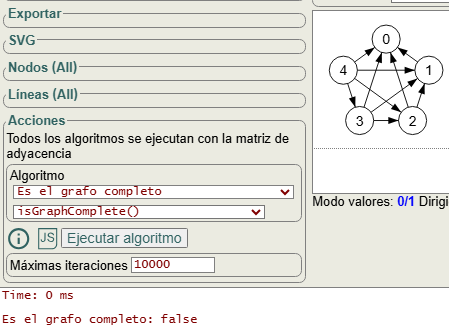
Si en la aplicación generamos un grafo completo con 5 nodos (Figura) dirigido arriba, podemos comprobar que realmente no es un grafo completo, pues no hay aristas entre todos los nodos. Por ejemplo, existe la arista "4🡒0" pero no existe la arista "0🡒4". Ya vimos estos grafos en la Figura, donde se comprobaba que para Wolfram todo grafo completo dirigido debe tener todas las aristas dobles o todo dirigidas.
Nuevo grafo bipartito
En un grafo bipartito podemos agrupar los nodos en dos subconjuntos disjuntos de tal forma que desde un nodo en un subconjunto salen aristas exclusivamente a nodos del otro subconjunto. Cuando esas aristas van a todos los nodos del otro subconjunto, diremos que se trata de un grafo bipartito completo.
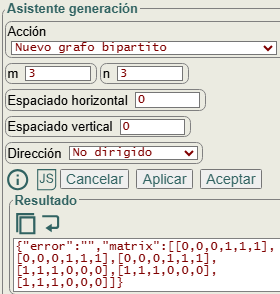
En la Figura vemos la parte que genera un grafo bipartito en la sección del asistente de generación en la aplicación.
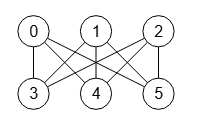
Al generar grafo bipartito completo de m=3, n=3 obtenemos la siguiente matriz de adyacencia:
0 0 0 1 1 1 0 0 0 1 1 1 0 0 0 1 1 1 1 1 1 0 0 0 1 1 1 0 0 0 1 1 1 0 0 0
Se observa que el cuadrante de la mitad superior derecha e inferior izquierda son todos unos. Si importa la anterior matriz de adyacencia observará que se muestra exactamente como vemos en la Figura, pues la ubicación automática por niveles es apta para presentar un grafo bipartito sin más modificaciones. En cualquier caso en la aplicación podemos modificar el espaciado tanto horizontal como vertical de los nodos. Estos ajustes visuales no modifican la matriz de adyacencia y son aplicados posteriormente a su obtención.

En la Figura vemos el grafo bipartito completo en Wolfram con la disposición vertical de los nodos, enumerándose los nodos desde 1 como es usual en Wolfram. Se obtiene con CompleteGraph[{m, n}]. Recordemos que en el apartado anterior usábamos la misma función CompleteGraph[n] con un único argumento n para obtener un grafo completo, siendo la misma función, pues con un argumento se obtiene un grafo completo con n nodos y con dos argumentos se obtiene uno bipartito completo. Con k argumentos se obtendría un k-bipartito, pero esto no se contempla en nuestra aplicación. Hay más información en Complete Bipartite Graph y en Bipartite Graph de Wolfram MathWorld.
El código para generar el grafo anterior en Wolfram Cloud es el siguiente:
s = {ImageSize->250, VertexSize->{"Scaled", 0.13}, VertexLabels ->Placed["Name", Center],
VertexLabelStyle->Directive[Black, 17.5],
VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}};
CompleteGraph[{3,3}, s]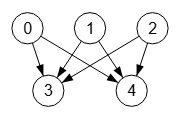
En la Figura vemos un grafo bipartito m=3, n=2 y con la opción dirigido abajo, donde las aristas van de un nodo con menor índice a uno con mayor índice.
0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0
En la matriz de adyacencia vemos en el cuadrante superior derecha las dos columnas y tres filas de "1", con las flechas que arrancan desde el cuadrante inferior izquierdo.
Un grafo bipartito dirigido no puede ser además completo, pues no se cumple el principio de que cada nodo en un subconjunto tenga aristas a todos los nodos del otro subconjunto. Por ejemplo, vemos la arista 2🡒4 pero no existe la arista contraria 4🡒2.

En la Figura vemos como Wolfram presenta ese grafo bipartito dirigido abajo, cuyo código es el que se expone a continuación.
s = {ImageSize->250, VertexSize->{"Scaled", 0.13}, VertexLabels ->Placed["Name", Center],
VertexLabelStyle->Directive[Black, 17.5],
VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}};
CompleteGraph[{3,2}, DirectedEdges->True, s]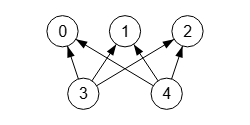
En la Figura vemos el grafo bipartito dirigido arriba.

Y en la Figura vemos como Wolfram presenta ese grafo bipartito dirigido arriba, cuyo código es el que se expone a continuación, haciendo uso de ReverseGraph[g]. Pues como hemos comentado en temas anteriores, en Wolfram no encuentro una forma de aplicar directamente la direccionalidad en grafos tal como la contemplo en la aplicación.
s = {ImageSize->250, VertexSize->{"Scaled", 0.13}, VertexLabels ->Placed["Name", Center],
VertexLabelStyle->Directive[Black, 17.5],
VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}};
ReverseGraph[CompleteGraph[{3,2}, DirectedEdges->True, s]]Dijimos antes que un grafo bipartito dirigido no puede ser completo. Pero si en el ejemplo de grafo bipartito completo de la Figura, que es por tanto no dirigido, eliminamos una o más aristas, el grafo seguirá siendo bipartito pero ya no será completo. La función generateBipartiteGraph() genera siempre un grafo bipartito completo, con aristas de cada nodo en un subconjunto a todos los nodos del otro subconjunto.
function generateBipartiteGraph({m=0, n=0, direction="none"}) {
let dev = {error: "", matrix: []}, temp;
try {
let p = m+n;
dev.matrix = Array.from({length: p}, () => Array.from({length: p}, () => 0));
if (direction!=="none") {
for (let i=0; i<p; i++) {
for (let j=i; j<p; j++){
if ((i<m && j>=m)||(i>=m && j<m)) {
if (["undirected", "directed-up"].includes(direction))
dev.matrix[j][i] = 1;
if (["undirected", "directed-down"].includes(direction))
dev.matrix[i][j] = 1;
}
}
}
}
} catch(e){dev.error = `#Error generateBipartiteGraph(): ${clean(e.message)}`}
return dev;
}Es el grafo bipartito isGraphBipartite()
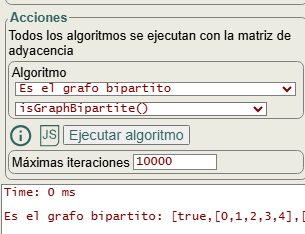
En la Figura vemos la sección de acciones donde podemos ejecutar el algoritmo isGraphBipartite({matrix}), recibiendo una matriz de adyacencia y devolviendo el resultado. Usa el algoritmo getColoringGreedy({matrix}) para colorear los nodos del grafo y que aún no he publicado en este sitio, pero que haré previsiblemente en el futuro.
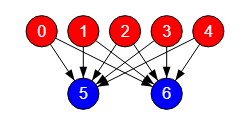
Usando como ejemplo el bipartito generado con m=5, n=2 dirigido abajo, como expusimos en el apartado anterior nuevo grafo bipartito, vemos en la Figura el grafo generado, tras ejecutar el algoritmo de coloreado getColoringGreedy({matrix}) que asigna los colores en dos subconjuntos disjuntos. Como no hay aristas entre los nodos de cada subconjunto, entonces es un grafo bipartito pues se pueden separar los nodos en esos dos subconjuntos disjuntos.
La ejecución del algoritmo isGraphBipartite({matrix}) devuelve el array [true, [0,1,2,3,4], [5,6]], donde la primera posición nos dice que es bipartito, en cuyo caso las dos siguientes son las listas de nodos en cada subconjunto disjunto. La aplicación además incluye texto explicativo y el tiempo de ejecución, que es insignificante en este ejemplo:
Time: 0 ms
Es el grafo bipartito: [true,[0,1,2,3,4],[5,6]]
El grafo es bipartito con sus aristas agrupadas en dos conjuntos disjuntos de nodos con valores siguientes:
U = 0, 1, 2, 3, 4
V = 5, 6
Un multigrafo con autobucles no puede ser bipartito, pues el autobucle no cumple claramente la definición ...desde un nodo en un subconjunto salen aristas exclusivamente a nodos del otro subconjunto
que vimos al principio del apartado anterior. Por eso en el algoritmo excluimos los multigrafos que se chequean con es multigrafo isMultiGraph() que expusimos en un tema anterior.
Como dijimos, se ejecuta el coloreado del grafo con getColoringGreedy({matrix}) que, para el ejemplo anterior, devuelve el array [1,1,1,1,1,2,2], donde cada número representa un color en una lista de colores y cada posición es el índice del nodo en el grafo. Convertimos ese array en un conjunto con new Set(coloring) y obtenemos el conjunto {1, 2}, contando que tiene 2 elementos (colores) deducimos entonces que el grafo es bipartito.
function isGraphBipartite({matrix=[]}) {
let result = [false, [], []];
try {
let multigraph = isMultiGraph({matrix});
if (typeof multigraph==="string") throw new Error(multigraph);
if (!multigraph) {
let coloring = getColoringGreedy({matrix});
if (typeof coloring==="string") throw new Error(coloring);
if ((new Set(coloring)).size===2) {
result[0] = true;
let arr = coloring.map((v, i) => [i, v]);
result[1] = arr.filter(v => v[1]===1).map(v => v[0]);
result[2] = arr.filter(v => v[1]===2).map(v => v[0]);
}
}
} catch(e){result = e.message}
return result;
}En Wolfram puede comprobar si un grafo es bipartito con la función BipartiteGraphQ.
Es el grafo bipartito completo isGraphBipartiteComplete()
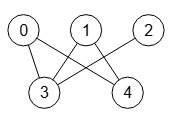
El grafo de la Figura es bipartito, pues de cada nodo en el subconjunto de la primera fila salen aristas exclusivamente a uno o más nodos del subconjunto de la segunda fila. Pero no es completo, pues no todos los nodos tienen aristas con el resto de nodos del otro subconjunto, observando que es lo que sucede con la arista faltante "2-4".
Podemos comprobar si un grafo es bipartito completo con el algoritmo isGraphBipartiteComplete({matrix}), devolviendo el array [false, [0,1,2], [3,4]], con el valor falso indicando que no es completo, agregando dos arrays incluyendo los índices de nodos en cada subconjunto, lo que indica que es bipartito. Si tampoco fuera bipartito, esos dos arrays aparecerían vacíos.
Time: 0 ms Es el grafo bipartito completo: [false,[0,1,2],[3,4]]
function isGraphBipartiteComplete({matrix=[]}) {
let result = [false, [], []];
try {
let res = isGraphBipartite({matrix});
if (typeof res==="string") throw new Error(res);
let [ok, set1, set2] = res;
if (ok) {
result = [false, set1, set2];
for (let i=0; i<set1.length; i++) {
for (let j=0; j<set2.length; j++) {
let [ii, jj] = [set1[i], set2[j]];
if (!(matrix[ii][jj]!==0 && matrix[jj][ii]!==0)){
ok = false;
break;
}
}
if (!ok) break;
}
result[0] = ok;
}
} catch(e){result = e.message}
return result;
}No he encontrado una función en Wolfram para ejecutar esto.
Nuevo grafo corona
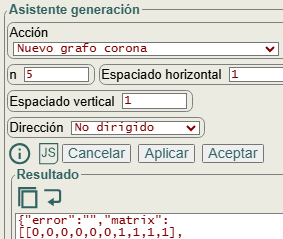
El grafo corona de dimensión n es el que tiene como nodos los índices de los subconjuntos Ni = {u0, u1, ..., un-1} y Nj = {v0, v1, ..., vn-1} siendo todas las aristas de forma [ui, vj] para 0 ≤ i ≤ n-1 y 0 ≤ j ≤ n-1 con i ≠ j.
La arista [ui, vj] es no dirigida ui - vj en general, pero en la aplicación también cabe toda dirigida ui 🡘 vj o dirigida ui 🡒 vj para los casos dirigida arriba o abajo.
Los conjuntos de nodos Ni y Nj pueden ser cualesquiera, pero si partimos del conjunto de índices M = {0, 1, 2, ..., n-1} de tamaño n, la definición se convierte en Ni = {0, 1, ..., n-1} y Nj = {n, n+1, ..., 2n-1} siendo todas las aristas de forma [i, j] para 0 ≤ i ≤ n-1 y n ≤ j ≤ 2n-1 con j ≠ n+i. En base a esta definición plantearemos el algoritmo en JavaScript que veremos más abajo.

En la Figura vemos un grafo corona con n=5.
0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 1 0 1 1 1 0 0 0 0 0 1 1 0 1 1 0 0 0 0 0 1 1 1 0 1 0 0 0 0 0 1 1 1 1 0 0 1 1 1 1 0 0 0 0 0 1 0 1 1 1 0 0 0 0 0 1 1 0 1 1 0 0 0 0 0 1 1 1 0 1 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0
La matriz de adyacencia del grafo corona tiene "1" en los cuadrantes superior derecha e inferior izquierda menos en las subdiagonales de esos cuadrantes.

En la Figura vemos un grafo bipartito con m=5, n=5, observando que es como el corona anterior pero sin las aristas verticales.
0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0
La matriz de adyacencia del grafo bipartitio m=5, n=5 no tiene subdiagonales en los cuadrantes.
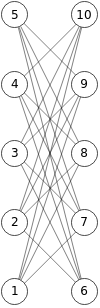
El grafo corona con n=5 en Wolfram Cloud se observa en la Figura, donde vemos la disposición vertical en lugar de la horizontal de la Figura, además de que los índices se enumeran desde 1 en lugar de 0.
El código para esa ejecución se expone a continuación, donde resaltamos en color azul las dimensiones que hemos aplicado para que la imagen no sea excesivamente grande, como explicaremos después. Se puede actuar sobre unos controles para ajustar tamaños de imagen (0.4), vértices (0.7), textos (0.7) y grueso de aristas (1.5) como factores sobre la unidad. O simplemente modificar los valores numéricos en el código.
Usamos GraphData[{"Crown", n}]] y Graph[] para agregar el estilo en la variable "s". Puede ver más información del grafo corona en Wolfram MathWorld.
s = {ImageSize->100, VertexSize->{"Scaled", 0.091}, VertexLabels ->Placed["Name", Center],
VertexLabelStyle->Directive[Black, 12.25], VertexStyle->White, EdgeStyle->{{Black,Thickness[0.0075]}}};
Graph[GraphData[{"Crown", 5}], s]
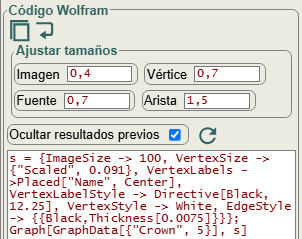
Por defecto exportamos los nuevos grafos a Wolfram con un tamaño de imagen de 250 (imageSize). En la mayor parte de los casos las dimensiones de los nodos en VertexSize, tamaño texto en VertexLabelStyle y EdgeLabelStyle y grueso de aristas en EdgesStyle son proporcionales a ese tamaño y se ajustan en Wolfram más o menos como en nuestra aplicación. Pero en otros casos no sucede así.
Podemos ajustar tamaños con los controles que se observan en la Figura, factores que por defecto tienen valor 1, incrementándose o decrementándose proporcionalmente para valores mayores o menores que 1 respectivamente. Para este ejemplo hemos tenido que aplicar factores 0.4 (250×0.4 = 100) para reducir tamaño de la imagen, 0.7 para el tamaño de textos y 1.5 para el grueso de aristas, valores que iremos probando hasta conseguir el efecto deseado. En cualquier caso también puede modificar directamente esos valores en el código.
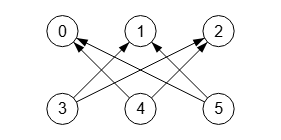
El grafo corona también puede ser dirigido, como este de la Figura con n=3 dirigido arriba. Wolfram no admite grafos coronas dirigidos, pues si agregamos DirectedEdges en el código Graph[GraphData[{"Crown", 3}], DirectedEdges->True] será ignorado.
El código JavaScript para ejecutar generateCrownGraph() es como el siguiente:
function generateCrownGraph({n=0, direction="none"}) {
let dev = {error: "", matrix: []}, temp;
try {
let m = 2*n;
dev.matrix = Array.from({length: m}, () => Array.from({length: m}, () => 0));
if (direction!=="none") {
for (let i=0; i<m; i++) {
for (let j=i; j<m; j++){
if (j!==n+i && (i<n && j>=n|| i>=n && j<n)) {
if (["undirected", "directed-up"].includes(direction))
dev.matrix[j][i] = 1;
if (["undirected", "directed-down"].includes(direction))
dev.matrix[i][j] = 1;
}
}
}
}
} catch(e){dev.error = `#Error generateCrownGraph(): ${clean(e.message)}`}
return dev;
}Nuevo grafo puesta sol
Un grafo puesta sol (sunlet graph) con n nodos es un grafo cíclico del que cuelgan otros n nodos, así que en total tendrá 2n nodos.
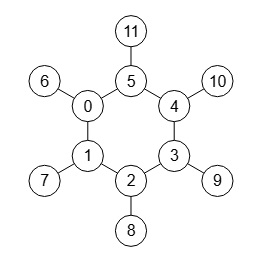
En la Figura puede ver un grafo Puesta sol con 6 nodos en el círculo interior y otros 6 nodos que cuelgan de ellos.
0 1 0 0 0 1 1 0 0 0 0 0 1 0 1 0 0 0 0 1 0 0 0 0 0 1 0 1 0 0 0 0 1 0 0 0 0 0 1 0 1 0 0 0 0 1 0 0 0 0 0 1 0 1 0 0 0 0 1 0 1 0 0 0 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0
Esta es la matriz de adyacencia obtenida del grafo anterior, observando las diagonales con "1" que caracterizan este grafo. Como en casos anteriores, si importa directamente esta matriz no se obtiene el resultado de la Figura, pues se aplica el ajuste visual ajustar a círculo, pasando la opción radio 20, como vemos en la Figura y, además, imponiendo 2 círculos concéntricos y orden inverso.
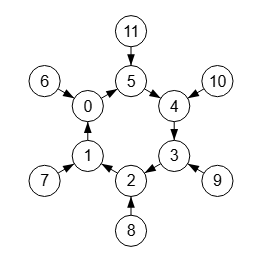
Si lo hacemos dirigido arriba, como el de la Figura, podemos ver el caracter cíclico del grafo interno. Es dirigido arriba pues, a excepción de la arista "0🡒5" que cierra el ciclo del círculo interior, el resto de los nodos, que es la mayor parte, apuntan a otro con índice menor.
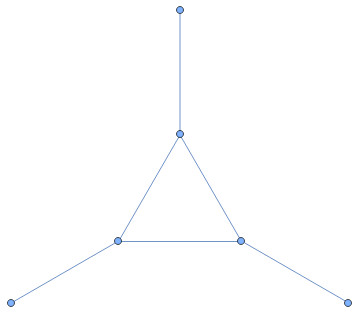
Para presentarlo en Wolfram supuestamente deberíamos usar GraphData["Sunlet", 6]. Sin embargo no consigo que funcione, por lo que pongo el comentario (* Doesn't work "Sunlet" only "NetGraph" *), funcionando solo con GraphData["NetGraph"], que presenta un Puesta de sol de 3 nodos, como se observa en la Figura, pues tal como dice en esta página de Sunlet Graph de Wolfram Math World, The 3-sunlet graph is also known as the net graph
(El grafo puesta de sol de 3 nodos es también conocido como grafo red).
GraphData["Sunlet", 6] (* Doesn't work "Sunlet" only "NetGraph" *) GraphData["NetGraph"]
El código para generar el grafo puesta de sol es generateSunletGraph():
function generateSunletGraph({n=0, direction="none"}) {
let dev = {error: "", matrix: []}, temp;
try {
dev.matrix = Array.from({length: n}, () => Array.from({length: n}, () => 0));
if (direction!=="none") {
for (let i=n-1; i>0; i--) {
if (["undirected", "directed-up"].includes(direction))
dev.matrix[i][i-1] = 1;
if (["undirected", "directed-down"].includes(direction))
dev.matrix[i-1][i] = 1;
}
if (["undirected", "directed-up"].includes(direction))
dev.matrix[0][n-1] = 1;
if (["undirected", "directed-down"].includes(direction))
dev.matrix[n-1][0] = 1;
for (let i=0; i<n; i++) {
let row = Array.from({length:n}, (v, j) => {
if (i===j) {
return direction!=="none" ? 1: 0;
} else {
return 0;
}
});
dev.matrix[i].push(...row);
}
let arr = Array.from({length: n}, () => 0);
for (let i=0; i<n; i++){
let row = Array.from({length:n}, (v, j) => {
if (i===j) {
return direction!=="none" ? 1: 0;
} else {
return 0;
}
});
row.push(...arr);
dev.matrix.push(row);
}
for (let i=0; i<2*n; i++) {
for (let j=n; j<2*n; j++) {
if (direction==="directed-up"){
dev.matrix[i][j] = 0;
} else if (direction==="directed-down") {
dev.matrix[j][i] = 0;
}
}
}
}
} catch(e){dev.error = `#Error generateSunletGraph(): ${clean(e.message)}`}
return dev;
}Nuevo grafo rueda
Un grafo rueda (wheel graph) de n nodos es un grafo cíclico de n-1 nodos conectados a un nodo central. En la Figura vemos como crearlo en el asistente de generación.
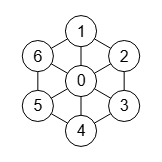
En la Figura vemos un nodo rueda de 7 nodos, con 6 de ellos formando un ciclo en el círculo externo y con todos sus nodos conectados al nodo 0.
0 1 1 1 1 1 1 1 0 1 0 0 0 1 1 1 0 1 0 0 0 1 0 1 0 1 0 0 1 0 0 1 0 1 0 1 0 0 0 1 0 1 1 1 0 0 0 1 0
Esta es la matriz de adyacencia obtenida, a la cual se aplica el ajuste visual ajustar a círculo, pasando la opción radio 20, como vemos en la Figura y, además, imponiendo nodo centro el nodo 0.
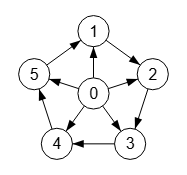
En la Figura vemos un grafo rueda de 6 nodos dirigido abajo, pues a excepción de "5🡒1", todas las aristas van desde un nodo con menor índice que el de destino. Se observa en el subgrafo del círculo externo que es cíclico, pues la arista "5🡒1" cierra el ciclo.
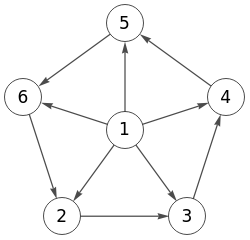
En Wolfram se presenta el grafo rueda dirigido anterior como se observa en la Figura. A excepción de la enumeración de índices y del sentido de giro de las flechas en el círculo externo, son equivalentes. Utiliza la función WheelGraph[n], encontrando más información en Wheel Graph de Wolfram MathWorld. A continuación se muestra el código que genera la aplicación para ejecutar en Wolfram Cloud.
s = {ImageSize->250, VertexSize->{"Scaled", 0.13}, VertexLabels ->Placed["Name", Center],
VertexLabelStyle->Directive[Black, 17.5],
VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}};
WheelGraph[6, DirectedEdges->True, s]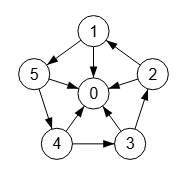
En la Figura vemos un grafo rueda de 6 nodos dirigido arriba.
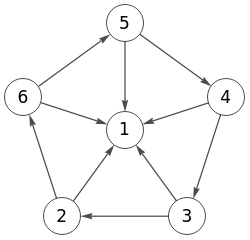
Y su traslado a Wolfram en Figura haciendo uso de ReverseGraph[g] que cambia la dirección de todas las aristas.
s = {ImageSize->250, VertexSize->{"Scaled", 0.13}, VertexLabels ->Placed["Name", Center],
VertexLabelStyle->Directive[Black, 17.5],
VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}};
ReverseGraph[WheelGraph[6, DirectedEdges->True, s]]El código JavaScript para generar el grafo rueda es generateWheelGraph() que se muestra a continuación:
function generateWheelGraph({n=0, direction="none"}) {
let dev = {error: "", matrix: []}, temp;
try {
dev.matrix = Array.from({length: n}, () => Array.from({length: n}, () => 0));
if (direction!=="none") {
for (let i=n-1; i>0; i--) {
if (["undirected", "directed-up"].includes(direction)) dev.matrix[i][i-1] = 1;
if (["undirected", "directed-down"].includes(direction)) dev.matrix[i-1][i] = 1;
}
if (["undirected", "directed-up"].includes(direction)) dev.matrix[1][n-1] = 1;
if (["undirected", "directed-down"].includes(direction)) dev.matrix[n-1][1] = 1;
for (let i=2; i<n; i++) {
if (["undirected", "directed-up"].includes(direction)) dev.matrix[i][0] = 1;
if (["undirected", "directed-down"].includes(direction)) dev.matrix[0][i] = 1;
}
}
} catch(e){dev.error = `#Error generateWheelGraph(): ${clean(e.message)}`}
return dev;
}Nuevo grafo estrella
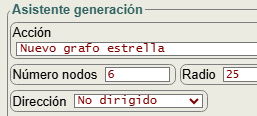
Un grafo estrella (star graph) de n nodos es un grafo con un nodo central y n-1 nodos que conectan única y exclusivamente con ese nodo central. El nodo central tiene, entonces, grado n-1 y el resto grado 1.
En la Figura vemos como generar un grafo estrella en el asistente generación. Las opciones número de nodos y dirección se pasan como argumentos a la función generateStarGraph({n=0, direction="none"}) que devuelve una matriz de adyacencia, a la que a continuación se le aplicará un ajuste visual para ajustar a círculo con el nodo 0 en en el centro, pasando la opción radio del círculo.
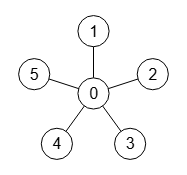
En la Figura vemos un grafo estrella de 6 nodos no dirigido.
0 1 1 1 1 1 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0
La matriz de adyacencia de los grafos estrella no dirigidos tiene unos en la primera fila y primera columna, sin contar con el 0 de la esquina superior izquierda sobre la diagonal.
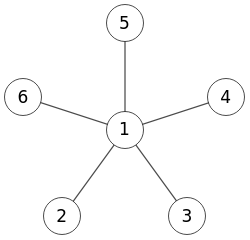
En la Figura vemos como se presenta en Wolfram usando la función StarGraph[n] con más información en Star Graph. Aparte de la numeración de nodos, es igual que el obtenido en la aplicación.
s = {ImageSize->250, VertexSize->{"Scaled", 0.13}, VertexLabels ->Placed["Name", Center],
VertexLabelStyle->Directive[Black, 17.5],
VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}};
StarGraph[6, s]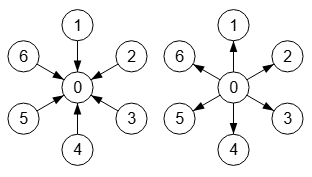
En la Figura vemos grafos estrella dirigido arriba y abajo.
0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0Dirigido abajo
0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Sus matrices de adyacencia tienen unos en la primera columna o en la primera fila, respectivamente.
A continuación vemos el código para presentarlos en Wolfram, con StarGraph[7, DirectedEdges->True, s] para el dirigido abajo y con ReverseGraph[StarGraph[7, DirectedEdges->True, s]] para el dirigido arriba, usando ReverseGraph[g].
s = {ImageSize->250, VertexSize->{"Scaled", 0.13}, VertexLabels ->Placed["Name", Center],
VertexLabelStyle->Directive[Black, 17.5],
VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}};
(* Directed up *)
ReverseGraph[StarGraph[7, DirectedEdges->True, s]]
(* Directed down *)
StarGraph[7, DirectedEdges->True, s]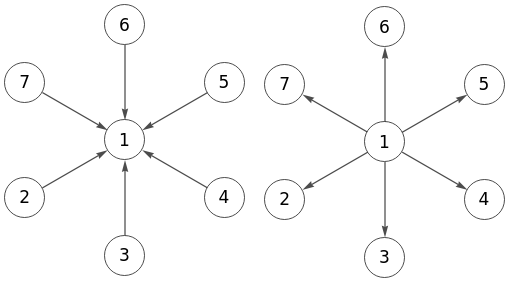
El código JavaScript para ejecutar generateStarGraph() es el siguiente:
function generateStarGraph({n=0, direction="none"}) {
let dev = {error: "", matrix: []}, temp;
try {
dev.matrix = Array.from({length: n}, () => Array.from({length: n}, () => 0));
for (let i=1; i<n; i++) {
if (["undirected", "directed-up"].includes(direction)) dev.matrix[i][0] = 1;
if (["undirected", "directed-down"].includes(direction)) dev.matrix[0][i] = 1;
}
} catch(e){dev.error = `#Error generateStarGraph(): ${clean(e.message)}`}
return dev;
}