Planificaciones
Planificación de tareas
Los algoritmos voraces sirven para resolver los problemas de planificación de tareas. Una es la planificación con plazo fijo que veremos en un siguiente apartado. Ahora veremos las planificaciones de minimización del tiempo en el sistema.
El problema se basa en minimizar el tiempo que invierte cada tarea en el sistema. Supongamos que un servidor tiene que atender n tareas, cada una con un tiempo ti requerido para completarse. Las tareas están en una cola esperando ser atendidas. El servidor podría atenderlas en orden de llegada. O bien podría periódicamente planificar en que orden las atiende.
Supongamos que la cola tuviese tres tareas con tiempos requeridos 4, 6, 2 unidades de tiempo. El servidor las ejecutará en ese orden. El primer cliente no tiene que esperar para ser servido, completándose su servicio en 4 unidades de tiempo. El segundo esperará 4 unidades mientras se sirve al primero, completándose en 4+6=10 unidades. El último lo hará en 4+6+2=12 unidades. El total de tiempos de espera es de 4+10+12=26 unidades de tiempo ¿Cuál es el orden de ejecución que produce el menor tiempo total de espera? La respuesta es hacer las 3! = 6 permutaciones posibles y comprobarlo:
| Orden ejecución | Tiempo total |
|---|---|
| 1, 2, 3 | 4 + (4+6) + (4+6+2) = 24 |
| 1, 3, 2 | 4 + (4+2) + (4+2+6) = 22 |
| 2, 1, 3 | 6 + (6+4) + (6+4+2) = 28 |
| 2, 3, 1 | 6 + (6+2) + (6+2+4) = 26 |
| 3, 1, 2 | 2 + (2+4) + (2+4+6) = 20 |
| 3, 2, 1 | 2 + (2+6) + (2+6+4) = 22 |
Es la permutación que ordena por tiempos crecientes 2, 4, 6 la que consigue minimizar el tiempo total de espera. Entonces la solución es muy simple, ordenamos el array inicial de tiempos de tareas [4, 6, 2] en orden creciente, ejecutándose las tareas con el orden [2, 4, 6]. Y no es necesario implementar nada más.
¿Y entonces qué tiene que ver el algoritmo voraz con este problema? Recordemos la estructura básica:
function voraz(conjunto){
let resultado = crear(conjunto);
while (!esSolucion(resultado) && !esVacio(conjunto)){
let candidato = seleccionar(conjunto);
if (esCompletable(resultado, candidato)) {
resultado = guardar(resultado, candidato);
}
}
return resultado;
}El conjunto es el array de tiempos requeridos, ya ordenados por tiempos crecientes. El resultado será otro array con las tareas en el orden que se ejecutarán. El bucle while se sustituye por un for que itere por el conjunto. Todas las tareas formarán parte del resultado, con lo que todas las tareas se seleccionan. Y también todas las tareas completan el resultado, dado que ya fueron ordenadas previamente. En resumen, el voraz es trivial, es decir, no es necesario implementarlo una vez se ordenen las tareas. Aunque trivial, el agoritmo voraz está claramente ímplicito en la solución del problema.
Como con todo problema donde se aplique el algoritmo voraz, hay que analizar la optimalidad y el coste. El coste es obviamente el de ordenar un array O(n log n). Para explicar por qué ordenando por tiempos obtenemos una solución óptima usaremos un esquema gráfico.
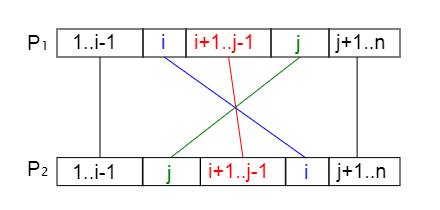
En la Figura la planificación P1 es la óptima. La longitud de los segmentos horizontales representa tiempo de ejecución. Se ejecutan n tareas. El bloque 1..i-1 representa la ejecución de la tarea 1 hasta la i-1. De igual forma se indican los bloques i+1..j-1 y j+1..n. Intercambiamos dos tareas i y j, la primera con un tiempo de ejecución inferior a la segunda. La planificación resultante P2 no será optima, puesto que aunque los bloques 1..i-1 y j+1..n se ejecutan con los mismos tiempos de espera, el tiempo de espera del bloque i+1..j-1 empeora. Vease que se desplaza a la derecha. Por lo tanto el tiempo de espera total de esta planificación no mejora la anterior.
Planificación de tareas con plazo fijo
El problema de la planificación con plazo fijo se basa en que tenemos un número de tareas, donde cada tarea se ejecuta en una unidad de tiempo y tiene un beneficio si se lleva a cabo antes de un plazo máximo. Se trata de seleccionar aquellas tareas que se ejecuten no después de sus plazos máximos y con el objetivo final de maximizar el beneficio.
Ejemplo: Planificación con plazo fijo
planificar(tareas): Supongamos que tenemos estas tareas donde cada una se representa con un objeto:
tareas = [
{num: 1, beneficio: 7, plazo: 3},
{num: 2, beneficio: 10, plazo: 1},
{num: 3, beneficio: 20, plazo: 3},
{num: 4, beneficio: 5, plazo: 1},
{num: 5, beneficio: 15, plazo: 1},
{num: 6, beneficio: 3, plazo: 3}
]La primera idea es ordenarlas por beneficio dado que esta característica es la clave para maximizar el valor:
tareas = [
{num: 3, beneficio: 20, plazo: 3},
{num: 5, beneficio: 15, plazo: 1},
{num: 2, beneficio: 10, plazo: 1},
{num: 1, beneficio: 7, plazo: 3},
{num: 4, beneficio: 5, plazo: 1},
{num: 6, beneficio: 3, plazo: 3}
]Como cada tarea se ejecuta en una unidad de tiempo y no hay tareas que se puedan ejecutar después de 3 unidades de tiempo (3 es el máximo de los plazos), es evidente que la planificación contendrá como máximo 3 tareas. Para realizar la planificación iremos iterando las tareas de la lista anterior, seleccionando siempre la primera:
| Número tarea | Beneficio | Plazo | Instante | Plazo≥Instante |
|---|---|---|---|---|
| 3 | 20 | 3 | 1 | 3≥1⇒Sí |
Tomemos la segunda tarea con número 5. Su plazo es 1 y por lo tanto sólo puede ejecutarse en primer lugar. Desplazamos la tarea anterior (puesto que su plazo es 3 y aún cabe ejecutarse) para dejar un hueco donde insertar la que estamos considerando:
| Número tarea | Beneficio | Plazo | Instante | Plazo≥Instante |
|---|---|---|---|---|
| 5 | 15 | 1 | 1 | 1≥1⇒Sí |
| 3 | 20 | 3 | 2 | 3≥2⇒Sí |
Consideramos la siguiente tarea con número 2. Su plazo es 1 y el único sitio donde su plazo es menor o igual que el instante sería sustituirla por la número 5, desechando ésta. Pero la tarea 5 tiene mayor beneficio y no debe sustituirse. Así que desechamos la tarea 2.
Veamos la siguiente tarea con número 1. Su plazo es 3 y estamos en el instante 3, así que es perfectamente ejecutable en este instante. La seleccionamos agregándola al final de la lista:
| Número tarea | Beneficio | Plazo | Instante | Plazo≥Instante |
|---|---|---|---|---|
| 5 | 15 | 1 | 1 | 1≥1⇒Sí |
| 3 | 20 | 3 | 2 | 3≥2⇒Sí |
| 1 | 7 | 3 | 3 | 3≥3⇒Sí |
Ya tenemos tres tareas. Las siguientes dos últimas tareas podrían sustituir a las anteriores, pero no ejecutarse a continuación pues estaríamos en el instante 4 que supera sus plazos 1 y 3. Pero no pueden sustituir a las anteriores porque su beneficio es menor. Se desechan entonces. Finalizamos con la selección 5, 3, 1 con beneficio total 42.
El algoritmo para implementar la planficación con plazo fijo es el siguiente:
function planificar(tareas=[{num: 0, beneficio: 0, plazo: 0}]){
//numIter++;
tareas = tareas.sort((a,b) => b.beneficio-a.beneficio);
let plazos = [0, ...tareas.map(v => v.plazo)];
let resultado = plazos.map(v => 0);
let numTareas = 1;
resultado[1] = 1;
for (let i=2; i<=tareas.length; i++){
//numIter++;
let tarea = numTareas;
while (plazos[resultado[tarea]] > Math.max(plazos[i], tarea)){
//numIter++;
tarea--;
}
if (plazos[i] > tarea){
for (let j=numTareas; j>=tarea+1; j--){
//numIter++;
resultado[j+1] = resultado[j];
}
resultado[tarea+1] = i;
numTareas++;
}
}
resultado = resultado.filter(v => v>0);
return resultado;
}En la entrada del algoritmo ordenamos las tareas por orden decreciente de beneficio. Declaramos un array de plazos y otro que almacenará el resultado. Ambos array tienen una posición inicial en el índice cero que servirá a modo de centinela para el control en los bucles siguientes. Guardamos la primera tarea en el resultado y ejecutamos un bucle que itera desde la segunda hasta la última tarea. Este es el bucle voraz, donde la función de selección está implícita en la ordenación de las tareas.
Todas las tareas son seleccionadas por el voraz y dentro del bucle comprabaremos si la tarea es completable. Esto lo llevamos a cabo con el bucle while que observa entre las que ya forman parte del resultado si la que estamos considerando cabe en la ejecución. En ese caso la insertamos en el resultado desplazando, en su caso, las necesarias a la derecha del array.
Finalizamos quitando posibles huecos que hayan quedado en el array, incluso la primera posición que usamos como centinela. Para ello usamos el método filter.
La demostración de optimalidad es algo extensa para exponerla aquí. Se expone en la referencia Fundamentos de Algoritmia de G.Brassard, P.Bratley ya comentada en un tema anterior.
Analicemos el coste del algoritmo. El peor caso sucederá cuando la ordenación decreciente por beneficio coincide con la de plazos. Por ejemplo, con las siguientes tareas 70,7; 60,6; 50,5; 40,4; 30,3; 20,2; 10,1
tareas = [
{num: 1, beneficio: 70, plazo: 7},
{num: 2, beneficio: 60, plazo: 6},
{num: 3, beneficio: 50, plazo: 5},
{num: 4, beneficio: 40, plazo: 4},
{num: 5, beneficio: 30, plazo: 3},
{num: 6, beneficio: 20, plazo: 2},
{num: 7, beneficio: 10, plazo: 1}
]Una vez ordenadas por beneficio decreciente se observa que también quedan ordenadas por plazo decreciente. Todas las tareas caben en la planificación y cada vez que se analiza la tarea i para ver si es completable en el bucle while itera por todas las i-1 que ya forman parte del resultado. Luego para insertarla en el resultado desplaza i veces. Si ignoramos por el momento el coste de los métodos de ordenar tareas y crear arrays de plazos y resultado, así como el filtrado final del array del resultado, podemos considerar un coste unitario a la entrada de la función y también en cada inicio de cada bucle. Esto se implementa en el código con la sentencia numIter++ que va contando las iteraciones. En el caso peor se comprueba que el coste calculado del contador de iteraciones es exactamente el siguiente:
Para el ejemplo dado el coste calculado es T(7) = 72 = 49. Si ahora tenemos en cuenta el coste de la ordenación y creación de arrays, sabemos que la ordenación tiene un coste asintótico O(n log n). La creación de arrays y filtrado tendrá un coste O(n) cada una. Así que con todas esas sentencias en secuencia por fuera del bucle voraz, el coste final es el máximo de ellos O(n log n). El coste del bucle voraz ∑i=2..n (2i-1) = n2-1 domina sobre el anterior, siendo el coste asintótico final O(n2). Podemos reducir este coste usando una estructura de partición que tiene esencialmente un coste lineal.
Estructura de partición o de conjuntos disjuntos
Tenemos n elementos numerados como 0, 1, 2, ..., n-1. Hemos de ubicarlos en conjuntos disjuntos, de tal forma que un elemento se encuentre en cada momento en un único conjunto. En cada conjunto selecionamos el más pequeño como rótulo de ese conjunto. Es evidente que habrán como mucho n conjuntos disjuntos. Por lo tanto podríamos disponer de un array de rótulos también de tamaño n, donde cada posición almacenará el rótulo del conjunto al que pertenece el elemento.
A continuación presentamos un ejemplo interactivo y luego pasaremos a explicar esta estructura. Una estructura de partición o de conjuntos disjuntos queda completamente definida por un array de rótulos y un array de rangos (cuyo cometido explicaremos después). En este ejemplo verá que presentamos otras cosas para documentar el ejemplo, como arrays que representan los estados inicial o actual de los conjuntos, una lista de elementos y otro que representa los árboles actuales. Pero estos objetos no forman parte de la estructura de partición.
Ejemplo: Estructura de partición
Conjuntos iniciales: Elementos: Rótulos: Rangos: Conjuntos actuales: Árboles actuales: Supongamos que inicialmente tenemos los elementos 0, 1, 2, 3, 4. Se podrían ubicar inicialmente en 5 conjuntos disjuntos { 0 }, { 1 }, { 2 }, { 3 }, { 4 }. El array de rótulos será R=[0, 1, 2, 3, 4], donde el valor coincide con la posición en el array, es decir, si se cumple que R[i] = i entonces ese elemento i-ésimo es el rótulo de ese conjunto. En otro caso si R[i] = j con i≠j entonces el elemento i se encuentra en el conjunto con rótulo j.
Supongamos ahora que tenemos una operación para fusionar los dos primeros conjuntos quedando { 0, 1 }, { 2 }, { 3 }, { 4 }. El array de rótulos será R=[0, 0, 2, 3, 4]. Vemos que R[0]=0 entonces el elemento 0 es el rótulo. Y que R[1]=0 entonces el elemento 1 está en el conjunto con rótulo 0. Implementar esta operación es, en principio, muy fácil. Supongamos que tenemos dos conjuntos con rótulos i, j, cumpliéndose que R[i]=i y que R[j]=j por ser ambos rótulos. Para fusionarlos podríamos, en principio, detectar el rótulo de menor valor, por ejemplo i<j, con lo que haríamos R[j] ← i asignando el rótulo más grande al más pequeño. Vease que así la operación fusionar tiene un coste unitario de una simple comparación más asignación. Podríamos implementar la fusión de conjuntos con rótulos a y b con este código:
if (a<b){
rotulos[b] = a;
} else{
rotulos[a] = b;
}Con esta estructura definir una función para buscar en que conjunto está un elemento i es simple. Iteramos extrayendo j ← R[i]. Si j=i entonces es un rótulo y el elemento se encuentra en el conjunto con rótulo i. En otro caso si j≠i entonces extraemos k ← R[j]. Si k=j entonces el rótulo es j, sino seguimos repitiendo el proceso hasta llegar a un caso donde sean iguales. Esto se podría implementar con un simple bucle como el siguiente que devolverá el rótulo del conjunto donde se encuentre el elemento a buscar:
while (rotulos[elemento]!==elemento){
elemento = rotulos[elemento];
}Esto podría tener un coste peor igual al número de elementos cuando el árbol asociado se degenere en una lista de nodos.
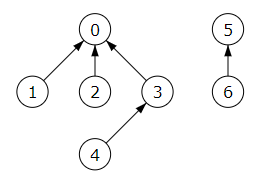
Una estructura de conjuntos disjuntos es, en el fondo, una estructura de árboles. Por ejemplo, en la Figura podemos ver la que se representa con el array de rótulos [0, 0, 0, 0, 3, 5, 5], con dos conjuntos disjuntos de distinta altura. El árbol del rótulo 0 tiene altura 2 mientras que el del rótulo 5 tiene altura 1. La altura se mide desde el primer nodo, de tal forma que un nodo raíz sin hijos tiene altura 0.
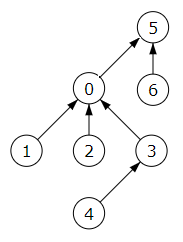
Si el propósito fuera fusionar estos dos conjuntos, anexaríamos el conjunto con rótulo de menor valor (el 0) al de mayor valor (el 5), tal como se muestra en la Figura. Esto supone que la altura final sea 3, habiéndose incrementado la altura en esta operación. El array de rótulos ahora es [5, 0, 0, 0, 3, 5, 5].
El incremento de altura empeora el coste en las operaciones de búsqueda, que tal como vimos antes, en el peor caso requiere iterar por una rama hasta alcanzar el rótulo raíz del árbol. Vease el camino que hemos de recorrer si buscáramos el elemento 4.
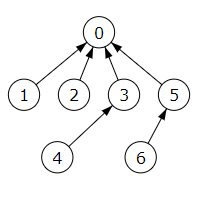
Entonces la solución pasa por anexar siempre el árbol de menor altura al de mayor altura, como se observa en la Figura. El árbol resultante tiene altura 2, no incrementándose la altura final. El array de rótulos es ahora [0, 0, 0, 0, 3, 0, 5]. Para implementar esto podríamos ir guardando las alturas de los árboles y consultarlas para fusionar según este dato.
Dispondremos inicialmente de un array de rangos donde almacenaremos esas alturas. Luego explicaremos la razón de denominarlo "rangos" en lugar de "alturas". Con esto la implementación final de la operación para fusionar dos rótulos sería la del siguiente código. Si ambos son de igual altura seguimos el criterio de anexar el menor valor de rótulo al de mayor valor, creciendo en altura el de menor valor (con lo que no se incrementa la altura final). En otro caso anexamos el de menor altura al de mayor altura independientemente de los valores de los rótulos.
function fusionar(rotulos=[], rangos=[], rotulo1=0, rotulo2=0){
let a = Math.min(rotulo1, rotulo2);
let b = Math.max(rotulo1, rotulo2);
if (rangos[a]===rangos[b]){
rotulos[b] = a;
rangos[a]++;
} else if (rangos[a]>rangos[b]){
rotulos[b] = a;
} else {
rotulos[a] = b;
}
return [rotulos, rangos];
}Aún queda una optimización más que llevar a cabo con la función para buscar un elemento. Se trata de realizar una compresión de caminos cada vez que ejecutemos esta operación. Como se observa en este código, tras buscar el rótulo del árbol donde se encuentra un elemento, procedemos a colgar ese elemento directamente del rótulo, es decir, del nodo raíz:
function buscar(rotulos=[], elemento=0){
//Buscar el rótulo del árbol que contiene el elemento
let rotulo = elemento;
while (rotulos[rotulo]!==rotulo){
rotulo = rotulos[rotulo];
}
//Compresión caminos
let i = elemento;
while (i!==rotulo){
[rotulos[i], i] = [rotulo, rotulos[i]];
}
return [rotulo, rotulos];
}Con esta mejora reducimos la altura en cada búsqueda, lo que minimizará el coste de las siguiente búsquedas. Para entenderlo mejor veamos paso a paso como al fusionar conjuntos y buscar un elemento se va reduciendo la altura. Tomemos un ejemplo simple con dos conjuntos disjuntos { 0, 1, 2 }, { 3, 4 }.
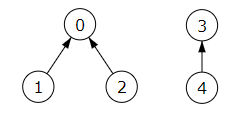
El array de rótulos es R = [0, 0, 0, 3, 3]. Ambos árboles tienen altura uno (ver Figura). Los rótulos son los valores 0 y 3. Buscar elementos que sean rótulos tiene coste unitario, pues esos valores coinciden con la posición en el array de rótulos, es decir, R[0] = 0 y R[3] = 3. Buscar cualquier otro elemento no tendrá un coste superior a 1, pues el primer while de la función buscar() no itera más de un nivel en el árbol. Recuerde que buscar un elemento supone obtener el rótulo del árbol. Se trata de ir obteniendo su padre de forma consecutiva hasta que lleguemos a uno que sea el raíz, lo que reconocemos cuando el valor coincide con el rótulo. Por ejemplo, buscar el elemento 2 necesita una iteración, puesto que hacemos R[2] = 0, siendo cero el rótulo dado que R[0] === 0.
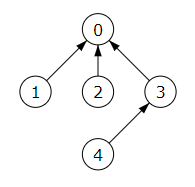
Ahora procedemos a fusionar ambos conjuntos con rótulos 0 y 3 con fusionar(rotulos, rangos, 0, 3), quedando como se observa en la Figura. El array de rótulos es R = [0, 0, 0, 0, 3]. Vemos que el árbol tiene una altura dos.
Buscar el elemento 4 en esta situación tiene un coste superior al tener esa rama una hoja más. Usando la función buscar(rotulos, 4) se producen dos iteraciones: R[4] = 3, R[3] = 0, siendo cero el rótulo dado que R[0] === 0.
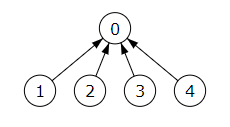
Pero con el segundo bucle while de la función buscar(), con el que realizamos la compresión de caminos, vemos que tras buscar el elemento 4 hace que lo cuelgue del raíz. Así quedará un árbol de altura uno optimizado para las siguientes búsquedas (Figura). El array de rótulos queda finalmente [0, 0, 0, 0, 0], con todos los elementos apuntando al rótulo cero.
La compresión de camino modifica la altura, pero sin embargo no es necesario actualizar el array de rangos. Dado que la compresión en ningún caso incrementará la altura, podemos considerar el array de rangos como una cota superior de alturas, sirviendo para su propósito para fusionar dos árboles. Por esa razón denominamos "rangos" en lugar de "alturas".
Con la implementación de las funciones para fusionar y buscar anteriores, el coste de ambas operaciones tiende a ser unitario tras utilizar repetidas veces las operaciones. Tal como se expone en el libro Fundamentos de Algoritmia de G.Brassard, P.Bratley, si hay n elementos, se producen b llamadas a buscar y f ≤ n-1 llamadas a fusionar, definiendo c = b+f, el coste asintótico de la partición es O(c × α(c, n)), donde α es la inversa de la función de Ackerman, que se denomina como función de crecimiento lento. A todos los efectos prácticos se demostró que α(c, n) ≤ 3, por lo que el coste es esencialmente lineal en c. Si además las llamadas a buscar no son superiores a n, el coste final es esencialmente lineal en n.
Por último vamos a comentar el código de una función accesoria para construir una estructura de partición. Si tenemos una estructura de conjuntos disjuntos como la siguiente:
{ 0, 1, 2 } { 3 } { 4, 5 } { 6 }podemos darle entrada a nuestra aplicación con arrays como sigue:
[[0,1,2],[3],[4,5],[6]]De esta forma le damos entrada en la siguiente función que nos construirá la partición devolviendo el array de rótulos, el de rangos y un array con los elementos:
function construir(conjuntos=[]){
let elementos = conjuntos.flat().sort();
let n = elementos.length;
let rotulos = [];
for (let conjunto of conjuntos){
let rotulo = Math.min(...conjunto);
for (let i=0; i<conjunto.length; i++){
rotulos[conjunto[i]] = rotulo;
}
}
let rangos = rotulos.map(v => 0);
return [rotulos, rangos, elementos];
}Planificación de tareas con plazo fijo: algoritmo rápido
Una de las aplicaciones de la estructura de partición que vimos antes es utilizarla para ejecutar la planificación de tareas con plazo fijo. Veamos el ejemplo interactivo:
Ejemplo: Planificación rápida con plazo fijo
planificar(tareas): Aclaración del orden de tareas seleccionadad con igual plazo
Con el ejemplo usando la entrada 7,3; 10,1; 20,3; 5,1; 15,1; 3,3 y el algoritmo lento obteníamos esta lista de tareas:
tareas[2] = {num: 5, beneficio: 15, plazo: 1}
tareas[1] = {num: 3, beneficio: 20, plazo: 3}
tareas[4] = {num: 1, beneficio: 7, plazo: 3}Mientras que con este algoritmo rápido y la misma entrada obtenemos:
tareas[2] = {num: 5, beneficio: 15, plazo: 1}
tareas[4] = {num: 1, beneficio: 7, plazo: 3}
tareas[1] = {num: 3, beneficio: 20, plazo: 3}El orden de las tareas en el primer caso eran los números 5, 3, 1 mientras que en el segundo es ahora 5, 1, 3. Esto sucede cuando hay dos tareas seleccionadas con el mismo plazo, pues a efectos de maximizar el beneficio da lo mismo ejecutarlas en cualquier orden. Lo importante es ver que de las seis tareas solo se seleccionan esas tres y se ordenan por plazo.
El código para implementarlo es el siguiente:
function planificarRapido(tareas=[{num: 0, beneficio: 0, plazo: 0}]){
tareas = tareas.sort((a,b) => b.beneficio-a.beneficio);
let plazos = [0, ...tareas.map(v => v.plazo)];
let n = tareas.length;
let plazoMax = Math.min(n, Math.max(...plazos));
let resultado = Array.from({length: plazoMax+1}, ()=>0);
let menores = Array.from({length: plazoMax+1}, (v,i)=>i);
let conjuntosIniciales = Array.from({length: plazoMax+1}, (v,i)=>[i]);
let [rotulos, rangos, elementos] = construir(conjuntosIniciales);
let numTareas = 0, rotulo, rotuloAnterior;
for (let i=1; i<=n; i++){
[rotulo, rotulos] = buscar(rotulos, Math.min(plazoMax, plazos[i]));
let menor = menores[rotulo];
if (menor>0){
resultado[menor] = i;
[rotuloAnterior, rotulos] = buscar(rotulos, menor-1);
menores[rotulo] = menores[rotuloAnterior];
[rotulos, rangos] = fusionar(rotulos, rangos, rotulo, rotuloAnterior);
}
if (numTareas >= plazoMax) break;
}
resultado = resultado.filter(v => v>0);
return resultado;
}Además de ordenar tareas y crear el array de plazos, obtenemos el plazo máximo que nos sirve para crear varios arrays: resultado, menores y conjuntos iniciales. Construimos la partición y pasamos a ejecutar el bucle voraz. Estudiemos paso a paso el problema 7,3; 10,1; 20,3; 5,1; 15,1; 3,3 para entender este algoritmo. Tras ordenar por beneficio decreciente nos queda esta lista inicial de tareas:
tareas = [
{num: 3, beneficio: 20, plazo: 3},
{num: 5, beneficio: 15, plazo: 1},
{num: 2, beneficio: 10, plazo: 1},
{num: 1, beneficio: 7, plazo: 3},
{num: 4, beneficio: 5, plazo: 1},
{num: 6, beneficio: 3, plazo: 3}
]Para entender el motivo de usar una estructura de partición para resolver este problema, intentemos resolverlo manualmente. Podríamos tener una estructura [[0], [1], [2], [3]] que contiene los plazos 0 hasta 3 instantes, cada uno a su vez en un array. El valor 3 es el máximo plazo y por tanto ninguna tarea podrá ejecutarse después de ese plazo. Iteramos por las tareas empezando en i=1. Si se selecciona pondremos ese índice i en una determinada posición de un array de resultado que inicialmente contiene ceros [0,0,0,0]. Vease el siguiente esquema:
i=0, inicio ⇒ [[0], [1], [2], [3]] ⇒ resultado = [0, 0, 0, 0] i=1, plazo=3, menor=3 ⇒ [[0], [1], [2, 3]] ⇒ resultado = [0, 0, 0, 1] i=2, plazo=1, menor=1 ⇒ [[0, 1], [2, 3]] ⇒ resultado = [0, 2, 0, 1] i=3, plazo=1, menor=0 ⇒ se desecha tarea i=4, plazo=3, menor=2 ⇒ [[0, 1, 2, 3]] ⇒ resultado = [0, 2, 4, 1]
Cuando analizamos la tarea i=1 cuyo plazo es 3 buscamos este valor que está en el array [3], siendo el menor de ese array el mismo valor 3. Como el menor es mayor que cero supone que hay un hueco para ejecutarla, con lo que selecionamos la tarea y la ponemos en la posición del menor 3 del array de resultado, quedando [0, 0, 0, 1]. Concatenamos el array [3] con el anterior array [2], quedando nuestro array de plazos de la forma [[0], [1], [2, 3]].
Si seguimos iterando este proceso comprobaremos que seleccionamos la tarea i=2, desechamos i=3 y seleccionamos i=4. Cuando tengamos tres tareas planificadas habremos acabado, pues las siguientes ya no tendrán hueco disponible. Quedará un array de resultados [0, 2, 4, 1]. El array de plazos se concatenará en un único conjunto [[0, 1, 2, 3]].
Esto que acabamos de hacer es tal como funciona una estructura de partición. Hay una función para buscar un elemento en un conjunto, una forma de obtener el menor de ese conjunto y otra para fusionar conjuntos (concatenar arrays). Veamos ahora este ejemplo paso a paso como se ejecuta en el ejemplo interactivo que utiliza estructura de partición.
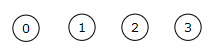
El array de plazos será [0,3,1,1,3,1,3]. En todos los arrays agregamos una posición cero adicional a modo de centinela, como hicimos en el primer apartado. Se observa que el plazo máximo es 3 y por lo tanto la planificación contendrá 3 tareas. Creamos el array de resultados [0,0,0,0]. Creamos la partición que nos devuelve el array de rótulos [0,1,2,3] y el de rangos [0,0,0,0]. La partición inicial se puede representar como 4 árboles que representan cada uno de los conjuntos disjuntos de altura cero, como se observa en la Figura.
También declaramos un array de menores [0,1,2,3], que en cada momento contendrá el elemento de menor valor en cada conjunto. Recordemos que en la operación fusionar anexamos el árbol de menor altura al de mayor altura, lo que puede ser que haga que el elemento de menor valor no sea necesariamente el rótulo del conjunto. Y para ejecutar la planificación necesitaremos el menor elemento en cada conjunto. En este ejemplo el menor siempre coincide con el rótulo, pero en otros casos puede que no sea así.
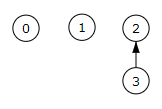
Empezamos el bucle voraz con la iteración i=1 que selecciona la primera tarea cuyo plazo es 3. Buscamos este valor entre los rótulos y nos devuelve el mismo valor, pues hasta ahora los árboles tienen altura cero. El menor es el mismo 3. El rótulo anterior es el 2. Fusionamos ambos conjuntos quedado tal como muestra la Figura. Agregamos la tarea i=1 al resultado en la posición del menor 3, con lo que la planificación hasta el momento es el Array de resultado [0, 0, 0, 1].
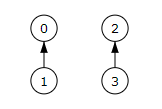
Pasamos a la tarea i=2 cuyo plazo es 1. Buscamos el rótulo del árbol donde se encuentra ese valor 1 y vemos que es el rótulo del árbol, con el menor el mismo valor 1. El rótulo anterior es el 0 y fusionamos ambos conjuntos quedando tal como muestra la Figura. Agregamos la tarea i=2 al resultado en la posición del menor 1 quedando la planificación [0, 2, 0, 1].
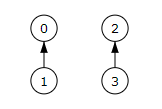
La siguiente tarea i=3 tiene un plazo 1 también. Buscamos ese valor 1 y obtenemos el rótulo 0. El menor de ese conjunto es también ese valor 0. Si se otiene un menor 0 se desecha la tarea. No hacemos nada más y la situación queda como antes (Figura).
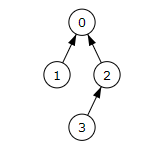
La siguiente es la tarea i=4, con plazo 3, valor que está en el árbol con rótulo 2, cuyo menor es el mismo valor 2. El rótulo anterior es el 0, fusionamos ambos conjuntos quedado como se observa en la Figura. Agregamos la tarea i=4 al resultado en la posición del menor 2 quedando la planificación [0, 2, 4, 1]. Ya tenemos tres tareas planificadas y ninguna de las siguientes podrá mejorar el beneficio total, así que salimos del bucle voraz.
Al finalizar se observa que el árbol resultante contiene todos los nodos. Hemos partido de 4 conjuntos disjuntos y los hemos fusionado en un único conjunto.
Con la planificación lenta del primer apartado analizamos el coste de las tareas en peor situación, cuando al ordenar decreciente por beneficio también se ordenan decreciente por plazo. Usamos como ejemplo 70,7; 60,6; 50,5; 40,4; 30,3; 20,2; 10,1. Obtuvimos un coste calculado T(n) = n2, con un coste de 49 iteraciones para estas tareas. Si lo ejecutamos con la estructura de partición se observará un coste de 18 iteraciones. Para ello disponemos un contador numIter++ al inicio de la función y al inicio del bucle voraz, tal como hicimos en el primer ejemplo. Y también ponemos ese contador dentro de los bucles while de la función buscar en la partición.
Se observa que el coste calculado es muy inferior. El coste asintótico es el máximo entre O(n log n) de la ordenación y O(n) esencialmente lineal de la partición, dado que no se realizan más de n búsquedas. Por lo que finalmente el coste es O(n log n), menor que O(n2) del algoritmo lento del primer apartado.