El coste de los recursivos
El coste de los algoritmos
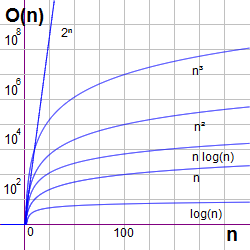
Los algoritmos recursivos van reduciendo el tamaño del problema en cada llamada. Si tenemos un problema de tamaño n puede que lleguemos a la solución con un coste linealmente proporcional a n y lo representamos como O(n), que leemos como "en el orden de n". Uno cuadrático sería O(n2) por lo que tendría un coste superior, al igual que uno exponencial como O(2n). En cambio uno con O(log n) tendría un coste inferior al lineal (entenderemos log como logaritmos en base 2).
En la Figura puede ver la representación de las funciones de coste más frecuentes: log(n), n, n log(n), n2, n3 y 2n.
Entender el coste de los recursivos sirve para buscar formas de plantearlos que supongan una reducción de ese coste. Por ejemplo, si un algoritmo tiene un coste que es de la forma f(n) y esa función está en el orden O(2n), significará que ese algoritmo tardará un tiempo T(n) = c×f(n), siendo c una constante que dependerá de la implementación donde se ejecute. Supongamos que en una implementación esa constante es c = 0.3 ms, que no parece mucho tiempo, pero si tenemos un problema de tamaño n = 50 resultará T(50) = 3×10-4 × 250 / (60×60×24×365) = 10710.615... años, !Tardaría más de 10710 años!
Por supuesto que el ordenador consumiría todos los recursos de memoria, pila de llamadas y ejecución muchísimo antes de finalizar. Veremos más abajo un ejemplo del recursivo de Fibonacci con coste también exponencial y que hemos limitado a n=26, pues con valores superiores llega a colapsar el navegador.
Sin embargo si f(n) estuviera en el orden O(n), que suele ponerse como f(n) ∈ O(n), entonces el algoritmo tomaría T(50) = 3×10-4 × 50 = 0.015 segundos, sólo 15 ms. Y si fuera f(n) ∈ O(log n) tardaría menos de 1.7 ms. La diferencia entre 10710 años y 1.7 milisegundos es más que importante para dedicarle un rato a estudiar el coste de los algoritmos y la forma de reducir dicho coste.
El factorial
En el tema anterior vimos el problema del factorial cuya recurrencia n! = n × (n-1)! y el caso base f(0) = 1 nos permitía plantear un recursivo para resolver el problema:
//Recursivo NO FINAL
function factorial(n){
if (n===0){
return 1;
} else {
return n*factorial(n-1);
}
}Escribiremos este recursivo separando el caso trivial del no trivial, indicando con un comentario //+1 el coste de las operaciones simples y con //+T(n-1) el coste de la nueva llamada al recursivo. Las que no cuenten como coste las indicamos con //+0. En este primer algoritmo separaremos el resultado a devolver, la la descomposición del problema, las llamadas y la combinación de soluciones parciales. Esto lo hacemos en este tema sólo para entender la estructura de un recursivo, pero en una aplicación finalizada podríamos evitar este exceso de instrucciones innecesarias y escribir el algoritmo de una forma compacta como el anterior.
function factorial(n){
numIter++;
let result; //+1
if (n===0){ //+1
//CASO TRIVIAL
result = 1; //+1
} else {
//CASO NO TRIVIAL
//descomponemos problema
let p = n-1; //+1
//llamadas
let s = factorial(p); //+T(n-1)
//combinamos soluciones parciales
result = n*s; //+1
}
return result; //+0
}En el código que se ejecuta también pondremos un contador de iteraciones numIter que indicará el coste del recursivo y que explicaremos más abajo. Pero este contador no forma parte del algoritmo finalizado y no le adjudicamos coste, sólo está para comprobar en estos ejemlos que el coste calculado coincide con este contador.
Ejemplo: Factorial
factorial(n): Iteraciones: Coste calculado T(n): El coste exacto o coste calculado del factorial recursivo anterior es T(n) = n+1. Es este un coste que se calcula para una implementación particular del algoritmo. En nuestro ejemplo lo vamos a obtener experimentalmente con el contador de interaciones y de forma teórica adjudicando unos costes unitarios a las operaciones.
Por otro lado y más importante es el coste asintótico. Para este factorial recursivo es T(n) ∈ O(n). Por ahora digamos que esto quiere decir que cualquier implementación particular de este recursivo no diferirá en el coste con la función f(n) = c1 n + c2 más allá de un par de constantes reales c1 y c2. Con O(n) estamos representando un conjunto de funciones que tienen la forma de un polinomio de grado uno y que suponen una cota superior del coste.
Para obtener costes empezamos siempre con la definición de la recurrencia que obtenemos del propio algoritmo. El caso trivial se limita a declarar la variable result (+1), calcular el comparativo (n===0) (+1) y asignarle un uno a la variable anterior (+1). La teoría dice que la suma de estos tres costes es el máximo de la instrucción con mayor coste. Así que Max(1, 1, 1) = 1.
Para n>0 tenemos también la declaración de la variable result (+1). el coste de la comparación (+1), descomponer el problema p=n-1 (+1), combinar la solución n×s (+1) y asignar el resultado (+1). Ahora también el coste combinado de estas instrucciones es uno. Por último hemos de sumar el coste de la nueva llamada ahora con tamaño n-1. No consideramos el coste de la devolución return. En el apartado siguiente ahondaremos más sobre esto.
Con el razonamiento anterior la definición de la recurrencia del coste será esta:
| T(n) = | { | 1 | si n=0 |
| T(n-1) + 1 | si n>0 |
Una forma de resolver esta recurrencia es desarrollarla desde n hasta el caso trivial n=0, donde sabemos por la definición que T(0) = 1, lo que nos permitirá resolverlo:
T(n) = T(n-1) + 1 = T(n-2) + 1 + 1 = ... = T(1)+∑(i=2..n) 1 = T(0)+∑(i=1..n) 1 = 1+nPor ejemplo, para n=6 tenemos:
T(6) = T(5)+1 = T(4)+2 = T(3)+3 = T(2)+4 = T(1)+5 = T(0)+6 = 1+6 = 7Observe que este coste coincide con el número de iteraciones en el ejemplo, valor que obtenemos incrementando el contador numIter en cada llamada.
Otra forma de resolver una recurrencia es intentar equipararla con la siguiente recurrencia genérica:
a0tn+a1tn-1+...+aktn-k = bnp(n)La parte de la izquierda es la llamada ecuación homogénea y la de la derecha es la ecuación particular, siendo p(n) un polinomio de cierto grado d≥0. Para resolverla se hace uso de la siguiente ecuación característica, donde el primer paréntesis resuelve la homogénea y el segundo la particular:
(a0xk+a1xk-1+...+a)(x-b)d+1 = 0Volvamos a nuestra recurrencia del factorial que podemos ponerla así:
T(n) - T(n-1) = 1Y donde identificaremos la parte homogénea y particular:
tn-tn-1 = 1n (n0)identificándose b=1 y p(n) = n0 un polinomio de grado cero, con lo que su ecuación característica es la siguiente, donde observamos que el término más pequeño tn-1 de la parte homogénea nos da el orden k=1 de la ecuación homogénea
(x1-x0)(x-1)0+1 = 0 ⇒ (x-1)(x-1) = 0 ⇒ (x-1)2 = 0Esta ecuación tiene por solución la raíz r=1 con multiplicidad 2, recordando que si r es una raíz con multiplicidad m, entonces rn, n rn, n2 rn, ..., nm-1 rn son todas soluciones de la recurrencia, siendo la solución general una combinación lineal de ellas:
tn = c1 1n + c2 n 1n = c1 + c2 nCon esto sería suficiente para saber que T(n) ∈ O(n) pues c1 y c2 son dos constantes que no modificarán el orden del coste. En cualquier caso para descubrir las constantes podemos dar las condiciones iniciales de dos valores cuyo coste conocemos o es fácil calcular: n=0 cuyo coste es 1 por definición y n=1 cuyo coste es 1 también, quedando entonces el coste T(1) = T(0)+1 = 1+1 = 2. Obtenemos las siguientes ecuaciones:
t0 = 1 ⇒ c1 + c2 0 = 1 t1 = 2 ⇒ c1 + c2 1 = 2de donde se deduce que c1 = 1 y c2 = 1 cumple lo anterior, con lo que la solución exacta es T(n) = n+1 y por tanto es correcto decir que T(n) ∈ O(n).
En general si tenemos un polinomio el coste asintótico es del término de mayor grado. Si fuera por ejemplo T(n) = 2n2 + 3n + 5 el coste sería O(n2).
Definir la recurrencia del coste
Lo que parece más díficil en el problema de analizar un algoritmo es establecer la definición de la recurrencia del coste. Para el factorial que vimos en el apartado anterior pusimos que T(0) = 1 para el caso trivial y T(n) = T(n-1) + 1 para el no trivial. Antes dijimos que si tenemos una secuencia de instrucciones el coste combinado es el de la instrucción de mayor coste. ¿Qué pasa si en lugar de eso decimos que el coste de una secuencia es la suma aritmética de los costes de cada instrucción? Pongamos aquí otra vez el código del recursivo del factorial que vimos en el apartado anterior:
function factorial(n){
let result; //+1
if (n===0){ //+1
result = 1; //+1
} else {
let p = n-1; //+1
let s = factorial(p); //+T(n-1)
result = n*s; //+1
}
return result; //+0
}Si sumamos costes, en el caso trivial tendriamos un coste 3 y en el no trivial 4 más el de la nueva llamada. Con esto la definición queda así:
| T(n) = | { | 3 | si n=0 |
| T(n-1) + 4 | si n>0 |
Las ecuaciones para obtener el coste ahora se plantean así:
a0tn+a1tn-1+...+aktn-k = bnp(n) (a0xk+a1xk-1+...+a)(x-b)d+1 = 0 tn-tn-1 = 1n (4 n0) (x1-x0)(x-1)0+1 = 0 ⇒ (x-1)(x-1) = 0 ⇒ (x-1)2 = 0Son las mismas ecuaciones que usamos en el apartado anterior, sólo cambia el dígito 4 cuando antes era un uno. Pero ese número no interviene en la obtención de la misma solución general:
tn = c1 1n + c2 n 1n = c1 + c2 nPor lo tanto no cambia el coste asintótico que sigue siendo O(n). Pero ahora si cambia la condición inicial T(0) = 3 y el primer valor T(1) = T(0) + 4 = 3+4 = 7
t0 = 3 ⇒ c1 + c2 0 = 3 t1 = 7 ⇒ c1 + c2 1 = 7Obteniendo c1 = 3 y c2 = 4 resultando el siguiente coste calculado:
T(n) = 4 n + 3En el caso del apartado anterior obtuvimos T(n) = n+1 y la diferencia con este coste calculado ahora está en la elección de las constantes c1 y c2. Esto quiere decir que cualesquiera otros valores particulares de estas constantes son una solución exacta válida. No debemos olvidar que el objeto de resolver las recurrencias es obtener el coste asintótico más que el coste calculado. Este último es una solución particular para una implementación concreta en una máquina determinada. Y la máquina más simple que podemos considerar es aquella en que suceden costes unitarios aplicando ciertas reglas, como que el coste de una secuencia es el de la instrucción de mayor coste. A continuación veremos esas reglas.
A las devoluciones return no les asignamos coste, pues suponemos que una función siempre devolverá algo: el valor que se devuelve o undefined cuando no se incluyen sentencias return. Hay que recordar que una función recibe y devuelve bien datos primitivos (string, number, boolean, symbol, null, undefined) o referencias a datos no primitivos. Estos nunca se pasan o devuelven por valor, sino más bien lo que se pasa o devuelve es el valor de la referencia al objeto. Así que supone el mismo coste recibir o devolver un número o una cadena que una referencia a un Array o cualquier otro objeto que no sea un dato primitivo. De igual forma ignoramos el coste de crear el contexto de la función y de la pila de llamadas, coste intrínseco a cada implementación.
El coste en el caso no trivial es el más importante, puesto afectará a la solución general y, por tanto, a la obtención del coste asintótico. El del caso trivial tiene generalmente un coste constante. En ese caso afectará sólo a la solución del coste calculado, pues de ahí se obtiene la resolución del sistema de ecuaciones que conducen a obtener la solución particular.
La mayoría de operaciones simples que afecten a tipos de datos primitivos (string, number, boolean, symbol), así como declaraciones y asignaciones a variables y ejecución de comparaciones les asignamos un coste unitario. Para una secuencia de instrucciones se toma como coste el de la instrucción que tenga mayor coste. Así que una secuencia de operaciones simples tiene un coste combinado unitario. Esto podemos entenderlo de otra forma: si en cada llamada al recursivo ejecutamos en el caso no trivial la misma cantidad de 6 operaciones, por ejemplo, 1 comparativo, 2 sumas y 3 restas, esto tomára un tiempo Ts = 1 en nuestro máquina simple. Pero en un ordenador real tardará ese tiempo multiplicado por una cierta constante k1×Ts. En otro tardará k2×Ts. En todos se ejecutan 6 operaciones en cada llamada y el coste sólo difiere en una constante multiplicativa con respecto al coste calculado en nuestra máquina simple.
En JavaScript el coste de sumar dos números es constante con respecto al tamaño de esos números. Esto es porque los números se almacenan en un registro de 64 bits con el formato IEEE754 sea cual sea ese número. Pero operaciones sobre cadenas del tipo string no siempre resultarán simples. Por ejemplo, str.toLowerCase() supone recorrer todos los caracteres de la cadena y convertirlos a minúsculas. Es una operación cuyo coste será proporcional al tamaño de la cadena. Y si ese tamaño forma parte del tamaño del problema no deberíamos considerarlo como una operación simple.
Veamos ahora el caso de los bucles con este recursivo:
function rec(array, n=array.length){
let result; //+1 (Ta)
if (n===0){ //+1 (Tb)
result = 1; //+1 (Tc)
} else {
let p = n-1; // +1 (Td)
for (let i=0; i<p; i++){ // +1 (Te)
array[i] = array[i+1]; //+1 (Tf)
array[i] += 1; //+1 (Tg)
}
let s = rec(array, n-1); //+(n-1) (Th)
result = s*2; //+1 (Ti)
}
return result; //+0 (Tj)
}En el caso no trivial tendremos que el coste es el máximo de los costes la secuencia de instrucciones Ta, Tb, Td, Te, Tf, Tg, Th, Ti, Tj. Ese máximo está condicionado por el bucle Te, Tf, Tg. El coste Te es el de cabecera del bucle. El coste del interior del bucle es Tfg = Máximo(Tf, Tg) = 1 pues se aplica la regla de la secuencia de instrucciones. Este coste, se ejecuta n-1 veces. Vease que cuando n=1 se ejecuta cero veces, pero aún así se ejecuta la cabecera del bucle. Así que el coste del bucle ahora si es la suma de la cabecera más su interior: Tefg = Te+Tfg×(n-1) = 1+1×(n-1) = n. Finalmente el coste en secuencia Máximo(Ta, Tb, Td, Tefg, Th, Ti, Tj) = n para n>0 pues estamos en el caso no trivial. A este coste de la secuencia de instrucciones le sumamos el de la nueva llamada llegando a la definición de la recurrencia T(n) = T(n-1) + n.
Si tenemos varios bucles en secuencia el coste es la suma de sus costes, pero teniendo en cuenta que el coste de las cabeceras está en secuencia mientras que sus interiores se suman, quedando entonces:
Máx(for1, for2, for3) + p + q + r = Máx(1, 1, 1)+p+q+r = 1+p+q+r
numIter++;
for (let i=0; i<p; i++){ //+1
numIter++;
// Una o más operaciones simples ⇒ +1
}
for (let i=0; i<q; i++){ //+1
numIter++;
// Una o más operaciones simples ⇒ +1
}
for (let i=0; i<r; i++){ //+1
numIter++;
// Una o más operaciones simples ⇒ +1
}
Observe que el primer contador numIter recoge el coste en secuencia de las tres cabeceras. Mientras que cada bucle tiene un contador para cada uno en su interior. No se modifica nada si hubiesen operaciones simples entre los bucles, dado que se acumulan a la secuencia de las cabeceras que registra el primer contador.
Si tenemos bucles anidados con tamaños p, q, r el coste sería (1+p)×(1+q)×(1+r). Vease que si alguno no se ejecuta, por ejemplo, r=0, aún así hemos de sumar un 1 por la cabecera. Si ignoramos las cabeceras tendríamos p×q×r, de tal forma que si r=0 tendríamos un coste cero para los tres bucles, lo que no es correcto pues se ejecutan los dos bucles exteriores p y q.
numIter++;
for (let i=0; i<p; i++){ //+1
numIter++;
for (let j=0; j<q; j++){ //+1
numIter++;
for (let k=0; k<r; k++){ //+1
numIter++;
// Una o más operaciones simples ⇒ +1
}
}
}Observe que antes de cada cabecera ponemos un contador. Y otro en el cuerpo del bucle más profundo. Tampoco se modifica nada si entre los bucles hubiesen operaciones simples, pues se suman en secuencia con los contadores de cabecera.
Coste de los tipos de datos no primitivos en JavaScript
Las operaciones que afecten a tipos de datos no primitivos requieren una especial atención. El Array no es un tipo de dato primitivo. Ahí podemos encontrar operaciones que podrían considerarse simples y otras que no. Declarar una variable que asigne un array vacío podría considerar simple: let arr = []. Aunque esta operación pueda ser más costosa que ejecutar una suma de dos números (que no sé si realmente lo es), sigue siendo simple pues si se ejecuta la misma en cada llamada, ese coste es constante con respecto al tamaño del problema en cada llamada.
De la misma forma podemos razonar con agregar un elemento con arr.push(123) o quitarlo con let x = arr.pop() también podrían ser simples. O usando la propiedad length del array con arr[arr.length] = 123 y let x = arr[arr.length-1] respectivamente. Tarden lo que tarden siempre será una constante con respecto al tamaño del problema.
Pero no podemos considerar simple agregar un elemento al principio con arr.unshift(123), pues esto requiere crear un nuevo elemento vacío al final, mover todos los contenidos un lugar a la derecha e insertar el nuevo valor al principio. Ni extraer eliminando el primer elemento con let x = arr.shift() pues requiere desplazar el resto de elementos a la izquierda.
Por lo tanto si el tamaño del array sobre el que se ejecuta una operación está determinado por el tamaño del problema del recursivo en cada llamada, no podremos ignorar ese coste. Como ejemplo veamos algunas más:
- Hacer una copia del Array con algo como
let nuevoArr = arr.map(v => v)o incluso con una sentencia tanto sencilla comolet nuevoArr = [...arr]. Supone iterar por el array para copiar todos los elementos, teniendo un coste igual al tamaño del array. - Métodos que eliminan elementos del Array como
arr.splice(i, j)que elimina j elementos a partir de la posición i. Si se elimina el mismo número de elementos en cada llamada, de tal forma que este número no está determinado por el tamaño del problema en cada llamada, podríamos considerar este coste unitario. En otro caso habría que considerar ese coste. - Comprobar si existe un valor con
if (arr.includes(x))tendrá un coste máximo de recorrer todo el array cuando el valor no exista o se encuentre el final del array. Si estamos buscando el coste asintótico O( ) consideraremos el caso de máximo coste.
En el siguiente ejemplo obtenemos valores de coste medidos directamente como tiempos de ejecución de algunos métodos de un Array.
Ejemplo: Coste métodos de Array
Este ejemplo mide el tiempo de ejecución de varios métodos sobre un Array con números desde el 1 al , repetiendo la ejecución veces por cada método para obtener tiempos apreciables. En cada repetición se crea un nuevo Array, pero el tiempo que se mide es exclusivamente el de ejecución de los métodos. La ejecución del ejemplo puede tomar varios segundos dependiendo del ordenador que se use.
| Método | Tiempo ms | Ejecución |
|---|---|---|
let x = array[n]; | Lee un elemento en el centro del array (Con n = Math.floor(array.length/2) | |
array.length--; array[array.length] = 0; | Quita un elemento al final y lo vuelve a poner al final. | |
array.push(array.pop()) | Quita un elemento al final y lo vuelve a poner al final. | |
array.unshift(array.shift()) | Quita un elemento al principio y lo vuelve a poner al principio. | |
let x = array.map(v => v) | Crea una copia del Array, no modificando el original. | |
let x = [...array] | Crea una copia del Array no modificando el original. | |
let x = array.slice(1) | Recorta el Array desde la segunda posición hasta el final devolviendo ese trozo en otro Array. No modifica el original. | |
let x = array.splice(0, 1); array.push(0) | Elimina una posición al inicio del Array, modificando el propio Array y devolviendo otro Array con los elementos eliminados. A continuación reponemos el tamaño del Array agregando un 0 al final. | |
let x = array.includes(1) | Devuelve verdadero pues el número 1 está en el Array (en la primera posición). | |
let x = array.includes(-1) | Devuelve falso pues el número -1 no está en el Array, debiendo recorrerlo completamente. |
En Chrome 77 con un Array de 100000 posiciones repitiendo la prueba 1000 veces se observa que la ejecución array.push(array.pop()) tiene coste de 1 ms o menos. De igual forma el método includes() cuando encuentra el valor al principio del Array tiene coste muy pequeño. Sin embargo si no existe el elemento buscará en todo el Array con un coste de unos 90 ms.
La ejecución de array.unshift(array.shift()) es más costosa con unos 55 ms. Recortar un Array supone 340 ms. Y crear un nuevo Array supone en torno a 380 ms con el operador de propagación y 1450 ms con el método map(). Eliminar una posición en el inicio tiene un coste de 14 ms.
Firefox 69 parece que optimiza los métodos unshift() y shift() pues su tiempo está por debajo del milisegundo, igual que el de push() y pop(). También optimiza splice(), pues esa ejecución tiene un coste por debajo de 1 ms. Sin embargo crear un nuevo Array tiene un coste muy superior con el operador de propagación (3500 ms), pero inferior con map() (800 ms). Buscar en un Array un valor que no existe tiene un coste ligeramente superior (120 ms).
¿Y qué hacer en estos casos de distinto comportamiento entre navegadores? Pues supongo que seguir la lógica y ponernos en el peor de los casos. Por ejemplo con el método unshift(): dado que un Array se puede ver como una lista apilada de valores, es "lógico" pensar que si tenemos una pila de cosas será más fácil la acción apilar otra cosa encima (push()) que al principio (unshift()), pues esto requiere quitar todo lo que hay encima, insertar y luego reponer la pila. Que al final resulta que alguna implementación optimiza esa operación, pues mejor porque ya nosotros nos hemos puesto en el peor de los casos.
Y si aún esto no nos convence podemos crear una versión de los métodos de Array para estudiar su coste. En el siguiente ejemplo puede ver los anteriores:
Ejemplo: Métodos de Array
let array = [10, 20, 30, 40, 50, 60];let x = La importancia de definir correctamente la recurrencia del coste
Ya vimos que es muy importante definir correctamente la recurrencia del coste. Si asignamos erróneamente los costes unitarios podemos llegar a un coste calculado incorrecto. Vamos a verlo en un ejemplo. Se trata de concatenar dos Array. De hecho el objeto Array tiene el método array1.concat(array2) para concatenar array2 a array1. Para implementarlo en JavaScript de una forma muy sencilla podemos usar un bucle que itere por array2 y vaya agregando los elementos a array1:
function concatBucle(array1, array2){
numIter++;
for (let i=0; i<array2.length; i++){
numIter++;
array1.push(array2[i]);
}
return array1;
}Esto tiene obviamente un coste lineal T(n) = n+1, sabiendo que la operación de agregar un elemento a un Array con push() tiene un coste unitario. Esta sería una forma muy simple de implementar la concatenación. Pero supongamos que por alguna extraña razón nos dicen que hemos de implementarlo con un recursivo:
function concatRecA(array1, array2){
numIter++;
if (array2.length>0){ // +1
//numIter += array2.length;
let k = array2.shift(); // +1 erróneamente
array1.push(k); // +1
concatRecA(array1, array2); // +T(n-1)
}
return array1;
}En este recursivo el caso trivial es cuando array2 está vacío, devolviéndose array1. En otro caso extraemos el primer elemento de array2 usando el método shift(), se lo agregamos al final a array1 y llamamos nuevamente al recursivo ahora con un elemento menos en array2.
Si ignoramos que el método shift() no tiene coste unitario, vemos que el coste en el caso trivial es el del comparativo +1, mientras que en el no trivial es ése coste en secuencia con shift() (erróneamente +1) y push() +1, resultando un coste final en secuencia unitario. Y esto sumado a la nueva llamada sobre array2 que ahora tiene un tamaño n-1. Así que la definición de la recurrencia del coste erróneamente planteada es la siguiente:
| T(n) = | { | 1 | si n=0 |
| T(n-1) + 1 | si n>0 |
Es idéntica al caso del factorial que vimos en el primer apartado de este tema, con un coste calculado T(n) = n + 1 siendo T(n) ∈ O(n). Resulta igual que el coste para el bucle. En cambio si consideramos acertadamente que el coste de array2.shift() no es unitario entonces la definición sería diferente. Por un lado el coste de array2.shift() con un tamaño n del Array supone iterar por los n elementos del Array y sumar la cabecera de ese bucle implícito, resultando un coste n+1. Entonces el máximo de la secuencia del comparativo +1, shift() +(n+1) y push() +1 es el máximo +(n+1):
| T(n) = | { | 1 | si n=0 |
| T(n-1) + n + 1 | si n>0 |
Resolvamos esta recurrencia usando el método de desarrollo. Se trata de empezar con T(n) = T(n-1) + n + 1 e ir resolviendo términos hasta que lleguemos al caso trivial:
T(n) = T(n-1) + n + 1 = = (T(n-2)+(n-1)+1) + n + 1 = T(n-2) + (n-1) + n + 2 = = (T(n-3)+(n-2)+1) + (n-1) + n + 2 = T(n-3) + (n-2) + (n-1) + n + 3 = = (T(n-4)+(n-3)+1) + (n-2) + (n-1) + n + 3 = T(n-4) + (n-3) + (n-2) + (n-1) + n + 4 = = ... = = T(1) + 2 + 3 + ... + (n-2) + (n-1) + n + (n-1) = = T(0) + 1 + 2 + 3 + ... + (n-2) + (n-1) + n + n = = 1 + ( ∑k=1..n k ) + n = = 1 + 1/2 (n2 + n) + nObserve que al desplegar hasta n-4 ya empezamos a deducir el siguiente término, por lo que pasamos directamente a los valores cercanos al caso trivial, caso que nos permite obtener el resultado, puesto que 1+2+...+n = ∑k=1..n k = 1/2 (n2 + n) es la suma de un progresión aritmética.
El coste ahora es cuadrático T(n) ∈ O(n2). En el ejemplo usaremos array2 con una longitud de 1000 elementos, por lo que el coste erróneo T(n) = n + 1 será 1001 mientras que T(n) = 1 + 1/2 (n2 + n) + n suponen 501501. El error cometido al despreciar el coste de shift() es muy importante. Si no detectamos este planteamiento erróneo estaremos usando un recursivo que no es muy eficiente.
Para hacerlo más eficiente hemos de evitar el uso de shift. Podemos arreglarlo pasando un tercer argumento n=array2.length que se inicia con la longitud de ese Array. El caso trivial será cuando n=0. En el no trivial obtenemos la posición simétrica por el inicio con p = array2.length-n, agregando a array1 el valor en esa posición. A continuación llamamos nuevamente reduciendo una unidad el tercer argumento. Este recursivo tiene un coste calculado T(n) = n + 1, dado que push() si tiene coste unitario:
function concatRecB(array1, array2, n=array2.length){
numIter++;
if (n>0){
let p = array2.length-n;
array1.push(array2[p]);
concatRecB(array1, array2, n-1);
}
return array1;
}En el ejemplo usaremos array2 con una longitud de 1000 posiciones, observando las iteraciones y el tiempo de ejecución de los métodos anteriores y también del método de JavaScript array1.concat(array2). Ejecutamos 5000 pruebas por cada método con objeto de obtener tiempos apreciables.
Ejemplo: Test concatenar arrays
| Método | Resultado | Iteraciones | Tiempo ms |
|---|---|---|---|
concatRecA(array1, array2) | |||
concatRecB(array1, array2) | |||
concatBucle(array1, array2) | |||
array1.concat(array2) |
En una ejecución en Chrome 78 obtengo 8 ms para el método de JavaScript array1.concat(array2), 31 ms para concatBucle(), 68 ms para concatRecB() y 376 ms para concatRecA(). Evidentemente este último es muy ineficiente. Por lo tanto hay que revisar bien la definición de la recurrencia del coste de tal forma que refleje la realidad de los costes unitarios.