Recursivos que reducen mediante substracción
Recursivos que reducen el tamaño mediante substracción
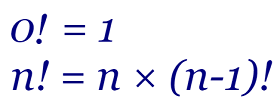
La función matemática factorial puede definirse de un forma iterativa con n! = ∏k=1..n k. También podemos definirla recursivamente con n! = n × (n-1)! y el caso base 0! = 1. En este caso decimos que el factorial de n es igual al producto de n por el factorial de n-1. En este paso realmente no estamos resolviendo nada, solo estamos reduciendo el tamaño del problema en una unidad, confiados en que cuando lleguemos al caso base obtengamos una solución. Y que cuando volvamos hacia atrás realizando las multiplicaciones obtengamos el resultado final.
El algoritmo del factorial que vimos en el tema anterior es simplemente una traducción a JavaScript de esa definición matemática recursiva:
function factorial(n){
if (n===0){
return 1;
} else {
return n*factorial(n-1);
}
}En este tema veremos varios ejemplos más de recursivos que reducen el tamaño del problema mediante substracción. En cada llamada se reduce en una cantidad fija, siempre la misma. Esto es diferente de otros recursivos que reducen el tamaño del problema mediante división y que veremos en un tema posterior. A éstos últimos se les denomina recursivos del tipo divide y vencerás, denominación que no debería aplicarse a los que reducen mediante substracción.
Invertir un Array
Tenemos una lista de valores a0, a1, ..., an-1 y queremos invertirla obteniendo an-1, an-2, ..., a0. Esta operación la vamos a realizar sobre la propia lista. Para la implementación usaremos el Array de JavaScript. De hecho este objeto dispone del método reverse() que intentaremos reproducir en el siguiente ejemplo usando un recursivo. Vease que ponemos el contador de iteraciones, obviando comentarios y exceso de instrucciones:
function reverse(array=[], i=0, j=array.length-1){
numIter++;
if (i>=j){
return array;
} else {
[array[i], array[j]] = [array[j], array[i]];
i++;
j--;
return reverse(array, i, j);
}
}La primera llamada será reverse(array) pasándose los parámetros por defecto para el primer índice i=0 y el último j=array.length-1. En cada llamada intercambiamos con destructuring un elemento al inicio con uno al final, incrementando el índice i y decrementando j. Acabaremos cuando i≥j. En el código anterior devolvemos el array, pero realmente no es necesario devolver nada puesto que el array se pasa por referencia, como todos los objetos que se pasen como argumentos en JavaScript. Pero para asimilarlo al método reverse() de JavaScript, devolveremos el propio Array, o mejor dicho, la referencia al mismo.
Ejemplo: Invertir un Array
reverse(array): Iteraciones: Coste calculado T(n): El tamaño del problema es n = j-i+1 en cada llamada. Con la primera llamada n = j-i+1 = (array.length-1)-0+1 = array.length que es el tamaño del array. En cada llamada quitamos dos elementos en el inicio y final del array, por lo que el tamaño se reduce en 2 unidades. El caso trivial sólo tiene el coste de la comparación, pues la devolución no supone coste. Las incluidas en el caso no trivial que intercambia posiciones y reduce el tamaño del problema es una secuencia con coste también unitario. Con esto la definición del coste queda como sigue:
| T(n) = | { | 1 | si n<2 (i≥j) |
| T(n-2) + 1 | si n≥2 (i<j) |
Vease que siendo n = j+i+1 podemos expresar el condicional del caso trivial como i ≥ j ⇒ 0 ≥ j-i ⇒ 1 ≥ j-i+1 ⇒ 1 ≥ n ⇒ n < 2. Y del no trivial como i < j ⇒ 0 < j-i ⇒ 1 < j-i+1 ⇒ 1 < n ⇒ n ≥ 2.
Aplicando el modelo de ecuación de recurrencia y característica:
a0tn+a1tn-1+...+aktn-k = bnp(n) (a0xk+a1xk-1+...+a)(x-b)d+1 = 0Identificamos nuestra recurrencia:
tn - tn-2 = 1n (n0)Siendo k=2, b=1, p(n) = n0, d=0 resulta esta ecuación característica:
(x2 - x0)(x-1)0+1 = 0 ⇒ (x2-1)(x-1) = 0con raíces r = 1, r=-1 de la parte x2-1 y r=1 de la otra parte x-1. Por lo tanto r=1 tiene multiplicidad 2:
tn = c1 1n + c2 n 1n + c3 (-1)n = c1 + c2 n + (-1)n c3Se deduce que T(n) ∈ O(n). Vemos que (-1)n=1 si n es par y -1 en caso impar. En cualquier caso podemos acumular c0 = c1+c3 con lo que la ecuación del coste queda tn = c2 n + c0. Veamos los primeros casos para obtener las condiciones iniciales y resolver las constantes:
T(0) = 1 T(1) = 1 T(2) = T(2-2) + 1 = T(0) + 1 = 2 T(3) = T(3-2) + 1 = T(1) + 1 = 2 T(4) = T(4-2) + 1 = T(2) + 1 = 3 T(5) = T(5-2) + 1 = T(3) + 1 = 3 T(6) = T(6-2) + 1 = T(4) + 1 = 4 T(7) = T(7-2) + 1 = T(5) + 1 = 4Se observa que se producen parejas de resultados iguales. Si empezamos con un tamaño n par tendremos la secuencia T(n), T(n-2), ..., T(6), T(4), T(2), T(0). Y si fuera impar tendríamos T(n), T(n-2), ..., T(7), T(5), T(3), T(1). Por lo tanto hay que tratar los casos por separado. Tomemos los dos primeros valores pares T(0) y T(2):
t0 = 1 ⇒ c0 = 1 t2 = 2 ⇒ 2 c2 + c0 = 2obtenemos c0 = 1, c2 = 1/2 que aplicamos a tn = c2 n + c0 obteniéndose para n par:
T(n) = n/2 + 1Con las dos primeras impares vemos que
t1 = 1 ⇒ c2 + c0 = 1 t3 = 2 ⇒ 3 c2 + c0 = 2resolviendo c0 = 1/2, c2 = 1/2 que aplicamos a tn = c2 n + c0 obtenemos para n impar:
T(n) = n/2 + 1/2Dado que si n ∈ ℕ es par sucede que n/2 + 1 = ⌊n/2⌋ + 1 y lo mismo pasa cuando n es impar n/2 + 1/2 = ⌊n/2⌋ + 1, con lo que podemos finalizar diciendo que:
T(n) = ⌊n/2⌋ + 1- ⌊x⌋ = floor(x): Redondea al entero inferior
- ⌈x⌉ = ceil(x): Redondea al entero superior
- [x] = round(x): Redondea al entero más cercano
Usamos este coste calculado en el ejemplo observándose que coincide con el contador de iteraciones numIter.
¿Podemos finalizar diciendo que T(n) ∈ O(n/2) y no al O(n)? Tendremos en cuenta que si tenemos dos funciones f(n) y g(n) podemos encontrar su relación con la siguiente regla del límite:
- Si limn→∞ f(n)/g(n) ∈ ℝ+ entonces f(n) ∈ O(g(n)) y g(n) ∈ O(f(n))
- Si limn→∞ f(n)/g(n) = 0 entonces f(n) ∈ O(g(n)) pero g(n) ∉ O(f(n))
- Si limn→∞ f(n)/g(n) = +∞ entonces f(n) ∉ O(g(n)) pero g(n) ∈ O(f(n))
Vemos que limn→∞ T(n)/g(n) = limn→∞ (n/2) / n = 1/2 ∈ ℝ+ con lo que T(n) ∈ O(n).
Otra forma de verlo es sabiendo que la definición T(n) ∈ O(f(n)) quiere decir que existe una constante c tal que T(n) ≤ c×f(n) y viendo que n/2 ≤ c× n se cumple con c=1/2.
Menor distancia entre dos puntos
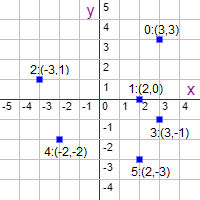
Tenemos un Array con puntos del plano [p0, p1, ..., pn-1] siendo cada punto pi = [xi, yi] también un Array. El problema es buscar dos puntos cuya distancia entre ellos sea la menor entre todas las posibles. Por ejemplo, en la Figura vemos que esos dos puntos son el 1 y el 3.
Una forma de resolverlo es tomar el último punto del Array, medir la distancia entre ese y el resto de puntos almacenanado la menor distancia. Cuando este bucle termine se llamará de nuevo al recursivo quitando ese último punto y se vuelve a hacer lo mismo. Llegamos a un tamaño 1 en cuyo caso devolvemos ∞.
En las subidas seleccionamos la menor distancia entre la calculada en el bucle y la que obtenemos de la llamada. Como hemos de devolver los puntos que se encuentren más cerca, usamos un Array [i, j, distancia] donde manejamos los índices i, j de dos puntos y la distancia entre ellos. En el caso trivial cuando tenemos uno o ningún punto devolvemos [-1, -1, ∞], pues no hay dos puntos ni distancia posible donde aplicar el concepto del problema.
function distancia(puntos=[], n=puntos.length){
numIter++;
if (n<2){
return [-1, -1, Infinity];
} else {
let [p, index, d] = [n-1, -1, Infinity];
let [x1, y1] = puntos[p];
for (let i=0; i<p; i++){
numIter++;
let [x2, y2] = puntos[i];
let dis = Math.sqrt((x1-x2)**2+(y1-y2)**2);
if (dis < d){
d = dis;
index = i;
}
}
let s = distancia(puntos, p);
if (s[2] < d){
return s;
} else {
return [p, index, d];
}
}
}En el ejemplo también damos la posibilidad de calcular la mayor distancia entre dos puntos, aunque no lo exponemos en el código para no entorpecer la lectura.
Ejemplo: Menor distancia entre dos puntos
Poner una lista de puntosx0,y0; x1,y1; ... separándolos con punto y coma. distancia(puntos): Detalle del resultado:Iteraciones: Coste calculado T(n): Vemos que en el caso trivial el coste es el del comparativo n<2 y el de construir el array [-1, -1, Infinity], ambas operaciones simples con coste unitario y cuya secuencia también es de coste unitario. El el caso no trivial tenemos el coste del comparativo y algunas instrucciones por fuera del bucle, incluida su cabecera, todas ellas operaciones simples en secuencia que tienen un coste unitario. Contabilizamos estos costes en secuencia con el contador numIter que hemos puesto a la entrada del recursivo.
En el interior del bucle ponemos otro contador, pues ahí tenemos otra secuencia de operaciones simples. El tamaño del bucle es n-1, por lo que el coste en el caso no trivial es T(n-1) + 1 + (n-1) = T(n-1) + n, quedando la siguiente definición de la recurrencia del coste:
| T(n) = | { | 1 | si n<2 |
| T(n-1) + n | si n≥2 |
Si desarrollamos la recurrencia con un tamaño de 6 elementos:
T(6) = T(5)+6 = T(4)+5+6 = T(3)+4+5+6 = T(2)+3+4+5+6 = T(1)+2+3+4+5+6Como T(1)=1 es el caso trivial, la solución T(6) = 1+2+3+4+5+6 = 21. Haremos un un desarrollo genérico:
T(n) = T(n-1)+n = T(n-2)+n+n = ... = T(1)+∑(i=2..n) i = ∑(i=1..n) i = ½ n2 + ½ nVemos que con esa fórmula se comprueba que T(6) = 21 tal como obtuvimos. Ya podíamos quedarnos aquí deduciéndose que T(n) ∈ O(n2), pues al ser un polinomio se toma el de mayor grado. Pero para seguir practicando apliquemos el método de solución con las ecuaciones de recurrencia:
a0tn+a1tn-1+...+aktn-k = bnp(n) (a0xk+a1xk-1+...+a)(x-b)d+1 = 0Identificándola con nuestra recurrencia:
tn - tn-1 = 1n (n1)Siendo k=1, b=1, p(n) = n1, d=1 resulta esta ecuación característica:
(x1 - x0)(x-1)1+1 = 0 ⇒ (x-1)3 = 0con raíz r = 1 con multiplicidad 3:
tn = c1 1n + c2 n 1n + c3 n2 1n = c1 + c2 n + c3 n2Con las condiciones iniciales y primeros valores T(1) = 1, T(2) = T(1)+2 = 3, T(3) = T(2)+3 = 6 planteamos el siguiente sistema de ecuaciones.
t1 = 1 ⇒ c1 + c2 + c3 = 1 t2 = 3 ⇒ c1 + 2 c2 + 4 c3 = 3 t3 = 6 ⇒ c1 + 3 c2 + 9 c3 = 6Resolvemos c1 = 0, c2 = 1/2, c3 = 1/2 con lo que la solución es la misma que obtuvimos con el desarrollo:
T(n) = ½ n2 + ½ nEn el algoritmo calculamos la distancia entre dos puntos con ((x1-x2)2+(y1-y2)2)1/2, pero podemos omitir la raíz cuadrada, dado que si a y b son dos distancias, cuando a<b entonces a2<b2 y lo mismo para el comparativo mayor que. Esto ahorra un coste de cómputo, pero sólo afectará a la constante multiplicativa manteniéndose el coste que hemos calculado.
Las torres de Hanoi
El problema de las torres de Hanoi se basa en que tenemos 3 postes y un número n de discos de diferentes radios en uno de los postes, de tal forma que están ordenados de mayor a menor. Tenemos que pasar esos discos a otro poste pero con la restricción de que en cada movimiento sólo podemos pasar un disco. Y que en ningún caso podrá haber un disco de mayor radio sobre otro menor, es decir, siempre tendrán que estar ordenados de forma decreciente.
En la Figura puede ver que se necesitan 7 movimientos para llevar los 3 discos que están en el poste de la izquierda al poste del centro. En todo momento se cumplen las restricciones que establecimos. Para implementar la solución usaremos un Array como poste, con los discos como números en orden decreciente. La evolución de los movimientos supondrán mover los números entre Arrays:
Movimiento Poste 1 Poste 2 Poste 3 ----------------------------------- 0 [3,2,1] [] [] 1 [3,2] [1] [] 2 [3] [1] [2] 3 [3] [] [2,1] 4 [] [3] [2,1] 5 [1] [3] [2] 6 [1] [3,2] [] 7 [] [3,2,1] []
El problema debemos resolverlo con 3 postes y n discos variable, para lo cual usamos la instrución let postes = [Array.from({length: n}, (v,i) => n-i), [], []]. Con esto construimos la estructura de datos que necesitaremos para hacer la primera llamada a hanoi(postes, 0, 1), siendo el segundo argumento el poste de la izquierda y el tercero el poste donde queremos trasladar los discos. Con 3 discos en el primer poste y optando por pasarlos al segundo, tendríamos la llamada inicial como hanoi([[3,2,1], [], []], 0, 1) y al final deberíamos obtener [[], [3,2,1], []], con los discos en el segundo poste.
En el algoritmo siguiente proveemos además un cuarto argumento que descubre el número de discos n de la longitud del poste i, que siempre será el primer poste. El argumento j es por defecto el segundo poste, aunque podemos configurarlo en el ejemplo. El caso trivial es cuando ya no quedan discos en el poste i-ésimo, aunque no hacemos nada ahí, dado que el movimiento de discos se produce entre dos llamadas al recursivo. En cada llamada reducimos el tamaño n y elegimos como poste el que queda libre entre i y j, lo que responde a la fórmula k = 3-i-j.
Con una llamada a hanoi(postes, i, j) estaremos moviendo un disco desde el poste i al poste j, para lo cual usamos los métodos pop() y push(). Para mover un disco de i hasta j, primero movemos los n-1 que están encima desde i al poste libre k para conservar el orden decreciente, movemos i a j usando los métodos pop() y push(), y finalmente hemos de reponer la situación moviendo los n-1 desde k hasta j.
Observe que el recursivo no devuelve nada, pues los movimientos se produce sobre el propio Array de entrada que en cada llamada se pasa por referencia.
function hanoi(postes, i=0, j=1, n=postes[i].length){
numIter++;
if (n===0) {
//caso trivial (traza)
} else {
let p = n-1;
let k = 3-i-j;
hanoi(postes, i, k, p);
postes[j].push(postes[i].pop());
hanoi(postes, k, j, p);
}
}En el ejemplo en ejecución ponemos una traza en el caso trivial, observándose como queda la situación en cada momento. Con 3 discos se necesitan 15 ejecuciones del recursivo, dato que obtenemos con un contador de iteraciones numIter que ponemos al inicio. En la ejecución 15 finalizaremos con los 3 discos en el poste seleccionado.
Ejemplo: Torres de Hanoi
hanoi([[3, 2, 1], [], []], 0, 1) = Iteraciones: Coste calculado T(n): Empecemos con la definición de la recurrencia. El caso trivial es cuando no hay ningún disco, con lo que el coste es el de la comparación n===0, operación simple que tiene coste unitario. Cuando el disco a mover tiene otros discos encima, primero tenemos que moverlos a un poste provisional con coste T(n-1), cambiar el disco a mover usando los métodos push() y pop() y volver a trasladar aquellos encima de ese disco con el mismo coste T(n-1). La comparación, descomposición del problema y el coste de los métodos push() y pop() son operaciones simples, con lo que el coste de esta secuencia es uno. Esto supone 2 T(n-1) + 1, quedando la definición como sigue:
| T(n) = | { | 1 | si n=0 |
| 2 T(n-1) + 1 | si n>0 |
Expresamos la recurrencia T(n) = 2 T(n-1) + 1 así:
tn - 2tn-1 = 1Y ahora la identificaremos con la recurrencia modelo y su ecuación característica:
a0tn+a1tn-1+...+aktn-k = bnp(n) (a0xk+a1xk-1+...+a)(x-b)d+1 = 0Identificando:
tn - 2tn-1 = 1n (n0)Siendo k=1, b=1, p(n) = n0, d=0 resulta esta ecuación característica:
(x1-2x0)(x-1)0+1 = 0 ⇒ (x-2)(x-1) = 0Las raíces son r=2 y r=1, ambas con multiplicidad 1, combinándose en esta solución general:
tn = c1 2n + c2 1n = c1 2n + c2Podemos ver ya que T(n) ∈ O(2n)
Resolvamos la solución exacta viendo que el caso trivial t0 = 1 por definición mientras que t1 = 2 t0 + 1 = 3, dando lugar a estas dos ecuaciones:
t0 = 1 ⇒ c1 20 + c2 = 0 ⇒ c1 + c2 = 1 t1 = 3 ⇒ c1 21 + c2 = 1 ⇒ 2c1 + c2 = 3Resolviendo c1=2, c2=-1 quedando el coste exacto como sigue:
T(n) = 2×2n - 1 = 2n+1 - 1Usamos este coste calculado en el ejemplo comprobándose que coincide con el contador de iteraciones numIter. Además se corrobora que T(n) ∈ O(2n) tras probar la primera de estas reglas:
- Si limn→∞ f(n)/g(n) ∈ ℝ+ entonces f(n) ∈ O(g(n)) y g(n) ∈ O(f(n))
- Si limn→∞ f(n)/g(n) = 0 entonces f(n) ∈ O(g(n)) pero g(n) ∉ O(f(n))
- Si limn→∞ f(n)/g(n) = +∞ entonces f(n) ∉ O(g(n)) pero g(n) ∈ O(f(n))
Vemos que limn→∞ T(n)/g(n) = limn→∞ (2n+1 - 1) / 2n = 2 ∈ ℝ+ con lo que T(n) ∈ O(2n).
Desordenar reversiblemente una cadena de caracteres
Hemos de desordenar una cadena de caracteres siguiendo un esquema reversible. Para ello podemos idear un algoritmo desordenar(chars) que intercambie los caracteres de una forma que podamos revertir ese intercambio con otro algoritmo simétrico revertir(chars). Supongamos que el que desordena es el siguiente:
function desordenar(chars=[]){
numIter++;
let n = chars.length;
if (n>=2) {
numIter += n;
let a = chars.shift(); // 1
let z = chars.pop(); // 2
desordenar(chars);
chars.push(a); // 3
chars.push(z); // 4
numIter += n;
a = chars.shift(); // 5
z = chars.pop(); // 6
desordenar(chars);
numIter += n-2;
chars.unshift(z); // 7
numIter += n-1;
chars.unshift(a); // 8
}
}Quitamos dos caracteres con shift() y pop(), uno al principio y otro al final. LLamamanos nuevamente a desordenar hasta que queden menos de dos elementos. En la subida ponemos esos dos elementos al final con push(). A continuación repetimos el proceso pero en la nueva subida los ponemos al pincipio con unshift(). Si hacemos desordenar("abcde") obtenemos "cebad". Ahora si revertimos el proceso con revertir("cebad") obtenemos la cadena original "abcde".
El código de revertir() es el siguiente, donde no incluimos contador de iteraciones, pues no resulta exactamente el mismo valor que el anterior, aunque no será muy diferente. Se observa que las extracciones e inserciones de elementos son simétricas con respecto al algoritmo desordenar(), lo que puede comprobar con los comentarios con números del 1 al 8, intercambiando shift/unshift y pop/push.
function revertir(chars=[]){
let n = chars.length;
if (n>=2) {
let a = chars.shift(); // 8
let z = chars.shift(); // 7
revertir(chars);
chars.push(z); // 6
chars.unshift(a); // 5
a = chars.pop(); // 4
z = chars.pop(); // 3
revertir(chars);
chars.push(a); // 2
chars.unshift(z); // 1
}
}En el ejemplo puede usar el botón con "⇑" para insertar el valor obtenido en el campo de texto. Ejecutaremos primero desordenar, trasladaremos la cadena desordenada al campo de texto y luego aplicaremos revertir para obtener la cadena original. Con el botón "···" reponemos el valor inicial del campo de texto por si quiere repetir la operación.
Ejemplo: Desordenar reversible
desordenar() = n: Iteraciones: Coste calculado T(n): Vamos a calcular el coste del recursivo desordenar(). No haremos nada sobre revertir() para no recargar mucho este tema. Ese coste puede ser ligeramente diferente, aunque serán del mismo orden de coste. Para el caso trivial de desordenar() tenemos el coste de la declaración y asignación de entrada y del comparativo, ambos con coste combinado unitario. Veáse que el caso trivial es n<2, donde no es necesario ejecutar nada.
Para el caso no trivial recordemos que push() y pop() tienen coste unitario, mientras que shift() y unshift() tiene coste el tamaño del array que se esté manejando. Así que tenemos el coste unitario de la entrada del algoritmo, más n para el primer shift() pues en ese momento chars tiene ese tamaño, más otro n del siguiente shift() dado que hemos repuesto con push() los dos elementos tras la primera llamada, más n-2 del primer unshift() pues al volver de la segunda llamada el Array tiene también dos elementos menos, y más n-1 del último unshift() pues acabamos de insertarle uno.
En resumen 1+n+n+(n-2)+(n-1) = 4n-2, con lo que la definición de la recurrencia queda así:
| T(n) = | { | 1 | si n<2 |
| 2 T(n-2) + 4n - 2 | si n≥2 |
Expresamos la recurrencia T(n) = 2 T(n-2) + 4n - 2 así:
tn - 2tn-2 = 4n - 2Y ahora la identificaremos con la recurrencia modelo y su ecuación característica:
a0tn+a1tn-1+...+aktn-k = bnp(n) (a0xk+a1xk-1+...+a)(x-b)d+1 = 0Identificando:
tn - 2tn-2 = 1n (4n1 - 2)Siendo k=1, b=2, p(n) = 4n1 - 2, d=1 resulta esta ecuación característica:
(x2-2x0)(x-1)1+1 = 0 ⇒ (x2-2)(x-1)2 = 0Las raíces son r=+2½, r=-2½ y r=1 de multiplicidad 2, combinándose en esta solución general:
tn = c1 2n/2 - c2 2n/2 + c3 1n + c4 n 1n= c1 2n/2 - c2 2n/2 + c3 + c4 nPodemos ver ya que T(n) ∈ O(2n/2). Para simplificar el cálculo del coste exacto agruparemos las dos primeras constantes en una, pues al fin y al cabo son constantes a calcular y no variables:
tn = (c1 - c2) 2n/2 + c3 + c4 n = c0 2n/2 + c4 n + c3Ahora es importante darse cuenta que si empezamos con n impar sólo pasaremos por valores impares. Cuando n = 2k+1 (impar) tendremos T(2k+1) = 2 T(2k+1-2) + 4(2k+1) - 2 = 2 T(2k-1) + 8k - 2 observándose que T(2k-1) es también un coste sobre un tamaño impar 2k-1. Y lo mismo para pares T(2k) = 2 T(2k-2) + 4(2k) - 2 = 2 T(2(k-1)) + 8k -2 siendo 2(k-1) también un par.
En estos casos es mejor separar la solución en dos partes, pares e impares. Calculemos los primeros valores de la recurrencia:
T(0) = 1 T(1) = 1 T(2) = 2 T(2-2) + 4×2 - 2 = 2 T(0) + 6 = 8 T(3) = 2 T(3-2) + 4×3 - 2 = 2 T(1) + 10 = 12 T(4) = 2 T(4-2) + 4×4 - 2 = 2 T(2) + 14 = 30 T(5) = 2 T(5-2) + 4×5 - 2 = 2 T(3) + 18 = 42Aplicamos la solución general con los valores pares n=0, 2, 4.
t0 = 1 ⇒ c0 20/2 + c3 = 1 t2 = 8 ⇒ c0 22/2 + 2 c4 + c3 = 8 t4 = 30 ⇒ c0 24/2 + 4 c4 + c3 = 30Se obtiene c0=15, c4=-4 y c3=-14 quedando el siguiene coste calculado para n par:
T(n) = 15×2n/2 - 4 n - 14Para impares n=1, 3, 5 se plantean las siguientes ecuaciones:
t1 = 1 ⇒ c0 21/2 + c4 + c3 = 1 t3 = 12 ⇒ c0 23/2 + 3 c4 + c3 = 12 t5 = 42 ⇒ c0 25/2 + 5 c4 + c3 = 42Se obtiene c0=19×2-1/2, c4=-4 y c3=-14 quedando el siguiene coste calculado para n impar:
T(n) = 19×2-1/2×2n/2 - 4 n - 14Dado que si n ∈ ℕ es par sucede que n/2 = ⌊n/2⌋ y cuando n es impar n/2 = ⌊n/2⌋ + 1/2, con lo que podemos finalizar diciendo que:
- Con n par: T(n) = 15×2n/2 - 4 n - 14 = 15×2⌊n/2⌋ - 4 n - 14
- Con n impar: T(n) = 19×2-1/2×2⌊n/2⌋ + 1/2 - 4n - 14 = 19×2⌊n/2⌋ - 4 n - 14
Podemos agrupar ambos resultados:
T(n) = (17-2(-1)n) 2⌊n/2⌋ - 4 n - 14Usamos esta fórmula en el ejemplo observándose que su resultado coincide con el contador numIter. Por otro lado es evidente que T(n) ∈ O(2⌊n/2⌋) dado que aplicando la regla del límite que ya hemos visto en un apartado anterior limn→∞ T(n)/2n/2 ∈ ℝ+ pues resulta o bien 15 cuando n es par o bien 19 cuando es impar.
Coste de recursivos que reducen el problema mediante substracción
Recopilamos a continuación los ejemplos de los recursivos de este tema:
| Recursivo | Recurrencia | Coste exacto | Coste asintótico |
|---|---|---|---|
| Factorial | T(0) = 1, T(n) = T(n-1)+1 | n+1 | O(n) |
| Reverse | T(0) = 1, T(1) = 1, T(n) = T(n-2)+1 | ⌊n/2⌋+1 | O(n) |
| Distancia | T(0) = 1, T(1) = 1, T(n) = T(n-1)+n | ½(n2+n) | O(n2) |
| Hanoi | T(0) = 1, T(n) = 2 T(n-1)+1 | 2n+1-1 | O(2n) |
| Desordenar | T(0) = 1, T(1) = 1, T(n) = 2 T(n-2)+4n-2 | (17-2(-1)n)2⌊n/2⌋-4n-14 | O(2⌊n/2⌋) |
Todos ellos tienen algo en común: reducen el problema mediante substracción. En algunos casos se produce una llamada y en otras dos. Se observa que los que realizan dos llamadas tiene un orden exponencial. Hay un método para obtener el orden del coste directamente desde la definición de la recurrencia:
Si T(n) = a T(n-b) + p(nk) con a≥1, b≥1 y p(nk) un polinomio de grado k≥0 el orden del coste puede deducirse directamente:
| T(n) ∈ | { | O(nk+1) | si a=1 |
| O(a⌊n/b⌋) | si a>1 |
Pero aún pueden darse recursivos que reducen también mediante substracción y no pueden encuadrarse en los anteriores. Veremos un par de ellos en los temas siguientes:
- Fibonacci, que responde a la recurrencia f(n) = f(n-1) + f(n-2), por lo que en una primera implementación daría lugar a una definición del coste similar a esa función que no se adapta al modelo de substracción anterior.
- Permutar, pues dado que en principio hay n! permutaciones de un conjunto de n elementos, el coste también irá ligado a n!, tampoco adaptándose a ese modelo.